基于样本特征解码约束的GANs

陈泓佑 陈 帆 和红杰 朱翌明

生成式对抗网络(Generative adversarial networks,GANs)是2014 年 Goodfellow 等[1]依据零和博弈思想和纳什均衡原理提出的一种数据生成模型,被广泛应用于图像生成领域.GANs 在网络结构上主要由生成器G网络和判别器D网络组成[1-3].G网络的目的是将随机噪声映射到训练集分布中,对随机噪声和训练数据的联合概率密度进行建模,关注于数据生成过程.D网络的目的是区分出馈入样本的类别问题,关注于生成数据和训练数据的最优分界面.GANs 的最大特点是对抗学习方式,训练过程中G网络和D网络交替对抗训练,两者的能力同步提升.

由于GANs 在图像数据生成上的出色表现,此后为提高GANs 生成图像的多样性(模式坍塌问题)和质量等,研究者提出了许多GANs 衍生模型.

从加入条件变量和图像隐码控制方面进行改进.Mirza 等[4]提出的条件生成式对抗网络尝试利用训练集样本的某些信息(如图像类别标签)来提高随机噪声z的可解释性,使得生成图像质量有所提高.Odena[5]提出的半监督学习生成式对抗网络将GANs 进行拓展,利用半监督学习使得D网络分类能力提高,能够有效提高生成图像质量及收敛速度.Odena 等[6]提出的辅助分类器生成式对抗网络可实现多分类问题,输出的则是对应标签的概率值,有效提高了GANs 模型模拟多类别、高分辨率数据集的效果.Chen 等[7]提出的信息极大化生成式对抗网络在GANs 对抗学习的基础上,通过引入一个训练集样本对应的隐含信息(如类别标签,倾斜度),使得隐含信息与生成样本具有较高的互信息,有效提高图像生成质量.Donahue 等[8]提出双向生成式对抗网络 (Bidirectional generative adversarial networks,BiGANs)是一种双向结构的对抗模型,增加了一个训练好的编码器E 网络用于提取训练样本隐码c,在D网络的馈入信息是随机噪声z与对应生成样本配对或样本隐码c与对应的训练样本配对,在生成实际场景图像上能取得很好的效果.以上GANs 中对于需要标签信息的GANs 模型限制了其在无监督对抗学习中的应用.双向生成式对抗网络中隐码的引入使得训练样本反复被编码器编码,而且馈入到D网络的数据不仅仅是图像样本,还有隐码c,整个GANs 网络框架变得更复杂,增加训练代价.

从GANs 网络结构或框架设计方面进行改进.Radford 等[9]提出的深度卷积生成式对抗网络(Deep convolutional generative adversarial networks,DCGANs)使用重新设计的卷积神经网络作为G和D网络,能够有效提高图像生成质量,并且成为GANs 网络结构设计上的标准模型之一.Denton等[10]提出的一种拉普拉斯金字塔生成式对抗网络模型,结合GANs 和条件GANs 的一些优点,使用多个GANs 逐层地生成高质量自然图像.Brock等[11]基于残差网络设计的大型生成式对抗网络能有效生成大尺寸,高质量的自然图像,但参数量明显大于一般GANs 模型,需要更多的硬件资源和时间成本.Nguyen 等[12]提出的双判别器生成式对抗网络使用两个D网络更细化GANs 中D网络的分类任务,能使得训练收敛速度变快及提高生成图像的多样性.张龙等[13]提出一种协作式结构的GANs模型提高生成图像质量,一定程度避免了模式坍塌现象的发生.GANs 网络结构的设计通常难度较大,这也是到目前为止,通过结构设计提升GANs 能力的经典GANs 模型很少的主要原因.

从优化目标函数梯度消失方面进行改进.GANs优化Jensen-Shannon (JS)散度时可能导致梯度消失,使得训练效果相对较差,多样性不足[14].研究者主要是使用其他散度代替JS 散度.Arjovsky 等[14]提出沃瑟斯坦距离生成式对抗网络,利用沃瑟斯坦距离来描述作为两个分布的相似度;这有效避免了优化JS 散度容易出现的梯度消失现象,但对D网络权重剪枝比较粗暴.Mao 等[15]提出的最小二乘生成式对抗网络(Least squares generative adversarial networks,Least squares GANs 或LSGANs)是利用最小二乘原理,将G和D网络的损失函数设计成最小二乘形式,使得GANs 优化生成数据分布和训练数据分布的Pearson 散度,避免梯度消失,并且损失函数收敛过程更平稳.Berthelot 等[16]提出的边界平衡生成式对抗网络(Boundary equilibrium generative adversarial networks,BEGANs)将一个自编码器作为D网络,设计了G和D网络的平衡度量方法来优化沃瑟斯坦距离,进而引入新的超参数来平衡两个网络训练,以期得到更好的生成图像.Gulrajani 等[17]提出的梯度惩罚沃瑟斯坦距离生成式对抗网络(WGANs with gradient penalty,WGANsGP),Wu 等[18]提出的沃瑟斯坦散度生成式对抗网络均是WGANs的改进模型,其中WGANsGP 通过梯度惩罚的方式替换掉权重剪切,从而避免因权重剪切导致的权重集中化和调参上的梯度消失问题.沃瑟斯坦散度生成式对抗网络通过引入沃瑟斯坦散度,从而去除WGANs中D网络的Lipschitz 条件,又能保留沃瑟斯坦距离度量两个分布的良好性质(如JS 散度的梯度消失问题).Su[19]提出的对偶GANs 模型,通过引入合理的概率散度并找出它的对偶表达,再将其转化成极小-极大博弈形式,从而避免了类似于WGANs 需要的Lipschitz 条件和多数GANs 容易发生梯度消失问题.Zhao 等[20]提出基于能量的生成式对抗网络是将D网络看成能量函数,提供了一种基于能量解释的GANs,并且通过pull-away term 策略来防止梯度消失问题导致的模式坍塌.王功明等[21]等提出一种基于重构误差能量函数的GANs 模型,利用深度置信网络作为G网络,能预防网络梯度消失,在生成效果和网络学习效率上有所提升.这些方法虽然能有效解决梯度消失问题,但普遍需要比较多的迭代次数,特别是优化沃瑟斯坦距离的GANs,通常为使得D网络满足1-Lipschitz 条件,每个批次的训练中很可能需要对其进行多次训练.

除此之外还有其他的改进途径.Qi[22]提出的损失敏感型生成式对抗网络主要为了限制GANs 试图模拟任意训练集分布的能力,让生成模型能够更偏向于改进真实度不高的样本从而提高图像生成效果.Zhang 等[23]提出的自注意力生成式对抗网络(Self-attention generation adversarial networks,SAGANs),利用注意力机制嵌入G网络和D网络中,使得两个网络能更好地学习网络自发关注的训练图像特征提高了生成图像质量和多样性,但其网络规模和训练迭代次数有所增加.

考虑到优化JS 散度容易带来的梯度消失问题,无监督GANs 模型在训练上更便利的优点.本文依然将JS 散度作为主优化目标的前提下,提出了一种基于训练集样本特征解码损失约束的无监督GANs模型.所设计的模型不仅尽量避免优化JS散度可能带来的梯度消失问题,同时也通过改进GANs 网络拓扑结构,融入样本本身的特征信息进行训练以提高GANs 图像生成能力.首先利用无监督特征学习模型预训练出训练集样本的中间层特征;然后构建一个与G网络结构一致和权重共享的解码器Dec,在每次对抗训练前使用本文设计的约束条件进行图像特征解码;最后再进行优化JS 散度的GANs 对抗学习.为验证所设计的GANs 性能,利用Celeba和Cifar10 数据集,对比分析了几种典型GANs 模型的生成效果.实验结果表明,本文方法能有效提高生成图像的多样性和质量的同时,还能减少训练所需的epoch 数.

1 对抗原理

GANs 的典型结构由一个生成器G和判别器D组成.G网络的任务是模拟训练集X进行数据生成,D网络的任务是分辨出馈入的样本属于X或者G(Z).

G网络的每个输入量为一个随机噪声z,z ∈Z且Z～FZ(z),随机噪声z的分布函数FZ(z)通常为正态分布或均匀分布.记训练样本x,x ∈X且X～FX(x),其中FX(x) 为训练样本集X的分布函数.那么D和G网络的损失函数分别为:

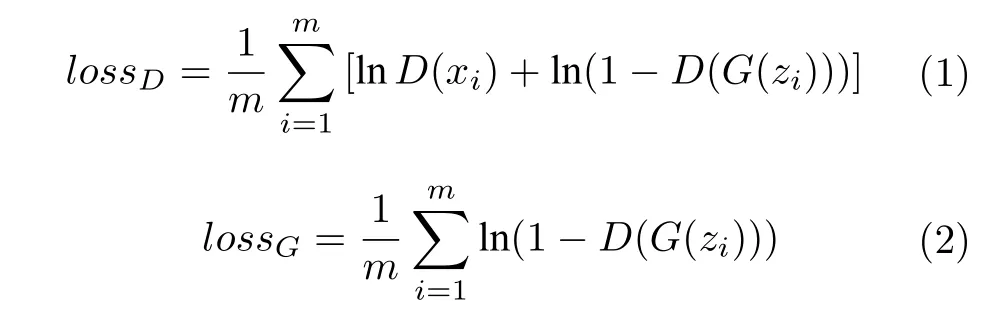
式中,m是每次馈入神经网络样本的个数.从而整个网络的博弈损失函数为:

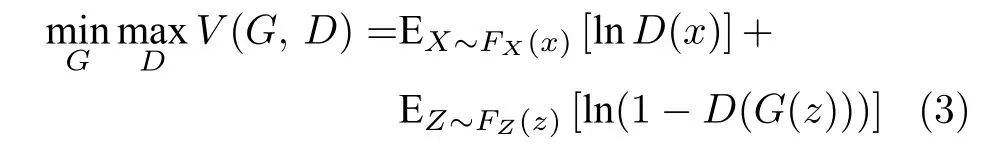
式中,V(G,D)是一个二元极小极大零和博弈函数,E(·) 为 期望函数.优化损失函数最终目的为使得G(Z)的统计分布FG(x) 趋近于训练样本集X的分布FX(x).为便于以下讨论,使用概率密度函数代替分布函数来描述分布.

2 解码约束的GANs

本节先分析优化JS 散度可能带来的梯度消失问题;然后提出了本文解决方法,同时给出了理论推导,为本文的解决方法提供依据;最后给出本文方法的训练步骤.

2.1 问题分析

为便于分析和讨论,先引入Kullback-Leibler(KL)散度和JS 散度的定义.

定义1[24].设两个具有相同样本空间 Ω 的随机变量X和G的概率密度函数分别为fX(x)和fG(x).KL 散度定义为:

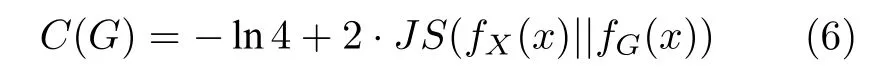
式(6)表明,式(3)的优化目标其实是最小化训练集X的概率密度函数fX(x) 和生成集G(Z)的概率密度函数fG(x)的JS 散度.

Arjovsky 等[14]在WGANs 的分析过程中指出当生成样本集分布fG(x) 与训练样本集分布fX(x)的相似度越低,即当两个分布的交叉区域越小,JS(fX(x)||fG(x))越接近于常数1.这可能引发损失函数梯度消失的现象.在GANs 训练过程中,fG(x)是逐渐拟合fX(x)的过程,JS 散度的固有性质可知,在GANs 训练的起步阶段梯度消失现象更明显.即使GANs 能够继续通过优化方法进行参数更新,为使得fG(x) 与fX(x)有足够的相交区域,也需要更多epoch 数进行训练.解决这个问题的一般方法是使用Pearson 散度或沃瑟斯坦距离代替JS 散度重新设计损失函数.

2.2 特征解码约束的GANs

由第2.1 节分析可知,JS 散度为常数而导致梯度消失的一个重要前提是fG(x) 与fX(x)的相似度足够低.那么通过添加约束条件利于fG(x)相 似于fX(x)可以达到尽量避免JS 散度为常数的目的,为此本文设计了一种JS +λ·KL 混合散度的约束方法.约束条件KL(fX(x)||fG(x)) 的目的是为使得fG(x)与fX(x)的相交区域变大.

如图1 所示,本文设计的GANs 分为3 个部分: 1)特征学习部分: 目的是预训练出训练集X的特征集C.2)解码学习部分: 目的是先通过本文设计的解码约束条件对特征集C进行解码,完成KL(fX(x)||fDec(x))约束.又通过解码器Dec与G网络结构一致,参数共享,以近似达到KL(fX(x)||fG(x)) 约束.最终使得在优化JS 散度前fG(x)与fX(x)相交区域变大,JS 散度不易为常数,从而尽量避免出现梯度消失现象.3)对抗学习部分: 通过优化JS 散度使得fG(x) 模拟fX(x).其中特征学习部分是预训练,解码学习和对抗学习部分需要一起动态学习.与一般含自动编码机GANs 不同的是,本文自动编码机主要目的是预训练出可用的隐含特征.例如,与双向生成式对抗网络相比,隐含特征c不会馈入D网络对其参数更新及直接参与对抗训练,仅用于解码学习;与BEGANs 相比,D网络的任务仍然是二分类,无编码功能.

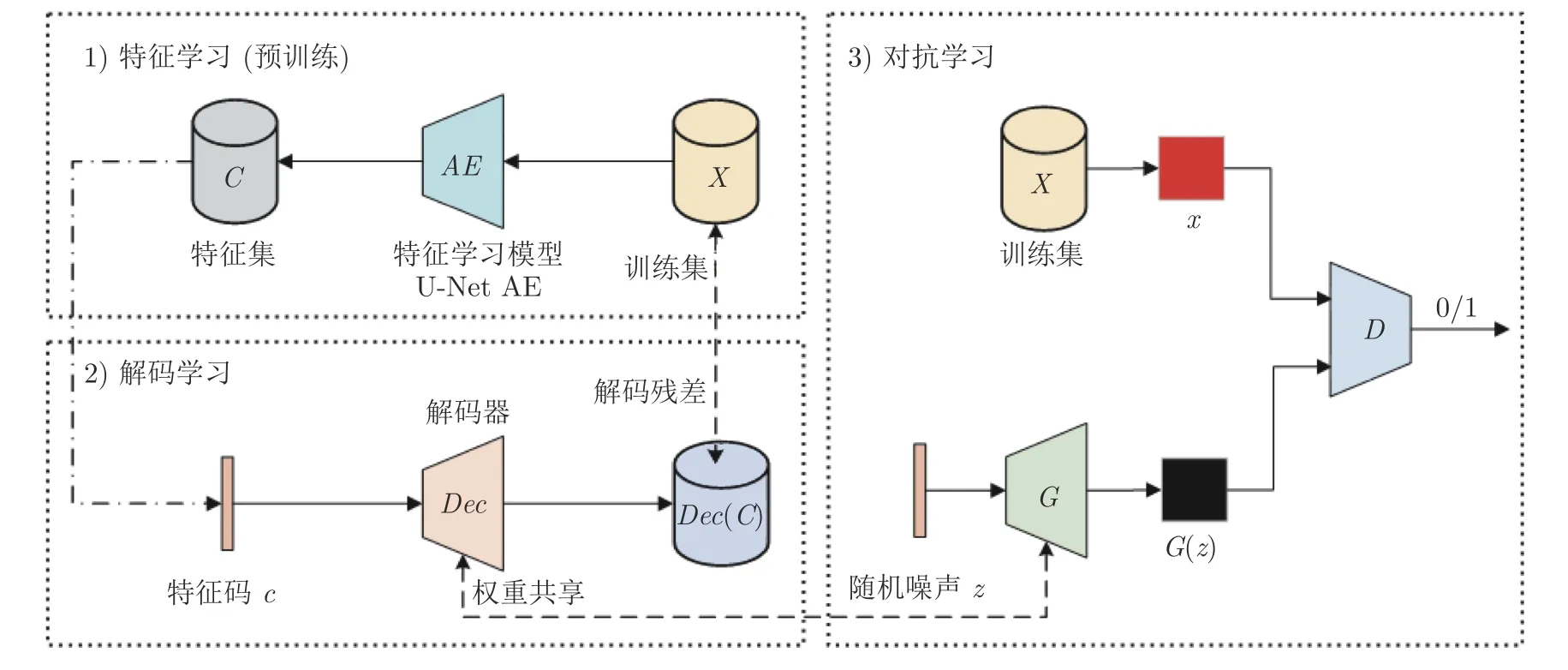
图1 总体结构示意图Fig.1 Overall structure sketch

2.2.1 特征学习

在图像特征学习中,需要提取出图像的隐含信息,用此表征原始图像.自编码特征学习是一种有效的图像特征学习方法[26].常用的自动编码机较多,除噪自动编码机[26-28]经过对训练样本加入噪声并进行降噪的训练过程,能够强迫网络学习到更加鲁棒的不变性特征,获得馈入图像的更有效和更鲁棒的表达.收缩自动编码机[26,29]能够较好地重构训练样本,并且对训练样本一定程度的扰动具有不变性.稀疏自动编码机[26,30]将稀疏编码和自编码机结合,可以提取馈入样本的稀疏显著性特征.对于一般任务,最常用的依然是经典自动编码机模型[26].

由于随机噪声z维度相对较低(如64 或100维),特征提取任务相对简单,且为获取更好的重构图像效果.本文将经典自动编码机结合U-Net 网络模型[31],建立了5 层的全连接类似U-Net 的自动编码机用于C的获取,并且使得特征c的维度与随机噪声z的维度是相同的.图2 给出了U-Net 型自动编码机用于获取X的特征集C的示意图.该网络由5 层神经元组成,第3 层用于特征提取,特征图像像素个数与随机噪声z维度相一致.

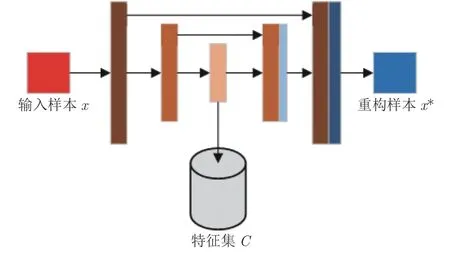
图2 特征学习网络结构图Fig.2 Structure diagram of feature learning network

训练过程中,损失函数选用均方差损失函数:

2.2.2 解码及对抗学习

设训练样本集X对应的特征集为C,解码器为Dec,它与G网络共享权重,网络结构一致.记X的概率密度函数为fX(x).解码集Dec(C)的概率密度函数为fDec(x).解码损失函数为:

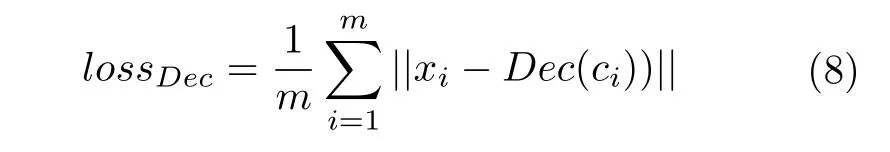
式中,xi为X中的样本,ci为xi对应于C中的样本,m为样本个数.||·||为度量两个样本的距离函数,常用的函数类型有L1 和L2 型函数.

在原有的JS 散度对抗损失函数中引入解码损失函数进行约束,需要控制解码约束条件对Dec网络梯度下降的贡献.主要原因有以下3 点: 1)G网络模拟的是训练集X的主要特征,不需要按像素严格一致.解码损失函数是按像素严格一致进行图像重构,因此后者约束更强势.2)对抗损失函数是优化JS(fX(x)||fG(x)),解码损失函数是优化KL(fX(x)||fDec(x)),优化后者虽然对避免JS(fX(x)||fG(x))为常数有益,但各自的梯度下降方向并不完全一致,应保证JS(fX(x)||fG(x))是主优化方向.3)优化二元组 (fX(x),fG(x))相 对于优化三元组(fX(x),fG(x),fDec(x)) 难度更低.当fDec(x)≈fG(x)时,相当于近似优化前者.

为达到以上目的,可以通过对解码损失函数权重系数,训练频次及学习率加以控制.当解码损失函数式(8)选用L2 型函数时,本文设计的解码损失函数如下:

式中,δ是判别函数,1 表示进行解码训练,0 表示屏蔽解码训练;λ是解码损失函数权重系数.

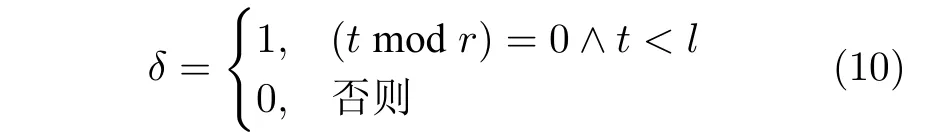
式中,t是当前的迭代epoch 数,r是控制调用解码约束的频次,l是控制最后一次解码的控制变量.每次对抗学习前,依据条件判别式(10)以此来控制解码约束条件的使用总次数和频率.

由此,最终的对抗网络损失函数为:

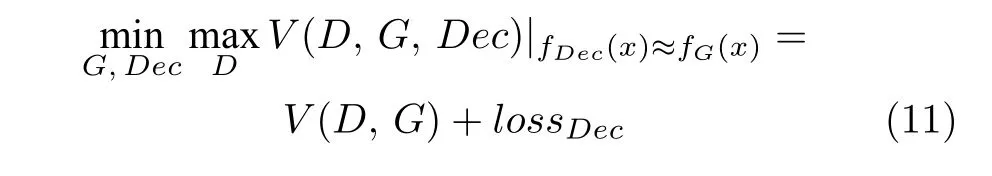
由于D网络是一个二分类网络,利用单向标签平滑[32]处理能对分类性能有一定提高,这有益于降低分类网络的训练难度.在实际训练操作中可以使用这种方式对式(1)进行标签平滑处理.

为使得上面所提供的解决方法有所依据.分析了以下3 点: 1)优化 J S+λ·KL 混合散度对JS 散度不为常数的影响.2)优化 J S+λ·KL 混合散度对优化原有JS 散度相对于分布对 (fX(x),fG(x))的极小值点及单调性的影响.3)优化KL 散度时解码损失函数类型选择的依据.为此下面3 个命题进行了讨论分析.

命题1.限制解码器Dec解码约束条件对Dec网络参数更新的梯度贡献,且使得fDec(x)≈fG(x).那么训练过程中引入解码约束条件有利于避免JS(fX(x)||fG(x)为常数.

证明.要证明命题结论,只需要证明引入约束条件后有利于fG(x) 相似于fX(x)即可.

记第t次解码训练后解码集Dec(C,t)对应的概率密度函数为fDec(x,t),第t次对抗训练后生成数据集G(Z,t) 对应的概率密度函数为fG(x,t).

由式(6)的C(G)条件知,G网络仅仅是使得fG(x) 模拟fX(x),并不要求G(Z)=X.所以优化过程是一个依分布收敛的过程,即:

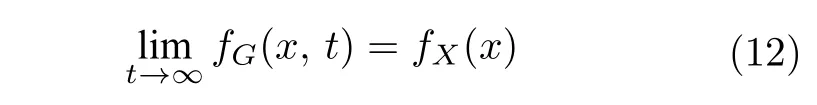
由式(8)可知,对于解码器Dec的理想目标是求解C→X的映射,使得Dec(C)=X,即:

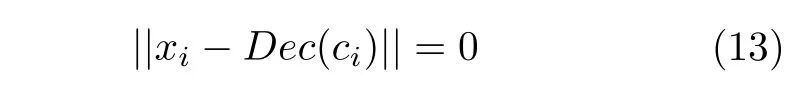
式中,xi和Dec(ci)分别是各自样本空间中的任意样本,且ci是xi的特征码.故而解码器Dec的理想目标是使得Dec(C,t)几乎处处收敛于X.但由于训练中,通常只能达到如下情况:

命题3.当训练集X符合正态分布时,解码器Dec应选用L2 型函数.

证明.记X对应的训练集为C,解码集为Dec(C).fX(x|c) 为C给定时,X的条件概率密度函数.fDec(x|c) 为C给定时,解码集Dec(C)等于训练集X的条件概率密度函数,那么解码器Dec解码的目的可表达为使得fDec(x|c)≈fX(x|c),即:

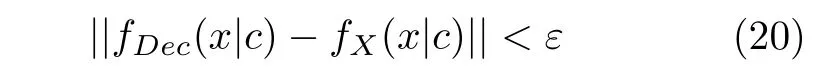
式中,ε是任意小的正实数.

其蕴含于(由KL 散度的信息论含义可得):

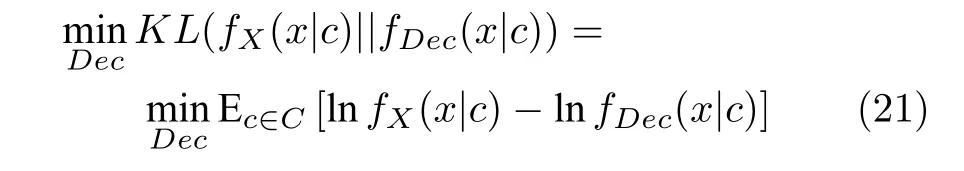
因为 lnfX(x|c) 为已知的训练集X及其对应的特征集C表达的信息.所以其为常数,在梯度下降优化时不对梯度做贡献.由此式(21)等价于优化下式:

由命题2 可知,引入解码约束条件基本不影响函数的单调性和极小值点,表明它们相对于分布对(fX(x),fG(x))的最优解一致,优化任务的总体目的相近.

由命题3 可知,若训练样本X符合正态分布,应选用均方差损失函数.由于训练集X中样本的结构信息(几何结构量)、颜色信息和清晰度(与图像纹理相关)等关键特征信息,依据三大中心极限定理可知是满足正态分布假设或近似正态分布假设.

2.3 网络训练

通过以上描述,可以得到整个网络的训练方法,如下所示:

步骤1.依据式(7)充分训练U-Net 型自动编码机,获取训练集X的特征集C.

步骤2.依据式(10)计算出判别值δ,如果δ=1 则对解码器Dec(解码器与生成器G权重共享,网络结构一致)使用均方根传播优化方法进行解码训练.每次馈入批量尺寸个x和对应的特征码c.

步骤3.分别馈入批量尺寸个x和G(z)到判别器D网络,使用均方根传播优化方法对其进行权重更新.

步骤4.馈入批量尺寸个z到生成器G网络,使用均方根传播优化方法对其进行权重更新.连续训练2 次G.

步骤5.重复步骤 2～4,直到达到最大epoch数为止.

3 实验及分析

本文实验中,选取的主要软硬件环境为,Tensor-Flow1.12.0 GPU 版本,CUDA 9.0,cuDNN 7.4,英伟达GTX1080,GTX1080Ti,RTX2080Ti 显卡.实验的其他部分如下.

3.1 评价指标及数据集

为定量对比分析多个生成模型的生成图像效果,选取Inception score (IS)[33-34]、弗雷歇距离(Frechet inception distance,FID)[33-34]和平均清晰度进行评价.IS 是评价生成图像的质量和模式类别多样性的指标(对多样性描述更准确一些),指标值越高越好.FID 也是评价生成图像质量和多样性,越低越好.计算IS 指标不需要训练集做对比,计算FID 指标需要训练集做对比,FID 越小表明与训练集的图像质量及多样性越接近.清晰度是图像重要的视觉质量指标,越高则有更多纹理结构信息.清晰度方法选取常用的基于能量梯度表达计算公式:

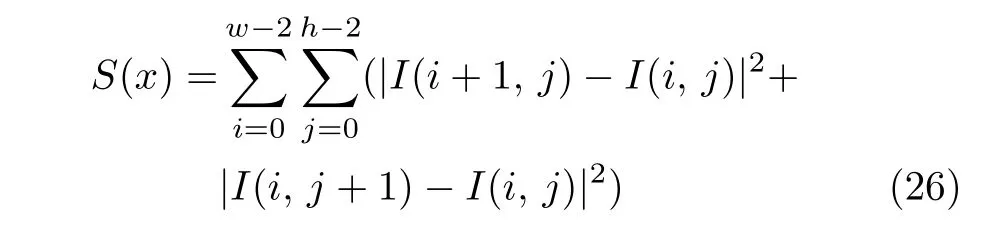
式中,I(i,j) 表示在图像样本x中坐标 (i,j)处的像素值大小,w和h分别表示样本图像x的宽度和高度.使用S(x)除以图像像素个数以获取平均清晰度.

为验证本文GANs 模型的生成图像的效果,选取Celeba 和Cifar10 数据集进行测试.数据集详细信息如下所示.

Celeba 数据集共含有202 599 张彩色人物上半身图像,每张图像大小为178×218 像素.在实验中选取前50 000 张图像,裁剪出64×64 的人脸图像作为训练集.Cifar10 数据集含有50 000 张训练集彩色图像和10 000 张测试集彩色图像.每张图片大小为32×32,10 个类别的图像在训练集和测试集中比例相同.实验选用Cifar10 的训练集作为GANs的训练集.图3～ 4 展示了训练集的样本图像.

图3 Celeba 数据集样本Fig.3 Samples of Celeba dataset

图4 Cifar10 数据集样本Fig.4 Samples of Cifar10 dataset

3.2 特征学习实验

在图像特征学习中,使用类似于U-Net 的5 层全连接自编码机用于特征学习,每层神经元数量为:w×h、1 0×10、1 0×10、1 0×10 和w×h(w和h是图像宽度和高度),激活函数为softsign,使用Adam 方法进行优化,学习率为0.001,动量因子为0.9.每批提取100 个样本图像的中间层特征,迭代次数为 7 000.在GTX1080Ti 显卡条件下,Cifar10数据集上所耗时间约为7 小时,Celeba 数据集上所耗时间约为18 小时.

图5 展示了部分训练样本重构效果和提取的特征图.前后3 行图像各为一个单元,每个单元中第1 行是原图,第2 行是重构图,第3 行是对应的特征图.在特征图中,每1 个格子对应原特征图的1 个彩色像素.

图5 U-Net 自动编码示例Fig.5 Samples of U-Net auto-encoder

由图5 可以看出,U-Net 结构下的自编码机都有比较好的图像重构视觉效果,所提取的隐含特征都有比较好的特征表达能力.从图5 可以观察出图像颜色和纹理结构越丰富,隐含特征色彩也越丰富.反之,特征的颜色也比较单一.例如图5 人脸图像中,第 1～4 列头发颜色和背景颜色都偏暗,面部方向为正面.第 5～8 列背景图像,面部角度及头发颜色都比较鲜明.与之对应,它们的特征也有比较明显的颜色区分度,从而表明所学习到的特征包含了原始图像的一些信息,如颜色和面部方向.在Cifar10 数据集中依然有类似的规律,能明显看出,后4 列图像是颜色鲜明的,特征也鲜明.

表1 给出了Celeba 和Cifar10 数据集重构样本与训练集的峰值信噪比(Peek signal to noise ratio,PSNR)和结构相似度(Structural similarity,SSIM)质量评估指标.

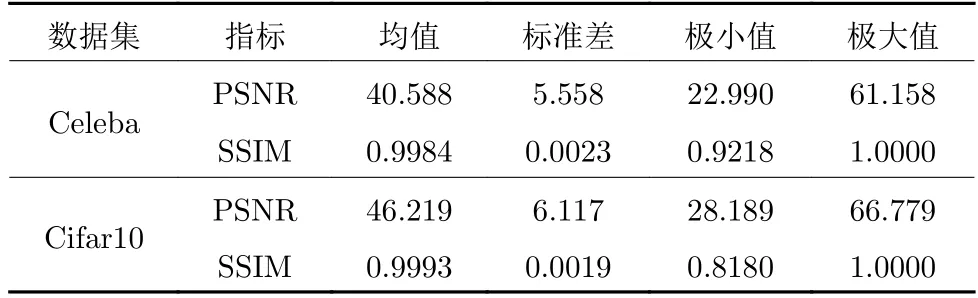
表1 原图像与重构图像的PSNR 和SSIM 值统计Table 1 PSNR &SSIM between original and reconstructed images

由表1 可以看出,在Celeba 和Cifar10 数据集上,U-Net 型自动编码机重构的样本在PSNR 和SSIM指标上都有不错的表现.结合图5 来看,其提取的特征具有训练集样本的特征表达能力.

3.3 不同解码实验对比

本节实验为验证样本特征有效性,限制解码约束条件的必要性及解码函数类型选择的重要性做了如下实验.1)正态特征(每个训练样本对应的特征符合标准正态分布);2)均匀特征(每个训练样本对应的特征符合[-1,1]的均匀分布);3) L1 解码约束条件.4) L2 解码约束条件,但不限制其对损失函数的梯度贡献.5)本文方法(L2 解码约束条件,限制对损失函数梯度贡献);除此,还计算了训练集的指标信息用以对比分析.

所有实验选用均方根传播优化方法,学习率为0.0002,动量因子为0.9,批量尺寸为64,epoch 数为15.在第1 至3 或5 组实验中,式(9)选取参数λ=1.0×10-7;式(10)中,r=2,l=11.在第4 组实验中,λ=1.0,r=1,l=epoch.Celeba 和Cifar10实验每组生成50 000 张图片进行统计分析.表2～3 展示了统计图像数据得到的各项指标结果,其中上标 * 项是来自不限L2 约束对损失函数梯度贡献权重实验,第5 列是计算与训练集清晰度均值的差距值,粗体表示最优值.

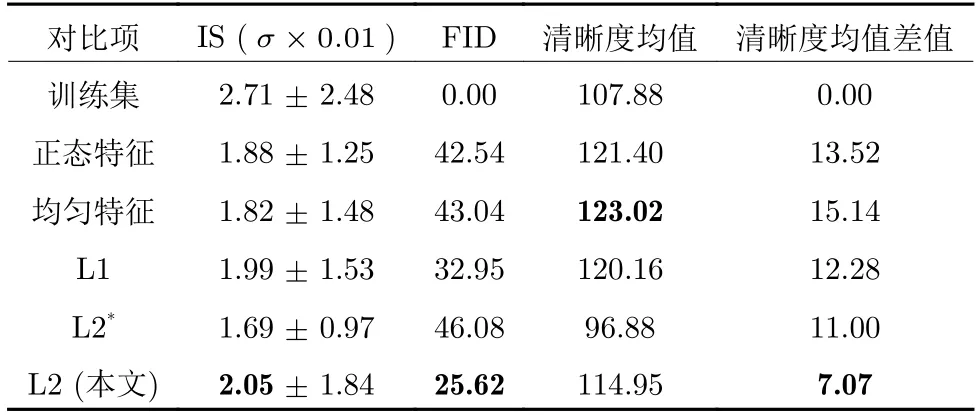
表2 Celeba 中不同解码实验结果Table 2 Results of different decoding experiments in Celeba

1)分析对于馈入图像特征c的必要性.对比表2～3 中的正态特征,由均匀特征和L2 (本文)表项可知,本文方法在IS 和FID 这两项关键指标上,均是最优.特别是在FID 指标上有显著提升,表明使用图像特征c进行解码是必要的,馈入的特征类型是不能随意选取.对比清晰度,本文方法的清晰度均值虽不是最大,但是本文清晰度更接近训练集的清晰度水平,表明能更合理地模拟训练集高频信息.

2)分析解码损失函数类型的必要性.对比表2～3 中L1 和L2 (本文)可知,IS 和FID 指标依然是本文占优.清晰度均值表项L1 约束占优表明其生成的图像填充的纹理信息更多,但本文方法清晰度依然最接近训练集清晰度.

3)分析限制解码约束条件对梯度贡献的必要性.对比表2～ 3 中L2*和L2 (本文)可知,L2*的IS 和FID 指标明显占劣势,这表明其多样性和生成图像的指标较差.对比清晰度指标可以发现不限制L2 约束条件对梯度的贡献,会影响生成图像的细节纹理填充.应注意表3 中L2*和训练集表项的清晰度均值相近的原因,前者是因为纹理细节丢失导致清晰度下降,后者是因为图像前景或背景本身纹理较少(如舰船、马匹、汽车、飞机等类别)导致整体清晰度下降.

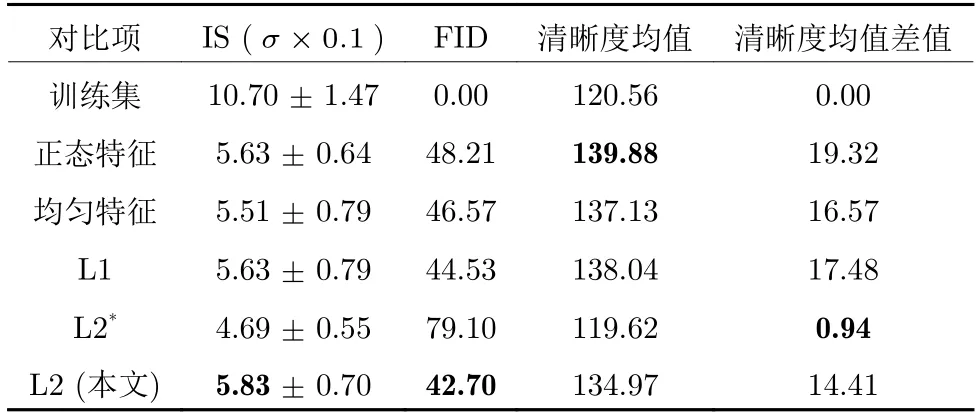
表3 Cifar10 中不同解码实验结果Table 3 Results of different decoding experiments in Cifar10

通过以上3 个方面的分析可以发现,本文方法中使用图像特征进行解码是必要的,馈入的解码特征类型不具有随意性;对于解码损失函数使用L2效果更优,具有一定必要性;限制解码损失函数对梯度的贡献,使得fDec(x)和fG(x)应近似相等是必要的.后两点也与模型的理论分析部分一致.

图6～ 11 展示了在Celeba 和Cifar10 数据集中,均匀特征、不限制权重的L2 约束以及本文方法实验生成样本.

图6 Celeba 中均匀特征实验样本Fig.6 Uniform feature experimental samples in Celeba

由图3 和图6～ 8 可以看出,本文方法(图8)生成的图像更细腻,图像纹理填充主要是填充到头发部分,视觉效果更好.而均匀特征生成的图像中(图6),一些纹理信息不仅填充到面部,而且还填充到背景区域,这也是表2 中其清晰度均值偏高的原因.表明它能够生成更多的纹理细节,但是填充位置未必合理.对于 L 2*生成的图像中(图7)能够发现,生成的样本比较模糊,纹理信息填充比较差,影响了视觉效果.表明限制解码损失函数对梯度下降的贡献是必要的.

图7 Celeba 中L2 解码不限制权重实验样本Fig.7 L2 decoding with not restrict weight experimental samples in Celeba

图8 Celeba 中本文方法实验样本Fig.8 Experimental samples of our method in Celeba

由图9～ 11 可以看出,本文方法(图11)能更明显地生成图像中背景和前景部分.而均匀特征生成图像(图9)纹理填充得更多.对于L2*生成的图像(图10)也能够发现图像相对模糊.通过以上的数据及生成图像对比分析表明,在本文方法中,为生成更好质量的图像,需要选取合适的解码特征类型,限制解码约束条件权重以及选取合适的解码函数类型.

图9 Cifar10 中均匀特征实验样本Fig.9 Uniform feature experimental samples in Cifar10

图10 Cifar10 中L2 解码不限制权重实验样本Fig.10 L2 decoding with not restrict weight experimental samples in Cifar10

图11 Cifar10 中本文方法实验样本Fig.11 Experimental samples of our method in Cifar10

3.4 耗时分析

本文GANs 所使用的G和D网络内部结构均与DCGANs 一致,并且本文将JS 散度作为主优化目标,后者将JS 散度作为优化目标.为验证模型的所耗时间代价,在同一台含GTX1080Ti 显卡的计算机上测试了DCGANs 和本文GANs 模型的耗时,以此对比分析出本文的训练时间代价.

由表4 可以看出,在预训练出训练集样本特征前提下,本文GANs 总耗时有所下降,这得益于总的epoch 数减少.但单位耗时有所提高,这源于本文GANs 在某些epoch 训练周期内会使用解码约束条件.由第3.3 节实验设置可以看出,解码约束的使用仅在0 和0 到11 之内的偶数训练周期中,共6 次.在特征提取的过程中,由第3.2 节可知,其耗时远大于用于解码和对抗训练耗时.表明本文GANs 在特征学习过程中的预训练耗时代价较大.总耗时的减少为模型的参数调试带来了比较大的便利.

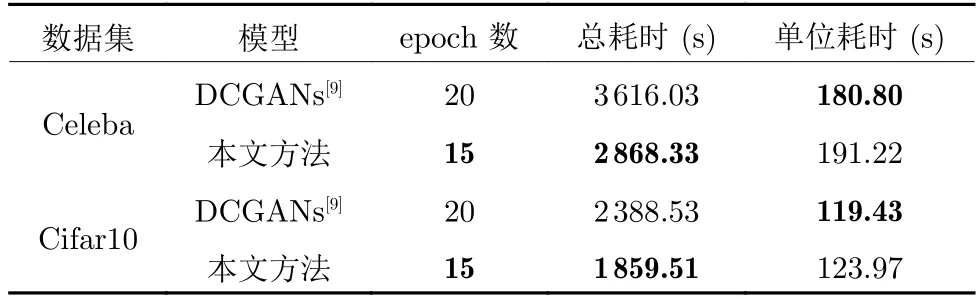
表4 时间代价测试Table 4 Test of time cost

3.5 不同GANs 实验对比

在对抗训练实验中,本文选取的G网络和D网络结构与DCGANs 一致,LSGANs、WGANs 和WGANsGP 的网络结构处理方法相同.选取均方根传播优化方法,学习率和动量因子分别为0.0002和0.9.

BEGANs 和SAGANs 分别依据文献[16,23]代码单独实验,关键参数与原文一致,选用Adam优化.所有实验中批量尺寸为64.在Celeba 和Cifar10 上每组实验均生成50 000 张图片进行数据统计,获得表5～ 6 实验数据.在表5～ 6 中,SAGANs1使用WGANsGP 损失函数(优化沃瑟斯坦距离),SAGANs2使用DCGANs 损失函数(优化JS 散度);关于本文所设计GANs 参数统计,前半部分是解码及对抗学习模型参数量,后半部分是U-Net 自动编码机模型参数量.

对比分析表5 实验数据可知:

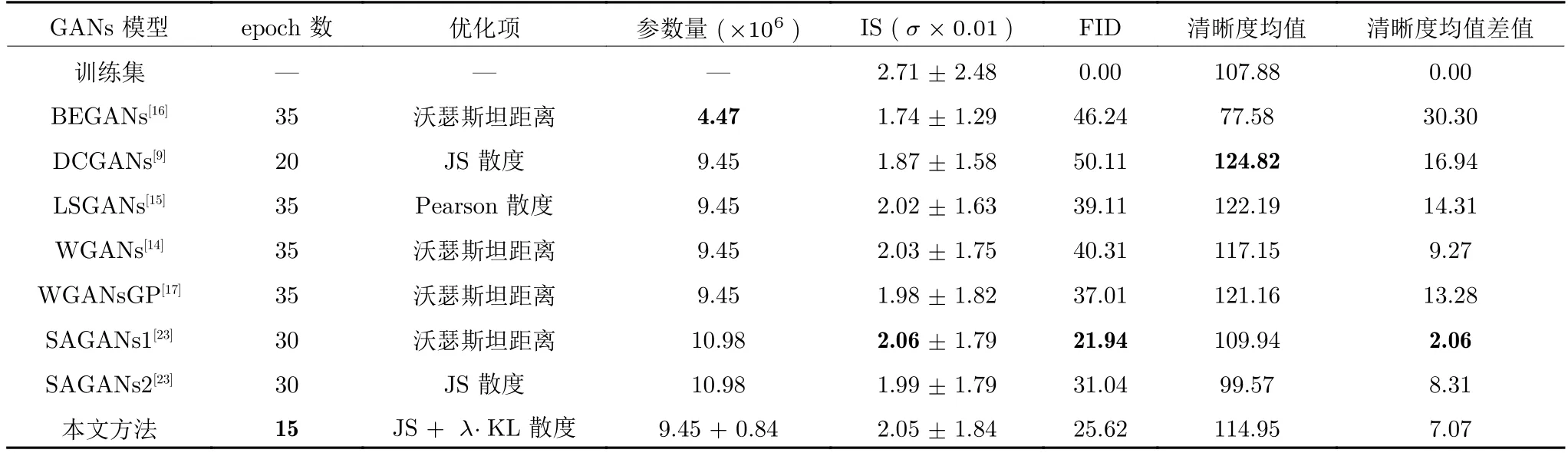
表5 Celeba 中不同GANs 对比Table 5 Comparsion of different GANs in Celeba

1)对比前5 个和本文GANs 模型.由IS 指标可以看出,本文虽稍好于LSGANs、WGANs 和W G A N s G P,但它们之间I S 指标基本一致;DCGANs 和BEGANs 较差,表明两者多样性和质量差于其他方法.在FID 指标上,本文GANs模型明显优于这5 个GANs 模型,表明本文GANs模型相对地更能有效模拟训练集分布.在清晰度指标上,虽然清晰度均值不是最大,但是它与训练集之间的清晰度均值差距更小,表明本文GANs 对高频细节模拟更合理.对比模型参数可知,由于特征学习网络的参数量较少,所以本文GANs 模型并没有明显增加参数量.最后对比epoch 数可以看出,本文相对于上述GANs 模型有明显优势.

2)对比SAGANs 和本文GANs 效果.从SAGANs1 和本文GANs 的实验数据可知,优化沃瑟斯坦距离的SAGANs 的综合性能很好,IS 指标与本文相当,FID 指标稍好于本文GANs;在清晰度指标上,它能更合理地模拟人脸纹理信息,虽然参数量两者基本一致,但其训练epoch 数明显多于本文GANs模型.再对比SAGANs2 和本文GANs 可知,本文综合效果又较明显优于优化JS 散度的SAGANs模型.说明当JS 散度作为优化目标或主优化目标时,本文GANs 模型比融入注意力机制和谱归一化优化的SAGANs 模型表现更佳.同时,通过对应地对比DCGANs 与WGANs、SAGANs1 与SAGANs2,可以看出,优化JS 散度模型生成图像质量差于优化沃瑟斯坦距离模型生成图像质量.这也证明了WGANs[14]的分析,JS 散度的确可能带来梯度消失问题,导致生成图像质量下降.

由表6 可知,在Cifar10 数据集中依然存在上述类似的实验现象,但从统计的数据来看,没有单类别数据集那么明显.

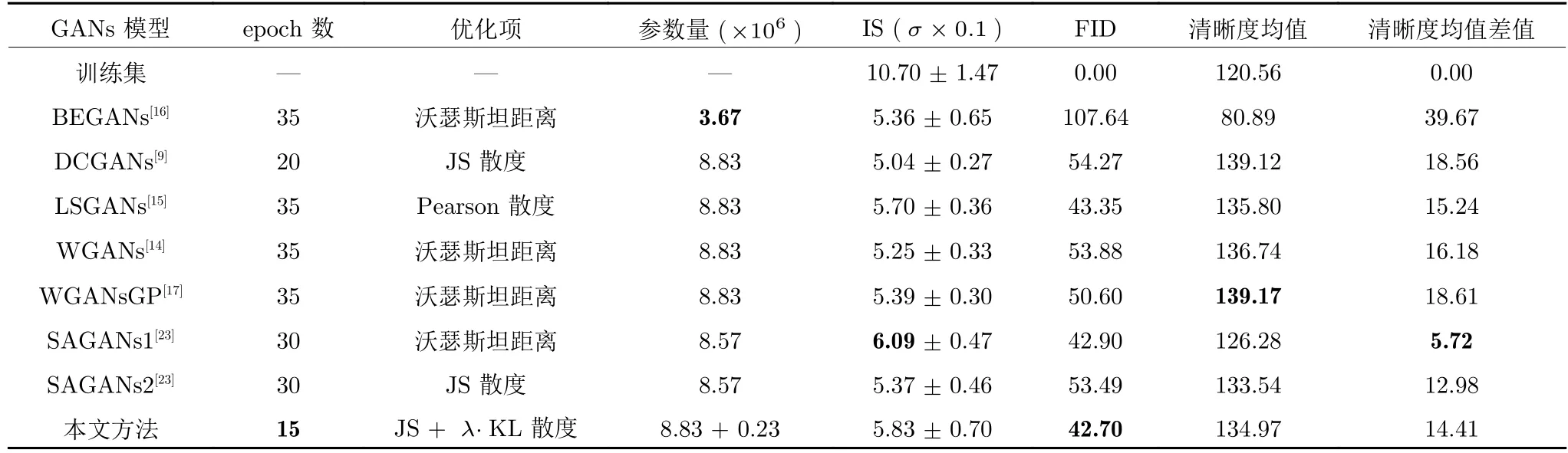
表6 Cifar10 中不同GANs 对比Table 6 Comparsion of different GANs in Cifar10

通过以上实验数据及分析可知,本文GANs 综合性能达到除了优化沃瑟斯坦距离的SAGANs 外的最优效果.相对而言,本文GANs 在仍以JS 散度为主优化目标时,模型综合性能靠近优化沃瑟斯坦距离的SAGANs,并且网络结构并没有使用注意力机制和谱归一化优化.同时在预训练提取出训练特征的前提下,本文GANs 模型明显减少epoch 数.

由图12～ 19 的展示,可以直观地对比BEGANs、DCGANs、WGANsGP 和SAGANs1 的GANs 生成效果.

图12 Celeba 中BEGANs 实验样本Fig.12 Experimental samples of BEGANs in Celeba

图13 Celeba 中DCGANs 实验样本Fig.13 Experimental samples of DCGANs in Celeba

图14 Celeba 中WGANsGP 实验样本Fig.14 Experimental samples of WGANsGP in Celeba

图15 Celeba 中SAGANs1 实验样本Fig.15 Experimental samples of SAGANs1 in Celeba

图16 Cifar10 中BEGANs 实验样本Fig.16 Experimental samples of BEGANs in Cifar10

图17 Cifar10 中DCGANs 实验样本Fig.17 Experimental samples of DCGANs in Cifar10

图18 Cifar10 中WGANsGP 实验样本Fig.18 Experimental samples of WGANsGP in Cifar10

图19 Cifar10 中SAGANs1 实验样本Fig.19 Experimental samples of SAGANs1 in Cifar10

对比分析使用Celeba 数据集训练GANs 而生成的图像.由图12 可知,BEGANs 虽然能很好对形态特征进行学习,但的确存在比较严重的高频信息丢失现象,并且生成的图像出现斑块.由图13～ 14可知,DCGANs 和WGANsGP 生成的图像纹理信息填充区域过多,比如训练图像面部的高频信息较少,但是生成图像存在面部填充高频信息的现象,这也是表4 对应的清晰度均值项偏高的原因之一.图15 能很明显地观察到优化沃瑟斯坦距离的SAGANs 生成的图像,在面部形态和纹理等特征更合理,并且结合图8 (本文效果),也能发现更好地生成图像样本,其形态和纹理等信息都比较协调.对比Cifar10 数据集生成的图像,除图16 可以明显看出差异外,难以直接进行视觉评估,在第3.5 节和表6 数据进行了分析.

综上所述,本文方法(JS +λ·KL 散度) 相对于DCGANs (JS 散度)有较明显的提升,在IS 指标上也能达到LSGANs (Pearson 散度)、WGANs(沃瑟斯坦距离)等GANs 模型的图像生成效果,并且在FID 指标上进一步有所提高.此外,本文方法生成的图像效果能逼近优化沃瑟斯坦距离的SAGANs图像效果,并且参数量并没明显增加.在训练集样本特征预学习完成后,解码及对抗学习能有效减少训练所需的epoch 数.

4 结束语

为提高GANs 图像生成质量,考虑到JS 散度可能为近似常数时带来对生成图像效果的不利影响,本文尝试通过增加样本特征解码约束条件来减弱这些影响.实验结果表明,利用样本特征解码约束条件进行对抗训练的约束,有利于图像生成质量提高和减少epoch 数.同时,本文方法能够更合理地模拟训练集的高频信息部分.本文方法需对训练样本预学习出样本特征,虽较少地增加了网络参数量,但需要较多的特征提取预训练时间.对于其他特征提取方法,特征分布与随机噪声分布的关系对生成效果的影响值得进一步研究.