基于核心素养的高中数学教材习题对比研究——以“三角函数”为例

朱晓琳

（青海师范大学 青海西宁 810016）

引言

近年来，学科核心素养成为高中教育领域、教育研究领域的热点话题。由于自身的性质和特点，数学学科核心素养被概括为六个方面：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析。在价值方面，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现[1]。需要注意的是，在课程标准的附录1中，数学核心素养的六个方面又被划分为了程度依次递进的水平一、水平二、水平三三个水平，各个素养的不同水平也有相对应的文字说明。这是我们下面进行习题研究的依据。

随着课程标准的再次修订以及新版教材的问世，此方面的研究也需要在原有的基础上加以更新。本文根据课程标准中阐述的数学学科核心素养内涵及三种水平，对新人教A版和北师大版高中数学教材中的“三角函数”一章习题进行对比研究，主要探讨两个问题：一是两版教材习题在体现的数学核心素养类型上的差异；二是两版教材习题在体现的数学核心素养水平上的差异。

一、研究设计

1.研究对象

根据现行教材的使用分布情况，本研究选取2019年教育部审定通过的人民教育出版社（简称“新人教A版”）出版的高中数学教材和北京师范大学出版社（简称“北师大版”）出版的高中数学教材“三角函数”一章（本章位于“新人教A版”高中数学教材必修第一册第五章，“北师大版”高中数学教材必修第二册第一章）全部习题，包括：“练习”“习题”和“复习题”（或“复习参考题”）的全部题目。“新人教A版”高中数学教材“三角函数”一章习题总数为199，“北师大版”高中数学教材“三角函数”一章习题总数为155。

2.研究设计

（1）研究假设

本研究假设研究对象中的每道题目至少蕴含一种数学核心素养。从图形或者实际情境中抽象出三角函数模型解决相关问题涉及数学抽象素养；借助三角函数图象判断任意角三角函数值的正负性等问题涉及直观想象素养；弧度制与角度制之间的转换，利用诱导公式和三角恒等变换求解式子和证明等式涉及逻辑推理和数学运算素养；利用函数模型解决现实情景问题体现了数学建模素养。数学核心素养中，“数据分析”素养与“三角函数”部分没有明显联系，故不考虑该核心素养。综上分析可见，本研究的假设是成立的。

（2）对习题核心素养类型的划分

对习题核心素养类型的划分标准是课程标准中阐述的各素养的内涵。在界定本章习题素养类型的时候，我们发现，部分题目蕴含两种及以上核心素养。究其原因，数学核心素养之间是相互联系的。对于这种情况，本文进行说明：在确定习题数学核心素养类型时，根据题目的性质优先选择重点考查的核心素养，对于综合考查多种数学核心素养的题目，可以同时选取多个核心素养。

数学核心素养类型划分示例：

此题需要借助函数图象判断两函数的交点个数，其中，t不是确定值，是需要进行讨论的。所以，本题体现了直观想象与逻辑推理两种核心素养。

（3）对习题核心素养水平的划分

在确定了题目的核心素养类型之后，接下来就是需要确定题目体现的核心素养类型所处的水平。这里，本文需要再次作出说明：某习题的核心素养总体水平确定为本题所涉及的多个核心素养类型中水平的最高值。

本题只需要正确运用正切的诱导公式展开：

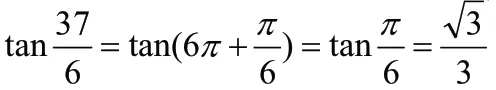
考查对正切诱导公式的简单应用，所以将此题归结为数学运算的水平一范畴。

本题需要根据学生从顶角余弦出发，选择合适的诱导公式、三角恒等变换以及倍角公式设计运算过程解答，所以将此题归结归结为数学运算的水平二范畴。

3.编码与数据统计方法

（1）编码方法

分别用RA、BS代表新人教A版和北师大版高中数学教材，用数字1、2、3分别表示水平一、水平二、水平三。用RA1，RA2，…，RAn表示新人教A版教材的第1，2，…，n题；用BS1，BS2，…，BSn表示北师大版教材的第1，2，…，n题。

（2）数据统计方法

在核心素养类型上，统计出每版教材中体现各个素养的习题总数，然后除以该教材“三角函数”一章习题的总数，得到该教材习题在各个核心素养类型上的比重。

在核心素养水平上，从两方面进行统计。一方面，统计出每版教材中各个核心素养类型下不同水平的题目个数，然后除以对应核心素养类型的习题总数；另一方面，分别统计出两版教材中处于水平一、水平二、水平三的题目的数量，除以对应教材“三角函数”一章习题总数，得到两版教材“三角函数”一章习题在水平一、水平二、水平三上的数量比重。

二、数据结果

1.在核心素养类型上的统计结果

两版教材“三角函数”一章习题在五个核心素养类型上的统计结果见表1及图1。

表1 两版教材“三角函数”习题在核心素养类型上的题目数量及比重

图1 两版教材“三角函数”习题在核心素养类型上的数量比重（%）

2.在核心素养水平上的统计结果

两版教材“三角函数”习题在五个核心素养水平上的统计结果见表2和表3。

表2 两版教材“三角函数”习题在各核心素养不同水平上的题目数量（个）

表3 两版教材“三角函数”习题在各核心素养不同水平上的题目比重（%）

两版高中数学教材“三角函数”习题在三水平的比重见表4。

表4 两版教材“三角函数”习题在三水平上的题目数量及比重

三、研究结论

1.在核心素养类型上的结论

（1）两版教材“三角函数”习题在逻辑推理和数学运算素养上的比重较高

根据表1和图1，可以看出，两版教材“三角函数”习题在逻辑推理素养和数学运算素养方面的比重相对较高。其中，在数学运算素养上的比重最高，新人教A版教材“三角函数”习题在数学运算素养上的比重为71%，是两版教材“三角函数”习题在各核心素养类型上的最高比重。北师大版教材“三角函数”习题在数学运算素养上的比重为63%。

两版教材“三角函数”习题在数学抽象和数学建模素养方面的比重相对较低。北师大版教材“三角函数”习题在数学建模素养上的比重是最低的2%。

（2）两版教材“三角函数”习题在核心素养类型上存在差异

进一步研究发现，在数学运算素养方面，新人教A版教材的题目比重（71%）高于北师大版教材的题目比重（63%）。可见，新人教A版教材更加强调学生通过准确运算理解巩固知识和解决问题的能力；在直观想象素养方面，北师大版教材的题目比重（20%）明显高于新人教A版教材的题目比重（8%）。

2.在核心素养水平上的结论

（1）两版教材习题素养水平大都处于水平一、水平二，少数习题处于水平三

由表4可知，两版教材“三角函数”习题在核心素养水平上大都处于水平一和水平二，少数习题处于水平三，且在水平一上的比重均高于在水平二上的比重。在水平一、二上，北师大版教材“三角函数”习题的比重（97%）相对较高。在水平三上，新人教A版教材习题的比重（10%）相对较高。

（2）两版教材习题在各核心素养的各水平上各有侧重

在数学抽象素养方面，两版教材“三角函数”习题在三水平上分布相对均衡。在水平一上，北师大版教材“三角函数”习题的比重（38%）相对较高。在水平二、三上，新人教A版教材“三角函数”习题的比重（31%和44%）相对较高。

在逻辑推理素养方面，两版教材“三角函数”习题主要分布在水平一、二，且在水平二上的比重（54%和66%）最高。北师大版教材“三角函数”习题未涉及水平三。在水平一上，新人教A版教材“三角函数”习题（40%）的比重相对较高。在水平二上，北师大版教材“三角函数”习题的比重（66%）相对较高。

在数学建模素养方面，新人教A版教材“三角函数”习题在三水平上均有分布，且在水平三上的比重（50%）最高。北师大版教材“三角函数”习题均分布在水平二。

在直观想象素养方面，新人教A版教材“三角函数”习题主要分布在水平一，北师大版教材“三角函数”习题主要分布在水平二。两版教材“三角函数”习题均未涉及水平三。

在数学运算素养方面，两版教材“三角函数”习题主要分布在水平一、二，且在水平一上的比重最大。在水平一上，北师大版教材“三角函数”习题的比重（73%）相对较高。在水平二上，新人教A版教材“三角函数”习题的比重（39%）相对较高。

四、结语

1.对新人教A版教材“三角函数”习题的编写建议

（1）适当提高体现直观想象素养的习题比重

基于直观想象素养方面，北师大版教材“三角函数”习题的题目比重显著高于新人教A版教材“三角函数”习题的题目比重这种情况。对直观想象的考查习题，主要分布在对三角函数的图象的考查中，三角函数图象相关内容隶属于三角函数的性质，属于核心的考点[2]。对于新人教A版教材“三角函数”习题而言，建议适当提高体现直观想象的习题比重。

（2）适当提高居于水平二的习题比重

基于新人教A版教材“三角函数”习题在水平一上的比重高于在水平二上的比重这种情况，同时考虑到数学核心素养水平二是高考命题的依据。建议新人教A版教材在保证居于水平一的“三角函数”题目比重的前提下适当提高本章居于水平二的体现数学运算、数学建模、数学抽象和直观想象素养习题的比重，以此发展学生的相关核心素养。

2.对北师大版教材“三角函数”习题的编写建议

（1）适当提高体现数学建模素养的习题比重

基于在直观想象素养方面，新人教A版教材“三角函数”习题的题目比重高于北师大版教材“三角函数”习题的题目比重这种情况。对于北师大版教材“三角函数”习题而言，建议适当提高体现数学建模的习题比重，提高学生数学学习的热情。

（2）适当提高居于水平二的习题比重

基于北师大版教材“三角函数”习题在水平一上的比重高于在水平二上的比重这种情况，同时考虑到数学核心素养水平二是高考命题的依据[3]。建议北师大版教材在保证居于水平一的“三角函数”题目比重的前提下适当提高本章居于水平二的体现数学抽象和数学运算素养的习题比重，提高学生的抽象概括和运算能力，帮助学生更好地理解和掌握知识。