基于统计分析阈值的航段油耗分段线性估计模型

刘志， 陈静杰

(中国民航大学电子信息与自动化学院， 天津 300300)

航空器碳排放量核查的实质是对飞机油耗的估计。航程是影响飞机油耗的重要因素，两者间呈现复杂的非线性特征，不仅表现在全航程下的航班油耗呈显著非线性，而且对于单一航段下的航班油耗同样也呈现出非线性特征，其原因是由于诸如业载的不同以及运行的大气环境等其他因素的影响。该非线性复杂特征为合理、准确判断航空运输过程碳排放量进而有效控碳带来了诸多困难。如何发展一种既考虑上述因素而又不必在判断方法或判断模型中显性形式参数出现，从而使模型简化，进而利于碳排放量核查，这样的解决方案值得探索。

从航司与航班层面分别阐述对于碳排放与油耗估计的研究现状。从航司方面，Wang等[1]基于全球松弛度的度量模型和全球Malmquist-Luenberger生产率指数调查了碳排放的静态和动态效率；Cui等[2]根据全球航司的实际数据，运用BP(back propagation)神经网络对数据进行预测，构建一个DEA(data envelopment analysis)模型来计算减排分配比例。上述方法是从航司层面探讨碳减排问题，未涉及对航班排放的考察，无法从运输过程全要素中探讨运行碳排放减缓的行为，缺少对航班碳排放集合的微观刻画。

从航班层面，Zhang等[3]通过拟合QAR(quick access recorder)数据的实际飞行数据提取启动参数之间的关系，针对起飞爬升阶段提出一种燃油消耗模型；熊欢等[4]公开了一种小样本训练数据条件下的飞机巡航燃油耗量测量方法；刘家学等[5]提出一种基于DBN(deep belief network)模型的飞机下降阶段油耗估计方法；陈静杰等[6]提出一种重构样本下飞机油耗增强自适应差分进化相关向量机的预测方法，并构建飞机油耗预测模型；Huang等[7]通过对机载飞行数据记录器和自动相关监视广播的飞行数据建模，探索了一种估算飞机燃油消耗的新策略；胡杨[8]建立一种基于分位数回归的航线油量预测模型；文献[9]提出了一种独特的方法量化其节油性，并提供了在试飞前无需建模就可以评估燃油的新方法；姚若霖等[10]分析各飞行阶段飞行小时与油耗特征，建立飞机油耗区间估计，并根据航线飞行小时的季节性特征，提出一种基于飞行小时的航线油耗预测方法。上述方法多针对航段内航班各阶段油耗的非线性展开讨论，几乎未涉及讨论油耗影响因素对油耗量具体表现的非线性复杂特征。

为此，现构建一种基于统计分析阈值的运输过程航段油耗分段线性估计模型。在飞机运输过程航段油耗高阶多项式表达的基础上，以全航程航段油耗核证重要性指标为统计分析阈值来设定多项式表达线性化分段的依据，构建起航段油耗分段线性估计模型，使得该模型兼顾科学计算准确性与核证实操合理性。

1 航程油耗的非线性统计与合理性分析

1.1 航段油耗非线性统计分析

1.1.1 全航程航段油耗非线性统计分析

图1为某机型各航程(以航段距离表示，即下文的航段)航班油耗量分布图。航段较短的情况下，航班油耗量增加得相对缓慢；航段较长的情况下，航班油耗量增加得则极为剧烈。由此可得出，全航程航段的航班油耗量呈现为先缓慢增加后逐渐递增的趋势，即全航程航段油耗呈现显著非线性特征。

图1中的每一个点代表一架航班的航班油耗量，且每架航班的油耗量均不相同，体现出不同航段航班油耗量的不连续性。根据图像所呈现出的整体特征，采用分段线性来描述不连续区域的方式是可行的，做该处理后，分段点前后的油耗估计则可转变为在一定区间内的连续油耗估计，该区间的限制条件为

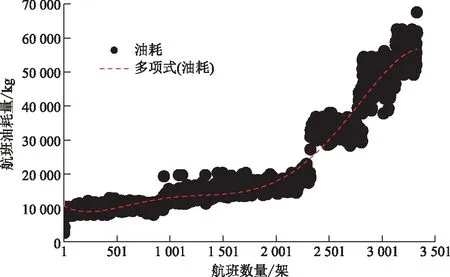
图1 某机型各航班油耗量分布Fig.1 Fuel consumption distribution of each flight of a certain aircraft type

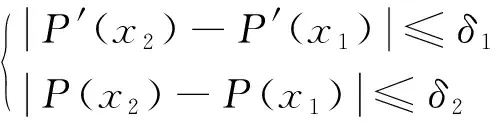
(1)

式(1)中：P′(x)表示多项式函数的导数值；P(x)表示的是多项式的函数值;δ表示满足不等式成立的微小量。式(1)表示的是分段点前后某个区间内导数和区间端点油耗量差值的限制性条件，其中，选择δ1的取值范围为[0.001，0.005]，δ2的取值范围为[100，150]。另外，该限制条件的取值范围可根据实际情况进行调整。

1.1.2 单一航段油耗非线性统计分析

为说明单一航段油耗的特征，现给出某一航段油耗的航班油耗量示意图，如图2所示。可知，每架航班对应的航班油耗量不同，产生这一现象的可能原因有飞机的飞行姿态、侧风的影响、大气温度以及绕飞的情况等。由此可见，单一航段油耗也具有非线性特征。

航班油耗量不仅在总体上呈现出显著的非线性特征，同时，对于单一航段而言，航班油耗量也呈现出非线性特征。综上所述，航程油耗具有复杂的非线性特征。

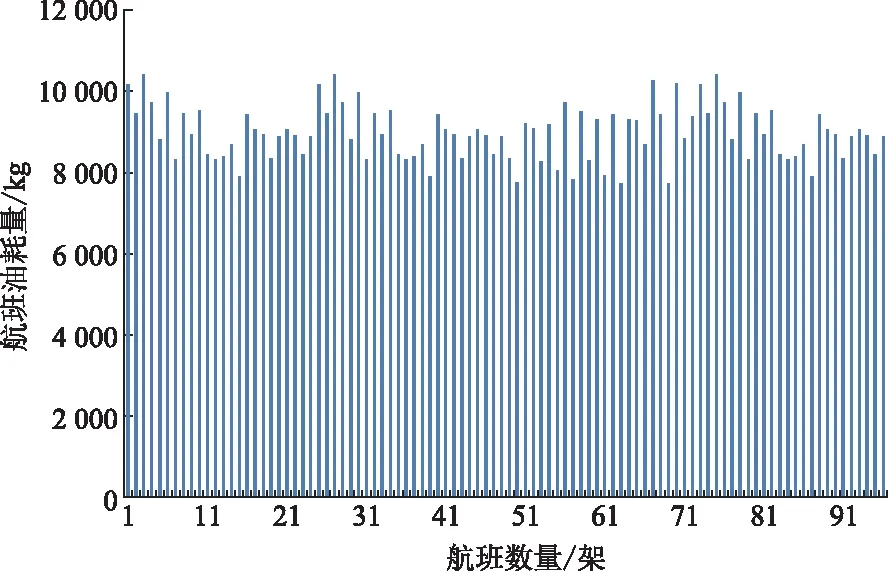
图2 北京—长春航班油耗量Fig.2 Fuel consumption of Beijing—Changchun flight

1.2 航段油耗的碳核查合理性分析

图3为航班油耗与航程的散点图。当航程不同时，对航班油耗量的影响也不同。图中能够看出以下两种特征：一方面，飞机在飞不同的航程时，所消耗的燃油量明显不同，燃油消耗量的大小随航程的增加而增加；另一方面，飞机在飞相同的航程时，所消耗的燃油量同样也呈现出显著的差异，这一情况尤其体现在飞机飞长航程时。

当航程超过4 000 km时，所表现出来的最大燃油消耗量与最小燃油消耗量的差值为10～20 t，其数据分散程度的统计指标数据如表1所示。

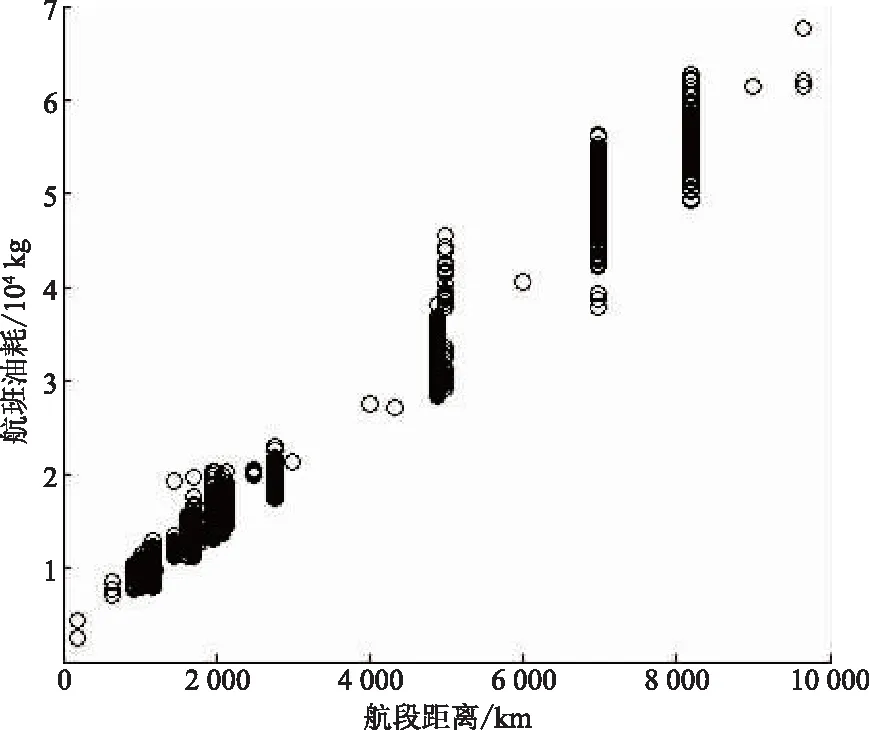
图3 航班油耗和航程分布Fig.3 Distribution of flight fuel consumption and range

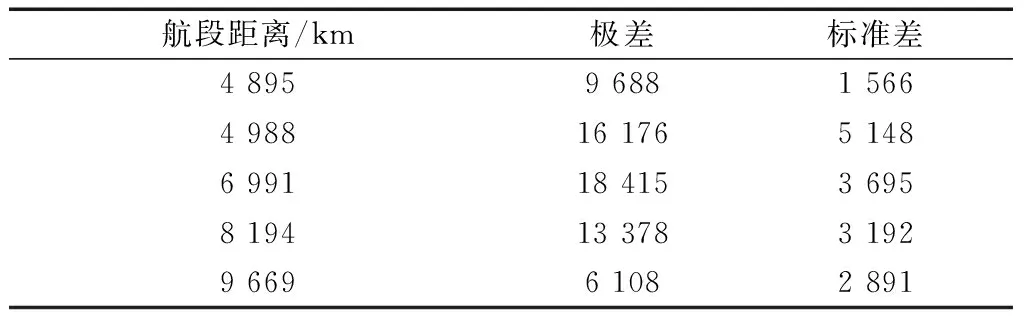
表1 全航程油耗数据分散程度统计量指标Table 1 Statistical index of dispersion degree of fuel consumption data in the whole voyage

在1.1节中已说明航程油耗间具有复杂的非线性特征，而图3表示的是航班油耗与航程的具体分布，航程油耗数据不连续，且某些航段不存在油耗数据，也从另一个角度反映了航程油耗数据的复杂非线性。图3中在某些航段内没有航班油耗数据，是因为在这些航段内航路没有开通，若在这些区域内做油耗估计，那么将会削弱油耗估计的合理性。因此，可将这些区域作为航程油耗估计的限制条件。

2 非线性的线性化

2.1 航段油耗分布性态分析

判断数据序列的分布性态可用偏度与峰度来评价。其中，偏度是用来帮助判断数据序列的分布规律性的指标，而峰度则是一个用于衡量分布平坦性的度量指标。

现以从北京到广州这一条航段为例，说明该航段的分布性态，其各项指标结果如表2所示，分布性态曲线如图4所示。

从表2中看到从北京到广州这一航段上航班油耗量的均值、中位数与众数均不相同，说明数据序列的分布不对称；从峰度与偏度的值可以看出，峰度大于0，偏度也大于0，其分布曲线性态属于右偏尖顶峰，这一性态体现在图4中。由此得出北京—广州这一航段上的油耗分布为偏态分布。而在偏态情况下，选择中位数来代表从北京到广州这一航段的航班油耗量。其余航段的航班油耗量均可按照上述方式做筛选。

此时，经过分布性态分析后各航段航班油耗如图5所示。根据相邻航段的航班油耗波动程度，削弱全航程航段油耗的非线性，用分段线性来代替非线性是可行的。

表2 北京—广州航段油耗各指标结果Table 2 Fuel consumption index results of Beijing-Guangzhou Segment

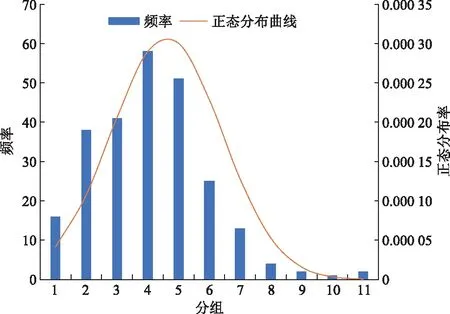
图4 北京—广州航段油耗分布性态图示Fig.4 Fuel consumption distribution behavior diagram of Beijing—Guangzhou segment

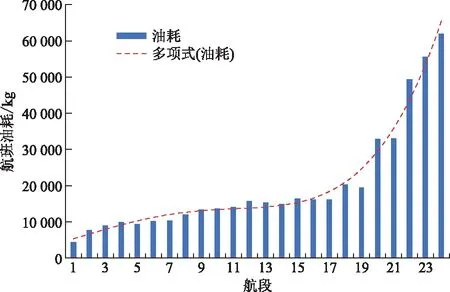
图5 各航段航班油耗量Fig.5 Fuel consumption of each flight segment

2.2 油耗的非线性估计

在1.1节中已说明航程与油耗间存在非线性关 系，而在所有数据拟合的方法当中，最小二乘法拟合是已被证明的应用最为普遍的方法。因此，采用多项式拟合的方法对航程油耗进行非线性估计。其非线性表达式为

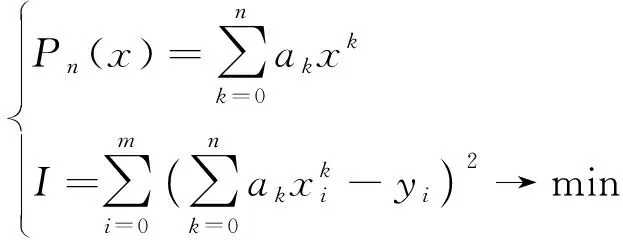
(2)

式(2)中：ak为多项式的系数；(xi,yi)为航程与航班油耗组成的点；第二个式子表示使得(xi,yi)到Pn(x)(即多项式拟合函数)的距离和达到最小。

由式(2)可知，该式子为a0,a1,…,an的多元函数，因此高阶多项式拟合就可以转化为求解I=I(a0,a1,…,an)的极值问题。

依据多元函数求解极值的原理，关于a0,a1,…,an的线性方程组，可以用矩阵描述为

(3)

观察方程组(3)的系数矩阵，很明显，系数矩阵属于对称正定矩阵，因此，可以得到唯一的系数矩阵，即多项式表达是唯一的。经过多项式拟合后，可得到对应的非线性估计模型，即油耗的非线性估计。

2.3 非线性的分段线性化

为降低非线性估计模型的复杂性，将非线性进行分段线性化。求其多项式函数的导数公式为

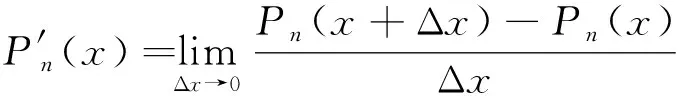
(4)

寻找其统计分析阈值为

(5)

多项式导数差的绝对值表示的是多项式函数的变化率，当该变化率达到限制条件时，说明多项式函数在某一区间内存在分段点；于此同时，当多项式函数差的绝对值达到限制条件时，可缩短分段点所在的区间，并逐渐逼近分段点，再结合1.2节中提到的在没有油耗数据的区域内进行估计会削弱油耗估计的合理性，要求逼近的分段点位置远离这些区域。

经过实验确定统计分析阈值进而确定分段点的位置，最终建立分段线性估计模型。

3 实例分析

3.1 数据来源

文中的样本数据是源于某航司某机型实飞QAR数据。

航程采用航段大圆距离[11]、油耗采用发动机燃油流量对时间的积分或累加和的结果，取整数有效位数。

3.2 非线性估计

在2.1中阐明了航程与航班油耗之间的非线性关系，并采用多项式函数描述其非线性。前述航司机型全航程各航段油耗分布性态指标结果如表3所示。

从表3中能够看出，该机型其他航段的分布性态均为偏态性，于是，将不同航程的航班油耗量用其对应的中位数来表示。各航段下所取航程油耗的样本集如图6所示。

按照2.2节中给出的多项式拟合的方法，对图3航程与航班油耗进行非线性拟合，得

y=1.304×10-11x4+2.21×10-7x3-

0.001 092x2+7.814x+2 697

(6)

方程拟合优度指标R2=0.998 1，拟合度高，结果是可信的。在一定误差允许范围内，该表达式可作为航班油耗与航程的非线性估计模型，其多项式拟合的结果如图6所示。

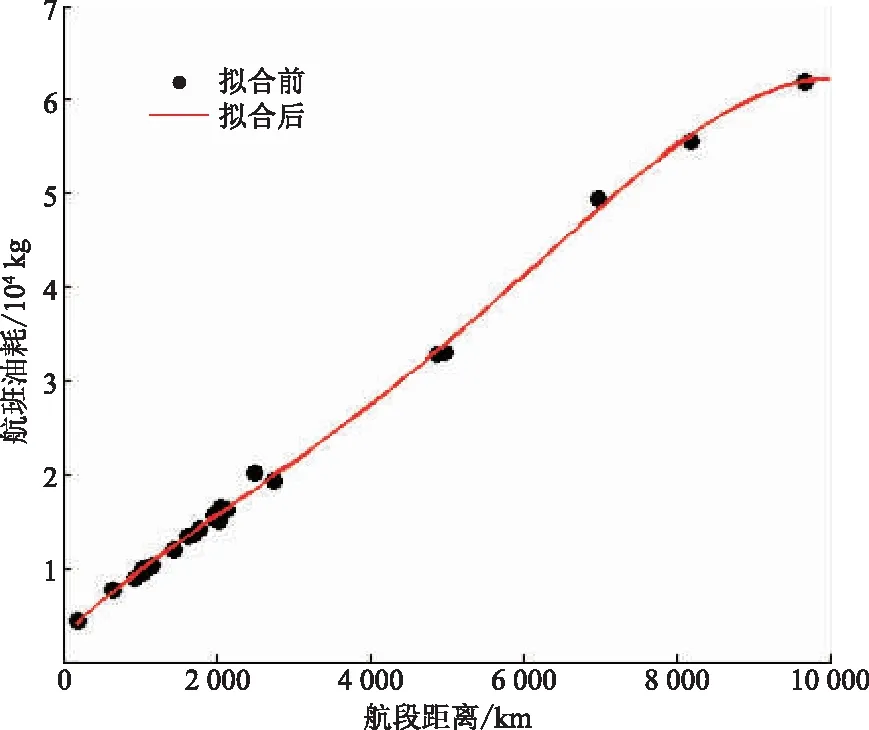
图6 多项式拟合模型显示图Fig.6 Polynomial fitting model display

3.3 分段点的寻找

按照2.3节中给出的非线性的线性化方法，寻找分段点的位置，然后用分段点的位置来区分不同的分段区间，最终构建出分段线性估计模型。首先，以步长100 km为参考，观察航段的导数值的变化规律，由于数据量过多，表格内容仅显示导数值发生变化的区域(下同)，其结果如表4所示。

由拟合结果式(6)，其导数变化如图7所示，考虑公式(5)约束，这里考虑建议的δ1取值范围[0.005，0.05]、δ2取值范围[550，750]。δ1与δ2的取值范围均相差比较大，需要进一步缩小步长来确定。

表3 各航段下所取航程油耗与实际航程油耗 指标对比结果Table 3 Comparison results of fuel consumption index between the range taken under each segment and the actual range

表4 步长为100 km的航段导数值变化区域Table 4 Variation area of segment conductance value with step length of 100 km

接下来，分别以步长50、20、10 km为参考，观察航段的导数值的变化规律，其结果如表5～表7所示。

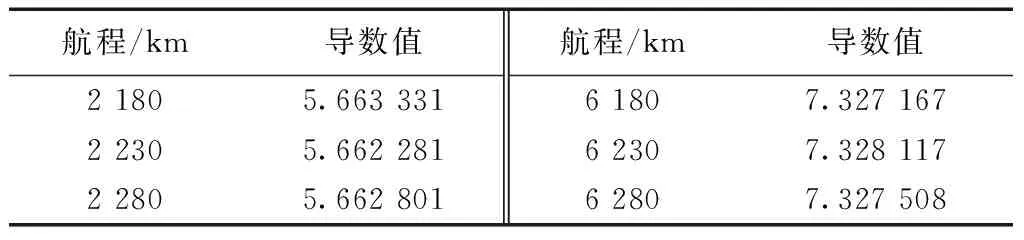
表5 步长为50 km时的航段导数值变化区域Table 5 Variation area of segment conductance value with step length of 50 km

图7 导数值变化Fig.7 Variation of derivative value

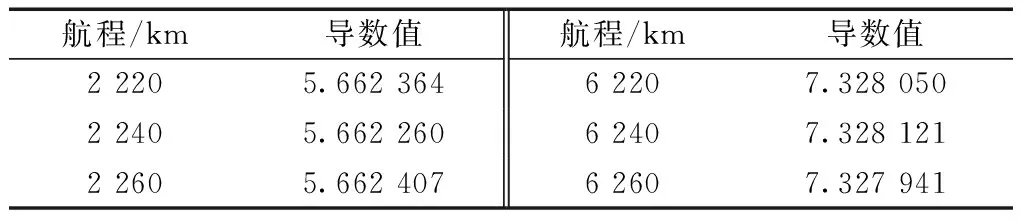
表6 步长为20 km时的航段导数值变化区域Table 6 Variation area of segment conductance value with step length of 20 km

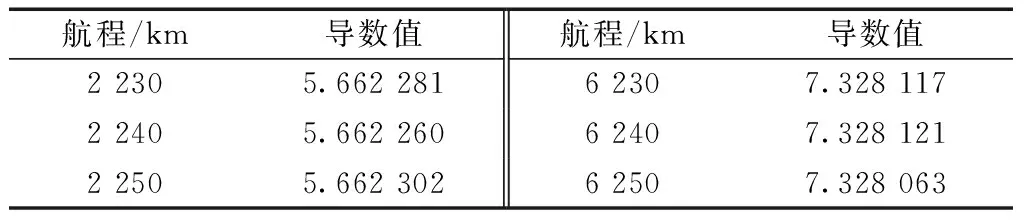
表7 步长为10 km时的航段导数值变化区域Table 7 Variation area of segment conductance value with step length of 10 km

分析表6与表7发现，步长为20 km或10 km时，其导数值的变化规律相同。由拟合结果式(6)，其导数总体变化趋势不变，考虑式(5)约束，这里考虑建议的δ1取值范围[0.000 2,0.002]、δ2取值范围[100，140]。由于在2 200 km与6 000 km左右的区域内没有对应的航班油耗数据，受此限制条件的制约，将分析得到的分段点位置需要进行调整，经过实验测试，最终分段点的位置确定在2 100 km和4 900 km处。考虑步长的因素以及航班油耗数据分布的限制，最终选取的分段点x为180 km(实际最短航程)、2 100 km、4 900 km和9 669 km(实际最大航程)。

3.4 分段线性估计模型

基于统计分析阈值的航段油耗分段线性估计模型如图8所示。

求得该分段估计模型的表达式为

(7)

图8 航段油耗分段线性估计模型Fig.8 Piecewise linear estimation model of fuel consumption in segment

4 结论

构建了一种基于统计分析阈值的航段油耗分段线性估计模型。首先分析航段油耗间存在的复杂非线性特征，不仅在全航程航段油耗表现为非线性，而且单一航段油耗也表现为非线性；其次，对航段油耗做高阶多项式拟合，达成对航段油耗的非线性估计；随后，为降低非线性的复杂程度，将非线性线性化，确定统计阈值，寻找分段区间的分段点，最终建立飞机油耗分段线性估计模型。实例分析结果表明了方法的有效性。