基于CIR模型的欧式外向型障碍期权定价

郑天赐

广西师范大学数学与统计学院 广西桂林 541006

1 绪论

障碍期权是一种终期收益，不仅依赖标的资产在期权到期日的价格，还依赖标的资产在整个期权生命期内达到的某一规定的关卡值的期权合约，该合约能够在一定程度上降低投资者的风险，且比标准期权价格便宜，是一种弱路径依赖型期权。障碍期权定价研究有丰富的成果，例如，胡小平与曹杰、孙玉东等人在标的资产满足Black-Scholes模型研究了障碍期权。

上述研究是基于标的资产价格满足Black-Scholes模型，然而大量实证研究已证实Black-Scholes模型的假设与实际存在诸多不符。例如，市场利率的常数假定，标的资产波动率的常数假定，等等。为此，改进Black-Scholes模型条件成为重要的研究内容之一。其中在Black-Scholes模型中引入市场利率和资产波动率的随机变动过程是重要改进之一。

近年来，在随机利率模型或随机波动率模型下研究亚式期权或障碍期权定价的国内外学者薛广明与邓国和在Bates模型下，给出了离散时间的障碍期权价格的封闭解；ZHONG Y H等人研究了随机利率双Heston随机波动模型下的几何亚式期权定价。这些期权定价的研究均是基于单一资产价格驱动，尤其是障碍期权的收益局限于自身是否触及障碍水平，然而实际中，期权收益不仅依赖自身价格变化，可能受市场其他资产价格的变化或是否触及障碍水平等约束。欧式外向型障碍期权的收益依赖有效期内标的资产的价格平均值以及障碍水平，其中障碍水平由与标的资产相关的另一个资产价格的变动触发，而期权的回报取决于标的资产。由于触发障碍水平分上升敲入/敲出和下降敲入/敲出。于是，本文在CIR随机利率和随机波动率模型下以欧式外向型下降敲出障碍期权为研究对象，开展其定价研究。

2 市场模型

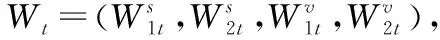
(1)

3 联合特征函数

定理3.1 假设标的资产，满足模型(1)及市场基本假设条件，则特征函数(，，，，，；，，，)具有如下解析表达式:

{++(，，，，)+(，，，，)+(，，，，)}

其中=-，(，)=(+-1)，=0，1，2，

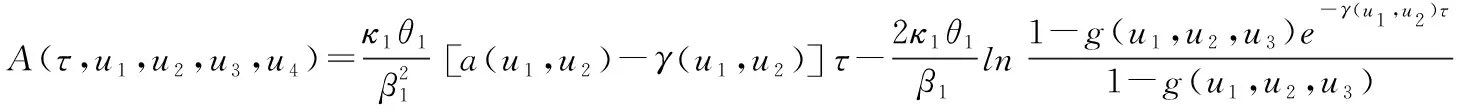
证明：

由Ito公式和Feynman-Kac定理可知，(，，，，，；，，，)≜(，，，，)满足下列偏微分方程(PDE)

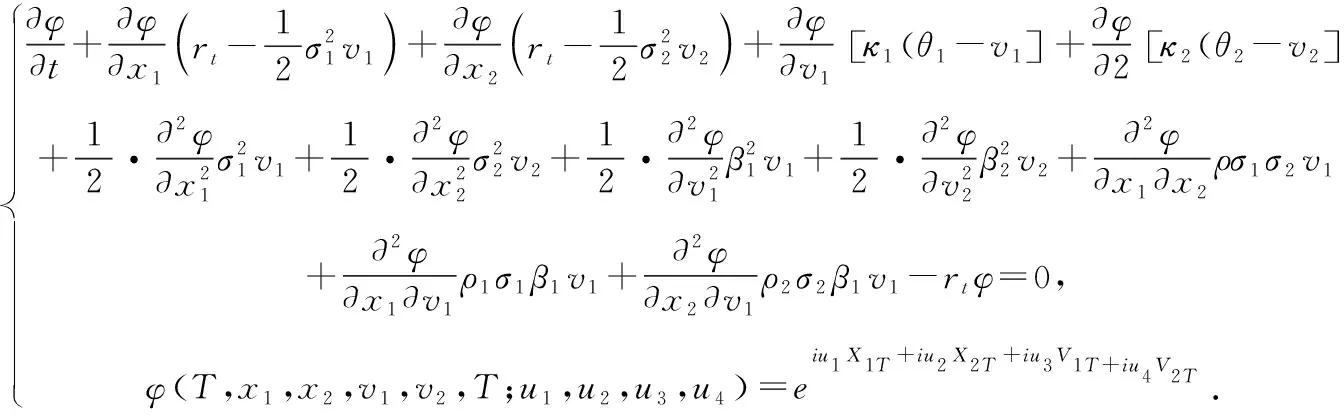
(2)

根据文献[6]知，模型(1)具有仿射结构特征，因此方程(2)的解(，，，，)具有指数形式：

{++(，，，，)+(，，，，)+(，，，，)}

将其代入方程(3)，则：

(3)

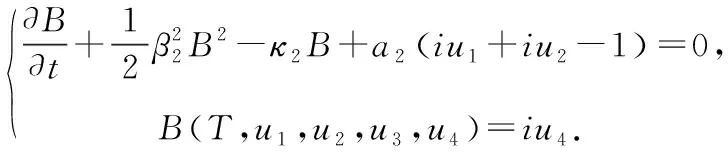
(4)

(5)

显然，方程(3)可改写成:

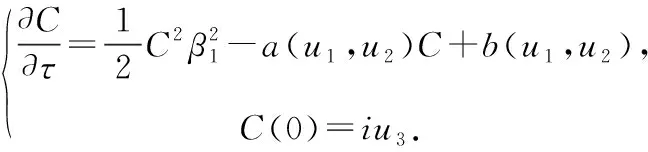
(6)

对于方程(5)，同样在[0，]上进行积分，并把()和()的表达式代入，经过烦琐计算，即得()的表达式。

注令====0，则到期日为T的无风险零息债券t时刻的价格为：

4 定价结果

其中，={，0}，为期权执行价，是障碍水平。

定理4.1：在DSVSI模型下，基于标的资产1，2的欧式外向型下降敲出看涨期权在t时刻的价格为：

(，1，2，)=(-，0)Π-(，)Π

其中:

≜-

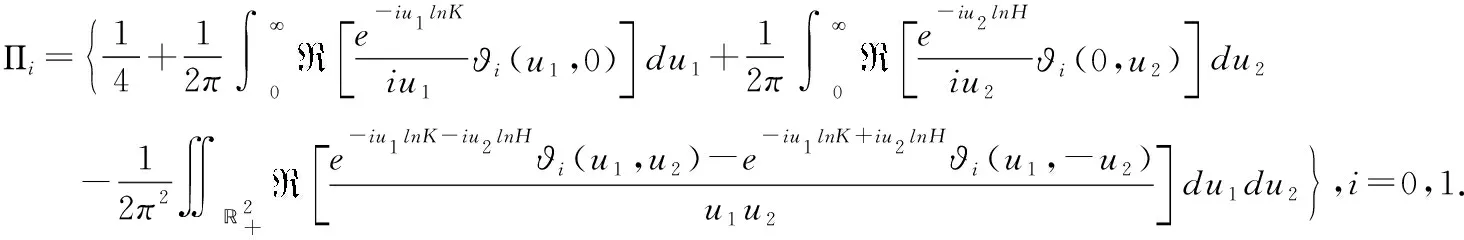
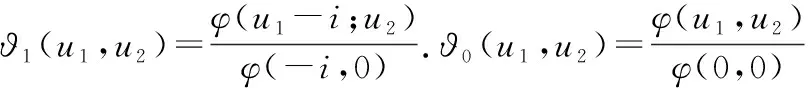
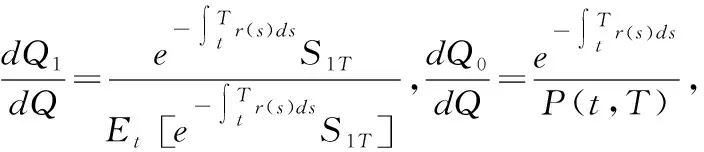
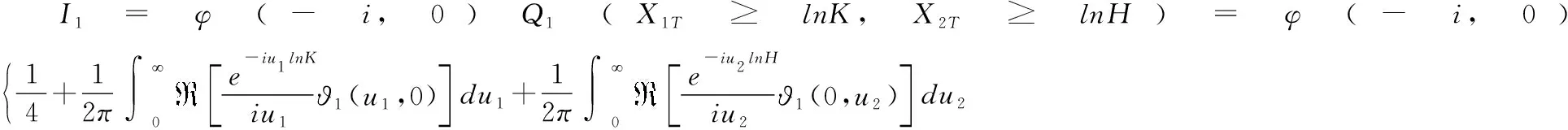
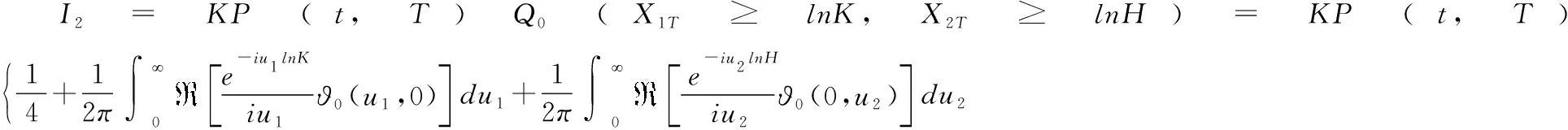
结语

本文在CIR随机利率下研究了标的资产价格满足随机波动率模型的欧式外向型下降敲出看涨期权的定价，将传统的单资产的内向型障碍期权拓展到两资产的外向型障碍期权，并给出了它的定价解析公式。本文研究结果有利于金融衍生品的创新设计及其定价提供新思路和方法，也为市场投资者进行风险管理和投资提供理论依据。