一类广义NLS-MKdV 方程族及其双哈密顿结构
董凤娇, 胡贝贝
(1. 滁州学院计算机与信息工程学院,滁州 239000; 2. 滁州学院数学与金融学院,滁州 239000)
0 引言
在孤子理论中寻找新的可积方程是一个非常重要的研究课题,传统的方法是使用零曲率方程,李代数和利用迹恒等式(变分恒等式),将相应的孤子方程转化为哈密顿形式[1]。最近,很多新的可积系统利用迹恒等式的经典可积方程的推广以及其哈密顿形式被构造出来。例如,广义Ablowitz-Kaup-Newell-Segur(AKNS)孤子族[2]、广义Kaup-Newell(KN)孤子族[3]、广义Wadati-Konno-Ichikawa(WKI)孤子族[4]、广义Dirac 孤子族[5]等。这些广义孤子系统通常都具有双哈密顿结构,这保证了遗传递归算子的存在性与Liouville 可积性[6–8]。
带自相容源的孤子方程在物理学中有着广泛的应用,它涉及流体力学、固体物理和等离子体物理。一般来说,孤子方程的源会导致孤立波变速运动,使孤子的运动特性发生了很大的变化。可积系统自相容源描述了不同孤立波之间的相互作用[9–10]。例如,带自相容源的Kadomtsev-Petviashvili(KP)方程族可以用来描述短波和长波在x–y平面上的相互作用[11],带自相容源的Korteweg-de Vries(KdV)方程族可以用来描述等离子体高频波包与低频波包权重的相互作用[12]。
经典NLS-MKdV 方程的等谱问题是由Guo 在1997 年提出的[13]。2008 年,Zhang 和Dong 在文献[14]中给出了经典NLS-MKdV 方程的哈密顿结构。随后,Chang 和Zhang 在文献[15]中给出了NLS-MKdV 方程的多分量可积耦合结构。此外,关于二元非线性和分数阶超NLS-MKdV 结构也都被学者研究过[16–19]。本文目的是提出一个广义的NLSMKdV 孤子族,构造其双哈密顿结构,并分析其自相容源和守恒律。
本文结构如下:在第1 部分,我们将构造一个基于李代数sl(2,R)的广义NLSMKdV 孤子族;在第2 部分,我们利用变分导数所产生的迹恒等式分析广义NLSMKdV 孤子族,给出其具有Liouville 可积性的双哈密顿结构;在第3 部分,我们构造带自相容源的广义NLS-MKdV 方程族;在第4 部分,我们借助Riccati 方程研究广义NLS-MKdV 方程族的无穷守恒律;最后,我们将给出本文的讨论和总结。
1 广义NLS-MKdV 方程族
我们考虑Lie 代数sl(2,R)的基为

它们满足如下关系

假设Loop Lie 代数G1的基是{e1(n),e2(n),e3(n)|n ∈Z},其中x(n)=x⊗λn。与Lie 代
数sl(2,R)有关的经典NLS-MKdV 谱问题为
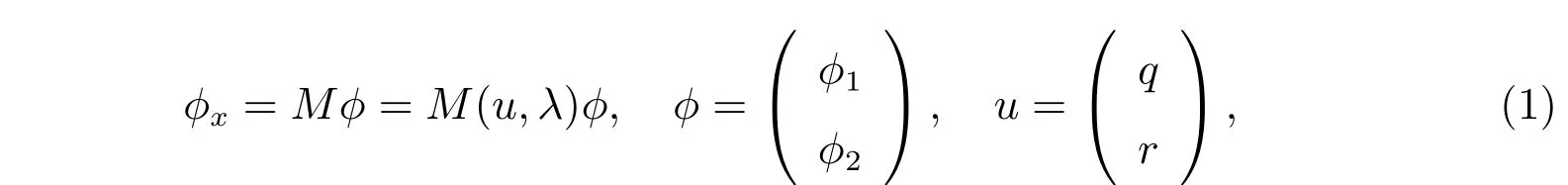
其中
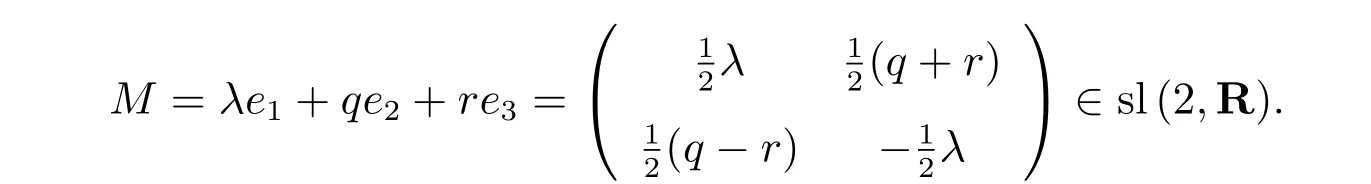
现在,我们引入广义NLS-MKdV 矩阵谱问题

其中h=µ(q2−r2),µ是任意的常数。显然,当µ= 0 时,矩阵谱(1)就约化为标准的NLS-MKdV 矩阵谱[16]。为了得到与矩阵谱(1)对应的孤子方程族,我们首先解静态零曲率方程

其中
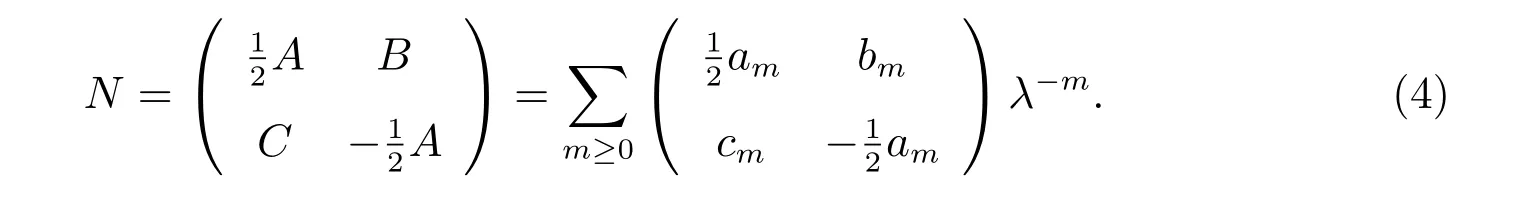
把(2)式定义的M和上述N代入方程(3),并比较λ同次幂的系数得到
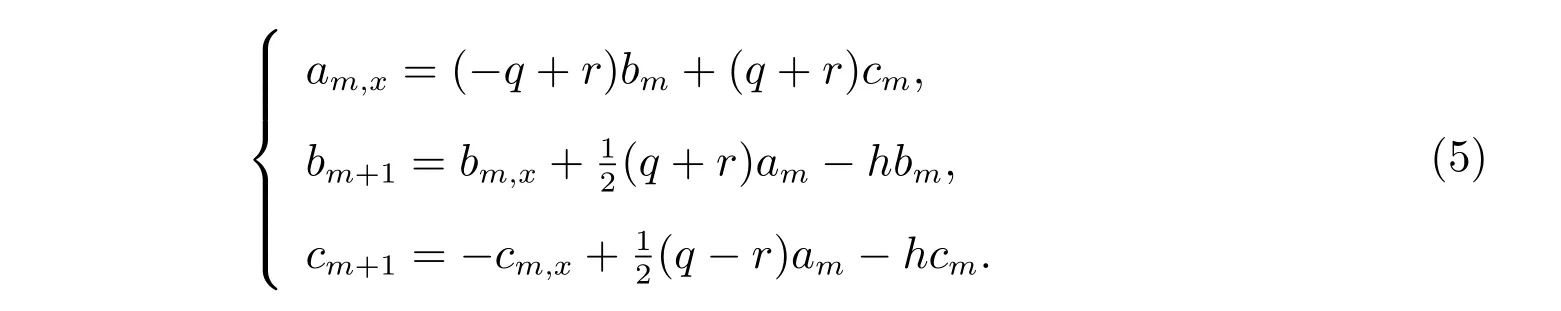
由方程(5)得到递推公式为

其中∂−1∂=1 且递推算子L定义为

我们选取初始值a0= 1,b0=c0= 0,则aj、bj、cj(j ≥1)可以根据方程(6),并借助符号计算软件Maple 唯一算出,我们列出前三项如下
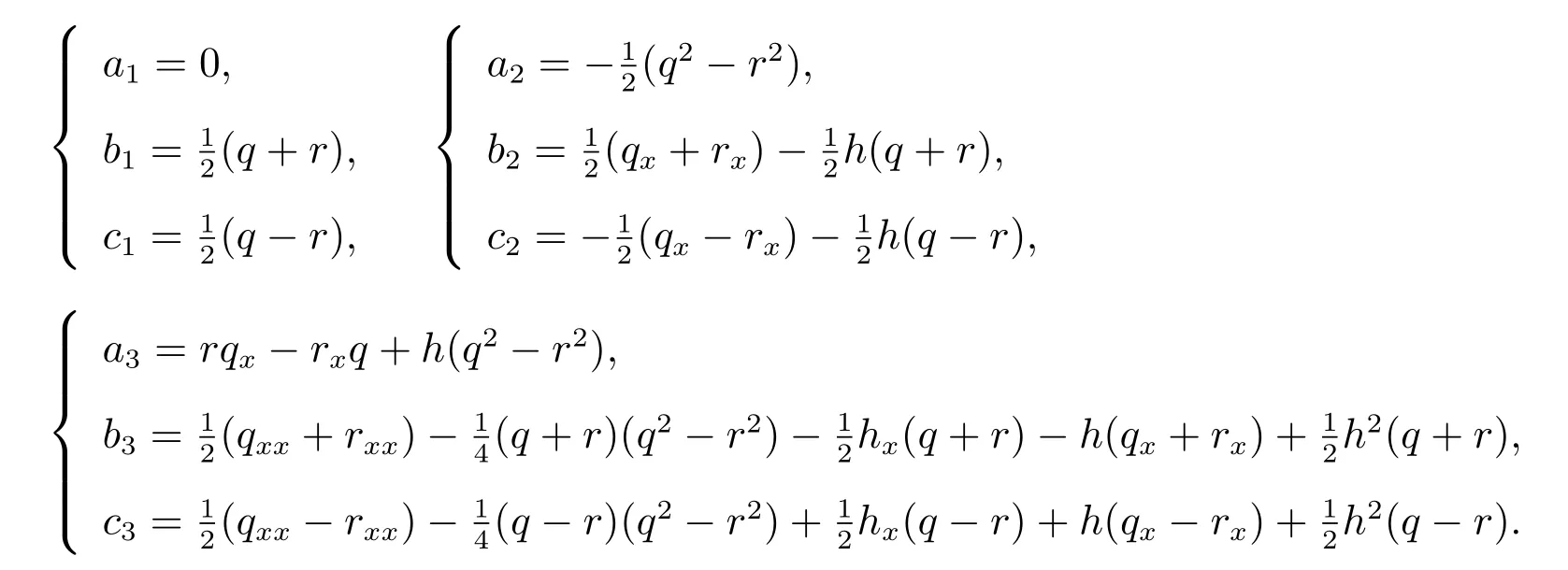
与此同时,我们引入辅助谱ϕtn=N(n)ϕ,其中
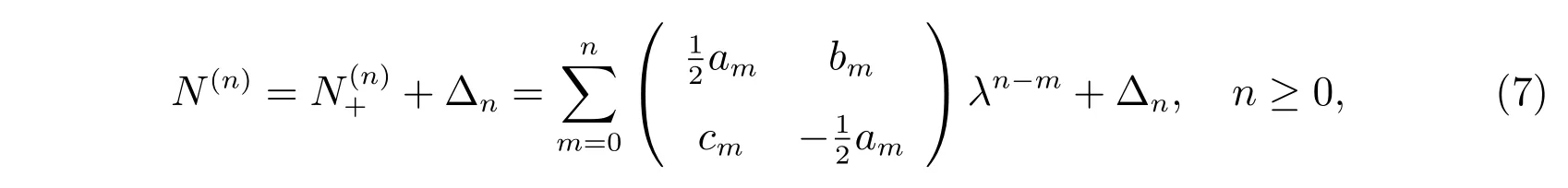
这里∆n为修正项,为了不出现标准的NLS-MKdV 情形,我们假设

并且把方程(1)和方程(7)代入如下的零曲率方程

利用方程(5)得到
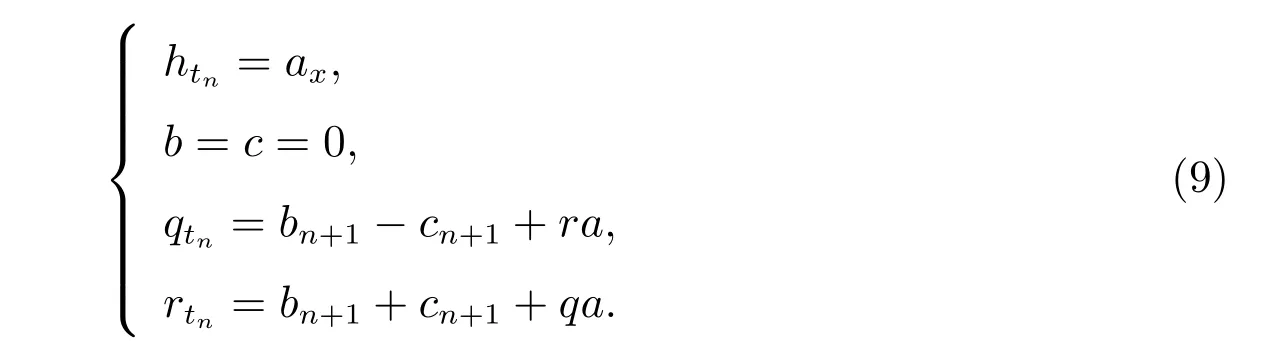
因此,我们有

选取a=−4µan+1,我们得到如下的方程族
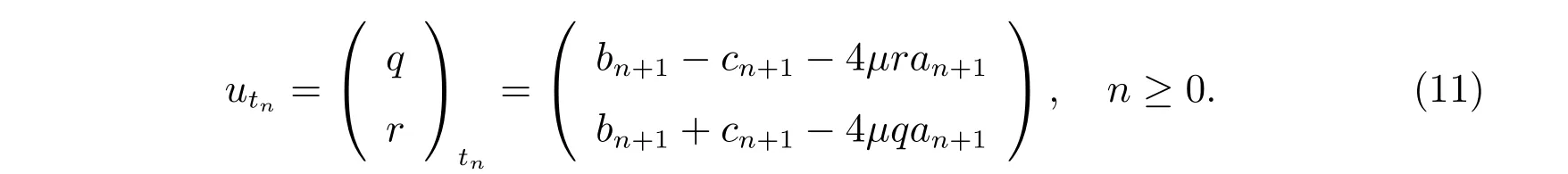
当µ= 0 时,方程(10)就是经典的NLS-MKdV 方程族。因此,方程(11)被称为广义NLS-MKdV 方程族。当n=2 时,所对应的方程为
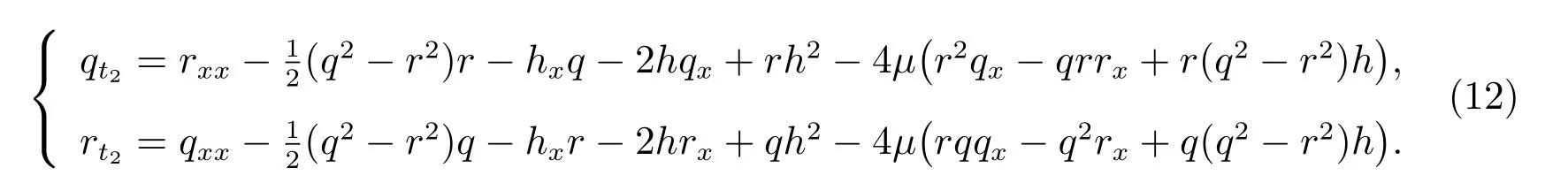
其Lax 对为方程(2)中定义的M和N(2),而N(2)定义如下

当µ=0 且t2=t时,方程(10)可以约化为经典的NLS-MKdV 方程族[16]
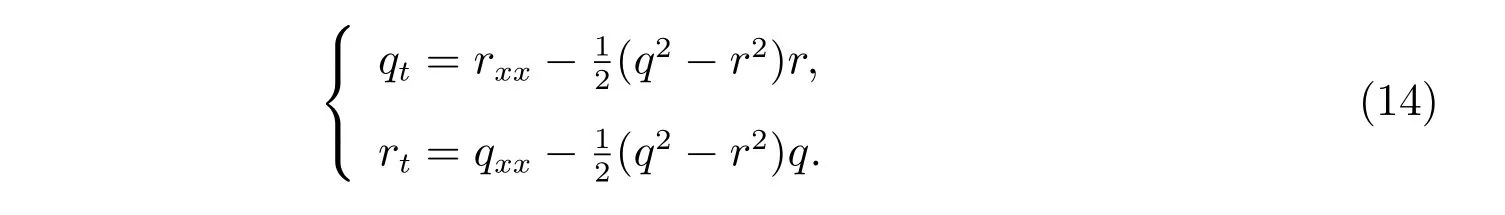
2 双哈密顿结构
在本节中,我们通过如下的迹恒等式来考虑广义NLS-MKdV 方程族的哈密顿结构

其中
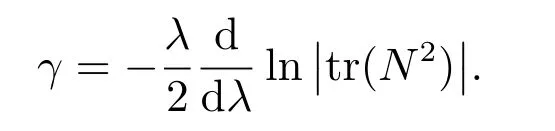
基于上述的迹恒等式,我们有

把方程(16)代入方程(15),比较λ−n−2的系数,得到
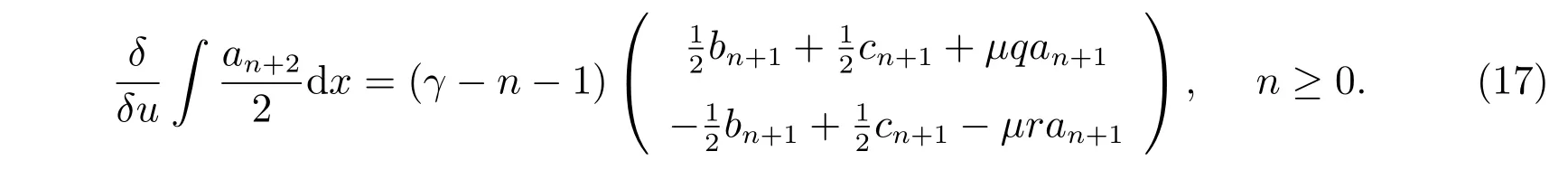
为了确定γ的值,我们令(17)式中的n=0,得到γ=0。因此,我们有
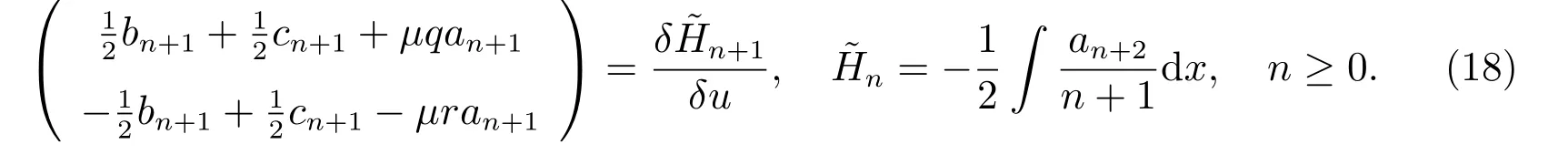
此外,通过直接计算,我们还可以得到

其中R定义如下
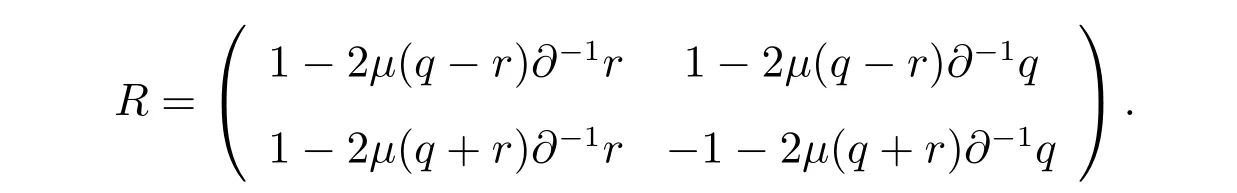
一方面,广义NLS-MKdV 方程族(10)有如下的哈密顿结构
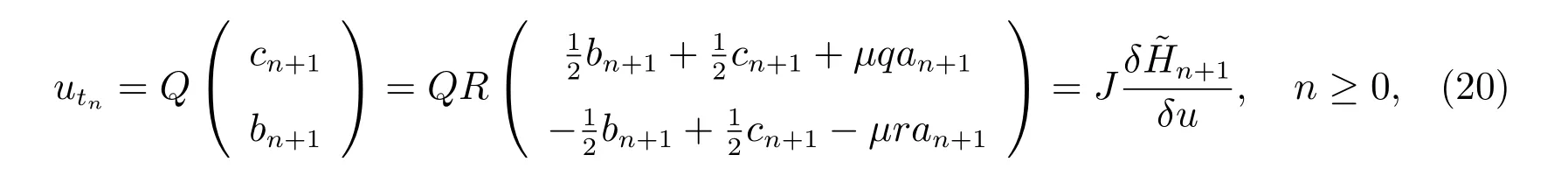
其中
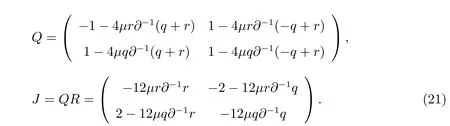
我们可以证明J为哈密顿算子。
另一方面,我们由递推关系(6)得到广义NLS-MKdV 方程族有如下的双哈密顿结构

其中P=QLR=(Pij)2×2表示为
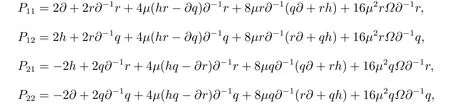
这里Ω=∂−1r∂r −∂−1q∂q,并且我们可以证明P为第二个相容哈密顿算子。
3 自相容源
这一节,我们将构造带自相容源的广义NLS-MKdV 方程族,在谱问题

中,令λ=λj,相应的谱向量ϕ记为ϕj,则得到N个相应的线性问题如下
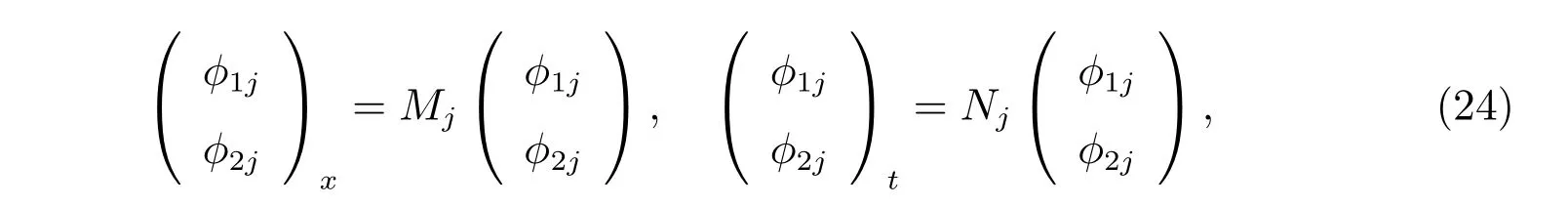
其中Mj=M|λ=λj,Nj=N|λ=λj,j=1,2,···,N。我们还得到
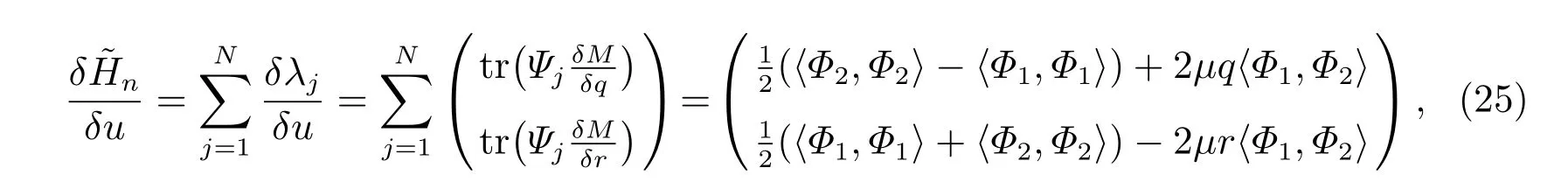
其中Φj=(ϕj1,ϕj2,···,ϕjN)T,j=1,2,3,故带自相容源的广义NLS-MKdV 方程族为

其中J为方程(21)定义的哈密顿算子。
4 守恒律
在这一节中,我们将要构建广义NLS-MKdV 方程族的守恒定律。引入变量如下

于是
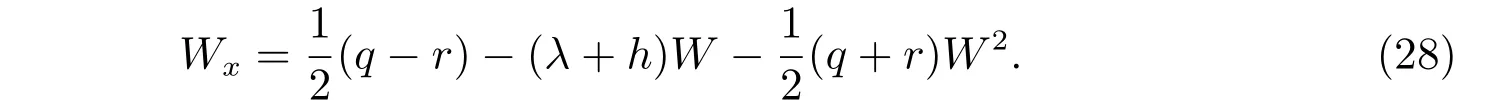
假设

把方程(29)代入方程(28),并且比较λ同次幂系数,得到{wn+1}的递归公式为
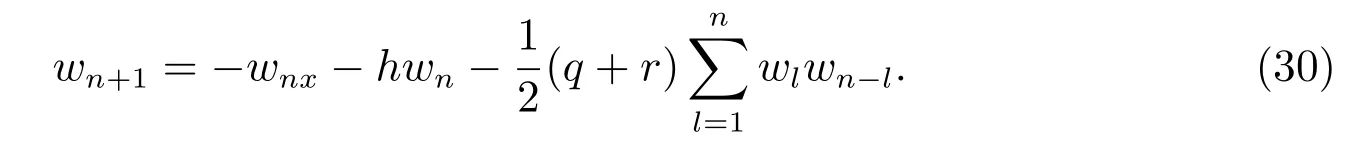
由方程(23)可以得出
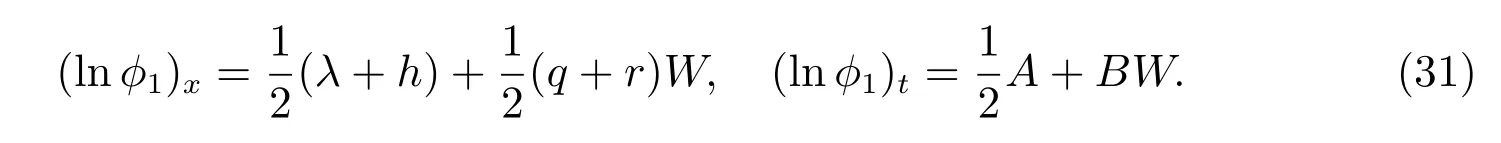
因此,我们有
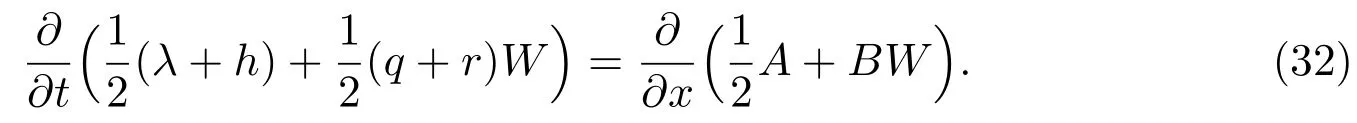
令
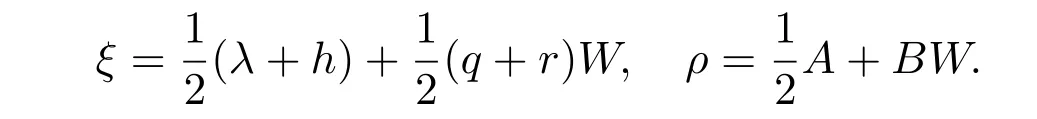
于是,方程(32)等价于ξt=ρx,这正好是n=2 时的守恒定律的标准定义

假设
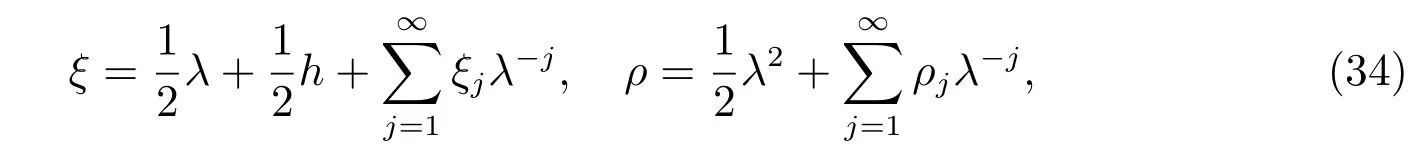
则第一个密度流和守恒量为
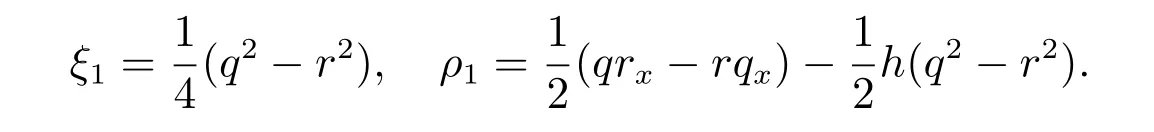
由方程(32)∼(34),得出ξn和ρn的递归关系如下
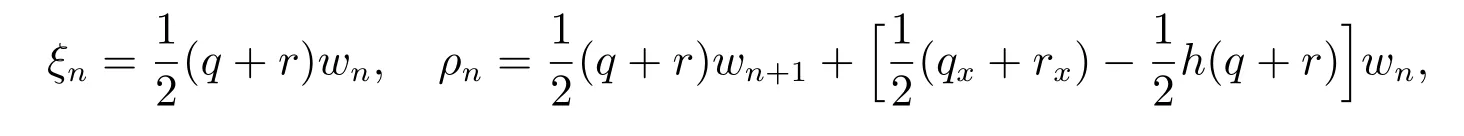
其中wn由方程(30)定义。
5 结束语
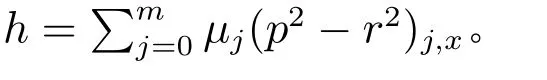
事实上,我们还可以在Lie 代数so(3,R)上,考虑利用下面的空间矩阵谱问题来构造更一般的广义NLS-MKdV 孤子族[6–8]
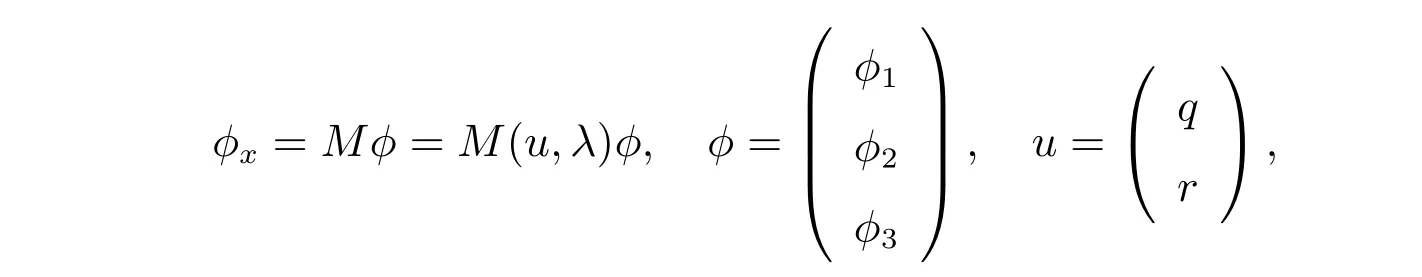
其中

我们还可以将费米子奇变量α和β引入广义NLS-MKdV 孤子方程族,并将广义NLS-MKdV 族扩展到超广义NLS-MKdV 孤子族。其中,费米子奇变量α和β满足关系为αβ=−βα和α2=β2=0,这些问题将在我们以后的工作中进行讨论。

