货车转向架相对摩擦因数设计值和试验结果差异分析

刘振明

(中车齐齐哈尔车辆有限公司 大连研发中心，辽宁 大连 116052)

弹簧减振装置是铁路货车转向架的重要部件，相对摩擦因数是其关键参数，直接影响车辆动力学性能[1-2]。多年实践表明，实测相对摩擦因数往往和设计值存在一定差异。本文将对两者之间的差异原因进行分析，定量地给出差异程度，并给出协调两者的具体建议。

1 摩擦楔块式减振器结构和作用原理

铁路货车铸钢三大件式转向架一般采用摩擦楔块式减振器，可分为变摩擦和常摩擦2种结构(图1)，2种减振器的楔块受力分析如图2、图3所示。

图1 摩擦楔块式减振器结构

图2 变摩擦减振器楔块受力分析

图3 常摩擦减振器楔块受力分析

2 相对摩擦因数定义计算方法及特性

2.1 相对摩擦因数定义[3-4]

楔块式减振器阻尼的大小通常用相对摩擦因数φ来表示，它是摩擦力与垂向力的比值(以下简称“定义力比法”)，一般只用主摩擦面上的摩擦力来计算(副摩擦面的摩擦功占比很小，略去不计)，即：

(1)

式中：Fu——楔块向上运动时，一个楔块主摩擦面的摩擦力；

Fl——楔块向下运动时，一个楔块主摩擦面的摩擦力；

P——摇枕每端弹簧垂向反力总和。

2.2 定义力比法计算相对摩擦因数

2.2.1 变摩擦减振器(减振簧与枕簧等高)

对于变摩擦减振器(图2)，式(1)中的P为：

P=nKz+2Pa

(2)

式中：n——摇枕每端枕簧组数；

K——每组枕簧的垂向刚度；

z——摇枕垂向位移，即枕簧挠度；

Pa——一个楔块上的弹簧垂向反力。

Fu、Fl可用以下公式表示：

(3)

(4)

其中：

Δu=(1+μμ1)cos(α-β)-(μ1-μ)sin(α-β)

(5)

Δl=(1+μμ1)cos(α-β)+(μ1-μ)sin(α-β)

(6)

式中：μ——主摩擦面摩擦因数；

μ1——副摩擦面摩擦因数；

α——楔块副摩擦面与水平面夹角；

β——楔块主摩擦面与垂直面夹角；

K1——减振簧垂向刚度；

z1——楔块垂向位移。

由式(1)可知，按定义力比法得出的φ是根据某一给定弹簧挠度下各力计算得出的数值，当减振簧与枕簧等高时，楔块下移量就是减振簧压缩量，可得：

(7)

(8)

可见，φ仅与K、K1、α、β、μ、μ1有关。如果此时K=K1，则式(7)可简化为：

(9)

此时φ为定值，无论枕簧挠度多大，φ都相同。

以转8A型转向架为例，代入各参数后求得其P、Fu、Fl、φ与枕簧挠度的关系如图4、图5所示。

图4 P、Fu、Fl与枕簧挠度的关系

图5 φ与枕簧挠度的关系

2.2.2 变摩擦减振器(减振簧加高)

为了缓解楔块磨耗后上升、减振簧压缩量变小导致的减振力不足，设计时一般使减振簧高度大于枕簧高度[5-6]。当减振簧加高时，得到：

(10)

式中：h——减振簧比枕簧高出值。

可见，φ不仅与K、K1、α、β、μ、μ1有关，还与h、z1有关，h为常数，z1可用z的函数表达，而z是变量，因此φ是一个随z变化的值，即相对摩擦因数与弹簧挠度有关。

以转K2型转向架为例，代入各参数后求得其P、Fu、Fl、φ与减振簧挠度的关系如图6、图7所示。

图6 P、Fu、Fl与减振簧挠度的关系

图7 φ与减振簧挠度的关系

2.2.3 常摩擦减振器

常摩擦减振器的楔块受力中，主摩擦面为垂直面(图3)。因结构不同，计算其相对摩擦因数时，摇枕每端弹簧垂向反力总和不再含有楔块上的减振簧反力[7-8]。通过受力分析(因主摩擦面为垂直面，因此假设斜楔斜面与摇枕斜楔槽斜面间无相对运动趋势，即图3中斜面上的F1u=0、F1l=0)，求得Fu、Fl可用以下公式表示：

(11)

(12)

式中：f——减振簧垂向压缩量，常数；

γ——楔块副摩擦面与主摩擦面夹角。

将P、Fu、Fl代入式(1)，得：

(13)

由式(1)及式(13)可知，常摩擦减振器的φ与K、K1、γ、μ、μ1、n、f、z有关，因为z是变量，其余为常数，因而随着枕簧挠度的不同，φ也随之变化；z变大时，φ变小。

以转D21型转向架为例，代入各参数后求得其P、Fu、Fl、φ与枕内簧挠度(内簧高于外簧)的关系如图8、图9所示。

图8 P、Fu、Fl与枕内簧挠度的关系

图9 φ与枕内簧挠度的关系

3 标准测定方法与定义力比法的差异

3.1 标准测定方法

GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》附录A规定，相对摩擦因数测定方法是：“试验时对转向架心盘平稳地逐级施加垂向载荷，加至最大试验载荷后，再平稳地逐级减载至零位。最大试验载荷不应小于转向架簧上静载荷”，加载曲线如图10所示。

图10 加载曲线

相应的相对摩擦因数φ1计算方法为[9]：

(14)

对比式(14)与式(1)可知，式(1)采用某一给定弹簧挠度时瞬时力比值计算理论相对摩擦因数，而图10和式(14)采用载荷从零到某一给定心盘载荷时加减载曲线所围成的各面积比值计算(以下简称“试验面积比法”)。由于方法不同，两者将在理论上产生计算结果差异。

3.2 试验面积比法计算相对摩擦因数

3.2.1 变摩擦减振器(减振簧与枕簧等高)

对于变摩擦减振器，当减振簧与枕簧等高时，理想加载曲线如图11所示，即A点与O点重合，各面积均为三角形[10]，将三角形面积计算公式代入式(14)，得：

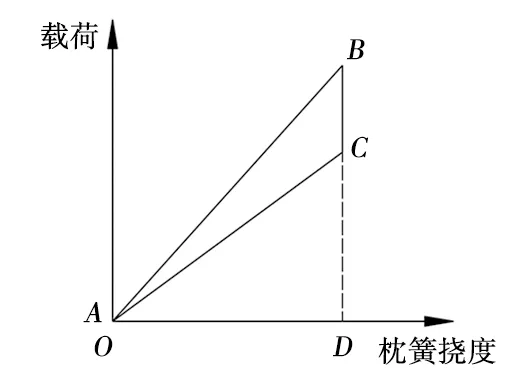
图11 理想加载曲线

(15)

(16)

(17)

对比式(17)与式(1)可知，按定义力比法计算φ值时分母为弹簧垂向反力P，不包含摩擦力Fu、Fl，而按试验面积比法计算φ1值时，分母包含了摩擦力Fu、Fl。根据式(3)、式(4)可知，Flφ。

以转8A型转向架为例，φ1是φ的1.033倍，如图12所示。

图12 φ1/φ与枕簧挠度的关系

3.2.2 变摩擦减振器(减振簧加高)

图13 减振簧加高时的加载曲线

按试验面积比法进行计算，可得：

(18)

将三角形、梯形面积计算公式代入，得：

(19)

(20)

(21)

可见，式(21)与式(17)很相似，但增加了减振器结构参数h和摇枕位移z，根据上述分析，此时如果还按式(17)计算，则计算出的φ1其实是图13(a)中加载曲线为AB、AC时的值，反映不出G、E点对面积比的影响，所以会产生误差。

与3.2.1同理，式(21)与式(1)的分子分母均不同，由于较复杂，不能直接判断出φ1与φ的大小，必须按实际参数计算。

如果减振簧为一级刚度、枕簧为二级刚度，则试验加载曲线如图13(b)所示的实线图形，即AGKBCHE，这时如果加载枕簧挠度位于FJ间，则φ1的求解公式类似式(21)。如果位于JD间，则可用试验面积比法按同样的过程推导出φ1的求解公式如下：

(22)

式中：Px——减振簧压缩h时摇枕一端的弹簧垂向反力；

Fyu——第1级枕簧(高枕簧)压缩h1、楔块向上运动时一个楔块主摩擦面的摩擦力；

Fyl——第1级枕簧压缩h1、楔块向下运动时一个楔块主摩擦面的摩擦力；

Py——第1级枕簧压缩h1时摇枕一端的弹簧垂向反力；

z2——以第2级枕簧(矮枕簧)计算的压缩量；

h1——两级枕簧高度差。

以符合上述情况的转K2型转向架为例，φ1是φ的1.75倍(空车)和1.44倍(重车)，其随减振簧挠度的变化趋势如图14所示。

图14 φ1/φ与减振簧挠度的关系

转K2型转向架按试验力比法公式(17)求得的φ2是φ的1.059倍(空车)和1.025倍(重车)，其随减振簧挠度的变化趋势如图15所示。

图15 φ2/φ与减振簧挠度的关系

3.2.3 常摩擦减振器

对于常摩擦减振器，如图16(a)所示，最初从平衡位置O点加载，由于存在一个常摩擦力，因此先到A点，期间枕簧挠度不变，然后至B点，减载时沿BCF至载荷为0的F点。由于常摩擦力的存在，枕簧挠度不能回到平衡位置O点，而是止于F点，再次加载、减载则沿FEBC循环进行，AE段仅第1次加载时经过，因Fu、Fl为常数，故FEBC为平行四边形。

图16 常摩擦减振器加载曲线

考虑到一般测试要循环几次，所以应忽略第1次加载的AE段，此时按试验面积比法计算，可得：

(23)

按图16(a)，将三角形、梯形、平行四边形面积计算公式代入，得：

(24)

(25)

(26)

化简得：

(27)

对比式(27)与式(1)可知，当Fl=P/2时，式(27)可化简为式(1)，两者等效；当Fl

如果枕簧为二级刚度，则试验加载曲线为图16(b)所示的实线图形，即FEKBCM，这时如果加载枕簧挠度位于FJ间，则φ1的求解公式类似式(27)。如果位于JD间，则可用试验面积比法按同样的过程推导出φ1的求解公式如下：

(28)

以符合上述情况的转D21型转向架为例，φ1是φ的2.11倍(空车)和2.19倍(重车)，其随枕内簧挠度的变化趋势如图17所示。

图17 φ1/φ与枕内簧挠度的关系

转D21型转向架按试验力比法公式(17)求得的φ2是φ的0.912倍(空车)和0.979倍(重车)，其随减振簧挠度的变化趋势如图18所示。

图18 φ2/φ与枕内簧挠度的关系

4 建议

为了使测试结果可用，避免试验和设计之间由于方法不同导致差异，建议采用如下2种方式进行相对摩擦因数的测试和计算：

(1) 按试验面积比法测试并计算出相对摩擦因数后，利用本文所给出的公式，求出试验面积比法与定义力比法之间的关系，反算出按定义力比法的数值并与设计值对比；

(2) 按试验力比法计算相对摩擦因数，利用本文所给出的公式，求出试验力比法与定义力比法之间的关系，反算出按定义力比法的数值并与设计值对比。