基于动力吸振器的EMS型磁浮车辆-轨道梁耦合振动抑制方法研究

周 阳，胡俊雄，陈晓昊，马卫华，罗世辉

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

自20世纪60年代开始，德国、日本等国相继开展了磁悬浮列车的技术研究。当前国际上已形成较成熟的常导电磁型和低温超导磁悬浮交通技术体系。德国TR(Transrapid)是最具代表性的高速常导磁浮车辆系统，至今共研发了9代车型。目前，已有日本东部丘陵线(TKL线)、韩国仁川机场线、中国长沙磁浮机场线及北京磁浮S1线实现商业运营[1-2]。

EMS型磁浮车辆采用电磁主动悬浮，本质上是不稳定的，并且由于EMS型磁浮列车多采用高架线路运行，轨道梁发生弹性变形时易诱发特殊的车-轨耦合振动现象。国内外学者针对车轨耦合振动问题进行了大量的研究。20世纪70至90年代，Wilson、Cai等[3-4]建立了只考虑沉浮运动的车辆模型，并将电磁力等效为弹簧阻尼器，研究分析了不同车速以及不同梁型的耦合响应；Yau等[5]建立了由车载PI控制器控制的双自由度磁浮车辆与柔性轨道耦合的动力学模型，并提出了新的迭代计算方法，研究分析了车速、磁浮列车垂向加速度对耦合振动的影响；Lee等[6]建立了5自由度的主动控制磁浮车辆-柔性轨道的垂向动力学模型，采用数值分析的方法分析了轨道不平顺、车速、轨道梁跨距等参数对悬浮稳定性的影响；高精隆等[7]分析了吸振器的质量以及阻尼对系统振动的影响，建立了多种数学模型的运动方程，研究了在有无动静质量时系统的减振效果；殷永康等[8]按照目前的技术原理、刚度调整范围以及对应的速度等性能进行了分析和比较，最后提出一种采用锥螺旋弹簧的变刚度的半主动吸振结构；李晓龙等[9]提出了通过设置非线性饱和环节、动态调整饱和阈值来抑制车轨耦合振动的新方法，系统在平衡点附近时通过调整饱和阈值来改变控制输出的幅值特性，逐步消除引起共振的能量，从而达到抑制振动的目的；汪科任等[10]采用AHP(层次分析法)求取系统二次型性能指标中状态加权矩阵的权重系数，建立了2种状态反馈控制器，为悬浮控制器的优化设计提供一定的参考。

本文主要采用动力吸振器作为车-轨耦合振动的制振措施。动力吸振器(Dynamic Vibration Absorber)由辅助质量、弹簧以及阻尼组成，属于抑制共振的被动式制振器，又称调谐质量阻尼器TMD(Tuned Mass Damper)。其基本原理是在振动对象以外建立一个附加的动力学系统，将制振对象的振动响应吸收并消耗在阻尼元素中。动力吸振器在各个工程领域中运用广泛，国内外学者也做了很多研究。刘海平等[11]利用欧拉屈曲梁作为弹簧元件，采用复变量平均法，求解了不同类型非线性吸振器模型的解析解。赵艳影和徐鉴[12]对两自由度系统采用多尺度法研究了时滞非线性动力吸振器对主系统的减振性能，得到了主系统的振幅-时滞响应曲线。研究结果表明，对时滞非线性动力吸振器，可以通过调节反馈增益系数和时滞控制主系统的振动。李俊等[13]将简谐激振下无阻尼单自由度主系统的动力消振原理推广到多频谐波激励下无阻尼多自由度主系统的情况。

本文以某中低速空簧中置式磁浮列车为研究对象，建立了8自由度的车-轨耦合垂向动力学模型，采用基于位移-速度-加速度反馈的PID主动控制，基于扩展定点理论与频率传递函数分析单动力吸振器和多重动力吸振器方案的最佳参数，进而对不同质量比的动力吸振器进行动力学仿真对比。在研究单自由度系统和多模态系统动力吸振器的最佳参数的基础上，分析不同速度下2种减振措施的制振效果。

1 动力学建模

1.1 磁浮车辆模型

某中低速磁浮列车每节车体通过6个空气弹簧支撑在3个悬浮架上，空气弹簧安装于纵梁中间位置。悬浮电磁铁由内外极板以及线圈、铁芯组成，2个线圈为一组，再通过间隙传感器和悬浮控制器构成一套闭环控制系统，一般称之为一个控制单元或控制点，建模过程将单个悬浮架的悬浮力集中在悬浮架前后端点处。本文主要分析磁浮车辆-悬浮控制-轨道梁-动力吸振器系统的垂向动力学响应，因此将车辆简化为由车体、悬浮架组成的刚体系统，仅考虑车体和悬浮架的垂向和点头运动自由度，建立的8自由度的磁浮车辆垂向动力学模型如图1所示。

图1 磁浮车辆垂向动力学模型

磁浮车辆垂向动力学方程如式(1)～式(8)所示。

车体沉浮运动：

(1)

式中：M——车体质量；

z0——车体垂向位移；

k——二系悬挂刚度；

c——二系悬挂阻尼；

z1，z2，z3——悬浮架1，2，3的垂向位移。

车体点头运动：

(2)

式中：J——车体转动惯量；

θ0——车体角位移；

s0——车体半长；

s1——悬浮架半长。

悬浮架1沉浮运动：

(3)

悬浮架1点头运动：

(4)

悬浮架2沉浮运动：

(5)

悬浮架2点头运动：

(6)

悬浮架3沉浮运动：

(7)

悬浮架3点头运动：

(8)

式中：J1，J2，J3——悬浮架1，2，3的转动惯量；

F11～F16——悬浮架对应的悬浮力。

1.2 无动力吸振器(TMD)时轨道梁模型

中低速磁浮交通轨道梁大多为简支梁，本文采用只考虑梁弯曲变形、不考虑剪切变形及转动惯量影响的欧拉-伯努利梁(Euler-Bernoulli beam)模拟轨道梁。动力学模型建立在以下假设条件的基础上：(1)忽略梁的结构阻尼；(2)仅考虑轨道梁在垂向上的受力及动力作用情况；(3)轨道梁为等截面梁，且材质均匀；(4)轨道梁的运动满足小变形理论并在弹性范围内。轨道梁的振动微分方程为：

(9)

式中：E——轨道梁弹性模量；

I——横截面的截面惯性矩；

EI——轨道梁抗弯刚度；

ρ——轨道梁线密度；

Q——轨道梁的外作用力；

x——外力作用位置。

利用模态叠加法，将轨道梁的位移分解为i阶模态下的广义坐标与形函数的乘积：

(10)

式中：φi(x)——轨道梁的i阶振型函数；

qi(t)——轨道梁的i阶模态坐标。

将式(10)代入式(9)中得：

(11)

将式(11)两边同时乘以φn(x)，并沿轨道梁全长进行积分：

(12)

由于主振型的正交性，当i≠n时，方程(12)左侧两项均为0，因此方程(12)可简化为：

(13)

由简支梁的边界条件可求得振型函数：

(14)

由于本文主要研究单跨简支梁的1阶振动影响，代入式(14)整理可得简支梁受迫振动的响应结果：

(15)

式中：Pj(t)——第j个电磁力的大小；

xj是——第j个电磁力的位置；

L——轨道梁跨距；

1.3 有动力吸振器(TMD)时轨道梁模型

图2为带TMD的轨道梁模型。

图2 带TMD的轨道梁模型

由式(14)可知，只考虑轨道梁的1阶振动时最大变形位置为跨中处，所以选择在跨中设置TMD，则TMD的运动方程为：

(16)

将式(10)、式(14)代入可得：

(17)

式中：mt——TMD质量；

kt——弹簧刚度；

ct——阻尼系数；

zt——垂向位移。

此时轨道梁的运动方程为：

(18)

1.4 轨道不平顺

国内外对线路不平顺研究较多，但并不统一，本文采用文献[14]中拟合的磁浮高低线路不平顺功率谱，其数学表达式为：

(19)

式中：Ω——空间频率，m-1；

A，B，C，D，E，F，G——特征参数。

特征参数具体值如下：

A=0.003 782，B=-0.087 513，C=0.001 952，D=-0.213 341，E=0.017 071，F=-0.000 607，G=8.074 24×10-6。

采用三角级数法进行轨道谱反演，得到的磁浮轨道垂向不平顺时域图如图3所示。

图3 磁浮轨道高低不平顺时域图

1.5 悬浮控制模型

本文采用基于位移-速度-加速度反馈的PID主动控制，状态观测器如图4所示。

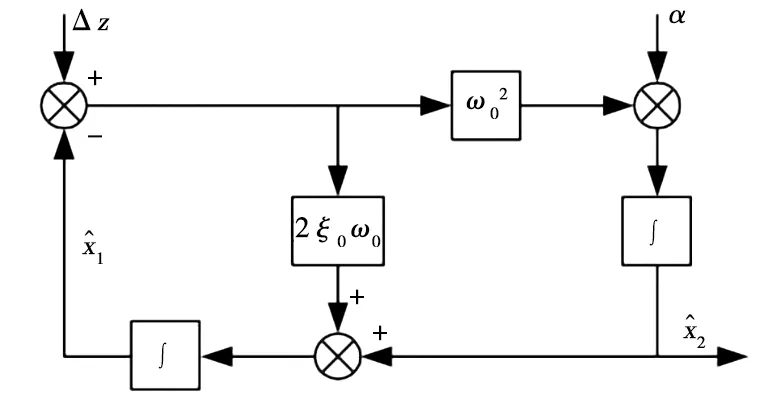
ω0.观测器的特征频率；ξ0.观测器的阻尼。图4 状态观测器

控制器中位移和加速度直接反馈，速度则通过观测器中加速度与位移信号构造而成。控制器电流方程：

(20)

式中：KP、Kv、Ka——分别为PID中位移、速度、加速度反馈系数；

Δz——悬浮间隙位移变化值；

当悬浮间隙在额定间隙处小范围波动时，悬浮力公式为：

(21)

式中：μ0——真空磁导率；

A——磁极面积；

N——线圈匝数；

i0，c0——额定悬浮电流和额定悬浮间隙。

将式(20)代入式(21)即可得实际作用悬浮力：

(22)

2 动力吸振器设计

2.1 单动力吸振器设计

由于动力吸振器的阻尼系数要比轨道梁结构阻尼对轨道梁动力响应的影响大，所以忽略轨道梁的结构阻尼，针对轨道梁1阶模态进行制振，此时轨道梁系统近似为无阻尼单自由度系统。动力吸振器与轨道梁等效系统如图5所示。

图5 动力吸振器与轨道梁等效系统φ1(ω)=arctan

将轨道梁上外力改写为Fejωt，求解方程可得轨道梁和动力吸振器的振幅比与相位：

(23)

(24)

式中：μ——质量比，μ=mt/ρL；

ξ——阻尼比，ξ=c/(2mω1)；

Xst——轨道梁静变形，Xst=F/Kd；

λ——强迫振动频率比；

γ——固有角频率比。

对式(23)两边取平方，并将ξ前系数化为1，则：

(25)

当ξ=0时，振幅比为：

(26)

当ξ=∞时，振幅比为：

(27)

当式(26)等于式(27)时，式(25)与ξ无关，此时式(25)化简为：

(28)

此时式(27)与式(28)相同，振幅比与ξ无关的点就是ξ=0与ξ=∞ 2条曲线的交点，如图6所示。因此可以利用定点现象进行动力吸振器参数设计。

图6 不同阻尼比下振幅比曲线

利用扩展定点理论可以得到动力吸振器最优参数的2个条件：

最优同调条件(2个定点等高)：

(29)

最优阻尼条件(定点处最大阻尼)：

(30)

满足这2个条件后，主振动系统的最大振幅比：

(31)

将式(29)、式(30)代入式(23)中得：

(32)

由式(32)可知，动力吸振器的设计目标简化为对质量比单参数的选择,具体关系如图7所示。

图7 振幅比与质量比的关系

阻尼与频率按照上述公式选取，当外部激励频率与主振动系统的固有频率接近时，振幅比增大；振幅比最大值随着质量比的增大而衰减，可见增大质量比可以提高抑振效果，但是过大的质量比会使得整体系统过重，从而使得轨道梁静挠度增大，所以本文将质量比限制在0.2以下。

根据上述条件，针对轨道梁1阶振动，可以得到动力吸振器3个参数的设计公式：

(33)

2.2 多重动力吸振器设计

考虑轨道梁第i阶模态，针对第i阶模态的轨道梁-动力吸振器系统的力学模型如图8所示，图中kdi、cdi、mdi分别为针对第i阶模态动力吸振器的刚度、阻尼系数和质量。

图8 力学模型图

由动力吸振器产生的反馈力Fdi可以表示为：

(34)

包含动力吸振器的第i阶模态传递函数表达式为：

(35)

其中，

(36)

(37)

(38)

(39)

对于控制多模态的动力吸振器的设计问题可以以各个模态为单位独立考虑。将单自由度系统的最优设计法与模态控制理论相结合，可以将单自由度系统动力吸振器的最优设计推广至i阶模态制振中，由此可得针对i阶模态的最优设计。

(40)

(41)

轨道梁前2阶模态如图9所示。

图9 前2阶模态图

可见，模态变形最大位置分别在L/4、L/2以及3L/4处。因此选择在3个模态变形最大位置各安装一个动力吸振器，动力吸振器的参数按照式(9)、式(10)设计，但L/4和3L/4处的动力吸振器针对轨道梁第2阶固有频率设置参数，L/2处的动力吸振器针对轨道梁第1阶固有频率设置参数。

此时多重TMD(MTMD)动力学方程为：

(42)

(43)

(44)

3 仿真结果分析

联立车辆-悬浮控制-轨道梁-吸振器动力学方程组，选取轨道梁五阶模态，建立垂向车-轨-吸振器耦合动力学模型，部分参数见表1。

表1 垂向车-轨-吸振器耦合动力学模型参数表

根据最优同调和最优阻尼调整TMD的参数，取TMD与桥梁的质量比为0.01、0.03、0.05、0.1和0.2进行对比分析。单个TMD跨中挠度、加速度以及抑振效果对比结果如图10、图11所示。多重TMD(MTMD)跨中挠度、加速度以及抑振效果对比结果如图12、图13所示。

图10 TMD对跨中挠度影响及抑制效果

图11 TMD对振动加速度影响及抑制效果

图12 MTMD对跨中挠度影响及抑制效果

图13 MTMD对振动加速度影响及抑制效果

由图10、图11分析可知：(1)模型中单个悬浮架前后悬浮控制点距离为1.7 m，当速度为40 km/h时，悬浮控制对轨道梁激扰力的频率为(40/3.6)/1.7=6.536(Hz)，非常接近轨道梁1阶固有频率(6.443 Hz)，因此此时轨道梁动态响应较大，并且TMD的抑振效果随着质量比的增大而增大，当质量比为0.1时，位移抑制效果最好，接近7%，当质量比为0.2时，振动加速度抑制效果最好，接近60%；(2)当速度在60～160 km/h之间时，小质量比的TMD抑振效果比大质量比的TMD的抑振效果要好，这是由于列车运行频率远离轨道梁固有频率，因此轨道梁动态响应比较平稳且响应值较小，所以大质量比的TMD产生了较大的静挠度导致了位移抑制产生负控制；(3)当速度大于180 km/h时，轨道梁动态响应随着速度增大而增大，位移抑制效果也随着质量比的增大而增大，但是较大的质量比会导致轨道梁振动加速度变大。由图12、图13可知，采用多重TMD时，当悬浮控制对轨道梁激扰频率与轨道梁1阶固有频率接近，跨中挠度和振动加速度的抑制效果均超过了单TMD，最大抑制效果均出现在质量比为0.1的多重TMD控制下。此外，同等质量比下由于多重TMD质量分散在3个单TMD上，所以产生的负控制小于单TMD。

4 结论

本文将某中低速磁浮列车简化为由车体、悬浮架组成的8自由度刚体系统，建立了基于位移-速度-加速度反馈的PID主动控制模型，基于扩展定点理论与频率传递函数设计了单动力吸振器和多重动力吸振器，并分析了2种动力吸振器方案的最佳参数。通过对不同质量比的动力吸振器开展动力学仿真对比可以得出以下结论：

(1) 动力吸振器对轨道梁振动加速度的抑制效果显著，但对轨道梁最大位移的抑制效果较小；

(2) 当激扰力频率接近轨道梁固有频率时，轨道梁因共振而达到最大动态响应，此时0.1质量比的多重动力吸振器的振动加速度抑制效果最好，接近60%，进一步增大质量比后，制振效果下降；

(3) 当激扰频率远离轨道梁1阶固有频率时，大质量比动力吸振器容易产生负控制，而过小的质量比会使得动力吸振器的抑振效果不明显；

(4) 多重动力吸振器质量分布均匀，抑振效果优于单动力吸振器，并且负控制小于单动力吸振器。