基于雷达数据的车辆换道行为识别研究

苏丽娜，李凡，潘秀，田子立，赵建东

（1.中电建冀交高速公路投资发展有限公司，石家庄 050000；2.河北省交通规划设计研究院有限公司，石家庄 050011；3.北京交通大学 交通运输学院，北京 100044）

车辆行驶过程中，换道是一种常见交通行为，在很大程度上影响着道路交通安全.相关研究表明，在所有因换道引起的交通事故中，换道决策判断失误占据其中的75%［1］.由此可见车辆换道的安全性、可靠性和高效性与交通安全问题有着紧密的关系，对车辆换道行为进行识别已经成为微观交通流领域的重要研究内容之一.

当前，针对换道行为的研究大部分是基于视频数据和GPS 数据开展的.龙学军等［2］利用视频数据，提出了一种基于视觉的高速道路车辆换道行为预测方法，消除了多个传感间的数据依赖影响.房哲哲［3］基于GPS 数据，提出一种基于深度学习的换道模型，充分挖掘历史换道数据中存在的信息，进而对换道决策与换道过程进行预测、模拟与分析.Gonzalez等［4］基于历史GPS 交通数据，提出了一种求最短路径的算法并将其应用于大规模路网中，获取了精度较好的车辆轨迹.近年来随着智能交通发展，毫米波雷达被广泛应用于交通领域，它在速度检测、换道辅助、自动驾驶以及多传感器数据融合等应用中逐步发挥重要作用.雷达检测器已在国内高速公路逐渐安装应用，其采集的数据为换道行为识别提供了数据支撑.Mekker等［5］使用激光雷达和联网的车辆数据来识别拥堵状态和排队时间，然后评估道路对齐对高速公路交通运营的影响，并识别不符合规范的路段.Serafin等［6］设计了一种基于雷达数据的检测算法，该算法能够判断出高速公路上车辆停车和驻车的行为，并提前向其他司机发出谨慎驾驶、减速慢行的警告.

在换道行为识别模型方面，国内外研究人员的研究已经有了一定的进展，相关学者从各个角度对换道行为识别进行了建模与分析.刘昀晓等［7］研究了车辆轨迹的关联算法，利用K 近邻联合概率将车辆检测点进行关联，提高了轨迹跟踪的精度.戢晓峰等［8］建立了基于支持向量机的货车移动遮断下小客车驾驶行为识别模型，对小客车地跟驰、换道和超车这3 种驾驶行为类别进行识别.Gindele等［9］构建了动态贝叶斯网络滤波模型，识别预测驾驶员的行为轨迹.Dogan等［10］基于驾驶模拟试验数据，分别构建了前馈神经网络、递归神经网络和支持向量机3 种换道识别模型，通过对比分析发现支持向量机识别效果更理想.为提升模型的识别精度，近年来研究学者逐渐对模型进行改进，袁伟等［11］利用遗传算法确定惩罚参数C和核函数g的最优组合，建立了支持向量机识别模型.Zhang等［12］建立了基于BP 神经网络寻优的支持向量机回归自动驾驶决策识别模型.陈亮等［13］设计了一种基于多分类支持向量机的车辆换道识别模型，研究证明该模型能够很好地识别车辆在换道过程中的行为状态，为车辆换道阶段的研究提供支持.

综上所述，在高速公路换道行为识别方面，基于雷达数据开展研究的成果较少，识别模型也逐渐由单一模型转变为组合模型.因此，基于实际路段的雷达数据，解决原始数据中存在的异常值、轨迹不连续等问题，结合粒子群算法以及支持向量机算法构建车辆换道行为识别模型实现高速公路车辆的轨迹跟踪及换道行为识别，使路侧雷达数据得到更好的挖掘应用，为智慧高速的交通管理提供技术支撑.

1 基于雷达数据的轨迹提取

1.1 原始数据

雷达检测器固定于高速公路龙门架上，能够检测双向六车道及应急车道的车辆运行数据，检测路段总长268.92 m，道路示例如图1 所示.

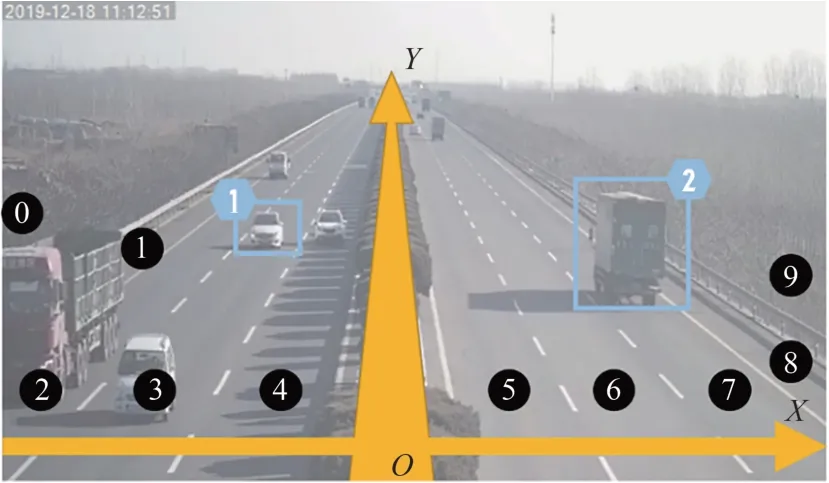
图1 车道、坐标及车型的数据示例Fig.1 Data example of lane,coordinates and vehicle types

采集的原始数据包括时间、目标车辆ID 即检测到的不同车辆的唯一编号、车辆坐标及速度等字段，X、Y方向分别代表道路的横向与纵向，其中X=0代表道路中心线，即可以通过X的正负区分车辆的行驶方向；vx代表横向速度；vy代表纵向速度；检测范围中车道号2、3、4 为左侧道路，车道号5、6、7 为右侧道路，车道号0、1、8、9 代表实线外区域；车型中1 表示小车，2 表示大车.其中采集到的2019 年12 月18 日的部分数据如表1 所示.

表1 雷达数据样例Tab.1 Example of radar data

1.2 轨迹生成与清洗重构

雷达检测的是目标物体在某一时刻的位置及运动状态，并通过检测算法识别出目标车辆的车型等信息.将不同时刻检测到的同一车辆串连在一起，这个过程即轨迹的生成，共有3 个步骤.

步骤1：从采集到的数据中的第一条开始，记录下目标车辆ID 以及X、Y坐标，轨迹序列初始化为集合A1.

步骤2：遍历下一时刻数据，若找到目标车辆ID相同的一条数据则进行下一步，否则重复步骤2.

步骤3：对时间相邻两点的位置进行判定，设定条件为

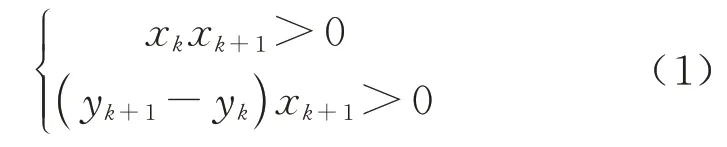
式中：xk为目标车辆在检测点k的X坐标；yk为目标车辆在检测点k的Y坐标.

若满足条件，则运动方向为正向，且不会跨越物理间隔，则认为两点为同一轨迹，轨迹序列扩充为A1，A2，…，Ak+1；若不满足条件，则该条轨迹结束，并从步骤1 重复以上过程，直到数据遍历完，即可初步生成所有车辆轨迹.

轨迹初步生成后存在连接错误、位移不符合实际、短轨迹数量多等问题，因此分别加入空间约束、动力约束、长度约束［14］对无效轨迹进行剔除，并对错误轨迹进行分解重构.

1）空间约束.

首先基于空间限制排除异常，即车辆行驶不可能跨过中央分隔带，即满足

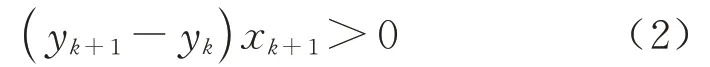
2）动力约束.

动力约束指轨迹点的匹配应满足速度、加速度等现实条件，根据时间相邻两轨迹点的坐标求得速度，根据3 点求得加速度，检验速度和加速度是否小于高速公路环境下车辆的最大动力条件，即满足

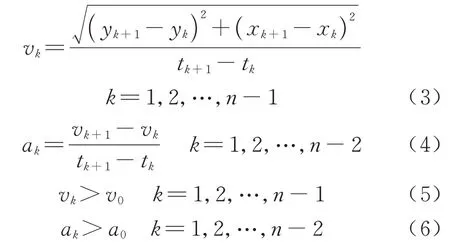
式中：vk、tk、ak分别为目标车辆在检测点k的速度、时间、加速度.

3）长度约束.

长度约束主要用于处理短轨迹.正常的一条轨迹是从进入检测范围到驶出检测范围的一段完整记录，但从检测结果来看，存在很多检测点少、长度短的异常轨迹.因此为剔除异常轨迹的影响，加入

式中：n为轨迹检测点数量；N为判定短轨迹的阈值，根据统计结果取N为50.

经过3 种约束的处理，异常轨迹得到有效剔除，最终有效轨迹共1 009 条，分别用不同颜色的线条进行表示，处理前后的轨迹对比如图2 所示.

由图2 可知，异常轨迹多分布在道路外侧，且短轨迹具有明显的空间特征，主要分布在靠近检测器的道路外侧.这是由于这部分位置与检测器几乎平行，雷达角度过大，数据精度低，且本身外侧车道的大车比例较多，检测器易将大车识别为两辆小汽车，因此会产生较多的异常轨迹.

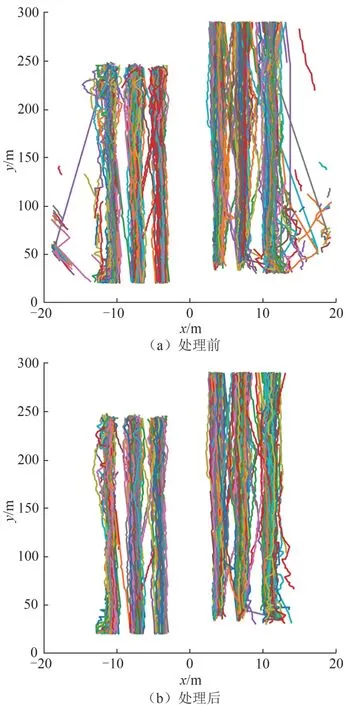
图2 处理前后轨迹对比Fig.2 Comparison of trajectories before and after treatment

1.3 轨迹平滑与匹配

基于检测点的轨迹生成算法能够对车辆目标进行稳定地跟踪，得到较好的运动轨迹，但是并不是所有的轨迹都足够平滑，在有些场景下由于天气、检测结点不稳定等原因，导致原始轨迹平滑性较差、噪声多，因此采用Savitzky-Golay 滤波器［15］对轨迹进行平滑处理，通过五点三次平滑，每4 个监测点取一点构成轨迹.平滑效果示例见图3.

由图3 可知，车辆正在换道，相比于直线行驶，换道行驶的车辆运动更加复杂，检测波动性更大，1/4 点轨迹已经消除了原始轨迹中锯齿形的特征，轨迹更加平直，有效减小了位移的波动，但仍然有轨迹不稳的趋势，呈曲率较小的波浪形；而经过五点三次平滑处理后，轨迹在换道部分形态平直，完全消除了波动，更加符合实际场景下的轨迹特征.由整段轨迹的速度方差可知，对轨迹进行平滑处理后，其横向速度方差降低了58.8%、纵向速度方差降低了31.9%；与实测速度相比，横向速度方差从4.4 倍缩小至1.81 倍，纵向速度方差从14.4 倍缩小至9.8 倍.由处理结果可知，车辆速度的异常波动减弱并趋于平稳，更接近于实际检测的速度数据.

图3 平滑效果示例Fig.3 Schematic diagram of smoothing effect

另外，在雷达监测中，常出现将一辆车识别成两辆车的情况，从而形成了异常短轨迹.为了对异常短轨迹进行匹配，首先对所有生成的轨迹做检测点个数的频数统计，轨迹检测点个数以50 为界，分为短轨迹和长轨迹，需要进行匹配的轨迹即为检测点少于50 的短轨迹.轨迹的匹配流程分为4 个步骤.

步骤1：输入异常轨迹.

步骤2：在异常轨迹的第一个检测点即t0时刻搜索同时出现的轨迹集合.

步骤3：取异常轨迹与各正常轨迹同时存在的时间点集合ts1，ts2，…，tsn.

步骤4：取该时间段内的纵坐标向量，通过某种检验方法，异常轨迹会与每条备选匹配轨迹都得到一个评价值，在认为具有相似性的条件下，取评价值最优的一条轨迹作为异常轨迹的匹配轨迹.

在步骤4 中，检验方法分别采用相关系数、符号秩检验（其评价值为p值）和弗雷歇距离，其中前两种方法的检验对象采用纵坐标y和纵向速度vy分别进行轨迹的匹配，结果如表2 所示.

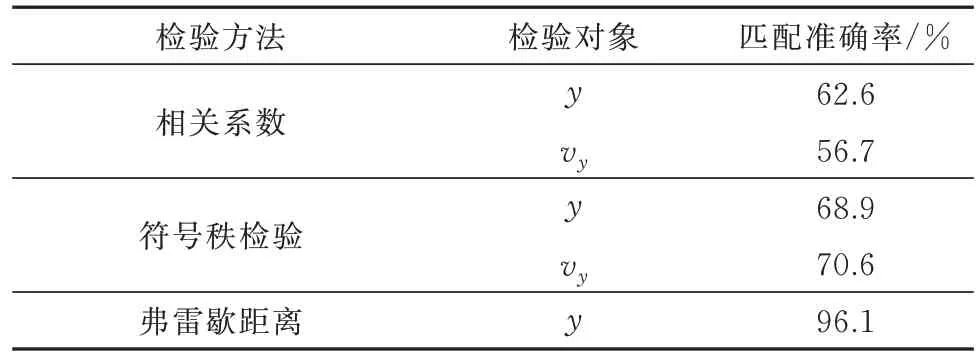
表2 各种检验方法的匹配效果Tab.2 Matching effects of various detection methods

由表2 可知，选取弗雷歇距离的轨迹匹配算法准确率最高，其次是符号秩检验，相关系数的匹配算法匹配率最低.对于检测对象的选取不同，使用相关系数评判相似性时，纵坐标的匹配效果更好；而使用符号秩检验时采用纵向速度的匹配效果更好.进一步分析两条关联轨迹，大多数情况下处于匀速状态，速度波动小，较小波动就会对相关系数结果影响很大，因此该方法并不适合用于轨迹的匹配.

弗雷歇距离是对相同时刻两点坐标的欧式距离进行研究，但雷达检测的数据中，还有一个关键的信息是速度，并且速度的精度要高于坐标的精度，因此利用速度信息来改进弗雷歇距离［16］，将改进算法应用于轨迹匹配并进行检验，轨迹匹配的准确率达到了99.4%，能够将大部分的异常短轨迹匹配到正常轨迹上.通过该轨迹匹配算法，能够找到异常轨迹出现的原因，且可以辅助修复正常轨迹中坐标、车型等信息，提高了雷达检测数据的可靠性.

2 换道轨迹特征提取

由于雷达检测长度有限，难以检测到完整的换道过程，且数据精度较低，位置波动性大，难以提取转向角度的特征，因此需要对换道轨迹进行特征分析.图4 是一段典型的换道轨迹和非换道轨迹的检测数据，包括横坐标x、横向速度vx、纵向速度vy随时间的变化.

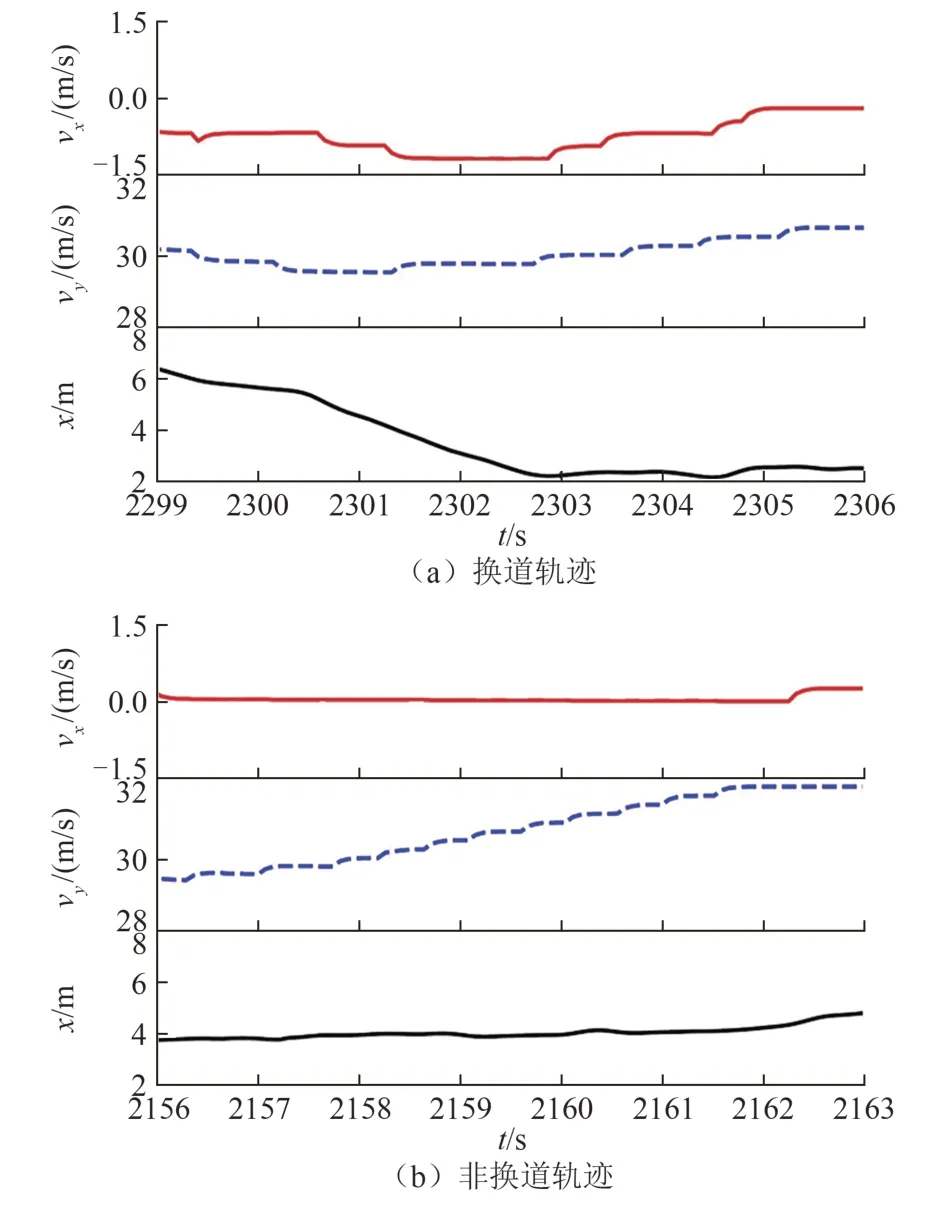
图4 轨迹特征Fig.4 Trajectory characteristics

由图4 可知，整段轨迹中换道过程中数据产生了较大的变化，主要体现在vx的增大，而其他时刻与正常轨迹无异.为研究整段轨迹中的换道过程，定义换道区间为：在一段检测的换道轨迹中，设vx的阈值为vxp，将vx＞vxp的时间区间作为该换道轨迹中的换道区间.

为提高识别效率并适应数据特点，提取换道区间的算法为：输入vx的时间序列，从时间的正向和逆向分别搜索到第一个横向速度超过换道阈值的时刻，将这两时刻分别记录为ts、te，其中s、e表示数据点的位置，[ts，te]即为换道区间.

重点挖掘偏向宏观的轨迹特征，分别从整段轨迹和换道区间中提取特征，借助换道区间，分别从角度、速度、位移和持续时间中提取出5 个特征［17］，分别为偏移角度、平均换道横向速度、平均换道纵向速度、横向偏移量、换道时长，简称为特征1～特征5.

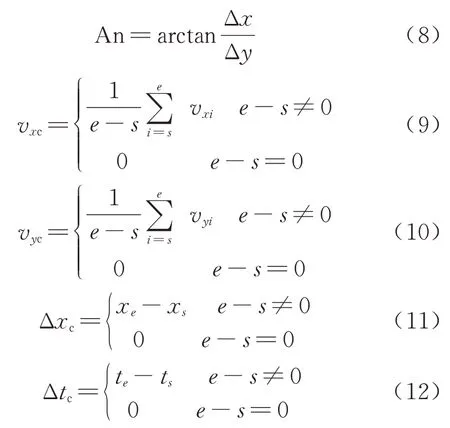
式中：An 为偏移角度；Δx为轨迹在横向的移动距离；Δy为轨迹在纵向的移动距离；vxc为平均换道横向速度；vxi为目标车辆在数据点i处的横向速度；vyc为平均换道纵向速度；vyi为目标车辆在数据点i处的纵向速度；Δxc为横向偏移量；xe为目标车辆在数据点e处的横坐标；xs为目标车辆在数据点s处的横坐标；Δtc为换道时长.

对选取的5 个特征值进行频率分析，将样本分为正类（换道轨迹）和负类（非换道轨迹），图5 分别是特征1～特征5 的频率直方图和拟合的密度曲线.

由图5 可知，特征1、2、4、5 的共性在于负类样本密度最大的点在0 附近，并随着特征值增大密度逐渐衰减，原因在于非换道轨迹中几乎不存在换道区间，而换道轨迹的这几项特征值均值更大且较为集中，概率密度接近于正态分布.其中特征1、4、5 的区分度更高，两类样本的重合度小.特征值数据如表3 所示.

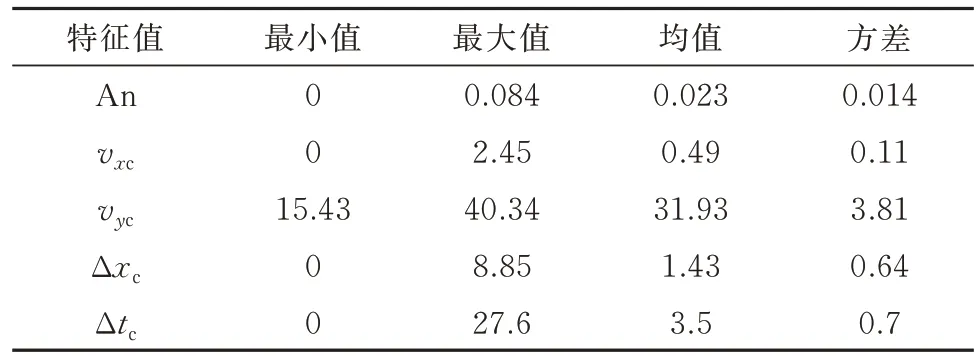
表3 特征值数据Tab.3 Characteristic value data

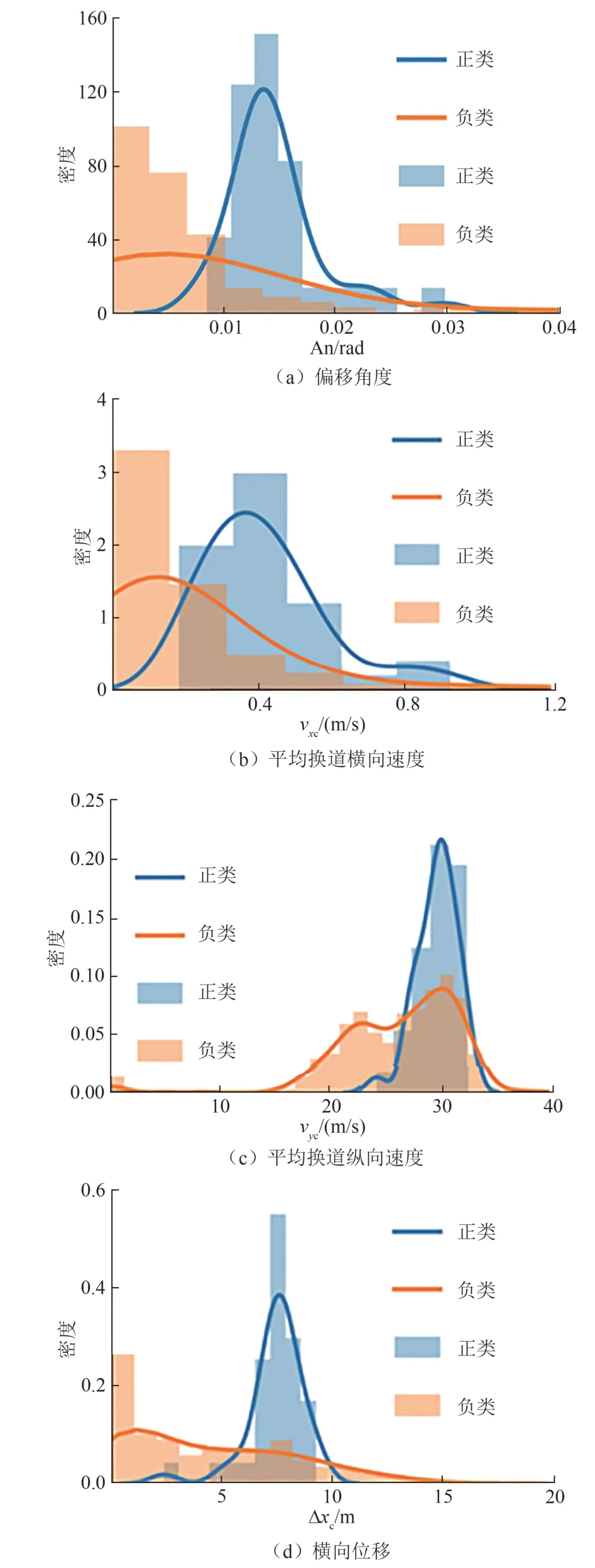
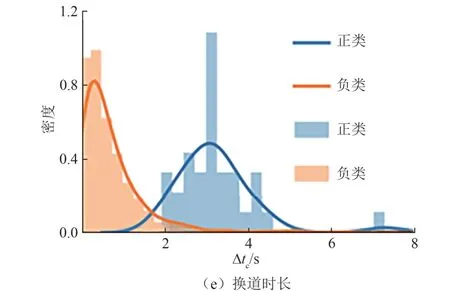
图5 特征频率直方图Fig.5 Histogram of characteristic frequency

考虑到特征方差较小但数值较大，为消除各特征值之间量纲的影响，减小各特征值的样本差异，对样本的所有特征值归一化，从而增强特征之间的可比性，以换道时长Δtc为例，对样本作归一化处理

3 基于支持向量机的换道轨迹识别

3.1 基于支持向量机的识别模型构建及优化

支持向量机是一种二分类模型［18］，适用于小样本分类模型.径向基核函数（Radial Basis Function，RBF）［19］是SVM 中应用最多的一种核函数，RBF 需要确定2 个参数γ以及C，本文先选择网格搜索法和交叉验证对参数进行选优，并分别训练30 次以消除正类样本小对结果的影响［20］.考虑到网格搜索法需要遍历网格中所有的点来寻找最优参数，其搜索时间较长.而粒子群算法［21］属于启发式算法，不必遍历区间内所有的参数组也能找到全局最优解，其优势在于不涉及多参数调节.因此，本文又利用粒子群算法构建了基于SVM-PSO 的换道行为识别模型，对参数进一步寻优.网格搜索法与PSO 算法寻优后的参数γ、C分别设置为（12，0.75）、（16，0.46）.

3.2 换道轨迹识别

在处理后的1 009 条有效轨迹中，换道轨迹34条，非换道轨迹975 条.由于换道轨迹样本占比小、样本分布不均衡，因此采用合成少数类过采样技术（Synthetic Minority Oversampling Technique，SMOTE）将换道轨迹数据从34条补齐为975条［22］.分别以6∶4、7∶3、8∶2 的比例划分训练集和测试集，即分别采用1 170 条数据、1 364 条数据、1 560 条数据（其中换道数据与非换道数据占比为1∶1）对所构建的模型进行训练，并采用剩下的780 条数据、586 条数据、390 条数据对模型进行测试，通过实例验证对比分析不同的划分比例对模型预测精度的影响，最终选取训练集和测试集的划分比例为8∶2［8］，即1 560 条训练数据，其中换道数据与非换道数据均为780 条；390 条测试数据，其中换道数据与非换道数据均为195 条.

为评价SVM模型的效果，引入E1、E2、E33 个指标

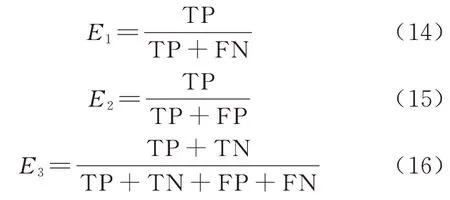
式中：E1为召回率，代表正确预测为正类的数量占实际为正类的数量的比例；E2为精确率，代表正确预测为正类的数量占预测为正类的数量的比例；E3为准确率，代表正确预测的数量占所有样本总数（包括正确的正类和负类）的比例；TP 为实际为正类且预测为正类的样本数；FN 为实际为正类但预测为负类的样本数；FP 为实际为负类但预测为正类的样本数；TN 为实际为负类且预测为负类的样本数.

3.3 实例分析

为验证所提方法的有效性，选取DBN 模型和LSTM 模型进行对比，其中，DBN 模型的网络结构设置为5-5-5-2（输入层神经元数量为5，2 个隐藏层神经元数量均为5，输出层神经元数量为2），学习率为0.001，迭代次数为100；LSTM 模型的结构设置为5-7-4-2（输入层包含5 个神经元，第1 隐藏层包含7 个神经元，第2 隐藏层包含3 个神经元，输出层包含2 个神经元），学习率为0.001，时间步time_step 为20，批量大小batch_size 为40.各模型识别的结果评价见表4.

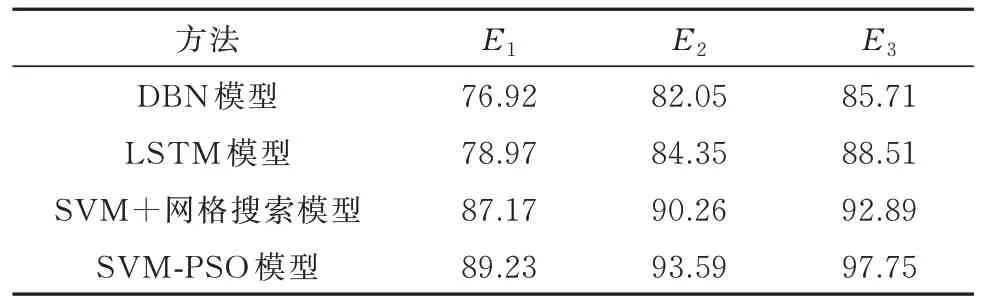
表4 训练结果对比Tab.4 Comparison of training results %

由表4 可知，5 个特征都能够用于区分换道轨迹和非换道轨迹，SVM+网格搜索模型和SVM-PSO模型识别效果较好，DBN 模型和LSTM 模型识别精度较差，说明了SVM 在处理小样本量数据时学习能力强、模型泛化性能好，不易陷入局部最优.SVM-PSO 模型的准确率和精确率都较高，分别达到了93.59%和97.75%，但召回率较低，原因在于非换道轨迹易于识别，换道轨迹难以识别.实验结果也进一步证明了在车辆换道时，有较大的概率会提速或保持高速换道的状态，推测这种驾驶行为的产生是为了通过换道超越前车，也可能是为了缩短换道时间以减少换道行为对交通流及车辆安全性的影响.

4 结论

1）根据车辆运行状态初步生成轨迹，并通过多重条件约束对轨迹清洗重构，采用Savitzky-Golay滤波器对轨迹平滑处理，通过五点三次平滑，横向速度的方差从4.4 倍缩小至1.81 倍，纵向速度方差从14.4 倍缩小至9.8 倍，车辆速度相较优化前更为平稳，实现了对多车轨迹的跟踪.

2）针对异常短轨迹，研究了轨迹相似性度量的方法，并提出了一种基于弗雷歇距离的改进轨迹匹配算法，将异常短轨迹与正常轨迹匹配，匹配率达到了99.4%，使轨迹数据得到进一步修复.

3）提取轨迹的偏移角度、换道时长、平均换道纵向速度、平均换道横向速度和横向位移5个特征，分别利用DBN模型、LSTM模型、SVM模型以及SVM-PSO 模型对换道轨迹进行识别，发现SVMPSO 模型识别效果最好，准确率达到93.59%，精确率达到97.75%.