基于空间联系强度的城际出行分布预测模型

彭辉，王威，徐培娟，潘卫龙，刘丹

（长安大学a.运输工程学院，b.公路学院，西安 710064）

随着我国城市群的快速发展，加强城际交通系统基础设施建设来满足日益增长的城际出行需求是建设“交通强国”的重要举措.相比市内出行，城际交通出行在出行目的、出行时间、费用以及出行分布等方面均有不同.目前主要基于四阶段方法［1］、大数据［2］等方法研究城际交通需求分析，而在工程实践中多直接套用城市交通需求预测的方法，忽略了城市群城际出行的特性，缺乏对城际交通分布量的精确预测，使得规划设计与实际客流量偏差较大.因此，为获得更为可靠的城际出行分布量，城际的出行特征规律和更精确的出行分布模型有待考虑.

一直以来，出行分布模型都是国内外学者的研究热点和重点.国内外常用的出行分布模型主要有增长系数模型［3］和综合模型［3-4］两类，随着居民出行规模的不断增长与出行特征的不断变化，出行分布预测难度越来越大，传统模型存在的问题愈发明显，如预测误差偏大、适应性受限等问题，因此出行分布模型的改进逐渐成为研究热点.Fiseher等［5］将神经网络引入到出行分布预测中，建立了相应的预测模型，解决了诸多复杂的出行分布预测问题.林友芳等［6］改进神经网络，提出基于时空长短期记忆网络的分布预测模型，捕获出行分布在时间和空间维度上的相关性.Mikkonen等［7］分析了在实际规划应用中重力模型参数变化的原因，并提出了相应的改进措施.Kushner［8］将介入机会模型进行了改进，并应用到出行分布预测当中.Cascett等［9］在出行分布预测研究中加入自主定义的主导变量，认为当某个目的地的主导变量大于其他所有目的时，出行者会选择该目的地.姚荣涵等［10］结合最大信息熵原理，构建了基于原点矩典型特征量约束的出行分布模型，为出行分布预测提供了一种新思路.李旭宏［11］针对固定联系、出行习惯等特殊因素，在出行分布模型中引入了特征变量，以此为基础构建了供求平衡预测模型.邓明君等［12］引入出行成本、小区土地利用等变量改进现有模型的参数，有效地降低了增长系数模型和重力模型的预测误差.朱鸿国等［1］考虑到城市群内各城市的区位影响因子对出行分布的影响，提出了基于区位理论的改进重力模型，通过建立城际间的出行分布概率矩阵来预测出行分布量.

综上所述，现存的国内外出行分布模型的研究多是针对城市出行，对于城际出行分布模型的研究较少.城际出行与城市出行在影响因素、出行特征等方面有着较大差异，在城市群体系中，空间联系与交通出行密不可分，城市群中各城市之间由于资源配置、产业分布等原因有着巨大差异，由此产生了特有的相互之间的空间联系，而空间联系的强弱直接影响了城际客流的分布规律.为此，本文从城际出行活动模式出发，在量化城市群各模式空间联系强度的基础上，构建基于空间联系强度的城际出行分布模型，计算城际间不同活动模式出行分布量，累加各模式出行分布量从而得到城际出行分布矩阵.本文将空间联系强度与城际出行分布模型结合，为城市群城际交通需求预测理论研究提供新的思路.

1 不同出行模式的空间联系强度计算

1.1 改进的经典引力模型

引力模型是计算空间联系强度最常用的模型之一，基本原理为：假设空间联系强度与两城市间的城市质量乘积成正比，与距离的平方成反比，即

式中：Fij表示城市i和j之间的空间联系强度；mi、mj分别表示城市i和j质量，一般由城市的人口、GDP决定；rij是城市间的距离；K是介质常数.

经典引力模型表现形式简洁、适用性广，但随着城市群的发展，城市质量受多因素影响，除城市的人口与GDP 以外，产业分布、社会固定投资、人均可支配收入等均影响着城市质量.所以，本文引入结构方程模型，选取能够表征城市质量的多项指标对其进行综合评价，进而提高空间联系强度的计算精度.

结构方程模型最早由瑞典学者Joreskog 于1970 年提出，它的主要作用是借助测量模型和结构模型有效处理多个潜变量，通过变量的协方差矩阵得到自变量对因变量的作用效果，是一种分析多类型变量之间关系的统计方法［13］.本文选取城市吸引力、城市辐射力、城市流动力3 个变量作为外生潜变量，城市质量作为内生潜变量，即影响城市质量的因素为城市的吸引力、辐射力、流动力.其中，城市的吸引力是指城市因为基础设施、社会服务、就业机会等优势产生了集聚效应进而吸引其他城市与自身进行交流；城市的辐射力是指城市由于自身行政地位或经济区位优势所具有的技术、资本、文化、信息和劳动力等要素对于周边区域产生的带动作用；城市的流动力是指其人员、货物与其他城市往来联系的密切程度，在一定程度上可以理解为城市的对外流通能力［14］.

由于数据以具有代表性、完备性同时又易于获取为原则，本文建立了观测变量指标评价体系，各潜变量与其对应的观测变量如表1 所示.

表1 潜变量及观测变量Tab.1 Latent variables and observed variables

表1 中数据可由各省市统计年鉴获取.在对结构方程模型的路径进行设定后，运用Amos Graphics软件对模型进行计算，检验模型的拟合度与因子荷载的显著性，得到路径系数与观测变量对潜变量的因子荷载.

本文通过对引力模型的分析，结合结构方程模型中观测变量的得分，建立了城市质量计算模型，具体为

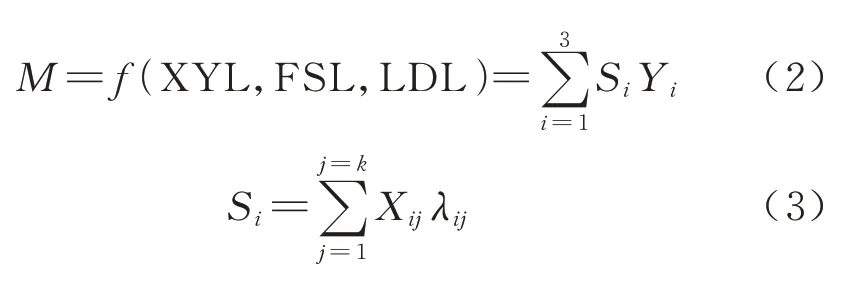
式中：M表示城市质量；XYL、FSL、LDL 分别表示城市吸引力、辐射力、流动力；Si表示第i种潜变量的赋值；Yi表示第i种潜变量对城市质量的路径系数；Xij表示第i种潜变量中第j种观测变量的得分（经过标准化处理过的数据）；λij表示协方差矩阵中的因子荷载.

综上所述，通过结构方程模型对三参数的定量计算，将城市质量进行了合理有效的确定.结合式（1）～式（3）便可得到修正后的基础空间联系强度.

1.2 考虑不同出行模式的空间联系强度计算模型

城市群内居民的城际出行活动模式复杂多样，基于大量数据的调查结果［15］，本文主要从城际出行目的角度将乘客活动模式分为商务出行、旅游出行、其他出行（如购物、就医等）3 类.不同活动模式的出行分布量在一定程度上取决于城际空间联系强度的大小，但仅用一个空间联系强度很难清晰地描述城市间不同活动模式的出行分布规律，所以本文依据出行活动模式将城市空间划分为商务空间、旅游空间、其他空间，相应地将城市群空间联系划分为商务联系、旅游联系、其他联系3 类，建立“基础联系+活动模式联系”的多模式空间联系模型，如图1 所示.

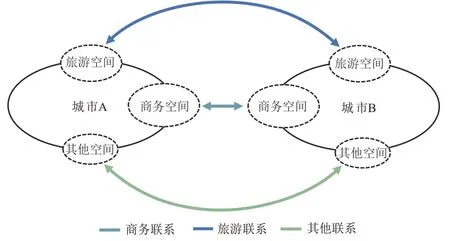
图1 城市群多模式空间联系Fig.1 Multi-mode spatial connection of urban agglomerations

1.2.1 商务出行联系

商务出行是指由社会经济活动产生的因公出行，主要包括上班、出差、经商、打工等，是城际间出行占比最高的活动模式.结合相关研究［15］可知，商务出行主要和城市间的产业关联度以及母子公司关联因素有关，因此将这两种因素量化加入到基础空间联系强度模型中.

1）产业关联度.

产业关联度泛指各个产业之间在经济和技术上所占的数额和比例，主要涉及各个产业之间的供给和需求、投资和产出之间的数额关系［16］.城市群内各产业部门之间存在着相互制约的关系，这使得分工不同的区域之间产生联系，进而促进了城际间的商务出行.本文结合投入产出分析法和灰色模型法，提出了一种计算简便、资料获取相对容易的企业关联度计算方法，具体公式为

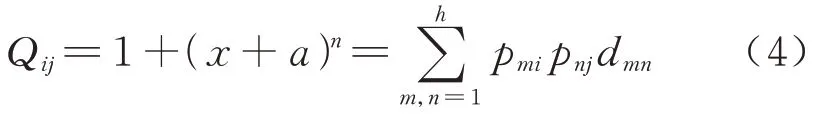
式中：Qij表示城市i，j间的产业关联度；pmi表示第m种产业在城市i中的重要度；pnj表示第n种产业在城市i中的重要度；dmn表示m产业与n产业之间的关联度（采用两产业间的投入产出完全消耗系数的平均值表示，具体数据由国家统计局官网获取）；h表示城市内产业门类的数量.

其中，各产业门类重要度计算式为

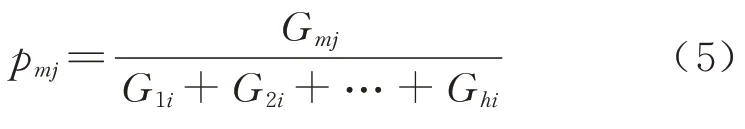
式中：Gmi表示第m种产业门类在城市i中的生产总值.

2）母子公司关联系数.

目前，伴随着经济的快速发展与交通网络的不断完善，许多大型企业为了扩大市场规模或抢占区域资源，会在多个城市设立子公司［17］.母子公司的紧密联系将产生大量的城际间商务出行，因此母子公司关联因素应成为模型构建时考虑的一部分.母子公司关联因素对城际出行起促进作用，所以母子公司关联系数应不小于1，同时考虑到不同城市间子公司关联岗位数差异较大，应采用相对值表示；基于以上两点因素构建母子公司关联系数为

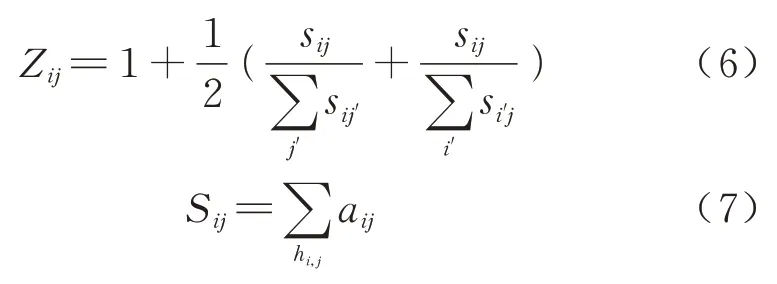
式中：Zij表示城市i与城市j间的母子公司关联系数分别表示城市i、j所涉及的所有子公司关联岗位数的总和；sij表示城市i与城市j之间的子公司关联岗位数；aij表示母公司位于城市i且子公司位于城市j的企业的子公司岗位数或母公司位于城市j且子公司位于城市i的企业的子公司岗位数；hi，j表示城市i和城市j中符合条件的企业数.

基于对产业关联和母子公司关联两个因素的量化分析，构建的城际间商务联系强度模型为

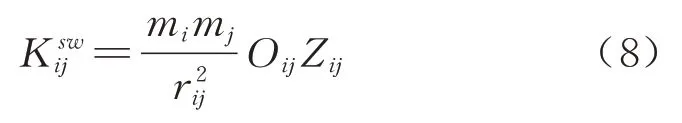
1.2.2 旅游出行联系

近年来，随着城际交通网络的建设，城市群内的旅游出行占比逐渐提升，已成为城际出行中不可忽视的重要组成部分［18］.本文在文献［19］提出的旅游空间强度模型基础上，采用相对值表示旅游联系系数，并进一步调整改进，具体为

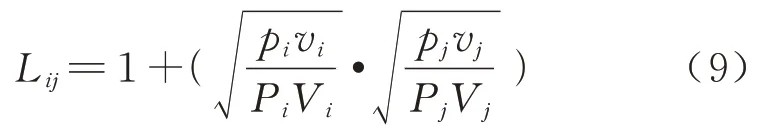
式中：Lij表示两城市间的旅游联系系数；Pi、Pj表示城市i、j的总出行量；Vi、Vj表示城市i、j的总收入；pi、pj表示城市i、j的国内旅游人数；vi、vj表示城市i、j的国内旅游收入.

将计算出的旅游联系系数代入基础空间联系强度模型中，即可得到城市间的旅游联系强度为

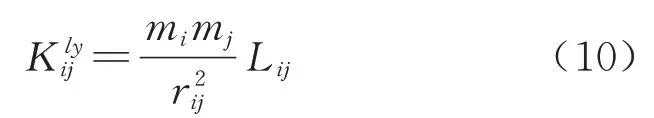
1.2.3 其他类出行联系

城际间的出行活动模式除了商务、旅游两类外还有探亲、就医、购物等模式，本文将这些活动模式产生的联系统一定义为其他联系.探亲访友联系是人的主观情感联系，主要与当地的常住人口数以及两地的距离有关，这两个因素在基础空间联系强度模型中已有体现；就医联系主要与当地的医院数量有关，因此选取城市内三甲医院的数量作为表征就医联系的指标；购物联系主要与当地的商场数量有关，因此选取城市内大型商场的数量作为表征购物联系的指标［20］.同商务联系、旅游联系模型处理方式相同，考虑到不同城市间医院、商场数量上差异较大，本文采取相对值进行表示，具体公式为

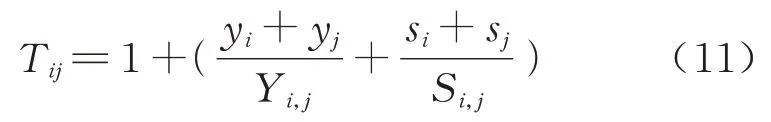
式中：Tij表示其他联系系数；yi、yj表示城市i、j的三甲医院数量；Yi，j表示城市群内所有三甲医院数量；si、sj表示城市i、j的大型商场数量；Si，j表示城市群内所有大型商场数量.

将式（11）代入基础空间联系强度模型中，得到城际间其他联系强度模型为

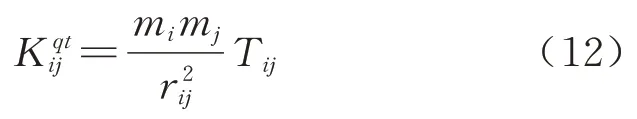
2 改进的城际出行分布预测模型

2.1 引入空间联系强度的重力模型

重力模型最初由Casey 提出，最初用于分析不同城镇间的购物行为，后逐渐成为出行分布预测最常用的方法之一［21］，它的基本原理是假定两个交通小区间的出行分布量与两个小区的出行发生量和吸引量成正比，与小区间的出行阻抗成反比.本文选用双约束重力模型作为基础预测模型，其计算公式为［22］

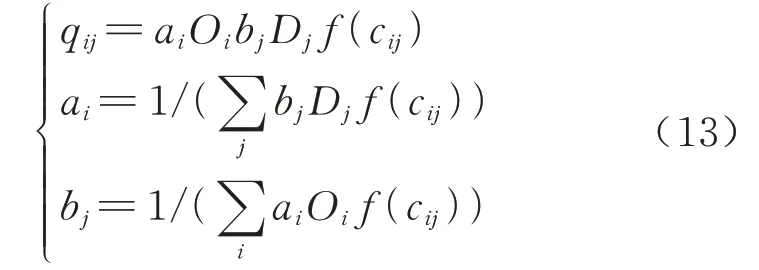
式中：Oi、Dj分别表示i小区的发生量和j小区的吸引量；f(cij)表示i小区与j小区间的交通阻抗函数；ai、bj为约束系数.

选择幂函数作为交通阻抗函数，并选择出行时间作为交通阻抗的表征指标，主要考虑不同活动模式对出行时间的宽容度不一样，故针对不同活动模式进行交通调查，确定两小区不同模式的众数出行时间.具体为

式中，tij表示两小区间出行时间；r表示待定参数.

由于计算出的空间联系强度是一个系数矩阵，因此将空间联系强度以参数的形式代入重力模型，对各类活动模式的出行分布量进行修正，形成了基于多模式空间联系强度的重力模型，即

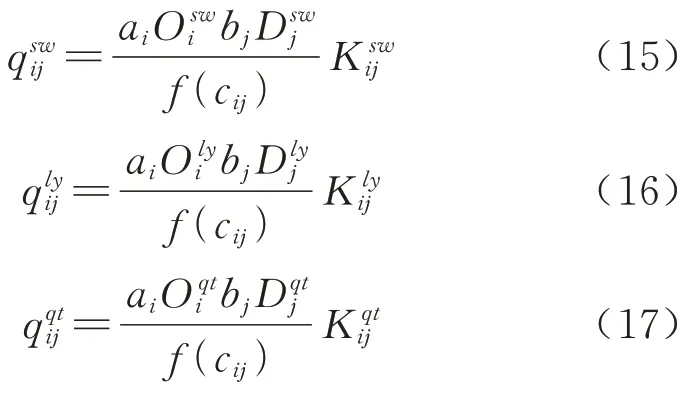
2.2 出行分布量预测

按照活动模式的不同将城市群城际出行分为商务出行、旅游出行、其他出行3 大类，各活动模式的出行分布量预测流程如图2 所示.

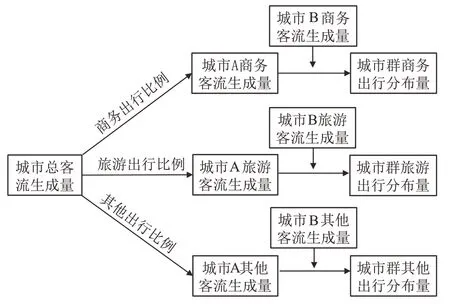
图2 不同活动模式的出行分布量预测流程Fig.2 Predicting process for travel distribution of different activity modes

依据城市出行结构确定城际出行中不同活动模式的比例；采用弹性系数法预测客流发生量和吸引量，通过分析研究区域历年交通指标与经济指标之间的相互关系，预测未来年各研究区域的弹性系数，在求得各交通小区未来年经济增长率的基础上计算其客运增长率，从而预测各小区的出行发生、吸引客运量.

根据各种模式出行比例计算出各模式的出行生成量后，将相关数据代入式（15）～式（17），得到商务出行、旅游出行、其他出行的分布矩阵，将3 类活动模式的出行分布矩阵求和便可得到城际出行分布总量矩阵qij.

3 实例分析

选取关中平原城市群为研究对象，主要针对研究范围内的5 市（西安市、咸阳市、渭南市、铜川市、宝鸡市）一组团的出行分布量预测进行分析计算.本次预测的基础年度选为2014 年，预测年度选为2019 年.

3.1 利用结构方程模型计算城市质量

原始数据来源于2019 年陕西省各地级市的统计年鉴以及从相关部门获取的资料，对原始数据进行标准化处理，借助SPSS 软件中的Reliability Analysis 功能对样本数据的一致性进行信度分析，得到外生潜变量和内生潜变量的信度都在0.8 以上，说明潜变量所对应的观察变量的样本数据值一致性较高.将处理好的数据代入结构方程模型，其中δi、ei εi为各变量间的测量误差项，利用AMOS 软件进行路径求解，将输出结果进行标准化处理，结果如图3 所示.

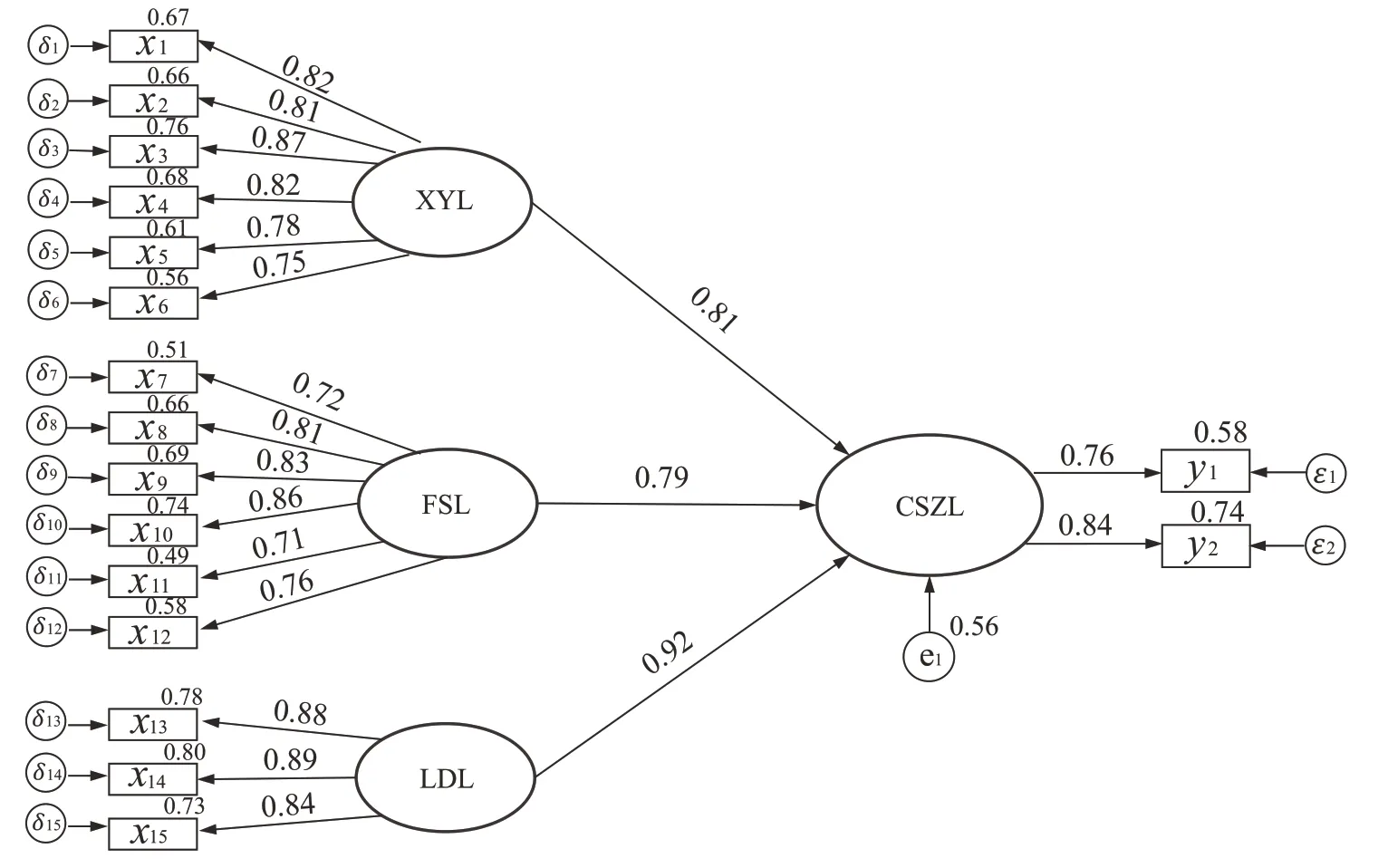
图3 结构方程模型计算结果Fig.3 Calculation results of structural equation model

由图3 可知，吸引力、辐射力、流动力对城市质量的路径系数分别为0.81、0.79、0.92，其中流动力对城市质量影响最大.各潜变量与观测变量之间的因子荷载均大于0.6，说明观察变量能够较好地解释潜变量.

将因子荷载、路径系数、观测变量得分归一化后代入式（2），计算西安、咸阳、渭南、铜川和宝鸡5个城市的质量分别为：0.967、0.305、0.286、0.096、0.274.

3.2 计算多模式空间联系强度

结合式（12），代入相关数据，并将结果归一化处理，关中平原城市群五市间商务联系强度、旅游联系强度、其他联系强度计算结果如表2～表4所示.

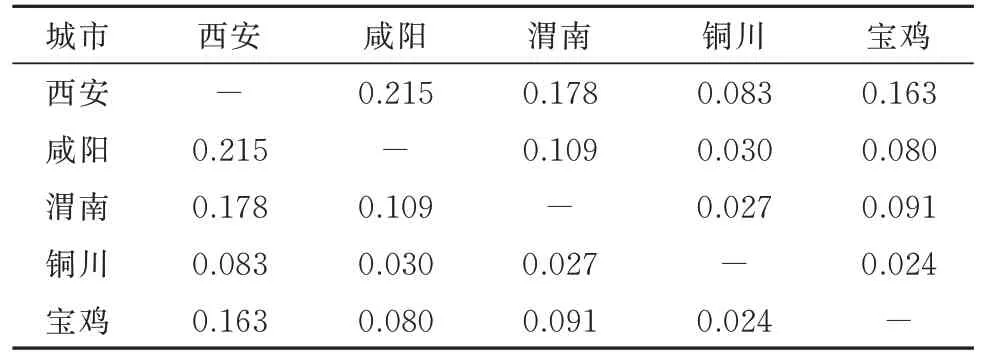
表2 商务联系强度Tab.2 Strength of business connections

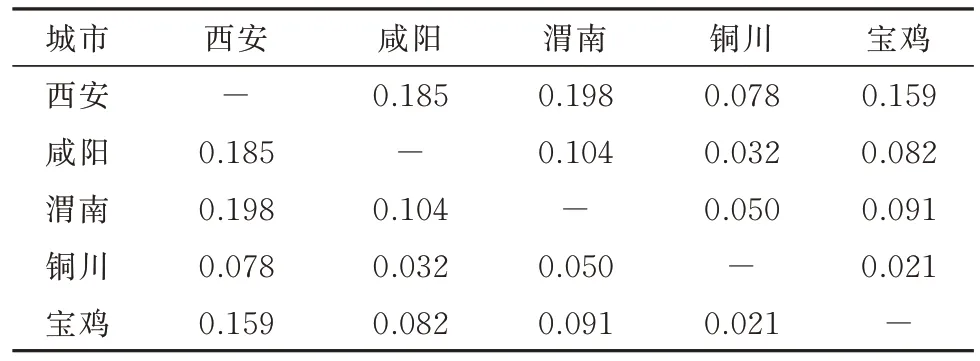
表3 旅游联系强度Tab.3 Strength of tourism connections

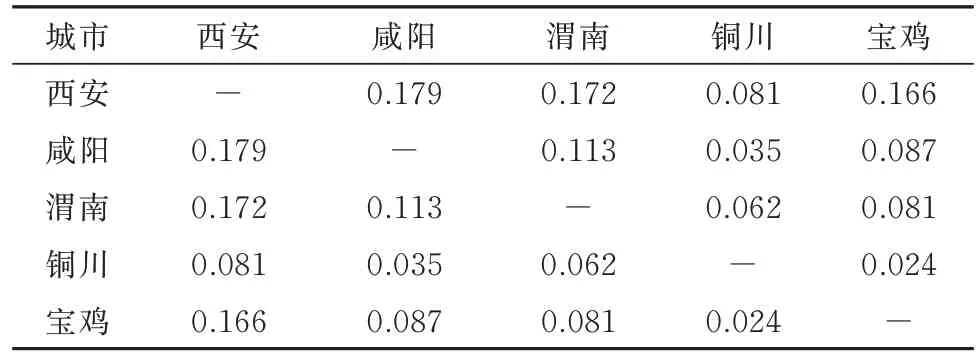
表4 其他联系强度Tab.4 Strength of other connections

经过计算可知，商务、旅游、其他三类联系中西安的联系总量都为最大，铜川的联系总量都为最小，这主要和两市的人口和经济发展水平有关；在商务联系中咸阳的联系总量位居第二，主要原因是咸阳与西安之间存在频繁的商务交流；在旅游联系中，渭南的联系总量位居第二，主要原因是渭南市存在着丰富的旅游资源且距离西安较近，旅游出行较为便捷；在其他联系中，渭南与咸阳的联系总量几乎持平，宝鸡由于地理位置的原因，大型商场和三甲医院数量较少，联系总量位于第四位.各城市之间三类空间联系强度如图4 所示.

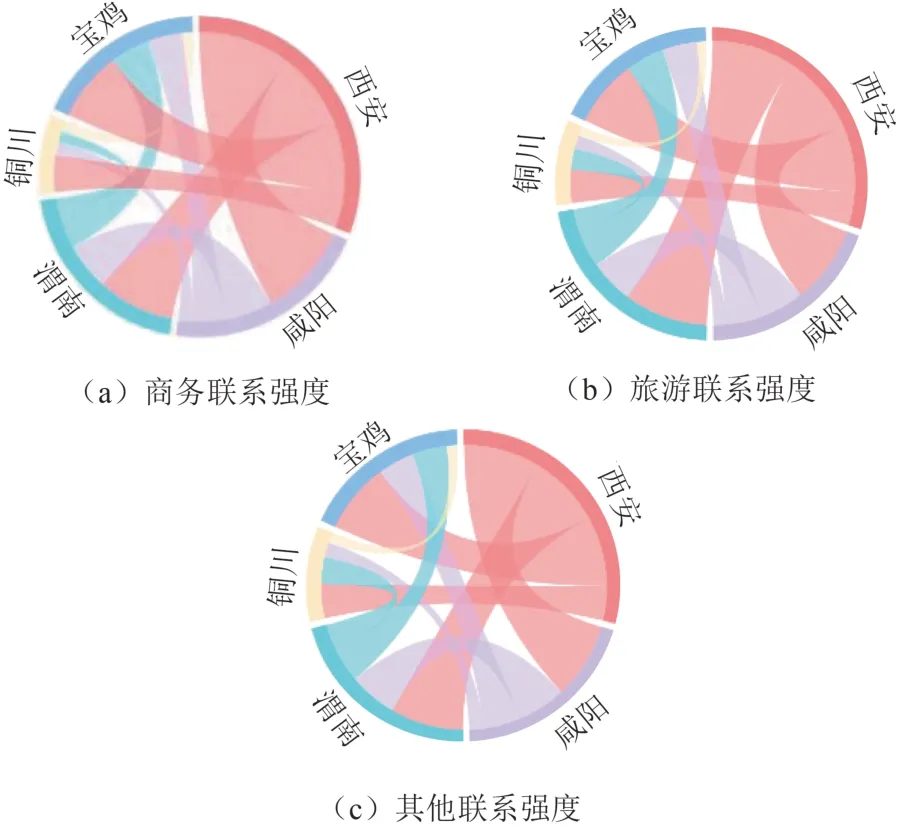
图4 空间联系强度Fig.4 Spatial connection strength

3.3 出行分布量预测

关中平原城市群5 个城市有着鲜明的自身特征及城市发展特色，使得各城市的出行结构保持着稳定的发展，在参考关中平原城市群城际铁路交通调查及客流预测报告［23］调研资料的基础上，考虑到城市群以单核城市群为主，城市间的功能定位清晰、稳定，且2014 年和2019 年各模式出行比例变化幅度不大，故认为本研究的基年及预测年内各出行模式的比例将保持较小的变化，变化量可忽略不计，最后确定关中城市群商务出行、旅游出行和其他出行三种活动模式的城际出行总量比例分别为：45.53%、21.49%和32.98%.利用弹性系数法对各模式出行生成量进行预测，结果如表5 所示.

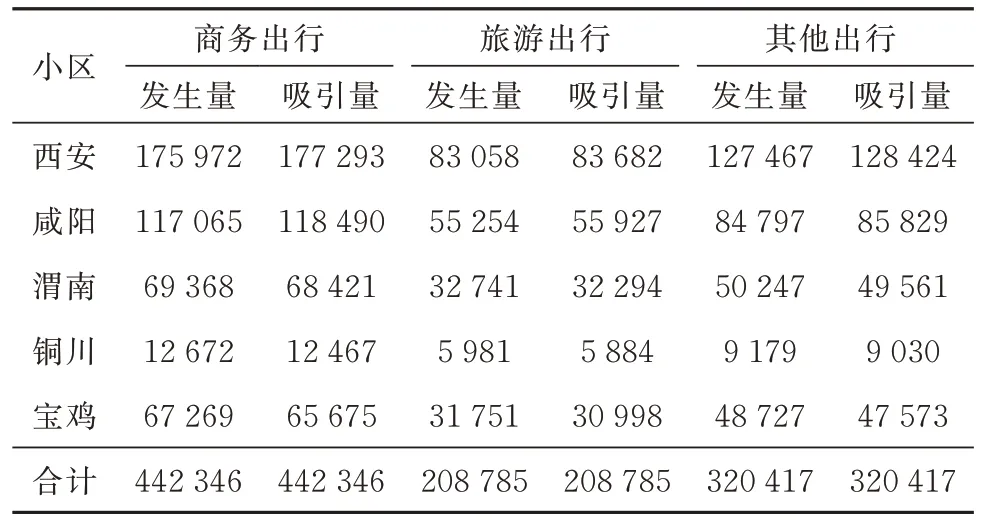
表5 预测年各城市不同活动模式发生吸引量Tab.5 Occurrence and attraction of different activity modes for different cities in the forecast year 人次/天

依据本文提出的出行分布预测模型，结合现状OD 矩阵和各小区间交通阻抗，借助Matlab 软件标定相应参数值［24］.根据式（15）～式（17），代入相关数据，借助TransCAD 软件分别计算各类活动模式出行分布量，计算结果如表6 所示.

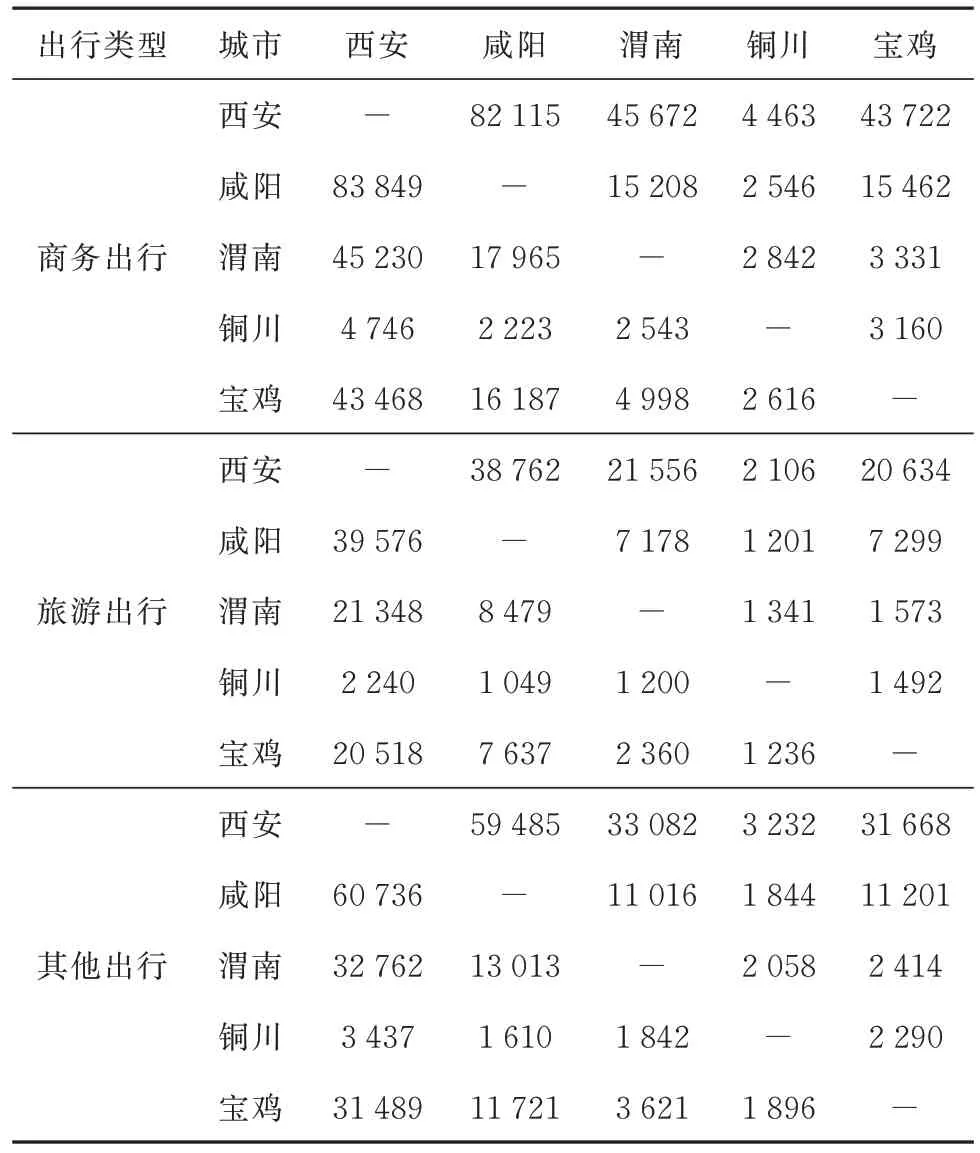
表6 预测年各城市商务、旅游、其他出行分布表Tab.6 Distribution table of business,tourism and other travel at different cities in the forecast year 人次/天

累加三类活动模式的出行分布矩阵得到出行分布总量，为了更清晰直观地描述五市之间的出行分布量的关系，绘制出行期望线如图5 所示.

图5 各活动模式出行分布量Fig.5 Travel distribution of various activity modes

根据2019 年陕西省各市的腾讯迁徙数据与联通公司提供的手机移动信令数据，将两种数据整合得到2019 年关中平原城市群五市间的实测出行分布量.为了验证本文构建模型的有效性，将模型预测的出行分布总量结果与实测数据进行校核，同时与传统模型（未进行修正的双约束重力模型）预测结果进行对比，如图6 所示.经过计算可知，本文构建的城际出行分布预测模型平均误差率为11.49%，说明计算得到的出行分布量与实际分布量基本一致；传统模型平均误差率为15.78%，与传统模型相比，本文构建的城市群城际出行分布模型预测精度有了明显提升.

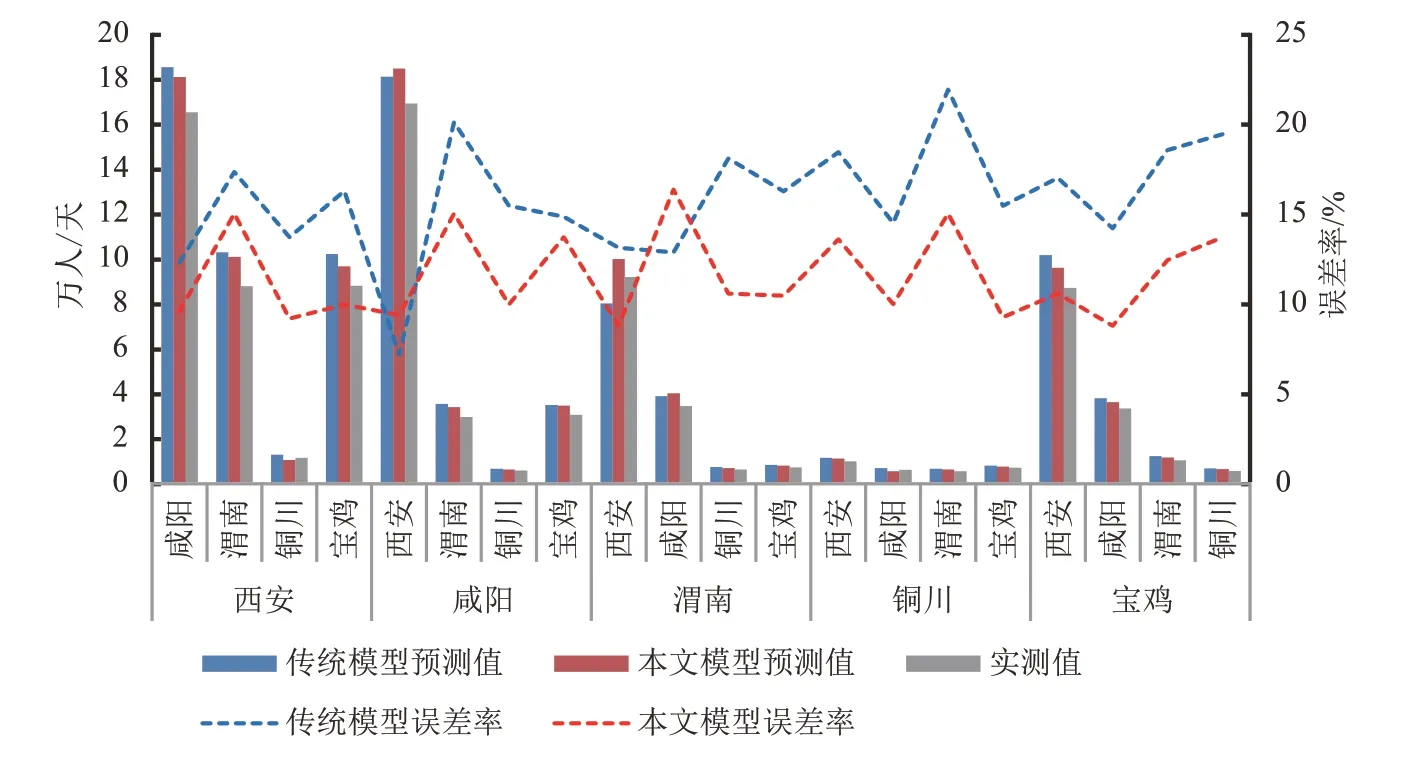
图6 城际出行分布量预测结果校核Fig.6 Verification of prediction results for intercity travel distribution

4 结论

1）在传统引力模型的基础上，利用结构方程模型构建城市质量计算方法，将城市群空间联系细化为商务联系、旅游联系与其他联系3 类，搭建了产业关联度、母子公司关联系数、旅游联系系数等参数计算方法，进而建立了空间联系强度的计算模型.

2）在城市群城际出行分布预测阶段，利用空间联系强度作为参数对传统重力模型进行修正，然后分别计算不同活动模式的城际出行分布量，对提升城市群城际出行分布预测的精确性进行了探索.

3）以关中平原城市群为例，计算分析了五市间商务、旅游与其他联系强度，以及各市之间各种出行模式下的交通出行分布，结果表明本文模型预测的平均误差率为11.49%，比传统模型减少了4.29%，通过相关方法验证了模型的有效性，推动模型在工程实践中的应用.

4）本文考虑的空间联系类型较为典型和直观，随着城市群的空间、产业、交通的不断演化，空间联系的类型将不断丰富，后续研究可对空间联系的划分及相应的模型构建做进一步细化探究，对比不同模型的预测精度，使预测结果与实际出行更加吻合.