基于力反馈的造波机主动吸收技术扭矩计算方法研究

倪艺萍 王磊 李玉刚 林俊 陈俊 王天奕

(1.珠江水利委员会珠江水利科学研究院 广东广州 510611;2.大连理工大学深海工程研究中心 辽宁大连 116024)

通过海洋工程试验水池对海洋中的风、浪、流等海洋环境进行模拟试验研究，尤其是通过造波机来实现波浪的产生。但是，在实际模型试验过程中，由于水槽或水池等设施与真实的海洋环境相比有固定边界限制，所以，在水槽或水池中往往会有二次反射波的产生。造波机产生的入射波遇到造波机对面的池壁时会产生反射波，反射波传播至造波板处会生成二次反射波，二次反射波会叠加到原始入射波之中，扰乱波浪场，破坏试验的准确性，降低试验可靠度[1]。

理论研究表明，在摇板式造波系统中应用主动吸收技术可以很好地减少甚至消除二次反射波，减少必要造波时间，延长物理模型试验时间，减少波浪平稳时间，提高物理模型试验效率；其次，采用主动吸收系统可以减少波浪模拟设备占地面积，减少投入成本，造波设备布置更加灵活。主动吸收系统根据所用传感器的不同分为力反馈式主动吸收系统和位移反馈式主动吸收系统。力反馈式主动吸收系统采用固定在波板上的力传感器进行波浪力的数据采集，位移反馈式主动消波系统采用浪高仪进行波浪高程的数据采集[2]。该文主要研究力反馈式主动吸收系统，主动吸收系统采用力传感器进行数据采集有以下几点优势。

首先，力传感器测量的是流体在波板处的压力的平均值，是压强积分的结果，要想在存在二次反射波的情况下获得有效的数据，只需要在造波板上平均布置多个测点，而且力反馈式主动吸收吸收系统多适用于干背式造波机，流体力的值仅与造波板前的水域有关。

其次，对于摇板式造波机，由于摇板围绕支撑点摇摆造波，在板上不适合布置浪高仪，而摇板运动对力传感器的干扰较少，所以布置力传感器可以更加方便数据的采集。

最后，力传感器便于将来自力传感器的信号和来自速度传感器的信号结合起来，使得造波机和流体成为一个耦合的动力系统，提供了对系统输入/输出功率的直接测量，从而修正造波机的输出信号。且在摇板式造波机规则波试验中，采用力反馈式主动吸收系统可减少水池中高阶伪谐波的产生[3]。

但是，目前国内主动吸收研究多集中在位移反馈式主动吸收，对力反馈式主动吸收的研究尚浅，且遭到国外技术封锁，虽然英国爱丁堡Flowave水池已实现该技术，但国内还未形成一个完善的理论系统，主要因为它有以下3个关键技术难题。

（1）现有的力反馈理论研究多基于理想的线性波理论，忽略非线性高阶项的影响，近似误差较大。

（2）多向不规则波浪的来波识别：现有理论限制性条件较多，多采用经验校准吸收的方法。

（3）造波机的吸收控制：滤波器设计实现较为困难。

研究水池中典型的造波方法，针对该文的主动吸收系统以力反馈的特点，基于势流理论对干背式摇板造波条件下造波板速度势解和压强的分布特性进行研究，给出单向、多向、规则、不规则造波条件下造波板上波浪作用扭矩的计算分析方法。

1 二维造波理论

建立坐标系使得z轴向上为正并与造波板的平均位置相重合。造波机沿y轴布置，x轴与静水面相重合，z=0，静水深度为h，池底位于z=-h处。

假定造波板做小振幅简谐运动，产生的波浪沿着x轴正方向传播，设造波板的铰链中心与池底间的距离为l，造波板转动中心位于z=-（h+l）处，当铰链中心位于池底之上时，l＜0，定义参数d=-l；当铰链中心位于池底或池底下方时，l≥0，d→ 0；当为推板式造波机时，l=∞且d=0。示意图具体见图1。

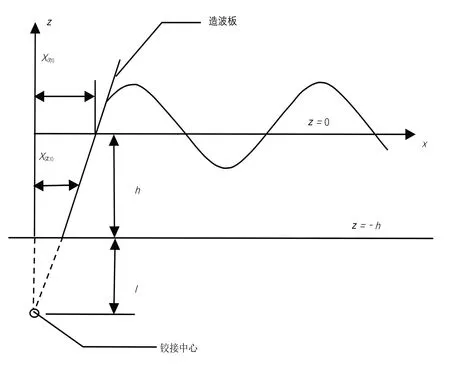
图1 力反馈式主动吸收试验布置示意图

假设水池内为无粘性且不可压缩的无旋流体，在笛卡尔坐标系（x,z）中速度势表示为Φ(x,z,t)，则速度表示为(u,w)T=(∂Φ/∂x,∂Φ/∂z)T，波面函数为η=η(x,t)，波板位置X=X(z,t)；静水水面z=0处波板位置为X0(t)。θ、ω、g、t分别表示造波板角位移、波浪频率、重力加速度和时间[4-5]。

1.1 控制方程

假设流体质量守恒且不可压缩，因此，在流场中流体满足拉普拉斯方程

1.2 自由水面条件

假设水面高度为z=η(x,t)，则自由水面处水质点运动规律的函数可表示为

水面截面处的流线符合运动学自由水面边界条件，根据该边界条件得

另外，水面压力符合动力学自由水面边界条件，其中，自由水面处的压力等于其上方的大气压力，所以压强为零，由伯努利方程得

假定波浪波幅较小（相对于波长），根据线性理论，上述运动学和动力学自由水面边界条件可线性化为

1.3 水底条件

池底水平且不可渗透，在池底处，垂直于池底的流体速度分量为0。

1.4 物面条件

造波板为不可渗透的固体边界，在造波板处，垂直于造波板的流体速度分量vn等于造波板的速度。

根据波板运动可知，辐射半径r可表示为

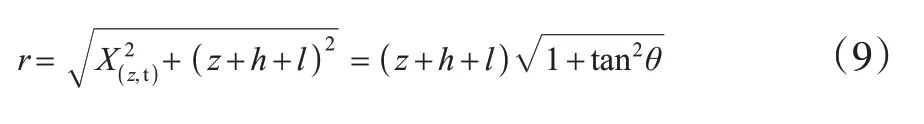
根据流体水平速度和垂向速度（u,w），可得垂直于波板的流体速度也可表示为

造波板的位置可由造波板冲程X0(t)来表示X(z,t)=f(z)X0(t)，假设造波板冲程相较于板长是极小的，则X0/(h+l)=tanθ≪1,采用小角度近似方法[6]，则

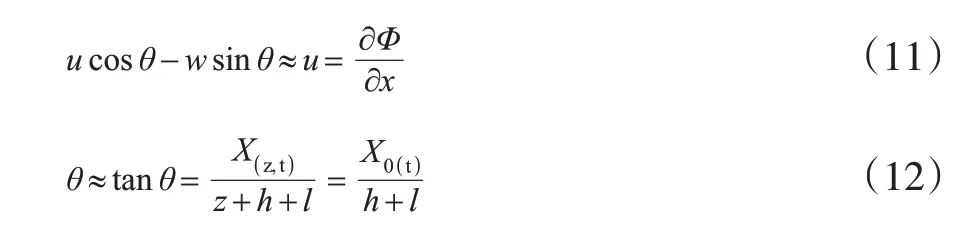
将式（9）～（12）代入式（8）中，得造波板处边界条件为

采用分离变量法分离速度势时间因子，利用控制方程和边界条件求解速度势分量，则可计算得到速度势的表达式如下，考虑到造波板处物面条件，将线性条件下造波机问题的速度势解表达为复数形式[7]。

定义C0和Cn为传递函数，传递函数是造波机冲程与波浪幅值的比值，它代表着造波系统中输入与输出之间的关系[8]。传递函数的特性决定了系统对输入信号的响应特性。传递函数的取值与造波板类型、水深、铰链深度和波浪周期相关，利用式（16）和式（17）中传递函数的解析表达式求解传递函数值，对不同模态（即阶数n）的变化对传递函数值的影响，并在0～20阶模态下分别比较不同波浪周期、水深、铰链深度对传递函数的影响，如图2～4。

图2 不同波浪周期下传递函数随模态的变化曲线

如图2所示，固定水深为10 m、铰链深度为5 m，设置波浪周期分别为1 s、2 s、3 s、4 s，当波浪周期增大时，传递函数值下降速度增加，且出现负值。如图3所示，固定波浪周期为2 s、铰链深度为5 m，设置水深分别为5 m、10 m、15 m、20 m，随着水深的增加，低模态传递函数值减小，但在3～10 阶的较高模态下，传递函数与水深成正比。如图4所示，固定波浪周期为2 s、水深为10 m，设置铰链深度分别为5 m、10 m、15 m、20 m，一阶和二阶模态下，铰链深度越大，传递函数越小。比较结果显示，非传播模态传递函数随着波浪周期和铰链深度的变化更为明显。

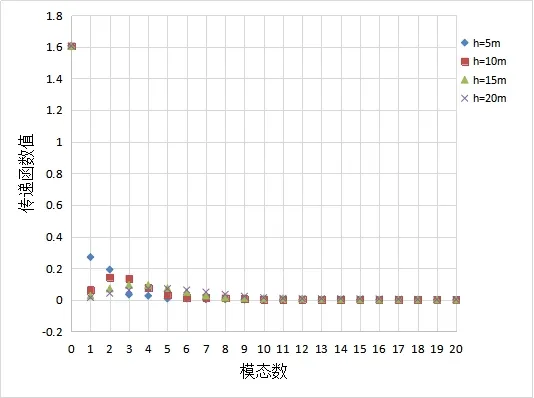
图3 不同水深下传递函数随模态的变化曲线

图4 不同铰链深度下传递函数随模态的变化曲线

当0 阶模态时，C0接近它的极限值2，随着模态数的增加，传递函数在模态数较小时下降明显，当模态大于4 阶时，其值逐渐趋近于零，即当模态为10 解以上时，非传播模态传递函数差别不大，因此在实际计算非传播模态时，取阶数为10即可满足精度要求。

2 二维波浪主动吸收理论

采用力反馈式主动吸收系统，根据造波板处的力传感器所采集到的波浪力数据，实时修正造波控制信号，以达到消除二次反射波的效果[9]。

该文主动吸收理论只研究波浪的前进模态，不考虑非传播模态。假设原始目标波速度势为Φg，运动至造波机对面的池壁或物理模型时产生与入射波周期相同、方向相反、波高衰减的反射波Φr，反射波传播到波板时再次发生反射，产生与入射波周期相同、方向相同、波高不同的二次反射波Φrr，同时对波板施加一个波浪力。假设在造波板处发生完全反射，即反射波和二次反射波在波板处形成一个反节点，二者叠加相抵消，因此在波板处物面条件仅适用于Φg。

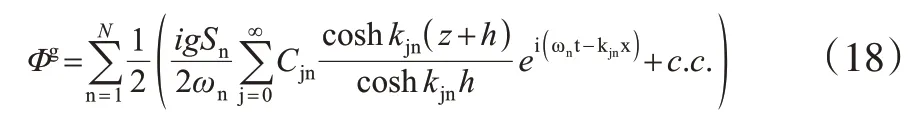
根据以上结果，可得到反射波和二次反射波，且满足水底条件和自由水面条件。

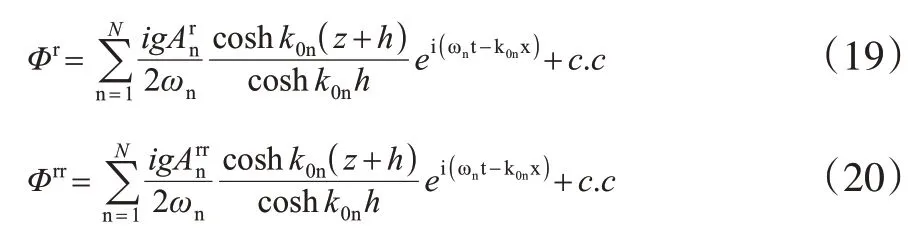
上式中An是第n个组分波浪的复振幅，c.c代表行进波的复共轭，根据之前的假设得,(n=1,2...N)。

对每一种波浪组分的三种速度势求和，且根据波板的复速度与位移幅值的关系Un=iωXn，用波板的复速度代替位移幅值。

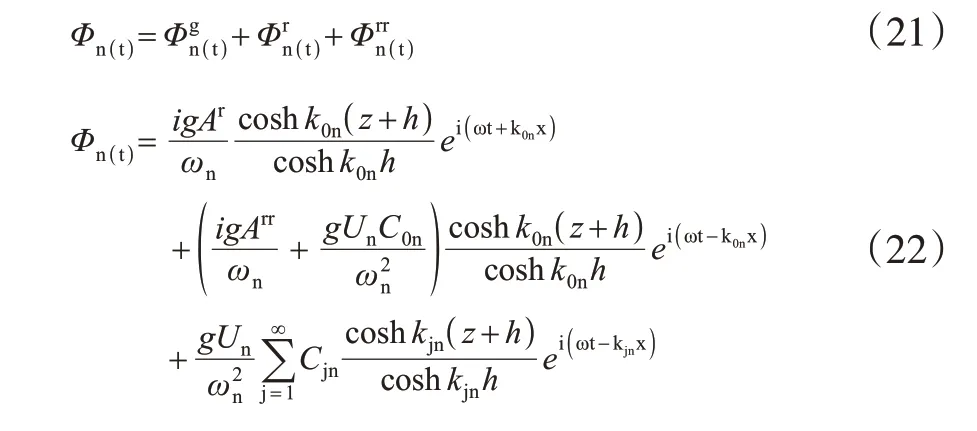
因为Φg的前进项与Φr相抵消，所以上式第二项为0，可知造波板速度与反射波、二次反射波波幅的关系

力反馈式主动吸收系统多采用干背式造波机，即在造波板背面没有池水，有利于力传感器监测造波板的受力状态，根据线性伯努利方程，整个波浪场施加给造波板的一阶压强表达式如下。

式（24）中ρ是流体的密度，等式右边第一项为非定常项，该项产生一阶动压；第二项为流体水静力项，该项产生一个恒定的静压，静压通常大于动压。

对速度势取时间导数，代入式（24）中，计算在x=0处施加给波板的瞬时压强。

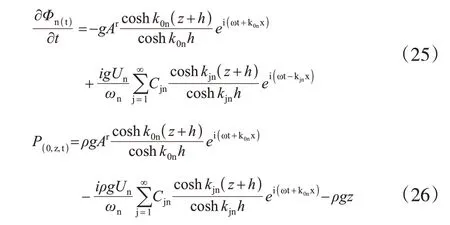
对波板表面的压强进行积分，则作用在造波板上的扭矩为

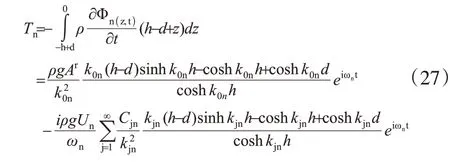
将上式中Ar用Un代替，以得到波板速度与扭矩的关系。

将n个不同组分的规则波的扭矩叠加求和，则不规则波的扭矩为

3 三维波浪主动吸收理论

3.1 斜向波

推板式和摇板式蛇形造波机都是一种分段式造波机，用于生成多向不规则波，它广泛应用于于海洋水文参数测量系统、海洋能发电装置等海洋工程装备模型样机的陆地实验及海洋科学实验。在三维无反射数值水槽中，可以很好地模拟波浪与浮体的相互作用问题[10]。三维波浪吸收理论是在二维波浪吸收理论的基础上考虑造波机布置的方向即y轴方向，根据三个三维速度势求解作用在造波板上的三维流体力。假设造波机无限宽度，不考虑造波机的边界限制。对于分段式造波机，通过控制造波机相邻板间的相位差可以产生斜向传播的波浪，计算单向的不规则波，θ为斜向波的方向[11]。

斜向浪的目标波、反射波、二次反射波的速度势形式如下。

采用与二维流体力相同的求法，可得斜向波的扭矩为

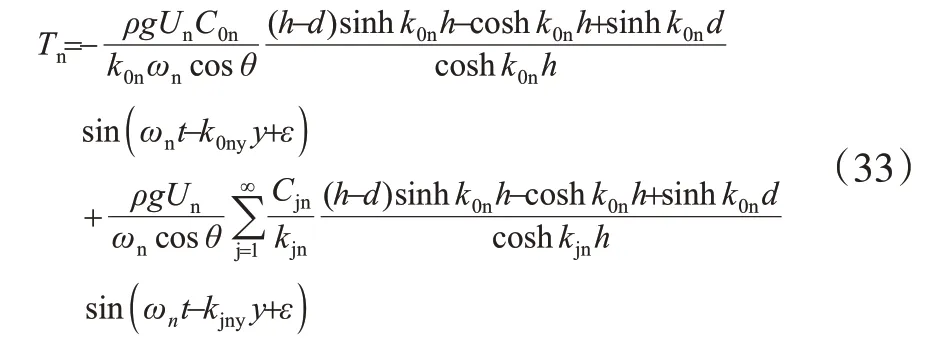
将n个不同组分的三维规则波的扭矩叠加求和，则三维不规则波的扭矩为

在斜向波浪作用下，造波板单位宽度上的动压力是空间y和时间t的周期函数。

3.2 多向波

分段式造波机每块造波板都是独立的驱动结构，都带有相同的液压伺服控制系统，整台造波机由多个子系统组成，且相对独立工作[12]。对于多向的不规则波，造波板有相位滞后εn，第n个斜向组成波的方向为θn。

根据线性叠加理论，海面上任一点处波浪可表示成不同频率和方向规则波浪的线性叠加[13-14]。将n个不同组分的三维斜向规则波的扭矩叠加求和，则三维多向不规则波的扭矩为

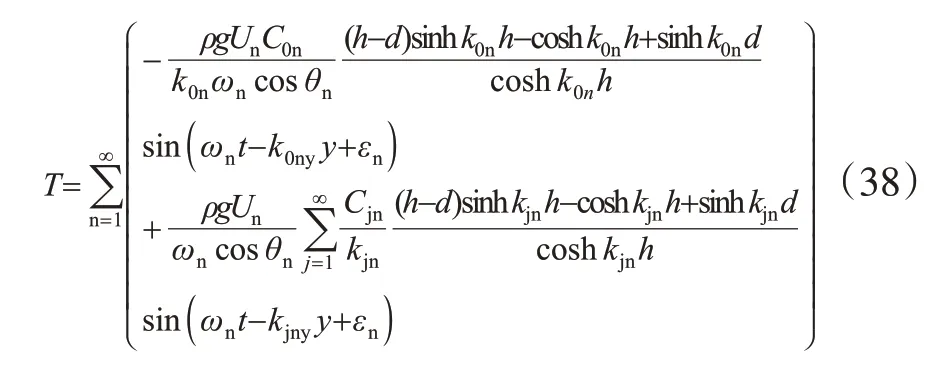
4 结语

通过分析水池波浪场中存在的3 种不同波浪成分，对摇板式造波机的力反馈式主动吸收系统进行了理论研究。基于势流理论对干背式摇板造波条件下造波板速度势解和压强的分布特性进行研究，并针对主动吸收问题，通过水动力分析，利用规则波的单频率特性和不规则波的多频率特性，得到波浪作用于造波板上的扭矩的计算方法。该文研究的单向、多向、规则、不规则波的一阶扭矩可作为开发造波机多方向吸收系统的理论基础，该理论推导将水池内波浪的运动与造波板的运动联系起来，在理论上证明了力反馈式造波机主动吸收系统对于吸收二次反射波的可行性和有效性。但是该文推导的主动吸收理论和技术主要基于一阶线性造波理论，未考虑非线性因素在二阶Stokes 波中的影响，在应对非线性波的吸收时存在局限性，未来研究基于二阶造波理论的主动吸收理论是发展方向。