三相LCL并网逆变器无参数滑模预测控制策略
郭磊磊,郑铭哲,李琰琰,朱 虹,金 楠
三相LCL并网逆变器无参数滑模预测控制策略
郭磊磊1,郑铭哲1,李琰琰1,朱 虹2,金 楠1
(1.郑州轻工业大学电气信息工程学院,河南 郑州 450002;2.中国能源建设集团安徽省电力设计院有限公司,安徽 合肥 230601)
常规三相LCL并网逆变器模型预测电流控制方法存在计算量大、参数鲁棒性差等缺点。为了解决这些问题,提出了一种三相LCL并网逆变器无参数滑模预测电流控制方法。该方法利用滑模控制理论,建立了一种新型无参数电流控制价值函数,无需采用模型参数即可实现并网电流预测控制,从而简化了控制系统的预测过程。此外,该方法省去了逆变器侧电流传感器和电容电压传感器,节约了硬件成本,提高了系统运行可靠性。最后,根据常规模型预测电流控制和滑模预测电流控制的优点,提出了一种三相并网逆变器自适应预测控制方法,提高了并网逆变器控制对模型参数失准的适应能力。实验结果表明,在系统参数失准的情况下,所提出的控制策略具有更小的并网电流控制误差,有效地提高了系统参数鲁棒性。
并网逆变器;滑模预测控制;鲁棒性;价值函数;无参数
0 引言
近年来,随着新能源并网装机容量的逐渐增大,作为新能源与电网之间接口的LCL型三相逆变器受到广泛的关注和研究[1-4]。特别是,并网逆变器输出电流的高性能控制,对提高新能源并网发电系统的电网稳定性具有重要意义[5-7]。
在逆变器控制策略中,如PI双闭环控制[8]、自抗扰控制[9]、滑模变结构控制[10]、模型预测控制(Model Predictive Control, MPC)[11-13]等控制方法已逐渐发展成熟。其中,MPC因其原理简单、可实现多目标优化控制、无需PI控制器和PWM调制模块而在LCL型并网逆变器中得到研究和应用。文献[14]提出了基于不同价值函数设计的模型预测电流控制方法,实现了网侧电流的直接预测控制。文献[15]提出一种低损耗的并网逆变器双矢量模型预测电流控制方法,提高了并网逆变器运行效率。文献[16]通过对权重因子的合理设计,建立了一种多目标混合代价函数,实现了电网电流的精确跟踪。
由于三相并网逆变器的控制性能对参数的准确性要求较高,因此,许多学者就如何提高系统控制参数的鲁棒性展开了相关研究。文献[17]针对三相两电平逆变器,分析了模型参数的不确定性对电流控制误差的影响。为了增强系统的稳定性,文献[18]提出了一种误差在线补偿策略。但是这类方法误差补偿范围受限,很难实现预测误差的精确补偿。文献[19-20]通过引入电感参数辨识算法,有效地提高了系统的参数鲁棒性。然而该算法执行较为复杂,增加了控制系统的计算负担。文献[21-22]分别提出了一种自适应控制策略,在模型参数失配的情况下能够显著减小稳态误差,具有良好的稳态性能,但是这类方法的系统设计仍较复杂。为了避免MPC对参数的依赖性,近几年,无模型预测控制成为功率变换器领域的研究热点。文献[23]提出了一种无模型预测电流控制方法,无需依赖任何模型参数,具有较强的参数鲁棒性,但该方法对系统的处理器要求较高,且计算量较大。文献[24-25]利用超局部模型的思想,设计了一种根据系统的输入和输出数据进行不断调整的动态预测模型。这种方法的缺点是需要对预测模型的控制参数进行设计。为此,文献[26]在超局部模型结构的基础上研究了一种基于扩张状态观测器的无模型电流预测控制方法,需要调整的控制参数更少,具有优越的控制性能,然而该方法目前只是在低阶滤波电路中得到了应用,并且对状态观测器的性能要求较高。
针对上述问题,本文根据滑模控制理论[27-28],研究了一种LCL型三相并网逆变器无参数滑模预测电流控制方法,所设计的新型无参数滑模预测价值函数,无需任何模型参数即可实现并网电流的预测控制,具有较强的参数鲁棒性。实验结果验证了所提方法的有效性。
1 常规LCL型并网逆变器MPC

图1 LCL型并网逆变器的典型拓扑结构
根据基尔霍夫电压电流定律,建立三相LCL型并网逆变器的数学模型,如式(1)所示。
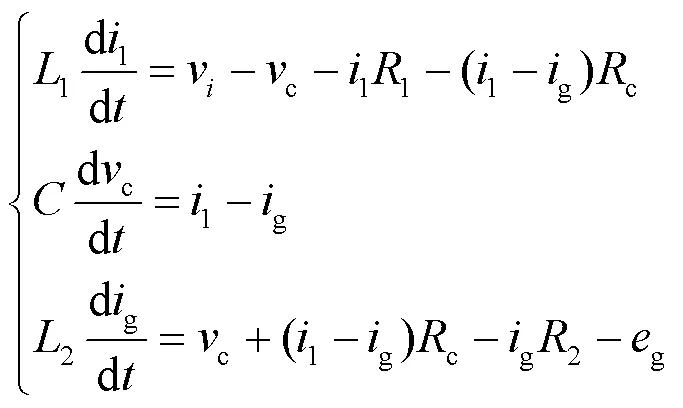
该电路模型中的电压、电流变量可以从相应的三相电压和电流中经Clark变换得到,并用复向量表示为

对式(1)采用前向欧拉离散化方法,可以得出如下方程:

式中,为采样周期。

这些开关信号确定了三相并网逆变器输出电压的值,采用矢量表示法,可由式(5)定义。


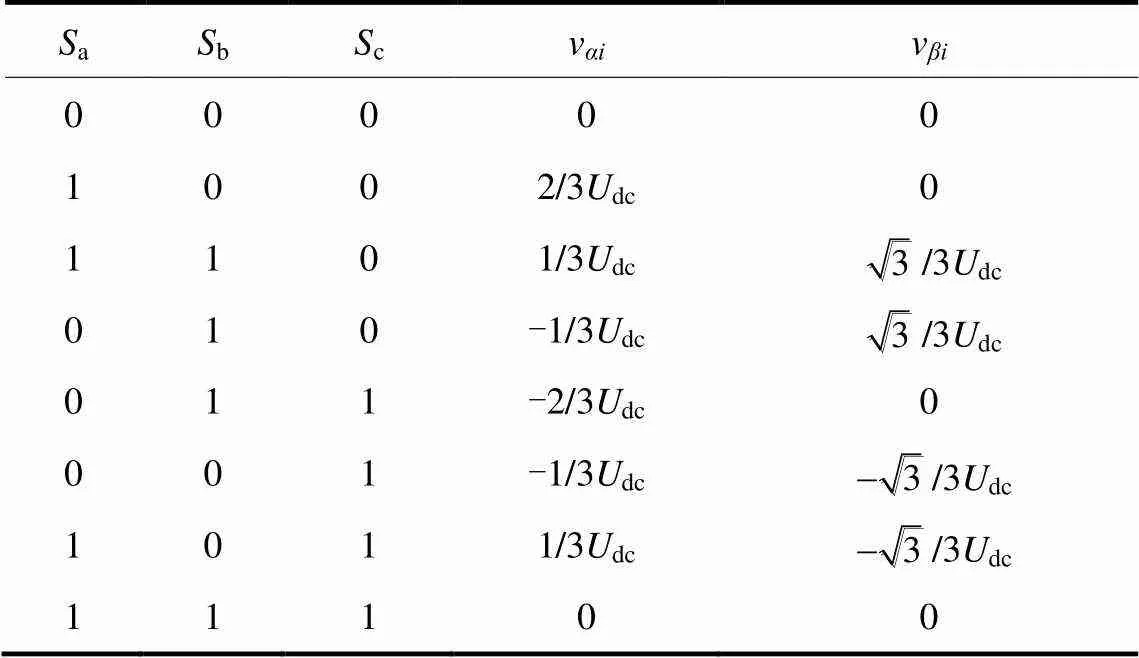
表1 电压矢量值
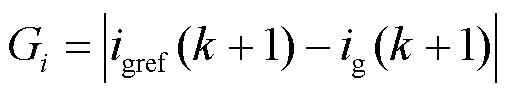

图2给出了三相LCL并网逆变器模型预测电流控制算法的流程图。
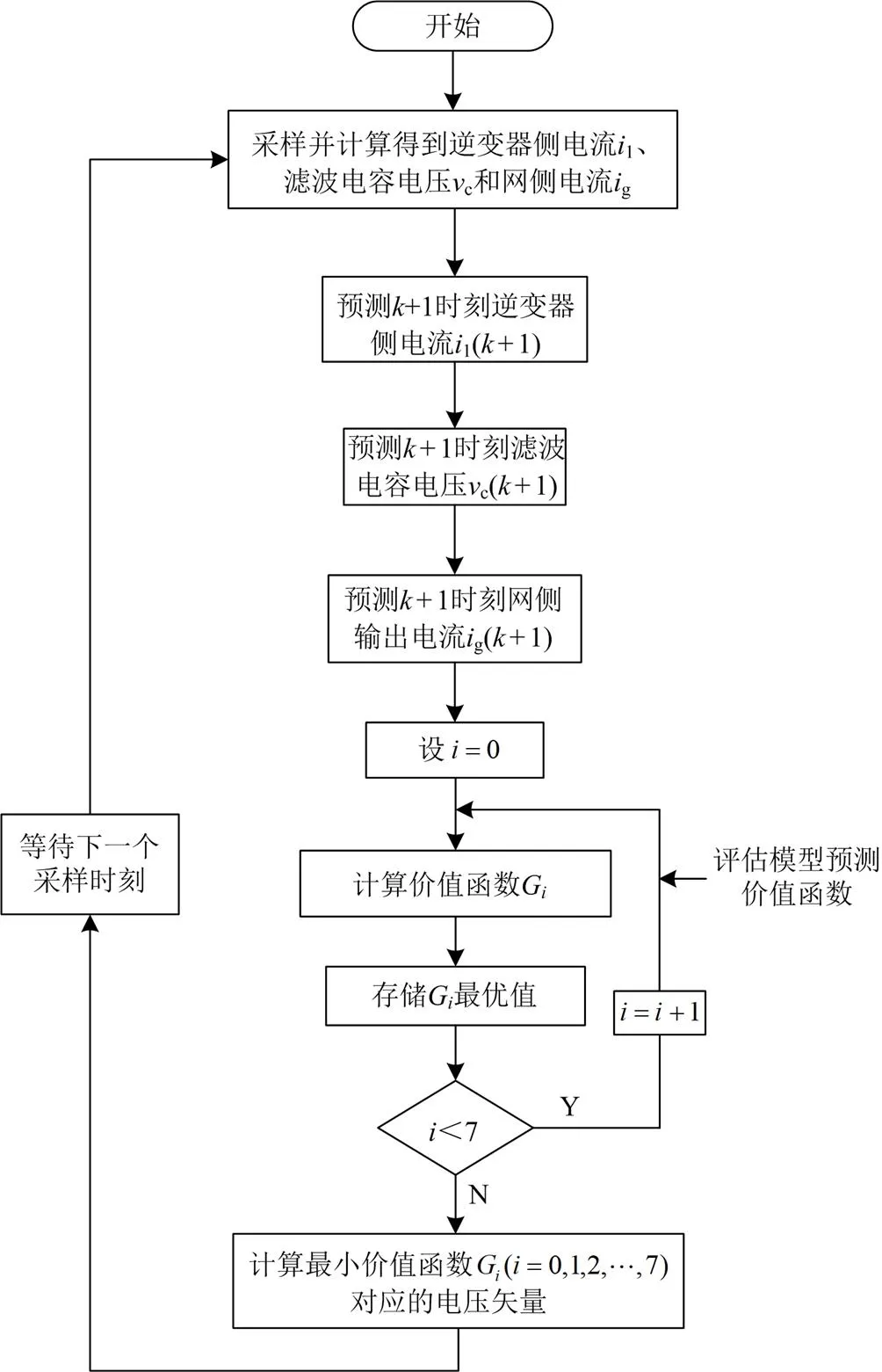
图2 模型预测电流控制流程图
2 三相LCL并网逆变器滑模预测电流 控制
考虑到LCL电路是一个三阶滤波器,其系统控制变量的动稳态特性与滤波器模型参数的精确度紧密相关,一旦模型参数失准,将恶化模型预测电流控制的动稳态控制性能。另外,在进行网侧电流的预测控制计算时,所采用的电压电流传感器较多,这会降低系统运行的稳定性。因此,为了避免模型参数变化对并网电流的影响,本文在满足并网要求的基础上利用滑模控制理论建立了一种新的价值函数,从而简化了系统预测模型,减小了滤波器模型参数的影响,提高了系统控制的鲁棒性。
2.1 无参数滑模预测系统结构
滑模预测控制不同于传统的滑模变结构控制,它的主要设计思想是利用滑模控制理论建立一种新型的滑模预测价值函数。该函数具有较强的参数鲁棒性,实现方法简单,对并网逆变器控制系统具有良好的适应性。三相LCL并网逆变器模型预测电流控制对模型参数的变化比较敏感,其系统的控制性能容易受到外界环境变化而导致模型参数失准的影响。基于上述考虑,本文对LCL型三相并网逆变器进行滑模预测控制设计,从而实现并网电流的鲁棒预测控制。LCL型三相并网逆变器无参数滑模预测控制系统结构如图3所示。

图3 LCL型三相并网逆变器无参数滑模预测控制框图

2.2 并网电流滑模预测价值函数设计
由于三相LCL并网逆变器系统控制的主要目标是网侧输出电流,因此,本文根据滑模控制理论构建一种基于滑动面的并网电流预测价值函数,然后,通过对所提出的价值函数进一步优化,减轻了选择最优电压矢量时的计算负担。
滑模控制器执行的主要任务是迫使系统控制对象沿滑模面进行平稳运行,实现对目标的精准控制。为了使控制目标运行在滑动面上,需要满足式(8)的条件。

式中:是滑动面,是相对于时间的微分。



为了保证所建立的目标变量能够运行在滑动平面上,其充分必要条件为

然而,为了得到最优的开关状态控制并网逆变器,滑模预测控制同样需要选择合适的电压矢量。因此,建立了一种基于滑动面的价值函数,如式(11)所示。
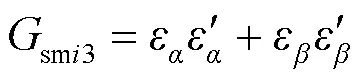
为了简化式(11),首先对所定义的滑动面进行微分计算,如式(12)所示。
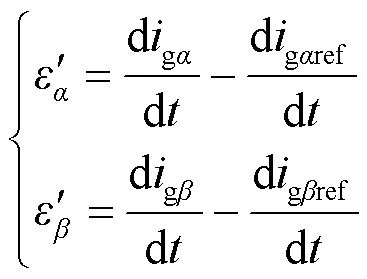

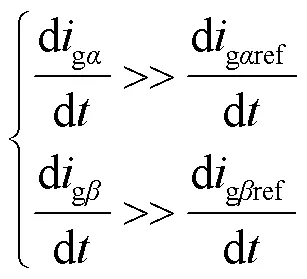
根据式(11)、式(12)所提出的滑模预测价值函数可进一步简化为
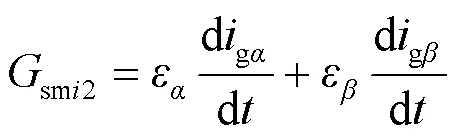
由于(1)中已经建立了三相LCL型并网逆变器的负载电路方程,在此基础上进一步化简,推导出网侧输出电流微分方程,可表示为

因此,式(14)可改写为
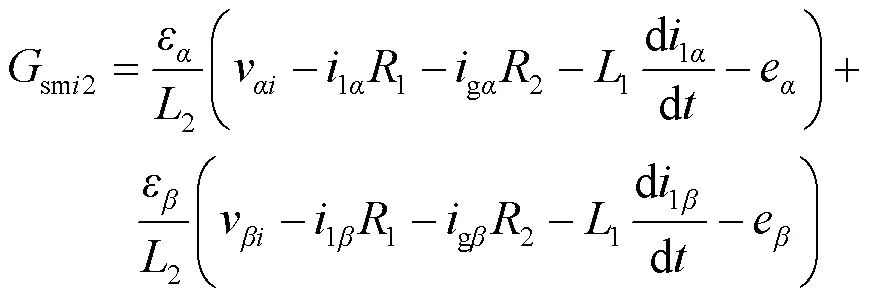
式(16)仍比较复杂,考虑到所建立的新型价值函数是为了选择最优的电压矢量,因此可进一步简化以提高系统运行的稳定性,减少计算负担。



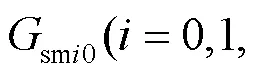
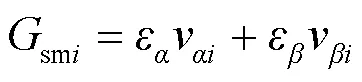
并网电流滑模预测控制流程如图5所示,所提方法首先采样当前时刻三相并网电流,计算在静止坐标系上的电流值、,然后代入到并网电流滑模预测价值函数,通过比较8个电压矢量所对应的8个价值函数的值,选择最小的价值函数所对应的电压矢量作为最优电压矢量,并将其用于控制三相LCL并网逆变器。
2.3 并网电流预测算法原理分析




2.4 三相并网逆变器自适应预测控制方法
根据上述预测原理描述,可以发现当模型参数匹配时,滑模预测控制所选择的最优电压矢量不一定是常规MPC方法中使参考电流与预测电流的误差最小时的电压矢量,这就会使滑模预测控制电流的THD稍大于常规MPC方法。当模型参数失准时,常规MPC方法容易受到模型参数变化的影响,电网电流误差会增大,而滑模预测控制方法不受参数变化的影响,具有较强的参数鲁棒性。
因此,本文结合两种控制方法的优点,进一步提出了一种三相并网逆变器自适应预测控制方法。该方法根据稳态电网电流误差自适应选择常规MPC控制和本文所提无参数滑模预测控制方法,从而确保了在参数准确和失准的情况下都能实现电流误差最小化控制。实验研究证明了三相并网逆变器自适应预测控制方法的有效性。
3 实验结果
为了验证所提出的LCL并网逆变器无参数滑模预测控制策略的有效性,搭建了基于PE-Expert4控制器和Typhoon602 +仿真器的实验平台,如图7所示。其中控制算法在由DSP和FPGA控制芯片组成的PE-Expert4处理器上执行。实验平台所用参数见表2。

图7 实验平台

表2 系统参数

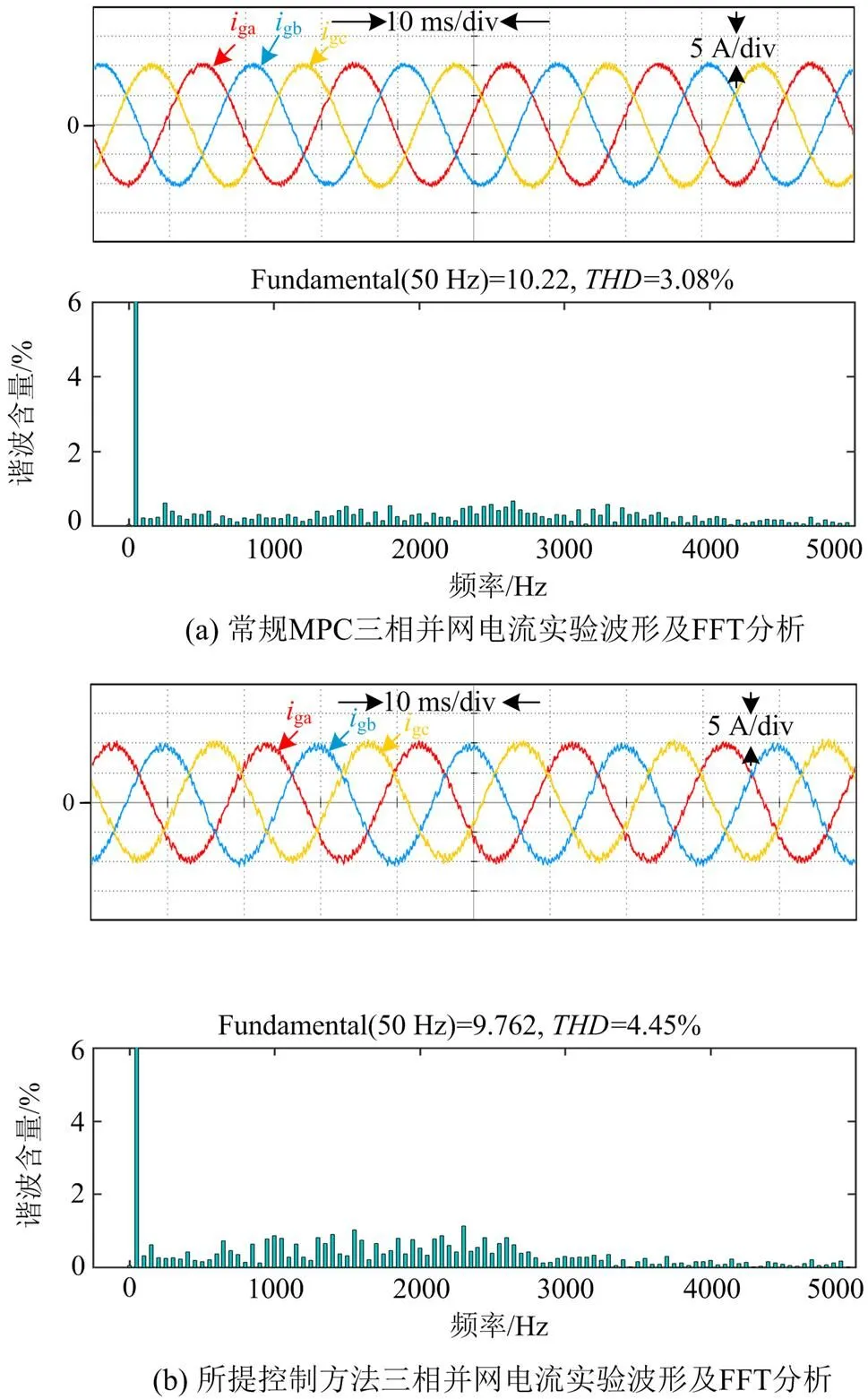
图8 三相并网电流实验对比

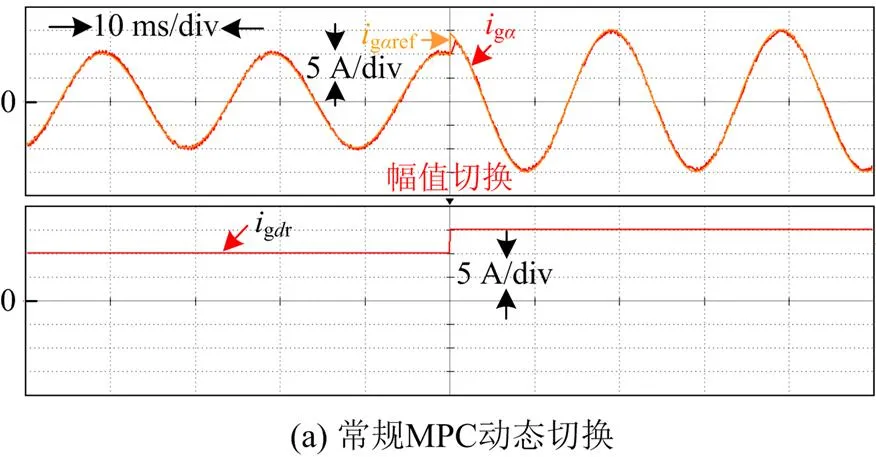
从图10可以看出,在系统模型参数失准的情况下,常规的MPC方法的电流误差较大,而本文通过采用无参数滑模预测并网电流控制方法,当模
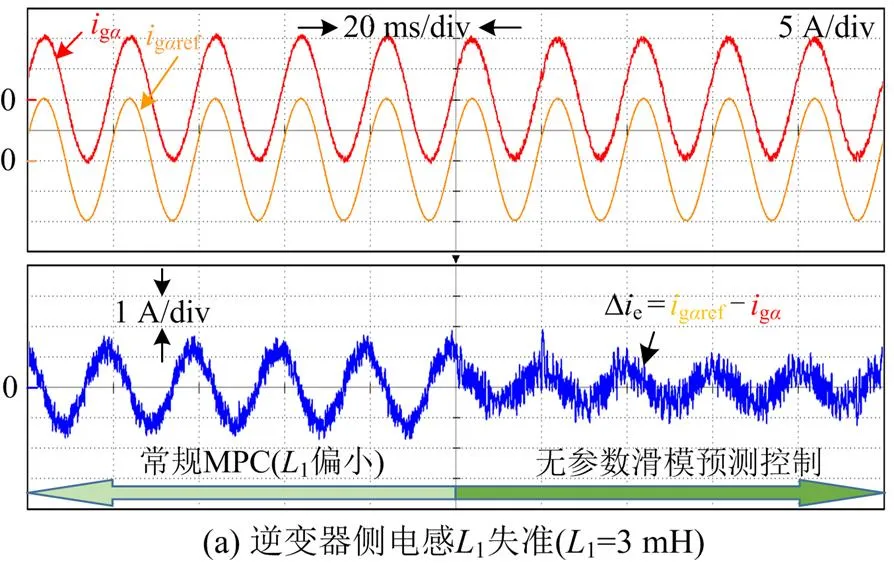
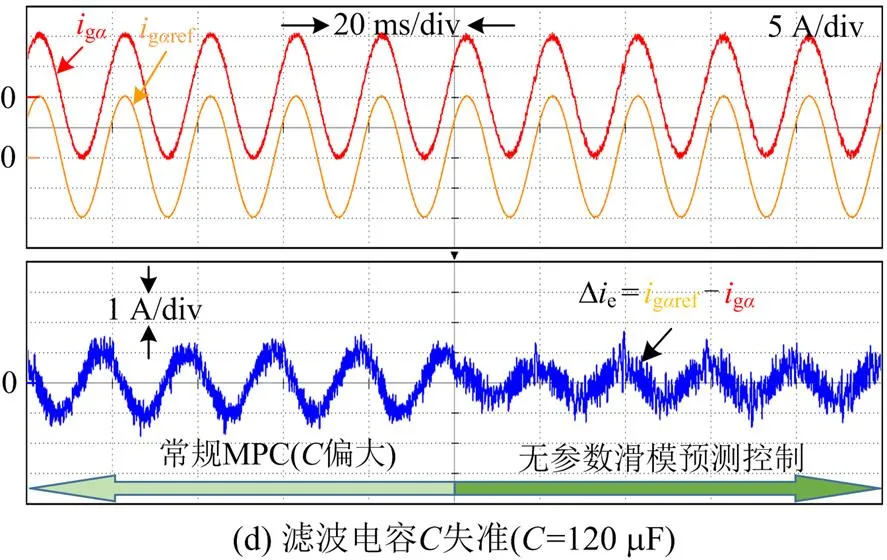
型参数失准时,其并网电流控制误差相对较小。另外,表3给出了稳态电流误差有效值的对比结果,可以发现常规MPC控制方法下的稳态电流误差有效值最大达到1.50 A,而本文所提出的滑模预测控制方法下的稳态电流误差有效值最大为0.74 A,对于稳态电流误差有效值波动范围而言,常规MPC控制方法的波动范围为0~0.58 A,而本文所提方法的稳态电流误差有效值波动范围控制在0~0.1 A。这说明了常规MPC控制方法受模型参数变化的影响较大,而本文所提出的滑模预测控制方法稳态电流误差较小,且几乎不受模型参数变化的影响,体现了该方法具有较强的参数鲁棒性。从两种控制算法的执行流程可以看出,本文设计方法不需要使用预测模型,减少了系统计算负担,进一步验证了所提方法的有效性。
由上述实验分析和验证可知,当模型参数失准时所提出的无参数滑模预测控制策略具有较强的参数鲁棒性。然而,与常规的模型预测电流控制策略相比,所提出的控制方法电流谐波含量稍大。因此,考虑到两种控制方法的特点,本文研究了一种三相并网逆变器自适应预测控制方法。在实际应用中,该方法根据稳态电网电流误差自适应选择常规的模型预测电流控制和无参数滑模预测控制,其控制思想是:当模型参数匹配时,系统以常规MPC的方式运行;当模型参数失准时,电网电流误差增大,此时系统以滑模预测控制方式运行。
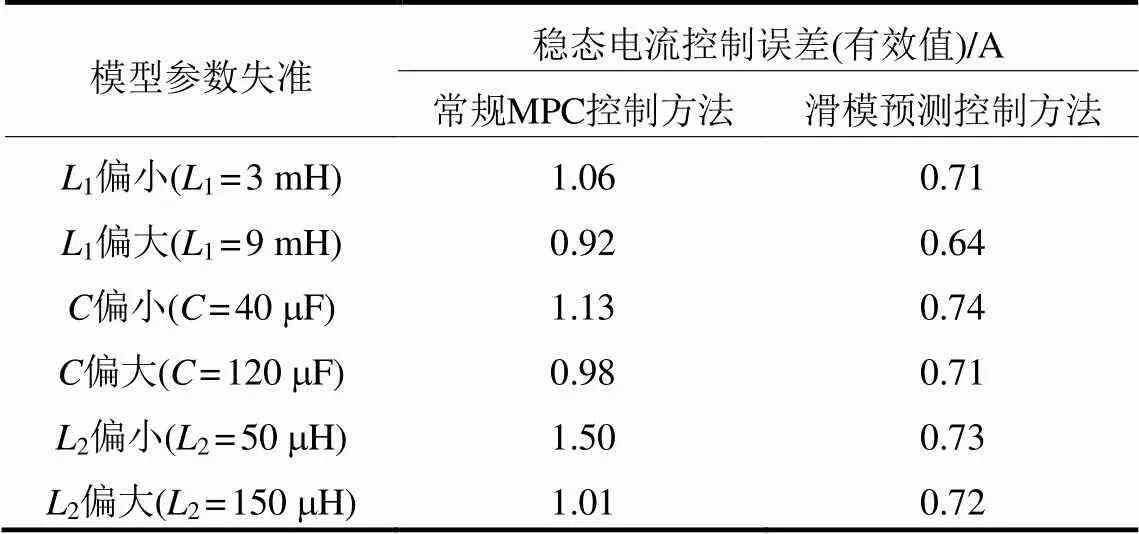
表3 稳态误差测试结果
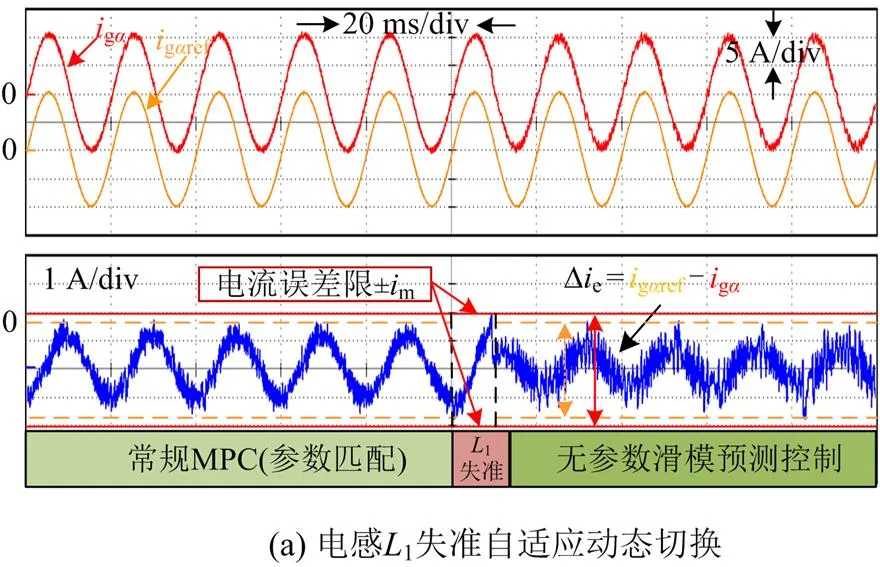
为了验证所设计自适应预测控制方法的有效性,本文通过实验测试了参数失准时的自适应预测控制的动态性能。图11(a)给出了电感失准()时的自适应预测控制动态切换波形。其中,为系统实时检测的相并网电流误差,m为并网电流误差限,这里设定。当并网电流误差满足时,系统进行并网逆变器预测控制的自适应切换。当模型参数匹配时,可以看出常规MPC控制方法下的并网电流误差波动范围为±1.5 A,当电感突然失准时,其并网电流误差,即达到了并网电流误差限,那么并网逆变器控制系统就会自动切换为滑模预测电流控制。切换后系统以滑模预测控制方式运行,其并网电流控制误差波动范围减小至±1.3 A,小于参数失准时的常规MPC控制方法电流误差,即满足。
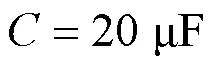
由实验分析可知,当模型参数匹配时,三相并网逆变器执行常规MPC方法,具有良好的静态性能。然而,在模型参数失准的情况下,三相并网逆变器控制系统对电流误差大小进行判定,当并网电流误差达到电流误差限时,系统就会自动切换为滑模预测电流控制。这在一定程度上增强了三相LCL并网逆变器预测控制的抗干扰能力,同时电网电流的质量也得到了提高。
4 结论
本文利用滑模预测控制理论,提出了一种三相LCL并网逆变器无参数滑模预测电流控制方法,其关键点是新型无参数滑模预测价值函数建立方法。本文详细分析了滑模预测电流控制的基本原理,通过对并网电流系统模型进行简化,得出滑模预测并网电流价值函数。所建立的价值函数可以实现LCL型三相并网逆变器网侧输出电流的无参数鲁棒预测控制。此外,考虑到当模型参数匹配时,常规MPC方法具有较小电流谐波含量的特点,研究了一种三相并网逆变器自适应预测控制方法,提高了并网逆变器对模型参数失准的适应能力。实验结果表明,所提出的并网逆变器自适应预测控制策略能够在模型参数变化时自动切换为滑模预测电流控制,切换后的无参数滑模预测控制方法能够消除常规MPC对参数的依赖性,有效增强参数失准时的并网电流跟踪性能,并且减小了控制系统的计算量,具有较好的控制效果。
[1] 许津铭, 谢少军, 张斌锋. 分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J]. 中国电机工程学报, 2015, 35(16): 4153-4166.
XU Jinming, XIE Shaojun, ZHANG Binfeng. Overview of current control techniques for grid-connected inverters with LCL filters in distributed power generation systems[J].Proceedings of the CSEE, 2015, 35(16): 4153-4166.
[2] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50.
LEI Yaxiong, LI Jianwen, LI Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control, 2014, 42(12): 44-50.
[3] 盘宏斌, 阮浩浩, 张佳乐. 基于参数化镇定控制器和误差信号 H2范数的LCL型并网逆变器电流控制方法[J]. 电力系统保护与控制, 2021, 49(4): 1-12.
PAN Hongbin, RUAN Haohao, ZHANG Jiale. A parameterized stabilizing controller and H2norm-based control scheme for LCL-filtered grid-tied inverters[J]. Power System Protection and Control, 2021, 49(4): 1-12.
[4] AGUERO J R, TAKAYESU E, NOVOSEL D, et al. Modernizing the grid: challenges and opportunities for a sustainable future[J]. IEEE Power and Energy Magazine, 2017, 15(3): 74-83.
[5] 邓翔, 胡雪峰, 龚春英. LCL滤波并网逆变电源的控制策略研究[J]. 电机与控制学报, 2011, 15(5): 37-41.
DENG Xiang, HU Xuefeng, GONG Chunying. Study on control scheme for grid-connected inverter with LCL filter[J]. Electric Machines and Control, 2011, 15(5): 37-41.
[6] 陈磊, 季亮, 杨兴武, 等. LCL型并网逆变器新型频率自适应重复控制方法[J]. 电力系统保护与控制, 2017, 45(23): 57-64.
CHEN Lei, JI Liang, YANG Xingwu, et al. A new frequency adaptive repetitive control approach for grid connected inverter with LCL filter[J]. Power System Protection and Control, 2017, 45(23): 57-64.
[7] 杨龙月, 郭锐, 张乐, 等. 非理想电网下逆变器并网电流质量改善策略[J]. 电力系统保护与控制, 2020, 48(15): 10-18.
YANG Longyue, GUO Rui, ZHANG Le, et al. Improvement strategy for grid-connected current quality of an inverter under non-ideal grid conditions[J]. Power System Protection and Control, 2020, 48(15): 10-18.
[8] 刘文军, 周龙, 陈剑, 等. LCL并网逆变器的电流双闭环控制[J]. 电力系统保护与控制, 2016, 44(17): 52-57.
LIU Wenjun, ZHOU Long, CHEN Jian, et al. Control method for grid-connected inverter with LCL filter by employing dual current closed-loops[J]. Power System Protection and Control, 2016, 44(17): 52-57.
[9] 凌毓畅, 曾江. LCL型并网逆变器的线性自抗扰控制[J]. 电气传动, 2018, 48(9): 34-41.
LING Yuchang, ZENG Jiang. Linear active disturbance rejection control for grid-connected inverter with LCL filter[J]. Electric Drive, 2018, 48(9): 34-41.
[10] KUMAR N, SAHA T K, DEY J. Sliding-mode control of PWM dual inverter-based grid connected PV system: modeling and performance analysis[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 435-444.
[11] KARAMANAKOS P, LIEGMANN E, GEYER T, et al. Model predictive control of power electronic systems: methods, results, and challenges[J]. IEEE Open Journal of Industry Applications, 2020, 1: 95-114.
[12] 任兆文, 宋书中, 黄景涛, 等. 单相三电平并网逆变器多状态模型预测控制研究[J]. 电力系统保护与控制, 2021, 49(16): 19-28.
REN Zhaowen, SONG Shuzhong, HUANG Jingtao, et al. Research on multi-state model predictive control for a single-phase three-level grid-tied inverter[J]. Power System Protection and Control, 2021, 49(16): 19-28.
[13] 游云峰, 李媛, 肖先勇, 等. 单相级联准Z源逆变器有限集模型预测控制[J]. 电力系统保护与控制, 2020, 48(1): 1-8.
YOU Yunfeng, LI Yuan, XIAO Xianyong, et al. Finite control set-model predictive control of single-phase quasi-Z-source cascaded multilevel inverter[J]. Power System Protection and Control, 2020, 48(1): 1-8.
[14] 张晓, 谭力, 鲜嘉恒, 等. LCL并网逆变器预测电流控制算法[J]. 电工技术学报, 2019, 34(增刊1): 189-201.
ZHANG Xiao, TAN Li, XIAN Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 189-201.
[15] 郭磊磊, 晋玉祥, 罗魁. 改进的低损耗并网逆变器双矢量模型预测电流控制方法[J]. 电力自动化设备, 2019, 39(10): 136-142.
GUO Leilei, JIN Yuxiang, LUO Kui. Improved two- vector-based model predictive current control method for grid-connected inverter with low loss[J]. Electric Power Automation Equipment, 2019, 39(10): 136-142.
[16] XUE C, ZHOU D, LI Y. Hybrid model predictive current and voltage control for LCL-filtered grid-connected inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(5): 5747-5760.
[17] YOUNG H A, PEREZ M A, RODRIGUEZ J. Analysis of finite control-set model predictive current control with model parameter mismatch in a three-phase inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3100-3107.
[18] 沈坤, 章兢. 具有建模误差补偿的三相逆变器模型预测控制算法[J]. 电力自动化设备, 2013, 33(7): 86-91.
SHEN Kun, ZHANG Jing. Model predictive control scheme with modeling error compensation for three- phase inverter[J]. Electric Power Automation Equipment, 2013, 33(7): 86-91.
[19] 张永昌, 蔡倩, 彭玉宾, 等. 带参数辨识功能的三电平变换器高效模型预测控制方法[J]. 电气工程学报, 2018, 13(4): 1-10.
ZHANG Yongchang, CAI Qian, PENG Yubin, et al. An efficient model predictive control for three-level converters with the function of parameter identification[J]. Journal of Electrical Engineering, 2018, 13(4): 1-10.
[20] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15): 3450-3460.
LI Wei, ZHANG Yongjun, XIAO Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3450-3460.
[21] YANG Y, TAN S, HUI S Y R. Adaptive reference model predictive control with improved performance for voltage-source inverters[J]. IEEE Transactions on Control Systems Technology, 2018, 26(2): 724-731.
[22] 满灿, 王宝华. LCL型三相并网逆变器自适应控制策略及其参数设计[J]. 电力系统保护与控制, 2017, 45(14): 134-142.
MAN Can, WANG Baohua. Adaptive control strategy and its parameters design of grid-connected inverters with LCL filter [J]. Power System Protection and Control, 2017, 45(14): 134-142.
[23] 金涛, 沈学宇, 苏泰新, 等. 三电平逆变器的改进无模型预测电流控制[J]. 电力自动化设备, 2019, 39(4): 86-91.
JIN Tao, SHEN Xueyu, SU Taixin, et al. Improved model-free predictive current control for three-level inverter[J]. Electric Power Automation Equipment, 2019, 39(4): 86-91.
[24] ZHOU Y, LI H, LIU R, et al. Continuous voltage vector model-free predictive current control of surface mounted permanent magnet synchronous motor[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 899-908.
[25] LIU X, ZHANG Y, YANG H, et al. Model-free predictive current control for three-phase power converters with LCL filter[C] // 2020 IEEE Energy Conversion Congress and Exposition (ECCE), October 11-15, 2020, Detroit, MI, USA: 5916-5921.
[26] ZHANG Y, JIN J, HUANG L. Model-free predictive current control of PMSM drives based on extended state observer using ultra-local model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[27] 张黎, 丘水生. 滑模控制逆变器的分析与实验研究[J]. 中国电机工程学报, 2006, 26(3): 59-63.
ZHANG Li, QIU Shuisheng. Analysis and experimental study of sliding mode control inverter[J]. Proceedings of the CSEE, 2006, 26(3): 59-63.
[28] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418.
LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418.
Nonparametric sliding mode predictive control strategy for a three-phase LCL grid-connected inverter
GUO Leilei1, ZHENG Mingzhe1, LI Yanyan1, ZHU Hong2, JIN Nan1
(1. College of Electrical and Information Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China; 2. China Energy Engineering Group Anhui Electric Power Design Institute Co., Ltd., Hefei 230601, China)
The disadvantages of the conventional model predictive current control method for a three-phase LCL grid-connected inverter are the need for much calculation and poor parameter robustness. To help eliminate these issues, a nonparametric sliding mode predictive current control method for a three-phase LCL grid-connected inverter is proposed. This method uses the sliding mode control theory to establish a novel nonparametric current control cost function. This can realize grid current predictive control without using model parameters, and simplify the prediction process of the control system. Also, this method eliminates the inverter side current and capacitor voltage sensors, saves hardware cost and improves the operational reliability of the system. Finally, from the advantages of conventional model predictive current control and sliding mode predictive current control, an adaptive predictive control method for a three-phase grid-connected inverter is proposed to improve the adaptability of grid-connected inverter control with model parameter inaccuracy. The experimental results show that the proposed control strategy has less grid current control error when the system parameters are inaccurate, and the robustness of system parameters is effectively improved.
grid-connected inverter; sliding mode predictive control; robustness; cost function; parameter-free
10.19783/j.cnki.pspc.211576
2021-11-22;
2022-01-13
郭磊磊(1987—),男,博士,副教授,主要研究方向为新能源功率变换器及交流电机控制技术;E-mail: 2006guoleilei@163. com
郑铭哲(1998—),男,硕士研究生,研究方向为新能源并网逆变器控制技术。E-mail: zhengmingzhe32016@163.com
国家自然科学基金项目资助(51907046,U2004166);河南省科技攻关计划项目资助(212102210021);河南省青年人才托举工程项目资助(2019HYTP021)
This work is supported by the National Natural Science Foundation of China (No. 51907046 and No. U2004166).
(编辑 姜新丽)

