基于改进秃鹰搜索算法的含分布式电源配电网分区故障定位

杨国华，冯 骥，柳 萱，陈荣达，潘 欢，杨 倩

基于改进秃鹰搜索算法的含分布式电源配电网分区故障定位

杨国华1,2，冯 骥1，柳 萱1，陈荣达1，潘 欢1,2，杨 倩1

(1.宁夏大学物理与电子电气工程学院，宁夏 银川 750021；2.宁夏电力能源安全重点实验室，宁夏 银川 750004)

为解决含分布式电源多分支配电网故障定位中存在快速性和准确性难以兼顾的问题，提出了一种基于改进秃鹰搜索算法的分区故障定位模型。首先利用Sinusoidal映射的均匀分布特性生成初始化种群，通过交叉算子、非均匀变异算子和翻筋斗觅食策略来改进秃鹰的位置更新方式，提高算法的开采和勘探能力。其次构建考虑分布式电源的开关函数和目标函数，在此基础上借鉴“黑盒方法”建立含分布式电源配电网等效分区模型，并加入定位矫正机制保障定位的准确率。最后在含分布式电源多分支配电网中进行仿真验证。与传统的秃鹰搜索算法分区定位模型相比，求解速度平均提高了30.5%，准确率平均提高了1.72%。且在不同故障位置和不同畸变点数情况下，改进秃鹰搜索算法分区定位模型均能够快速准确地定位出故障所在区段。

分布式电源；配电网；故障定位；改进秃鹰搜索算法；分区模型

0 引言

“双碳”目标的确立，极大地推动了太阳能等分布式电源(Distributed Generator, DG)的发展[1-2]。然而，大量DG接入配电网，使得故障定位求解的复杂程度不断增加，传统的故障定位方法可靠性降低[3-7]。因此，开展含分布式电源配电网故障区段定位方法研究对于促进分布式电源的发展具有重要意义[8-9]。

在配电网设备自动化升级的背景下，基于馈线终端单元(Feeder Terminal Unit, FTU)上传电流信息的故障定位方法成为当前研究的热点[10]。研究方法大致分为矩阵算法和智能算法，其中矩阵算法[11-13]是将配电网拓扑结构关系与FTU上传的电流信息结合生成故障判别矩阵，通过矩阵运算求解故障所在区段；智能算法是基于“最小故障诊断集”理论，将故障区段定位问题转换成数学优化问题，利用智能算法进行求解，如遗传算法[14-15]、仿电磁学算法[16]、粒子群算法[17-18]和天牛须算法[19]等。相比于矩阵算法，智能算法在FTU上传的故障信息受限的情况下，求解速度、定位精度仍能保持较高水平。近些年，还有不少学者根据故障电流信息的特点，引入分层分区思想[20-23]，分区故障定位模型将单次高维度计算转化为两次低维度区域定位，提高了故障定位的求解效率。

综合近年来的研究成果，虽然在定位精度、定位速度上相较于早期的定位方法均有了较大的突破，但在面对多点故障且存在多点信息畸变时，仍存在定位速度与定位精度难以兼顾的问题。对此，提出一种基于改进秃鹰搜索算法(Improve Bald Eagle Search, IBES)的配电网分区故障定位模型。利用Sinusoidal映射产生高质量初始秃鹰种群；再将交叉算子、非变异算子和翻筋斗觅食策略引入到秃鹰搜索算法上，进一步提升算法的全局、局部搜索能力，加快收敛速度；并通过建立分区定位矫正模型，达到快速准确定位故障的目的；最终通过算例仿真，验证了该模型的有效性与可靠性。

1  配电网分区故障定位模型

1.1 编码方式

将配电网中的断路器、开关视为节点，节点与节点之间的线路称为馈线区段，简称区段[24]。区段状态只包括故障与非故障两种情况，因此，这里采用0-1离散值的形式进行编码，故障时记为1，非故障时记为0。

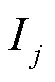
1.2 开关函数的构建

根据配电网节点和区段的编码情况，将节点至主电源途经的区段定义为节点的上游部分，记作，至DG或负载侧途经的区段定义为节点的下游部分，记作，含分布式电源配电网的开关函数常采用如式(1)所示的函数。

1.3 目标函数的选择

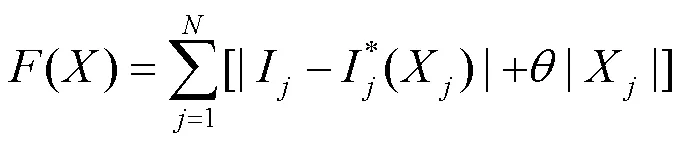
1.4 线路分区处理

以图1所示的双电源配电网为例，简要说明区域划分的依据。

图1 双电源配电网

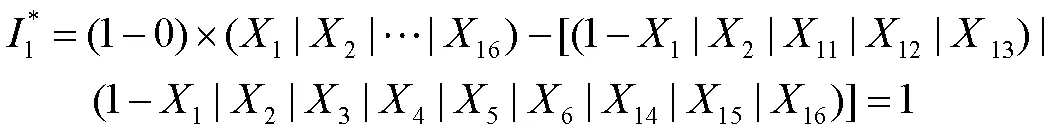
同理，区域3、区域4和区域5上节点的开关函数值为

为了消除随机性，分别验证区域2上不同区段发生故障时和发生多重故障时，区域1、区域3、区域4和区域5上所有节点的开关函数值，结果如表1所示。

由表1可知，区域2上无论发生几处故障，其他区域上所有节点的开关函数值相等。因此，区域2可以对外等效成一个“二端口网络”，同理，区域1、3、4、5均可对外等效成一个“二端口网络”[21-23]。如图2所示。

表1 不同故障情况下各区域节点开关函数值

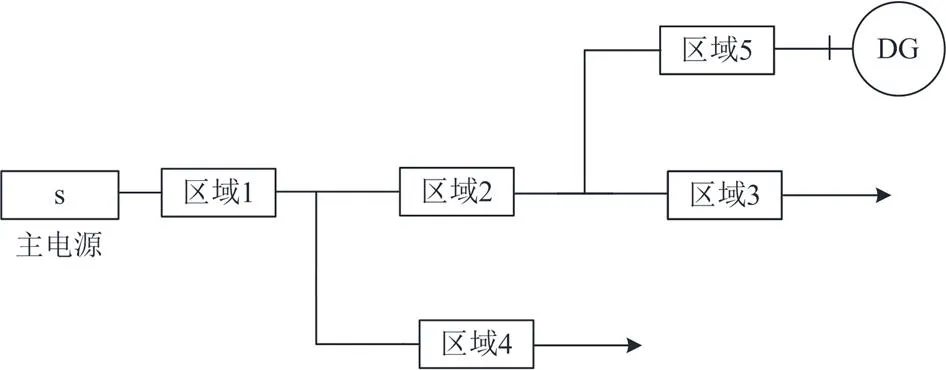
图2 配电网分区模型

等效区域构成第一层故障定位模型，区域内部节点构成第二层定位模型。等效分区模型将单次高维度的定位计算转化成了两次低维度定位计算，降低了求解维度，提高了定位速率。

2  基于IBES的故障分区定位方法

2.1 秃鹰搜索优化算法

秃鹰搜索算法(Bald Eagle Search, BES)是2020年由Alsattar等[25]提出的一种模拟秃鹰狩猎过程的搜索行为算法，该算法求解过程可以分为选择搜索空间、搜索猎物和俯冲捕获猎物3个阶段。

1) 选择搜索空间

在第一阶段秃鹰随机选择搜索空间，通过判断猎物数目来确定搜索空间内最佳狩猎区域。

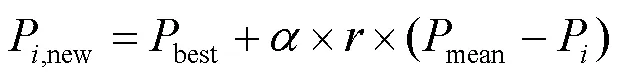
2) 搜索猎物

秃鹰在最佳搜索空间内以螺旋状移动来搜索最佳狩猎位置。搜索方式采用极坐标方程进行描述，如式(4)—式(9)所示。

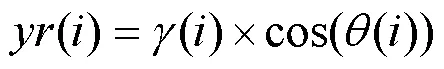
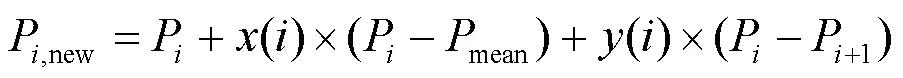
3) 俯冲捕获猎物

在这个阶段，秃鹰从所在空间的最佳位置快速俯冲飞向猎物，俯冲过程中秃鹰位置仍采用极坐标方程进行更新。

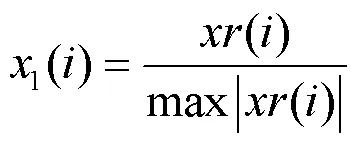
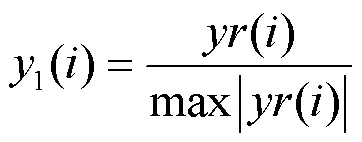
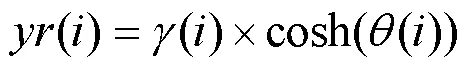
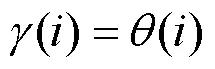
2.2 二进制的秃鹰搜索算法

区段状态值只有0或1两种情况，从而需要将秃鹰的位置用二进制的形式表示。根据文献[26] Sinusoidal映射的方式对秃鹰位置进行更新。

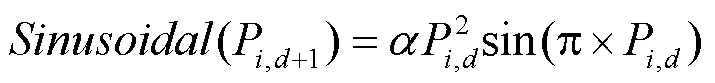
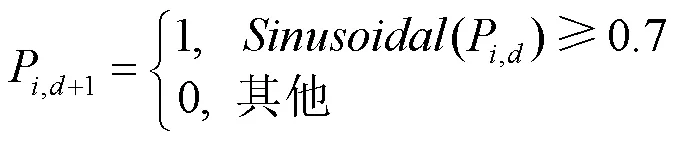
图3 Sinusoidal混沌映射

BES算法随机初始化存在种群遍历性差和种群多样性缺失等问题。为了弥补这种不足，选用Sinusoidal映射代替随机初始化，使种群在空间内的分布更均匀。

2.3 改进秃鹰搜索算法

为了提高BES算法含DG配电网分区故障定位的寻优性能，对传统BES算法做出以下改进。

改进一：由于秃鹰在选择另一个搜索区域时，会依据上个阶段的可用信息来确定下个搜索区域，如果秃鹰群体陷入局部搜索，那么在全局的搜索寻优过程中便无法准确捕获猎物。为弥补这种不足，首先通过Sinusoidal映射使秃鹰群体均匀分布于搜索空间中，一定程度上可以解决“过早收敛”的问题，再通过交叉和非均匀变异增强算法的全局探测能力。

交叉运算将秃鹰的位置互换并重新计算适应度值，当新的秃鹰位置的适应度值优于原秃鹰时则替代原秃鹰，从而增加迭代后种群个体的多样性。非均匀变异算子对秃鹰的位置进行扰动，进一步提高了种群个体的多样性，加大了秃鹰算法的搜索范围和搜索精度。非均匀变异策略对秃鹰位置进行扰动时，依次针对每个秃鹰个体随机选择个维度进行扰动，每次扰动产生的新秃鹰个体优于原秃鹰个体时则替换原秃鹰个体。

改进二：BES算法独特的螺旋飞行搜索猎物的方式具有良好的遍历性，但BES算法在迭代后期容易陷入局部最优，因此引入翻筋斗觅食策略[27]改善其局部寻优能力，提高找到最佳猎物位置的概率。

蝠鲼觅食算法具有跳出局部最优的能力，其数学模型如式(21)所示。

在每一次的翻转后，对比当前秃鹰位置与翻转之后秃鹰位置适应度值，如果此时已经陷入局部最优，则翻转后的秃鹰位置代替原秃鹰位置。与交叉、非均匀变异位置更新策略不同的是，翻筋斗觅食策略是围绕最优个体进行的，这使得算法具有更强的局部收敛性。

基于以上两处改进，提高了秃鹰搜索算法全局寻优能力和局部搜索能力。

2.4 故障定位流程

根据FTU上传的故障电流信息，提取出区域故障电流，利用IBES算法进行第一层定位，将故障定位到某个区域上，然后利用穷举法定位故障所在区段。

由于划分后的每个区域内的区段数较少，智能算法搜索的效率较低，因此采用穷举法求解故障所在区段。在此引入定位矫正机制，将IBES输出的区域定位结果代入穷举法中找出故障区段，若输出故障区段与故障区域一致则输出定位结果；若不一致，将穷举法找出的故障区段所属的区域替换IBES算法找出的故障区域，作为最终故障区域结果输出，整个定位过程如图4所示。

图4 程序流程图

3  算例分析

由于地市级的中压配电网主要是以树状多分支、多分段结构的配电网为主，因此本文选取图5所示的多分支多源配电网作为测试对象，来验证所提出模型的有效性与可靠性。其中S为系统主电源，DG1—DG3为分布式电源，DG接入区段末端且均投入运行。

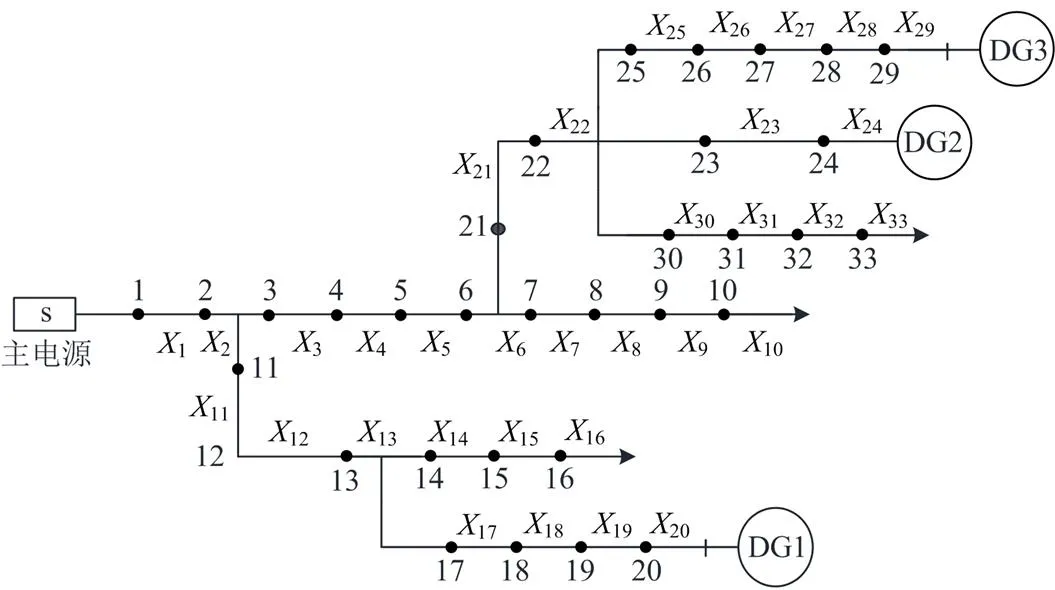
图5 33节点的含分布式电源配电网

本次实验是在Intel G4400、3.30 GHz处理器的个人计算机上运用Matlab 2018B实现仿真测试，IBES算法参数设置为：种群规模为30，最大迭代次数为50。

根据区域划分规则，将33节点的含分布式电源多分支配电网划分成10个独立区域，等效过后的配电网网络结构如图6所示。

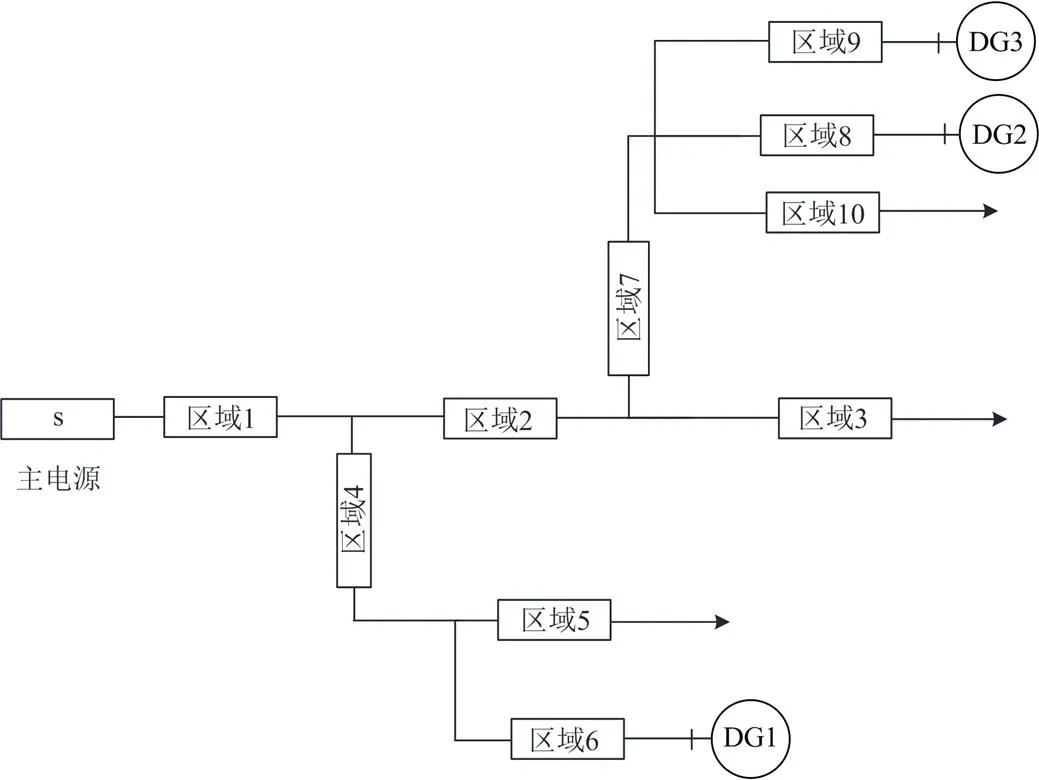
图6 33节点多源配电网分区模型

3.1 系统仿真测试分析

当区段4、18发生故障时，FTU上传的故障信息为[1,1,1,1,-1,-1,0,0,0,0,1,1,1,0,0,0,1,1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,0,0,0,0]，提取区域节点的故障电流[1,1,0,1,0,1,-1,-1,-1,0]，并利用IBES算法进行求解，运行结果如图7所示。得到的区域定位结果为[0,1,0,0,0,1,0,0,0,0]，由此判定区域二、区域六发生故障；再由穷举法找出区段内故障区段，得到的区域二、区域六内的区段状态值为[0,1,0,0]、[0,1,0,0]，即故障区段为4、18，与假定故障位置相符。

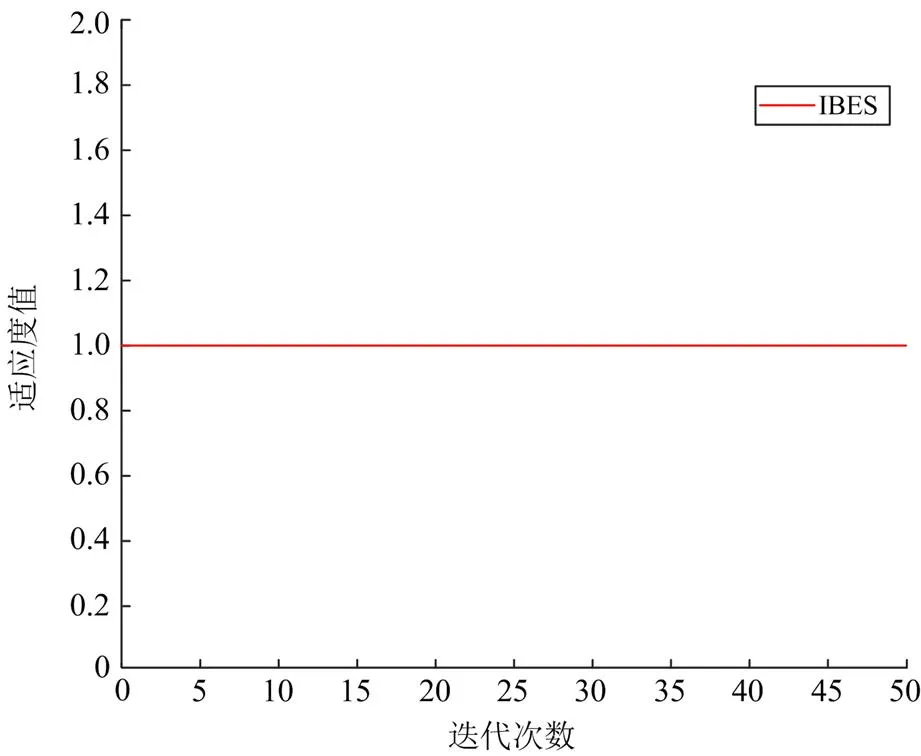
图7 无畸变信息时故障定位收敛曲线

为了更好地说明该方法具有较高的容错性，在故障节点的基础上增加信息发生畸变的情况。在故障区段9、12、22设置故障，节点3的状态从1畸变为0，节点18的状态从-1畸变为0，节点32的状态从0畸变为-1，此时寻优迭代过程中的收敛曲线如图8所示，得到的区域定位结果为[0,0,1,1,0,0,1,0,0,0]，由此判定区域三、区域四和区域七发生故障；再由穷举法找出区段内故障区段，得到区域三、区域四和区域七内的区段状态值分别为[0,0,1,0]、[0,1,0]和[0,1]，即故障区段为9、12、22，与假定故障位置相符。

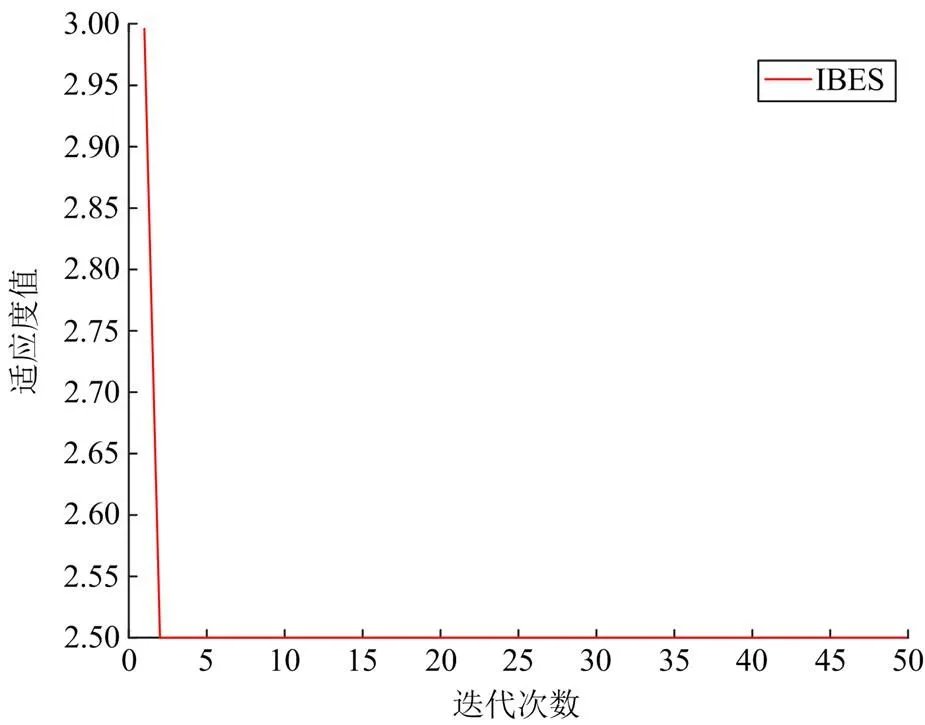
图8 节点信息畸变时故障定位收敛曲线

由图7和图8可知，在含分布式电源配电网中预设双重故障无信息畸变和三重故障存在信息畸变情况下，IBES算法分区定位模型均能够在最大迭代次数之内准确定位出故障位置，反映出IBES算法分区定位模型在多节点故障的情况下仍然可以有效地完成故障定位；同时在处理多节点故障的时候具有较强的容错能力，且在收敛速度方面也具有较大优势。

3.2 不同算法性能对比

为验证改进秃鹰搜索算法的性能优势，采用正弦与余弦算法[28](SCA)、果蝇算法[29](FFOA)和鲸鱼算法(WOA)进行对比测试，在故障区段8、18、30设置故障，节点1的状态从1畸变为0，节点4的状态从1畸变为-1，节点12的状态从1畸变为0，算法仿真对比结果如图9所示。

从图9可以发现，IBES算法在收敛速度上较WOA、SCA、FFOA算法具有明显的优势。IBES迭代3次左右即可找到最优解，WOA、SCA和FFOA能够搜索到最优解，但因其全局寻优能力较弱，分别需要22次、13次和7次迭代才能找到最优解，表明了IBES算法具良好的求解速度。

图9 算法仿真对比

将IBES算法与WOA、SCA、FFOA算法进行比较，各种方法分别运行10次，统计在不同故障位置和畸变点数情况下定位准确次数和平均迭代次数，4种算法性能对比结果如表2所示。

表2 性能对比

由表2可知，IBES算法在收敛速度上较SCA、FFOA和WOA算法都有明显提升，IBES算法相对于SCA、WOA和FFOA算法，定位准确率平均提高了43.3%、20%和6%。表明IBES算法在保障定位精度的同时也保证了收敛的速度，验证了IBES算法的优越性。

为表明改进措施的有效性，将IBES算法加分区策略与标准BES算法加分区策略和未进行分区处理的IBES算法进行对比测试，BES算法参数与IBES算法参数相同。分别运行50次，统计在不同故障位置和畸变点数情况下定位维度、定位速度和定位准确次数，结果如表3、表4所示。

从表3和表4可以看出，分区策略使每次定位维度显著减少，再加上矫正机制，大幅提升了求解速度和准确率。IBES分区模型无论在单点故障还是多点故障的情况下均能够保持较高的定位准确率，相对于未进行分区处理的改进秃鹰搜索算法，求解速度提升了84.5%，准确率平均提高了8.43%；在故障点数多且存在多点畸变情况下，未进行分区处理的改进秃鹰搜索算法求解速度较慢，准确率较差，极易陷入局部最优。与BES分区模型相比求解速度提升了30.5%，准确率平均提高了1.72%。表明IBES分区策略模型实现了精度更高、速度更快的故障区段定位，具有良好的工程实践意义。

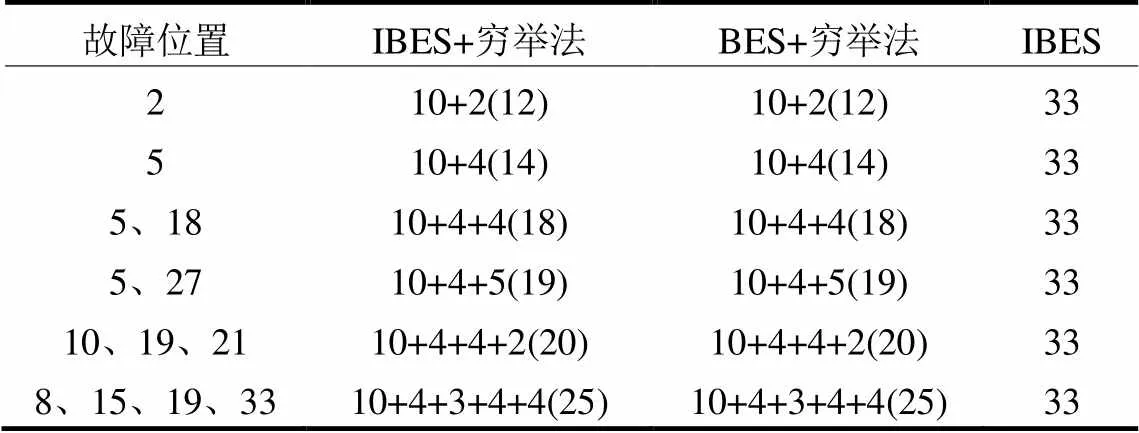
表3 定位维度的对比结果

表4 定位速度、准确性的对比结果

4  结论

针对含分布式电源多分支配电网在多点故障且多点发生信息畸变时，存在定位速度与定位精度难以兼顾的问题，本文提出了一种基于改进秃鹰搜索算法的分区故障定位模型，实现了在不同故障情况下故障点的快速精准定位。并得到以下结论：

1) 本文借鉴“黑盒方法”处理机制，将复杂配电网划分成多个简单的“二端口网络”，通过与其他定位模型对比，IBES分区模型不仅可以降低求解维度，还具有较强的容错能力。

2) IBES与SCA、FFOA和WOA相比，在收敛速度与故障定位准确性方面具有较大优势；同时相对于传统的IBES定位模型，IBES分区定位模型的求解速度和准确率分别提升了84.5%和8.43%。

3) 本文模型在多点故障且存在多点畸变情况下，与BES分区模型相比求解速度平均提升了30.5%，准确率平均提升了1.72%，充分凸显了该模型良好的定位精度和求解性能。

[1] 刘珅, 赵丽萍, 李建萍, 等. 考虑开关状态集调整的含光伏并网配电网动态故障恢复方法[J]. 电力系统保护与控制, 2021, 49(1): 24-31.

LIU Shen, ZHAO Liping, LI Jianping, et al. Dynamic fault recovery method of a photovoltaic distribution network considering switch state set adjustment[J]. Power System Protection and Control, 2021, 49(1): 24-31.

[2] 孔祥轩, 郑楚韬, 仇志成, 等. 基于广义深度学习的含DG配网故障诊断方法[J]. 电网与清洁能源, 2020, 36(11): 53-57.

KONG Xiangxuan, ZHENG Chutao, QIU Zhicheng, et al. Fault location of distribution network with DG based on GDL[J]. Power System and Clean Energy, 2020, 36(11): 53-57.

[3] JAMALI S, BAHMANYAR A, RANJBAR S. Hybrid classifier for fault location in active distribution networks[J]. Protection and Control of Modern Power Systems, 2020, 5(2): 174-182.

[4] CHEN Kunjin, HU Jun, ZHANG Yu, et al. Fault location in power distribution systems via deep graph convolutional networks[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(1).

[5] XIAO Yang, OUYANG Jinxin, XIONG Xiaofu, et al. Fault protection method of single-phase break for distribution network considering the influence of neutral grounding modes[J]. Protection and Control of Modern Power Systems, 2020, 5(2): 111-123.

[6] 于毅, 尹丽菊, 申晋, 等. 改进整数规划的含分布式电源配电网故障定位[J]. 智慧电力, 2020, 48(3): 104-108, 116.

YU Yi, YIN Liju, SHEN Jin, et al. Fault location in distribution network with distributed generation based on improved integer programming[J]. Smart Power, 2020, 48(3): 104-108, 116.

[7] 李卫国, 刘柏岑, 卢广旗. 含分布式电源的配电网单相接地故障精确定位方法[J]. 供用电, 2020, 37(9): 58-63.

LI Weiguo, LIU Baicen, LU Guangqi. A method for precise location of single-phase grounding fault in distribution network with distributed generation[J]. Distribution & Utilization, 2020, 37(9): 58-63.

[8] 程梦竹, 张新慧, 徐铭铭, 等. 基于多目标加权灰靶决策的有源配电网故障区段定位方法[J]. 电力系统保护与控制, 2021, 49(11): 124-132.

CHENG Mengzhu, ZHANG Xinhui, XUE Mingming, et al. Location method of an active distribution network fault section based on multi-target weighted grey target decision[J]. Power System Protection and Control, 2021, 49(11): 124-132.

[9] 王巍璋, 王淳, 尹发根. 基于可达矩阵和贝叶斯定理的含分布式电源的配电网故障区段定位[J]. 中国电力, 2021, 54(7): 93-99, 124.

WANG Weizhang, WANG Chun, YIN Fagen. Reachability matrix and Bayes' theorem based fault section location of power distribution network with distributed generation[J]. Electric Power, 2021, 54(7): 93-99, 124.

[10] 杨晨曦, 马杰, 杨威, 等. 基于馈线负荷骤降度的配电网故障研判方法[J]. 电力系统保护与控制, 2022, 50(2): 144-151.

YANG Chenxi, MA Jie, YANG Wei, et al. Distribution network fault location method based on the sudden drop ratio of feeder active load[J]. Power System Protection and Control, 2022, 50(2): 144-151.

[11] 魏然, 张磐, 高强伟, 等. 基于网络树状图的低压配电网故障研判仿真分析[J]. 电力系统保护与控制, 2021, 49(13): 167-173.

WEI Ran, ZHANG Pan, GAO Qiangwei, et al. Simulation analysis of low-voltage distribution network fault diagnosis based on tree structure diagram[J]. Power System Protection and Control, 2021, 49(13): 167-173.

[12] 郑晨玲, 朱革兰. 基于贝叶斯估计的配电网智能分布式故障区段定位算法[J]. 电网技术, 2020, 44(4): 1561-1567.

ZHENG Chenling, ZHU Gelan. Distribution network fault segment location algorithm based on Bayesian estimation in intelligent distributed control mode[J]. Power System Technology, 2020, 44(4): 1561-1567.

[13] 谢李为, 李勇, 罗隆福, 等. 基于距离矩阵与分支系数的配电网故障定位方法[J]. 中国电机工程学报, 2020, 40(7): 2180-2191, 2397.

XIE Liwei, LI Yong, LUO Longfu, et al. Fault location method for distribution networks based on distance matrix and branch coefficient[J]. Proceedings of the CSEE, 2020, 40(7): 2180-2191, 2397.

[14] 张莲, 宫宇, 杨洪杰, 等. 基于自适应遗传粒子群算法的配电网故障定位[J]. 重庆理工大学学报(自然科学版), 2021, 35(9): 160-168.

ZHANG Lian, GONG Yu, YANG Hongjie, et al. Fault location of distribution network based on adaptive genetic particle swarm optimization algorithm[J]. Journal of Chongqing University of Technology (Natural Science Edition), 2021, 35(9): 160-168.

[15] 孙志达, 杨涛, 吴栋萁, 等. 基于多源信息和遗传算法的配电网故障定位模型[J]. 智慧电力, 2021, 49(12): 104-110.

SUN Zhida, YANG Tao, WU Dongqi, et al. Fault location model for distribution networks based on multi-source information and genetic algorithm[J]. Smart Power, 2021, 49(12): 104-110.

[16] 吉兴全, 张朔, 张玉敏, 等. 基于IELM算法的配电网故障区段定位[J]. 电力系统自动化, 2021, 45(22): 157-166.

JI Xingquan, ZHANG Shuo, ZHANG Yumin, et al. Fault section location for distribution network based on improved electromagnetism-like mechanism algorithm[J]. Automation of Electric Power Systems, 2021, 45(22): 157-166.

[17] 赵乔, 王增平, 董文娜, 等. 基于免疫二进制粒子群优化算法的配电网故障定位方法研究[J]. 电力系统保护与控制, 2020, 48(20): 83-89.

ZHAO Qiao, WANG Zengping, DONG Wenna, et al. Research on fault location in an immune binary particle swarm algorithm[J]. Power System Protection and Control, 2020, 48(20): 83-89.

[18] 刘煜, 王俊江, 焦青, 等. 基于量子行为粒子群算法的含分布式电源的配电网故障定位[J]. 智慧电力, 2020, 48(8): 51-55.

LIU Yu, WANG Junjiang, JIAO Qing, et al. Fault location of distribution network with distributed power supply based on quantum behavior particle swarm optimization algorithm[J]. Smart Power, 2020, 48(8): 51-55.

[19] 邱彬, 罗添元, 宁博, 等. 基于BAS-IGA的含分布式电源配电网故障定位[J]. 电力系统及其自动化学报, 2021, 33(2): 8-14.

QIU Bin, LUO Tianyuan, NING Bo, et al. Fault location of distribution network with distribution generations based on BAS-IGA[J]. Proceedings of the CSU-EPSA, 2021, 33(2): 8-14.

[20] 程云祥, 李阳, 卢芳, 等. 多源信息辅助分区的主动配电网故障区段定位[J]. 电力系统保护与控制, 2020, 48(17): 147-154.

CHENG Yunxiang, LI Yang, LU Fang, et al. Fault-section location for active distribution networks assisted by multi-source information[J]. Power System Protectionand Control, 2020, 48(17): 147-154.

[21] 李明阳, 张沈习, 程浩忠, 等. 含分布式电源的主动配电网分层故障定位方法[J]. 电力系统及其自动化学报, 2021, 33(8): 79-87.

LI Mingyang, ZHANG Shenxi, CHENG Haozhong, et al. Hierarchical fault location method for active distribution network with distributed generation[J]. Proceedings of the CSU-EPSA, 2021, 33(8): 79-87.

[22] 王秋杰, 金涛, 谭洪, 等. 基于分层模型和智能校验算法的配电网故障定位技术[J]. 电工技术学报, 2018, 33(22): 5327-5337.

WANG Qiujie, JIN Tao, TAN Hong, et al. The technology on fault location of distribution network based on hierarchical model and intelligent checking algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5327-5337.

[23] 甄永琦, 蒋伟. 改进灰狼算法在配电网故障定位中的应用[J]. 计算机应用与软件, 2020, 37(11): 200-205.

ZHEN Yongqi, JIANG Wei. Application of improved grey wolf algorithm in fault location of distribution network[J]. Computer Applications and Software, 2020, 37(11): 200-205.

[24] 孔培, 刘建锋, 周健, 等. 基于整数线性规划的配电网故障定位容错算法[J]. 电力系统保护与控制, 2020, 48(24): 27-35.

KONG Pei, LIU Jianfeng, ZHOU Jian, et al. Fault-tolerant algorithm for fault location in distribution network based on integer linear programming[J]. Power System Protection and Control, 2020, 48(24): 27-35.

[25] ALSATTAR H A, ZAIDAN A A, ZAIDAN B B. Novelmeta-heuristic bald eagle search optimization algorithm[J]. Artificial Intelligence Review: An International Science and Engineering Journal, 2020, 53(8): 2237-2264.

[26] 李建美, 高兴宝. 基于自适应变异的混沌粒子群优化算法[J]. 计算机工程与应用, 2016, 52(10): 44-49.

LI Jianmei, GAO Xingbao. Chaotic particle swarm optimization algorithm with adaptive mutation[J]. Computer Engineering and Applications, 2016, 52(10): 44-49.

[27] ZHAO Weiguo, ZHANG Zhenxing, WANG Liying. Manta ray foraging optimization: an effective bio-inspired optimizer for engineering applications[J]. Engineering Applications of Artificial Intelligence, 2020, 87(1).

[28] 郭艳艳, 熊国江. 基于正弦与余弦优化算法的配电网故障区间定位[J]. 电力系统保护与控制, 2017, 45(13): 97-101.

GUO Yanyan, XIONG Guojiang. Fault section location in distribution network by means of sine cosine algorithm[J]. Power System Protection and Control, 2017, 45(13): 97-101.

[29] 王巍璋, 王淳, 敖鑫. 基于果蝇优化算法的配电网故障定位[J]. 电力系统保护与控制, 2019, 47(18): 108-114.

WANG Weizhang, WANG Chun, AO Xin. Fault location of power distribution network based on fruit fly optimization algorithm[J]. Power System Protection and Control, 2019, 47(18): 108-114.

Fault location of a distribution network hierarchical model with a distribution generator based on IBES

YANG Guohua1, 2, FENG Ji1, LIU Xuan1, CHEN Rongda1, PAN Huan1, 2, YANG Qian1

(1. School of Physics and Electronic-Electrical Engineering, Ningxia University, Yinchuan 750021, China;2. Ningxia Key Laboratory of Electrical Energy Security, Yinchuan 750004, China)

There is a problem that it is difficult to balance the speed and accuracy of fault location in a multi-branch distribution network with a distributed generator. Thus a fault location model based on an improved bald eagle search algorithm is proposed.First, this paper uses the uniform distribution characteristics of sinusoidal mapping to generate the initial population. It also improves the position update method of the bald eagle through a crossover operator, the non-uniform mutation operator and the somersault foraging strategy, and enhances the mining and exploration capabilities of the algorithm.Secondly, the switching function and objective function considering the distributed generator are constructed. An equivalent hierarchical model of a distribution network with a distributed generator is established by referring to the "black box method", and a location correction mechanism is added to ensure the accuracy of location. Finally, a simulation is carried out in the multi-branch distribution network with a distributed generator. Compared with the traditional bald eagle search algorithm zoning location model, solution speed is improved by 30.5% and accuracy is improved by 1.72% on average.In addition, under different fault locations and different distortion points, the improved bald eagle search algorithm zone location model can quickly and accurately locate the fault zone.

distribution generator;distribution network; fault location; improved bald eagle search; hierarchical model

10.19783/j.cnki.pspc.211674

2021-12-08；

2022-03-08

杨国华(1972—)，男，硕士，教授，硕士生导师，研究方向为新能源电力系统自动化技术；E-mail: ygh@ nxu.edu.cn

冯 骥(1998—)，男，通信作者，硕士研究生，研究方向为电力系统故障诊断与定位；E-mail: fj065frontile@ 163.com

潘 欢(1983—)，男，博士，副教授，研究方向为复杂电网建模与分析、新能源协同并网。E-mail: pan198303@ gmail.com

国家自然科学基金项目资助(71263043，61763040)；宁夏自然科学基金项目资助(2021AAC03062)；宁夏自治区一流基层教学组织建设项目资助(nxyljcjxz-2)

This work is supported by the National Natural Science Foundation of China (No. 71263043 and No. 61763040).

(编辑 魏小丽)