基于状态空间模型与PEM迭代算法的电力系统惯量辨识

徐 波，杨逸欣，余万强，陈雨楠，李东东

基于状态空间模型与PEM迭代算法的电力系统惯量辨识

徐 波1，杨逸欣1，余万强2，陈雨楠3，李东东1

(1.上海电力大学电气工程学院，上海 200090；2.国网四川省电力公司内江供电公司，四川 内江 641400；3.华中科技大学电气与电子工程学院，湖北 武汉 430074)

惯量是保障电力系统频率安全稳定的重要参数之一，因此需对其进行精确的在线测量。针对当前采用的系统辨识方法测量精度不高的问题，研究系统辨识中算法模型的选择对测量结果的影响。首先，分析比较现有的传递函数模型、自回归滑动平均模型以及子空间辨识模型进行惯量辨识的测量原理。其次，从惯量响应初期阶段数据匹配的角度，提出基于PEM迭代算法的状态空间估计模型。最后，搭建10机39节点电力仿真系统，验证了所提辨识模型的正确性。并在不同功率扰动程度以及不同采样时间窗口下，分析4种辨识模型的适用性，为确定系统最优辨识模型提供参考依据。

电力系统惯量；系统辨识；在线测量；迭代算法

0 引言

发展新能源是实现双碳目标的重要措施之一。随着大规模新能源接入电网，传统的同步发电机逐步被替换。由于风、光等可再生能源发电具有间歇性和波动性，且多需通过电力电子设备并网发电，导致电力系统的惯量响应能力降低。低惯量电力系统无法对扰动后频率的变化提供有效支撑，不利于系统的安全稳定运行[1-6]。因此，准确测量含高比例新能源和电力电子设备的新型电力系统的惯量具有重要意义[7-10]。

目前电力系统惯量测量的方法可分为离线测量和在线测量两类。离线测量方法基于转子运动方程，利用扰动事件后的数据进行测量。文献[11]利用扰动事件发生前后系统的功率缺额和频率变化率的改变，进行区域系统惯量值的测量评估。但离线测量方法需要等待大扰动事件的发生，只能对系统惯量进行事后测量。

在线测量方法可实现对系统惯量的连续估计测量。其实质是基于数据驱动的系统辨识方法，即通过电力系统正常运行或受到小扰动时的有功变化和频率变化数据，采用系统辨识算法建立电力系统中惯量响应模型，由此分析模型中输入、输出与系统惯量的关系，并从中求取惯量值。文献[12]通过脉冲响应、阶跃响应和最大频率变化率从已辨识的模型中求取惯性时间常数，但文中未涉及对辨识模型的准确性评价。文献[13]提出采用传递函数模型辨识网络模型，并引入了模型参数优化和奇异值分解(Singular Value Decomposition, SVD)降阶。文献[14]基于自回归滑动平均模型的系统辨识算法建立了电力系统惯量响应等效模型，从中可求得系统等效惯量。文献[15]基于子空间状态空间系统辨识的数值算法(Numerical Algorithms for State Space Subspace System Identification, N4SID)得到有功偏差和母线频率偏差之间的动态模型，并从中求得系统中同步发电机惯量。文献[16]在该算法基础上进行改进，使其能准确估计含可再生能源的系统整体等效惯量。

分析上述文献中所采用的系统辨识方法可以看出，辨识算法模型的可靠性与惯量测量结果的准确性密切相关。但是目前文献多注重提出新的辨识方法，而对在线估计方法的估计精度、辨识算法模型优劣等问题研究较少，缺乏选择最优辨识模型的参考依据。

鉴于此，本文首先分析对比目前常用的传递函数估计(Transfer Function Estimation, TFEST)模型、带输入自回归滑动平均(Auto-Regressive Moving Average with eXogenous inputs, ARMAX)模型以及N4SID模型。在此基础上，针对精度不高的问题，从数据匹配度角度考虑，本文提出将状态空间估计(State Space Estimation, SSEST)模型与PEM(Prediction Error Minimization)迭代算法结合，以实现辨识模型参数初值的迭代优化。最后在改进的IEEE10机39节点系统中仿真分析以上4种辨识模型的适用性，结果表明本文所提模型在惯量响应期间具有高拟合度，有利于惯量的准确可靠计算，并为确定系统最优拟合模型提供了建议。

1 基于系统辨识的电力系统惯量在线测量

1.1 系统等效模型辨识的测量原理

当电力系统发生扰动时，为了维持系统中功率供需平衡，电力系统会进行调频，一般可分为惯量响应、一次调频、二次调频和三次调频，如图1所示。其中，惯量响应将在扰动发生后快速动作，并持续数秒以阻碍频率变化，为系统提供惯量支撑功率，常用惯性时间常数表征惯量响应能力的大小。

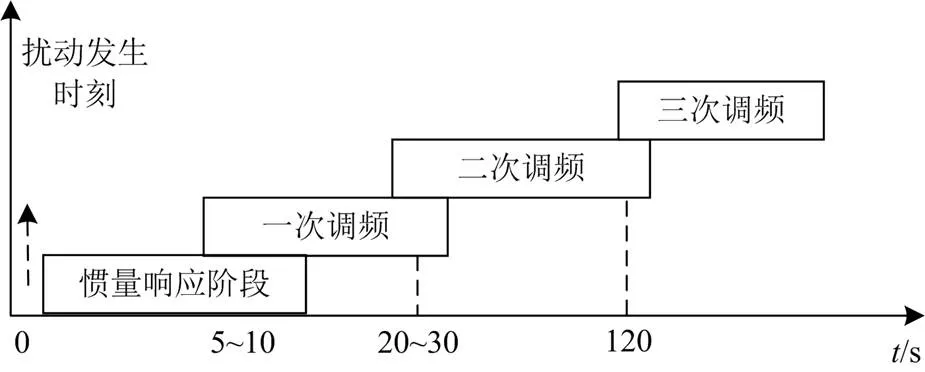
图1 调频过程

在电力系统的实际运行中，负荷不断变化，系统存在功率波动，将会引起持续的惯量响应。此时将电力系统或区域等效为一台同步发电机，并采用转子运动方程建立有功不平衡时惯性时间常数、功率与频率之间的动态关系，如式(1)所示[11]。

系统辨识作为可从噪声数据中建立复杂系统精确数学模型的主要方法之一，能够建立具有电力系统动态特点的数学模型[17-18]，其原理如图2所示。通过系统辨识算法可辨识出如式(2)所示的未知惯量响应模型，并从中获取系统惯性时间常数。

图2 系统辨识原理图

电力系统正常运行中含有多种复杂的控制环节，因此辨识得到的传递函数往往为高阶模型，受多种参数混合影响，无法直接推导出惯量值。一般情况下，可采用低阶模型辨识出电力系统等效模型，并通过对辨识模型进行降阶拟合从而对惯性时间常数进行推导。

以二阶传递函数为例。假设连续时间下辨识得到的惯量响应模型函数形式满足式(3)。

将该传递函数转变为状态空间模型。采用频域拟合的方法，在保持系统的能控性、能观性且满足稳定状态输入与输出关系的前提下，识别并消除无关量使状态空间模型的阶数降为一阶，最后将化简后的一阶状态空间模型转变为如式(4)所示的连续时间传递函数。

1.2 系统辨识在线测量系统惯量的步骤流程

基于上述原理，在线测量系统等效惯性时间常数可分为以下3个步骤：

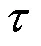
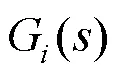
基于系统辨识的方法对电力系统的等效惯性时间常数进行在线的测量流程，如图3所示。

图3 系统辨识在线测量流程图

分析可知，系统辨识算法模型决定所辨识的电力系统惯量响应模型的准确性，进而影响系统等效惯性时间常数的测量精度。因此，选择合适的系统辨识算法模型是在线测量电力系统等效惯性时间常数的关键步骤。

2 系统辨识算法模型

目前已用于电力系统惯量测量的系统辨识模型有TFEST模型[12-13,19]、ARMAX模型[14,20-21]以及N4SID模型[15-16, 22]等。本节首先从原理上对这3种模型进行分析对比，并在此基础上从数据匹配的角度提出基于PEM迭代算法的SSEST模型。

2.1 模型原理分析

2.1.1 TFEST模型

TFEST[23-24]模型是传递函数估计模型，即用多项式之比来描述系统输入和输出之间的关系。

在连续时间内，TFEST模型的形式为

2.1.2 ARMAX模型

ARMAX模型[14]是带输入自回归滑动平均模型，采用该模型观察到的输出是包含过去的输入、噪声和随机干扰信号3个回归项的总和。不同的多项式模型都可以表示为一个通用模型的特殊情况。离散ARMAX模型的系统传递函数为

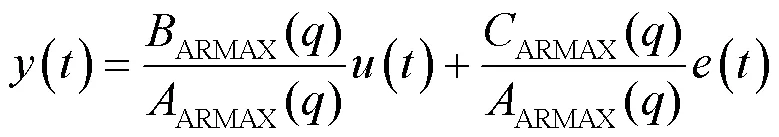
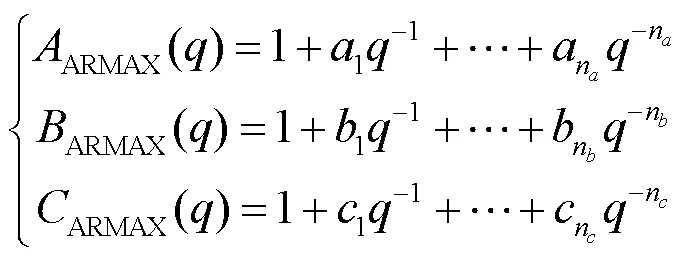
2.1.3 N4SID模型

N4SID模型[25]是数值子空间方法估计状态空间模型，用于辨识系统的状态空间模型，不需要知道系统内部联系即可实现对复杂系统的辨识。对于单输入、单输出的阶线性时不变系统，其状态空间模型表示为

2.2 模型对比

表1比较了TFEST模型、ARMAX模型以及N4SID模型辨识的适用场合及优点。

表1 系统辨识模型对比

可见，作为辨识连续时间的模型，TFSET模型具有更高的时间分辨率，但在测量噪声的占比大时，会因测量噪声影响结果精度。而N4SID模型和ARMAX模型作为辨识离散时间的模型，在辨识过程中需将离散的时间函数转变为连续的时间函数形式，即将离散模型连续化。因此采用N4SID模型和ARMAX模型虽能准确反应系统的动态模型，但会增加计算成本。而在电力系统等效惯量测量中需要低耗时和高可靠性的模型。

2.3 基于最小化PEM的SSEST模型

基于PEM算法的SSEST模型可辨识连续和离散时间下的状态空间模型，该模型采用PEM算法更新初始模型的参数以匹配估计数据，可实现初始辨识模型的再优化，便于计算和分析，能得到数据匹配度更优的模型。

SSEST模型是状态空间估计模型，可使用时域或频域的数据估计阶的连续时间状态空间模型系统，可表示为

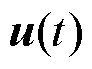
将式(11)所示的状态空间信号模型进行拉氏变换，得到传递函数：

式中，是单位矩阵。

采用连续的采样数据可构造如下规则的Hankel矩阵。

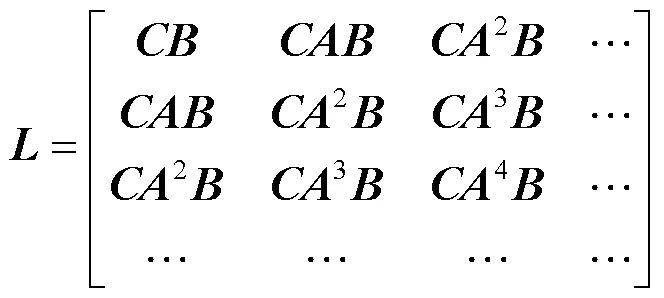
将式(13)分解为两个矩阵，如式(14)所示。

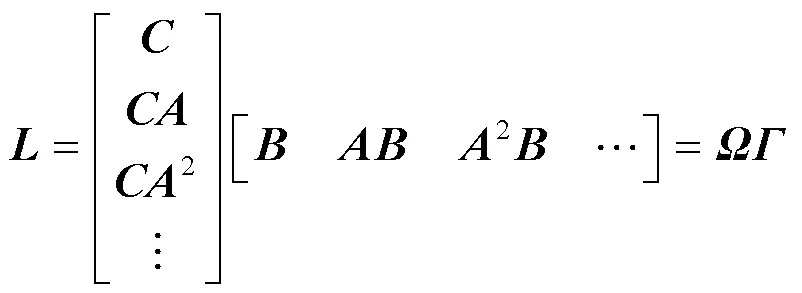
PEM算法是采用数值优化来最小化成本函数[17, 23]，即预测误差的加权范数，对于输出标量定义如式(15)所示。

考虑到采用不同时刻的采样数据得到的结果会有出入，因此通过PEM算法利用个采样数据迭代计算，缩小计算误差，得到其最佳估计值。

3 仿真分析

3.1 仿真参数设置

搭建新英格兰10机39节点仿真系统，如图4所示。

图4 10机39节点系统

算例参数设置如下：测试运行时间为100 s。系统额定频率为60 Hz，基准容量为1000 MVA，基准电压为345 kV。将所有的负荷模型均视为恒功率模型，其中G2为平衡节点。仿真系统的总容量为6192 MVA。各发电机的具体参数设置如表2所示。结合式(6)可知，此时系统的等效惯性时间常数的理论值为3.9520 s。

3.2 仿真算例

通过仿真分析4种辨识算法模型在不同扰动大小、不同采样时间窗口下的适应性。

本文使用归一化均方根误差[26-27]来衡量模型估计的输出数据与去噪后实际采样数据的拟合程度，其定义如式(17)所示。

表2 发电机参数设置

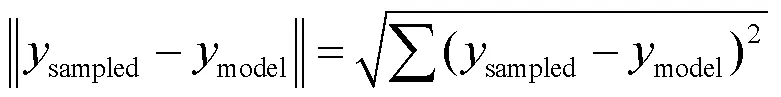
此外，通过将惯性时间常数测量结果与设定值进行比较，可得到测量误差，其定义式为

3.2.1不同扰动大小的影响

以同步机G10为例，4种系统辨识算法模型下的电力系统等效惯量响应模型的拟合度如图5所示。分析图5可知，基于PEM的SSEST模型能体现出较高的模型整体拟合度，即该模型对调频动态响应过程的整体描述能力较好。由局部放大图可知，在扰动发生的初始时刻，该辨识模型也能体现出对惯量响应初始阶段的拟合效果。此外，虽然TFEST模型也具有较高的整体拟合效果，但其对惯量响应初始阶段的拟合效果较差。

图5 惯量响应模型拟合结果(G10)

由式(20)可得表3，即场景I的测量结果。

表3 场景I的测量结果

通过对比表3中测量值可知，4种方法的测量误差均在10%以内，但本文所提出的辨识模型的求解精度最高。

场景II中不同程度的小扰动下，4种系统辨识算法模型所得的等效惯性时间常数误差如图6所示。

图6 小扰动下测量结果误差

分析可知，在负荷波动为10 MW(占比约0.0 16%)时，ARMAX模型开始出现明显的波动，在负荷波动为5 MW(占比约0.008%)时，TFEST模型开始出现明显的波动。可见TFEST模型和ARMAX模型不适用于扰动过小时，结果会出现较大波动。而N4SID模型和基于PEM的SSEST模型在系统受到极小扰动时，仍能对辨识结果进行较为准确的测量。此外，在满足测量条件下，基于PEM的SSEST模型的测量误差和波动程度均为最小，基本保持在5%以内，其结果的可靠性更高。

场景III中不同程度扰动波动下4种方法所得结果误差如图7所示。分析可知，在不同等级的大扰动情况下，4种辨识算法模型的测量结果误差均在9%以内，均能提供较为可靠的测量结果。但整体而言，ARMAX辨识模型的结果误差和波动程度更大，TFEST辨识模型的误差波动小但误差值较大。而本文所提方法具有更小测量误差值和误差波动程度。由此可得，基于PEM的SSEST算法的适用性范围较其余3种算法而言更为广泛，且所得结果具有更高的可靠性。

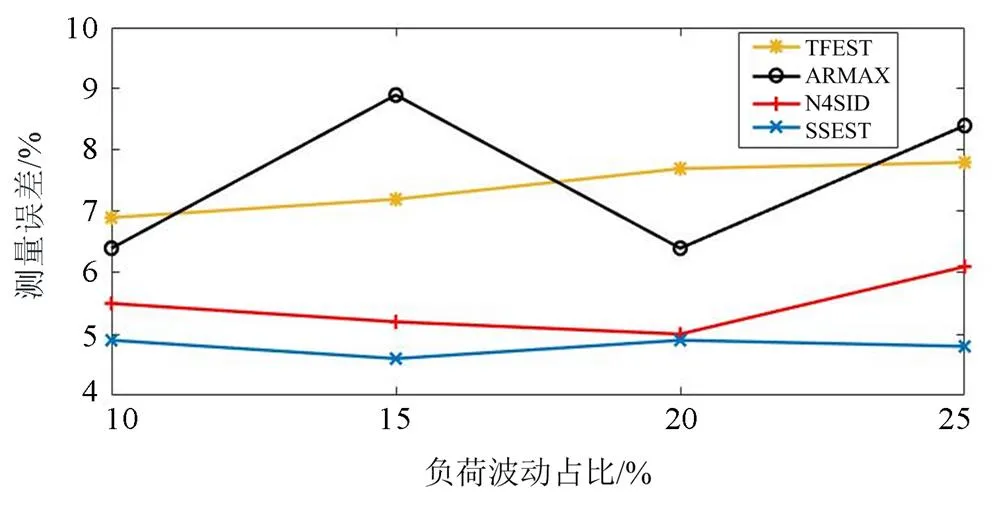
图7 不同等级扰动下测量结果误差

3.2.2不同采样窗口长度的影响

在场景I的基础上，调整不同采样时间窗口长度，通过量化分析窗口长度可探究4种系统辨识算法对惯量响应阶段辨识模型精度的影响，其误差如图8所示。

图8 不同时间窗口长度下测量结果误差

对比可知，随着采样时间窗口长度增加，除TFEST模型外，系统等效惯性时间常数计算误差出现先下降再上升的趋势。可能是因为在扰动后20 s内包含惯量响应阶段的时间长度，而随着时间的增加，结果中含着前一扰动的频率响应阶段和下一扰动的惯量响应阶段，造成误差叠加。但在5个时间段中，基于PEM的SSEST模型的测量误差均在6%以内，且波动程度较小，是4种模型中结果最优的。

综上对扰动与采样窗口的仿真分析，可以看出：本文的模型在频率小扰动事件中能保持高的数据匹配度，且在处理较小扰动和不同长度采样窗口时仍具有更优的辨识结果精度。

4 结语

本文在分析比较目前电力系统惯量测量中所用的3种系统辨识模型的基础上，提出采用基于PEM算法的SSEST模型。本文方法考虑了频率扰动程度和采样窗口长度的差异，可为在线测量电力系统等效惯量建立最优拟合模型和快速准确得到惯量测量结果提供参考。

(1) 电力系统中含有复杂的调频环节，因此在辨识模型的选择中，为保证结果的准确性，需优先考虑在惯量响应初期阶段的数据拟合程度。

(2) 与现有3种模型相比，本文所提的模型能匹配较小频率扰动事件下的数据，并得到准确的系统等效惯性时间常数。

时间窗口长度不同时，其中含有的调频阶段会对结果产生影响，而本文所提模型可准确辨识惯量响应模型，并获得系统等效惯性时间常数。

[1] 孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192.

SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192.

[2] 王凡, 李海峰, 胥国毅, 等. 调频关键参数对电网频率特性的影响及其灵敏度分析[J]. 电力系统保护与控制, 2020, 48(20): 1-8.

WANG Fan, LI Haifeng, XU Guoyi, et al. Influence of key parameters of frequency control on frequency characteristics of power grid and sensitivity analysis[J]. Power System Protection and Control, 2020, 48(20): 1-8.

[3] 蔡葆锐, 杨蕾, 黄伟. 基于惯性/下垂控制的变速型风电机组频率协调控制方法[J]. 电力系统保护与控制, 2021, 49(15): 169-177.

CAI Baorui, YANG Lei, HUANG Wei. Frequency coordination control of a variable speed wind turbine based on inertia/droop control[J]. Power System Protection and Control, 2021, 49(15): 169-177.

[4] 刘中建, 周明, 李昭辉, 等. 高比例新能源电力系统的惯量控制技术与惯量需求评估综述[J]. 电力自动化设备, 2021, 41(12): 1-11, 53.

LIU Zhongjian, ZHOU Ming, LI Zhaohui, et al. Review of inertia control technology and requirement evaluation in renewable-dominant power system[J]. Electric Power Automation Equipment, 2021, 41(12): 1-11, 53.

[5] 杨蕾, 王智超, 周鑫, 等. 大规模双馈风电机组并网频率稳定控制策略[J]. 中国电力, 2021, 54(5): 186-194.

YANG Lei, WANG Zhichao, ZHOU Xin, et al. Frequency stability control strategy for large-scale grid connections with DFIG units[J]. Electric Power, 2021, 54(5): 186-194.

[6] 杨丘帆, 王琛淇, 魏俊红, 等. 提升电网惯性与一次调频性能的储能容量配置方法[J]. 电力建设, 2020, 41(10): 116-124.

YANG Qiufan, WANG Chenqi, WEI Junhong, et al. Capacity allocation of energy storage system for improving grid inertia and primary frequency regulation[J]. Electric Power Construction, 2020, 41(10): 116-124.

[7] 江涵, 岳程燕, 严兴煜, 等. 高比例可再生能源系统惯量约束对灵活性分析的影响研究[J]. 电力系统保护与控制, 2021, 49(18): 44-51.

JIANG Han, YUE Chengyan, YAN Xingyu, et al. Influence of system inertia on flexibility resource analysis for an interconnection system with a high proportion of intermittent renewable energy[J]. Power System Protection and Control, 2021, 49(18): 44-51.

[8] YAN Cheng, TANG Yi, DAI Jianfeng, et al. Uncertainty modeling of wind power frequency regulation potential considering distributed characteristics of forecast errors[J]. Protection and Control of Modern Power Systems, 2021, 6(3): 276-288.

[9] MAGDY G, BAKEER A, ALHASHEEM M. Superconducting energy storage technology-based synthetic inertia system control to enhance frequency dynamic performance in microgrids with high renewable penetration[J]. Protection and Control of Modern Power Systems, 2022, 7(4): 460-472.

[10] 马磊, 刘国荣, 毛云坤, 等. 基于VSG的永磁直驱风电机组惯量支撑控制策略[J]. 电网与清洁能源, 2020, 36(12): 115-120.

MA Lei, LIU Guorong, MAO Yunkun, et al. Inertia support control strategy for permanent magnet direct-drive wind turbines based on VSG[J]. Power System and Clean Energy, 2020, 36(12): 115-120.

[11] ASHTON P M, SAUNDERS C S, TAYOR G A, et al. Inertia estimation of the GB power system using synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2015, 30(2): 701-709.

[12] SAGER V, JAIN S K. Estimation of power system inertia using system identification[C] // 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), May 21-24, 2019, Chengdu, China: 285-290.

[13] MAKOLO P, ZAMORA R, LIE T T. Heuristic inertia estimation technique for power networks with high penetration of RES[C] // 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), September 15-18, 2020, Bangkok, Thailand: 356-361.

[14] LUGNANI L, DANIEL D, CHRISTOPH L, et al. ARMAX-based method for inertial constant estimation of generation units using synchrophasors[J]. Electric Power Systems Research, 2020, 180.

[15] ZENG Fanhong, ZHANG Junbo, CHEN G, et al. Online estimation of power system inertia constant under normal operating conditions[J]. IEEE Access, 2020, 8: 101426-101436.

[16] BARUZZI V, LODI M, OLIVERI A, et al. Analysis and improvement of an algorithm for the online inertia estimation in pow1er grids with RES[C] // 2021 IEEE International Symposium on Circuits and Systems (ISCAS), May 22-28, 2021, Daegu, Korea: 1-5.

[17] 李言俊. 系统辨识理论及应用[M]. 北京: 国防工业出版社, 2003.

[18] LJUNG L. System identification: theory for the user[M]. Second Edition. Prentice Hall PTR, 1999.

[19] ZHANG Junbo, XU Hanchen. Online identification of power system equivalent inertia constant[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8098-8107.

[20] PINHEIRO B, LUGNANI L, DOTTA D. A procedure for the estimation of frequency response using a data-driven method[C] // 2021 IEEE Power & Energy Society General Meeting (PESGM), July 26-29, 2021, Washington, DC, USA: 1-5 .

[21] 徐波, 章林炜, 俞向栋, 等. 基于系统辨识的电力系统惯量在线评估改进方法[J]. 电力系统保护与控制, 2021, 49(18): 62-69.

XU Bo, ZHANG Linwei, YU Xiangdong, et al. An improved method of power system inertia online estimation based on system identification[J]. Power System Protection and Control, 2021, 49(18): 62-69.

[22] 李浩然, 夏智雄, 李世春. 基于子空间法的电网暂态频率扰动惯量估计[J]. 电力建设, 2021, 42(2): 2-8.

LI Haoran, XIA Zhixiong, LI Shichun. Power system inertia estimation based on subspace method under transient frequency disturbance[J]. Electric Power Construction, 2021, 42(2): 2-8.

[23] SMITH J R, FATEHI F, WOODS C S, et al. Transfer function identification in power system applications[J]. IEEE Transactions on Power Systems, 1993, 8(3): 1282-1290.

[24] 戚军, 江全元, 曹一家, 等. 电力系统传递函数的通用Prony辨识算法[J]. 中国电机工程学报, 2008, 28(28): 41-46.

QI Jun, JIANG Quanyuan, CAO Yijia, et al. A general Prony identification algorithm for power system transfer function[J]. Proceedings of the CSEE, 2008, 28(28): 41-46.

[25] ZHOU Ning, PIERRE J, HAUER J. Initial results in power system identification from injected probing signals using a subspace method[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1296-1302.

[26] 李世春, 夏智雄, 程绪长, 等. 基于类噪声扰动的电网惯量常态化连续估计方法[J]. 中国电机工程学报, 2020, 40(14): 4430-4439.

LI Shichun, XIA Zhixiong, CHENG Xuchang, et al. Continuous estimation method of power system inertia based on ambient disturbance[J]. Proceedings of the CSEE, 2020, 40(14): 4430-4439.

[27] TAMRAKER U, GURUWACHARV N, BHUJEL N, et al. Inertia estimation in power systems using energy storage and system identification techniques[C] // 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), June 24-26, 2020, Sorrento, Italy: 577-582.

Power system inertia identification based on a state space model and a PEM iterative algorithm

XU Bo1, YANG Yixin1, YU Wanqiang2, CHEN Yunan3, LI Dongdong1

(1. School of Electric Power Engineering, Shanghai University of Electric Power, Shanghai 200090, China;2. Neijiang Power Supply Company, State Grid Sichuan Electric Power Company, Neijiang 641400, China; 3. School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

Inertia is one of the important parameters which can ensure that a power system frequency is in a stable state. So it needs to be measured accurately online. Aiming at the low measurement accuracy of the current system identification method, the influence of the algorithm model in system identification on the measurement result is studied. First, the principles of inertia identification based on transfer function model, auto-regressive moving average model and subspace identification model are analyzed and compared. Secondly, a state space estimation model based on a PEM iterative algorithm is proposed from the perspective of data matching at the initial stage of the inertia response. Finally, a 10-machine and 39-bus power simulation system is built to verify the correctness of the proposed identification model. The applicability of the four identification models is analyzed under different power disturbance degrees and sampling time windows. It provides a reference for power system operators to determine the optimal identification model.

power system inertia; system identification; online measurement; iterative algorithm

10.19783/j.cnki.pspc.211432

2021-10-25；

2021-11-22

徐 波(1981—)，男，通信作者，博士，讲师，研究方向为新能源并网分析与控制等。E-mail: xubo@shiep.edu.cn

This work is supported by the National Natural Science Foundation of China (No. 51977128).

国家自然科学基金项目资助(51977128)

(编辑 魏小丽)