基于阻抗法的并网逆变器小信号稳定功率极限分析与提高

王金龙，赵浩然，王 鹏，罗 嘉，孙开宁

基于阻抗法的并网逆变器小信号稳定功率极限分析与提高

王金龙1，赵浩然1，王 鹏1，罗 嘉1，孙开宁2

(1.山东大学电气工程学院，山东 济南 2 50061；2.国网新疆电力有限公司，新疆 乌鲁木齐 830063)

随着可再生能源发电在电网中所占比重不断增加，由并网逆变器引发的电力系统小信号稳定性问题日益凸显。为了明确并网逆变器系统运行的功率裕量，增强系统的小信号稳定性，采用阻抗法对并网逆变器的小信号稳定功率极限进行研究。根据广义奈奎斯特稳定判据的边界条件定量计算了并网逆变器的小信号稳定功率极限。结果表明，该功率极限小于静态稳定功率极限，随着电网短路比的减小而减小，随着锁相环带宽的增大而减小。提出了一种改进锁相环结构，从控制的角度等效增大电网短路比，从而提高并网逆变器的小信号稳定功率极限。最后，通过阻抗分析和系统仿真验证了改进锁相环对于提高小信号稳定功率极限的有效性。

并网逆变器；小信号稳定功率极限；阻抗法；改进锁相环

0 引言

在我国“碳达峰、碳中和”的目标背景下，传统的火力发电大量地被以光伏和风电为代表的可再生能源发电所替代[1-3]。可再生能源并网促进了电力系统的大规模电力电子化[4-5]，使系统逐步呈现出“高比例可再生能源”和“高比例电力电子设备”的“双高”态势[6]。由并网逆变器所引发的新型宽频振荡问题在可再生能源渗透率高的地区频频发生，严重危害了电力系统稳定运行，限制了并网逆变器功率传输[7-8]。

并网逆变器系统的功率传输受到交流系统强度和交流系统阻抗特性的影响[9]。文献[10]从并网逆变器的角度研究了单机无穷大系统的静态稳定功率极限。文献[11]给出了并网逆变器系统的功率极限与电网短路比(Short-circuit Ratio, SCR)和逆变器功率因数的关系。然而，上述功率极限均是通过经典静态功角电压稳定性分析得到的，为理论功率极限[12]。当考虑并网逆变器系统的小信号稳定性问题时，其功率极限将不同于该理论功率极限。

分析并网逆变器系统小信号稳定性的方法主要有状态空间法[13-14]和阻抗法[15]。状态空间法通过建立整个系统的状态空间方程并求解特征值进行稳定性分析[16]。该方法需要知道并网系统的详细结构和全部参数，而在实际中由于行业保密性要求，系统的一些参数和结构往往是不可知的，这降低了采用状态空间法进行稳定性分析的可行性。并且对于高维并网系统还会出现维数灾的问题[17]。阻抗法将并网系统分为逆变器子系统和电网子系统分别建立阻抗模型，再基于奈奎斯特判据分析系统稳定性。如果系统的一部分发生变化，只有变化所在的子系统受到影响，而不需要对整个系统重新进行建模，降低了系统分析的难度[18]。而且即使不知道系统的详细结构和参数，也可以通过实验测量辨识其阻抗模型[19-20]。因此，阻抗法已经成为研究并网逆变器系统小信号稳定性的重要方法之一。

文献[12]采用状态空间法分析了并网逆变器控制对其功率传输的影响，指出锁相环参数对并网逆变器小信号稳定功率极限有较大影响。文献[21]采用阻抗法研究了并网逆变器控制回路间的相互作用对功率稳定极限的影响机理，但没有定量给出功率极限。文献[22]基于频率耦合阻抗模型对变流器系统进行全工况小信号稳定性分析，给出了系统在不同电网阻抗下的稳定功率极限。然而，文中采用逐点分析的方法，计算量较大。为了提高并网逆变器的小信号稳定功率极限，可以从增强系统稳定性的角度出发。文献[23-24]对锁相环控制参数进行调节，以减小锁相环带宽。优化控制参数的方法应用简单，但效果有限，同时也会对控制器动态性能产生影响。除此之外，还可以采用优化控制结构的方法。文献[25]采用多PR控制结构塑造并网逆变器阻抗，减少逆变器与弱电网之间的谐波扰动，提高系统功率传输能力。文献[26]则通过虚拟阻抗前馈并网点电压对逆变器阻抗进行串并联校正，从而提高系统运行的稳定性。

为了定量给出并网逆变器的小信号稳定功率极限，本文基于并网逆变器坐标系阻抗模型，通过广义奈奎斯特稳定判据(Generalized Nyquist Stability Criterion, GNC)的边界条件对其进行计算。并且分析了电网短路比和锁相环带宽对并网逆变器小信号稳定功率极限的影响。最后提出了一种改进锁相环结构以提高并网逆变器的小信号稳定功率极限，并通过阻抗分析和系统仿真进行了验证。

1 并网逆变器系统阻抗模型

1.1 并网逆变器系统结构

并网逆变器的系统结构如图1所示，包含主电路和控制器两部分。其中：g为电网电压；g和g分别为电网等效电感和电阻；s和s分别为并网点(Point of Common Coupling, PCC)电压和电流；f和f分别为逆变器滤波电感和电阻；c为逆变器输出电压。控制策略采用电压定向矢量控制(Voltage-oriented Control, VOC)。假设直流端电压dc恒定，只考虑电流内环控制。同步参考坐标系锁相环(Synchronous Reference Frame Phase-Locked Loop, SRF-PLL)产生参考角度用于与电网电压保持同步。附表1给出了并网逆变器系统的主要参数。

图1 并网逆变器系统结构图

1.2 并网逆变器dq坐标系下阻抗模型

采用VOC控制的并网逆变器在坐标系下实现电流控制，与线性化方法的基本思想相符。因此，采用线性化的方法推导并网逆变器坐标系阻抗模型[27-28]。

图2表示了并网逆变器各部分小信号阻抗模型之间的关系。根据该模型框图，可以得到并网逆变器的坐标系下的阻抗模型为

式中：I为单位对角矩阵。、、、详见附录B。

采用坐标系阻抗测量方法[29]对推导得到的阻抗表达式(1)进行验证。电网阻抗为0.5W三相电阻，其余参数选取参考附表1。电流参考值的给定使并网逆变器输出额定功率。单位功率因数的情况下，-通道和-通道的阻抗幅值很小，因测量方法精度有限，在仿真测量中可以忽略。推导得到的阻抗模型与仿真测量的结果对比如图3所示，验证了阻抗模型的正确性。

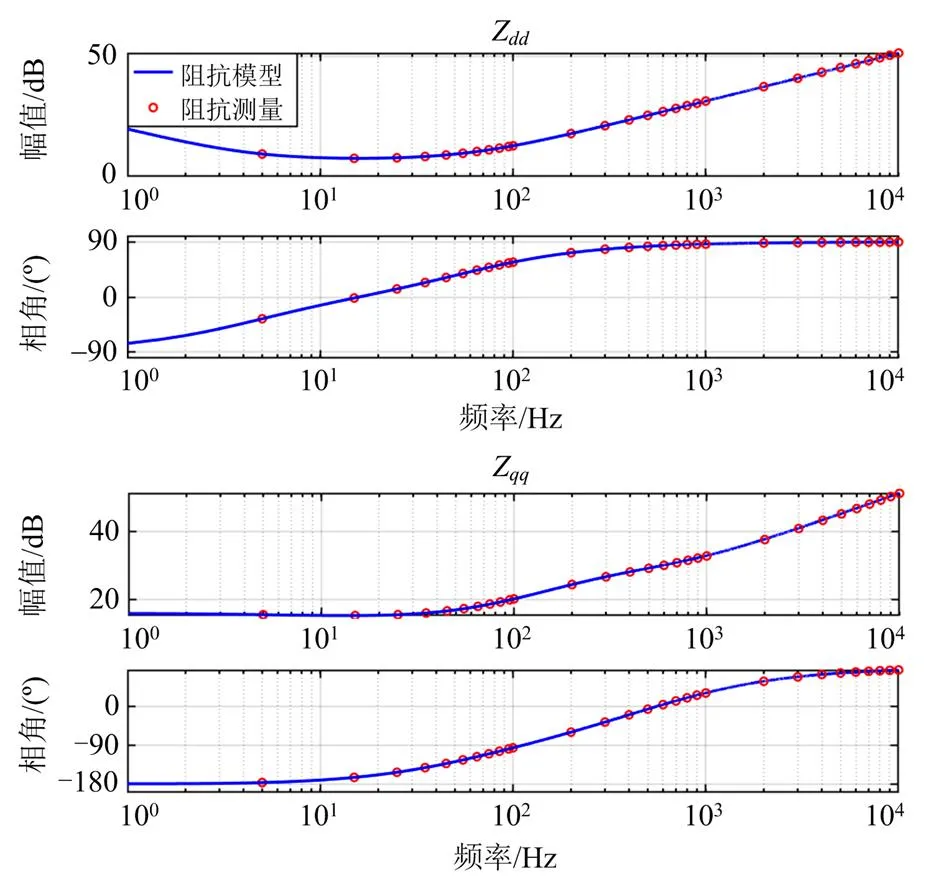
图3 并网逆变器阻抗模型与仿真测量对比

1.3 电网侧dq坐标系下阻抗模型

电网侧电路在坐标系下的数学模型为

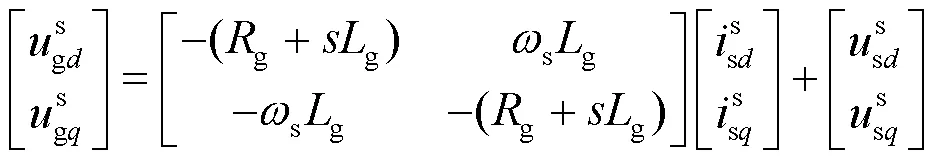
将式(2)进行小信号线性化，得到式(3)。

2 并网逆变器小信号稳定功率极限

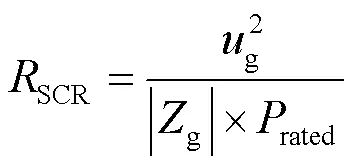
然而，在实际运行中，并网逆变器的功率传输能力还受到控制策略及控制参数的影响，并不能达到式(5)所给出的理论最大功率。当逆变器输出功率增大到一定数值时，并网系统会出现小信号失稳现象。因此，本节根据广义奈奎斯特稳定判据计算并网逆变器的小信号稳定功率极限，并分析电网短路比和锁相环带宽对其的影响。

2.1 小信号稳定功率极限计算

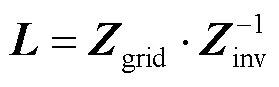
1) 假设并网逆变器小信号稳定功率极限为s，通过潮流计算确定系统稳态运行点，并表示为s的函数。

逆变器输出功率与并网点电压电流的关系为

联合式(2)和式(B1)，并且稳态时微分项为0，可以求解出以有功功率表示的并网逆变器系统电压和电流的稳态值。

3) 根据系统小信号临界稳定状态判别条件构造小信号稳定功率极限方程，形式为

4) 在系统参数已知的条件下，上述方程为关于s和的非线性代数方程组，采用牛顿法进行求解，得到两组数值解，选择较小的功率值作为当前并网逆变器系统条件下的小信号稳定功率极限。

5) 根据所求小信号稳定功率极限采用广义奈奎斯特稳定判据进行验证。

图4 小信号稳定功率极限算法流程图

图5 输出功率为23 kW时广义奈奎斯特图

保持当前系统参数不变，不断增大输出功率，然后采用广义奈奎斯特稳定判据进行稳定性判断。随着输出功率的增大，阻抗比值的特征轨迹逐渐接近(-1, 0)点，并最终包围这一点，系统由稳定状态过渡到不稳定状态。在输出功率为24.15 kW时，特征轨迹正好穿过(-1, 0)点，系统处于临界稳定状态，如图6所示。根据输出功率增大时并网逆变器系统阻抗比的广义奈奎斯特图变化情况，验证了并网逆变器小信号稳定功率极限算法的正确性。

图6 输出功率为24.15 kW时的广义奈奎斯特图

2.2 小信号稳定功率极限影响因素

在附表1所示参数下，保持电网阻抗角以及逆变器单位功率因数和控制参数不变，改变电网阻抗的幅值，从而改变电网短路比。计算相应电网短路比下的并网逆变器小信号稳定功率极限，并与理论功率极限进行比较，如图7所示。其中，蓝色曲线表示并网逆变器小信号稳定功率极限与电网短路比的关系。可以看出，并网逆变器的小信号稳定功率极限小于相应条件下的理论功率极限，并且随着短路比的降低，并网逆变器的功率传输能力逐渐下降。

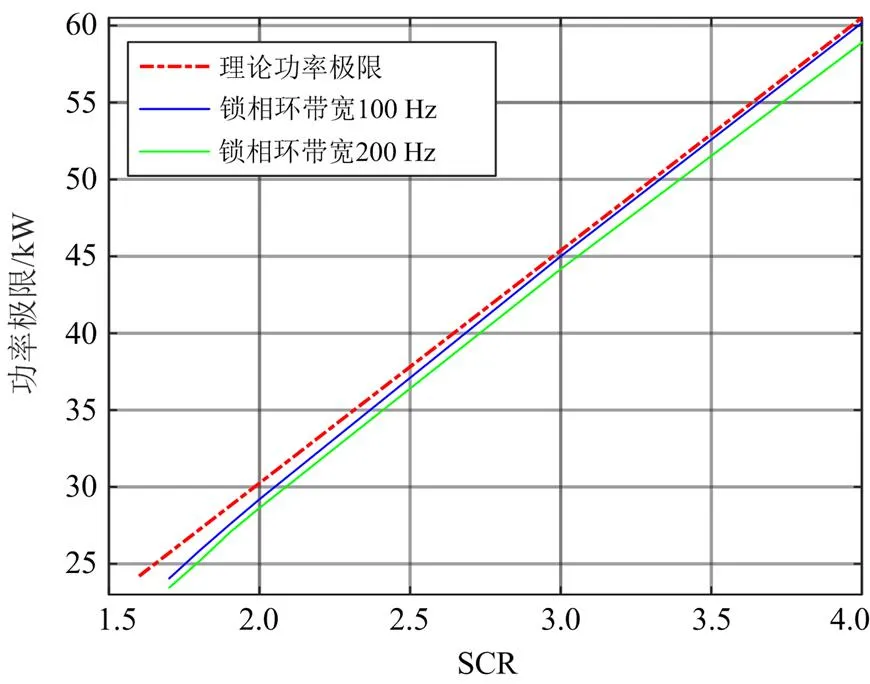
图7 小信号稳定功率极限与SCR和SRF-PLL的关系

改变SRF-PLL的PI参数，研究锁相环带宽对并网逆变器小信号稳定功率极限的影响。图7中绿色曲线表示SRF-PLL带宽增大到200 Hz时，并网逆变器的小信号稳定功率极限随SCR变化的关系。可以看出，随着锁相环带宽的增大，并网逆变器功率传输能力减弱。这与文献[31]中的随着锁相环带宽的增加，逆变器输出阻抗的负电阻频率范围增加，从而导致系统更易失稳的结论相符。

3 改进锁相环

3.1 改进锁相环原理

由上述分析可知，采用较小的锁相环带宽和较大的电网短路比可以提高并网逆变器的小信号稳定功率极限，使其更加逼近理论功率极限。然而，锁相环带宽过小会影响其对并网电压相角的跟踪功能，使系统动态性能变差。同时，系统一定时，电网阻抗以及逆变器额定功率都是一定的，实际的电网短路比不能随意改变。因此，本文提出了一种改进锁相环结构，如图8所示。从控制的角度等效增大电网短路比，从而提高并网逆变器在实际并网点处的小信号稳定功率极限。将并网点的电流也引进锁相环中，通过一个与电网阻抗成比例的虚拟阻抗与并网点电压进行相加，然后进行锁相。由图8可知

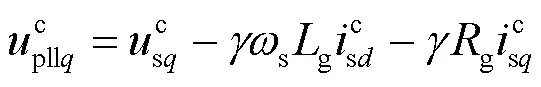
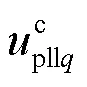
图8 改进锁相环结构图

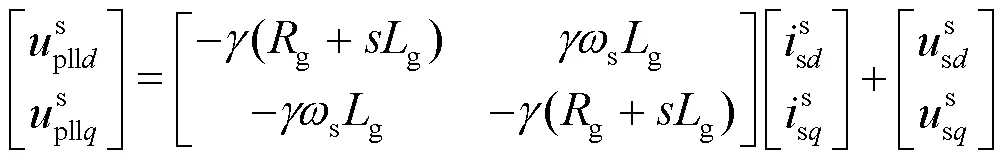
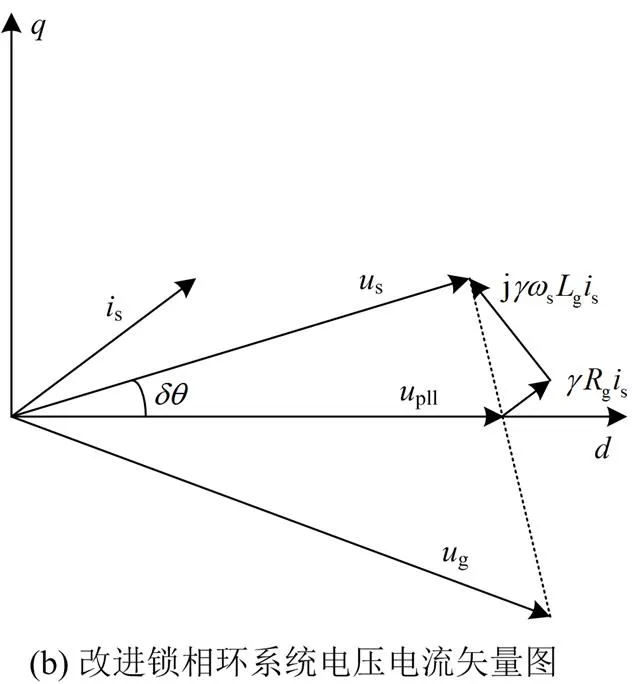
图9 改进锁相环锁相电压

由上述分析可知，改进锁相环相当于将并网点人为改变了，使其更加靠近电网那一侧，等效于减小了电网阻抗。根据式(4)可知，电网阻抗减小，电网短路比增大，从而使得并网逆变器在实际并网点处所能传输的最大功率增加。同时，因为系统坐标系定向的改变，改进锁相环并网逆变器和传统锁相环并网逆变器在实际并网点输出相同功率时，电流参考值的取值不同。

3.2 改进锁相环并网逆变器阻抗模型

本节推导采用改进锁相环的并网逆变器坐标系阻抗模型并对其阻抗特性进行分析。与采用传统锁相环的并网逆变器的结构相比，只有锁相环部分发生了变化，其余部分不变，因此只需要重新推导改进锁相环的坐标系下阻抗模型。

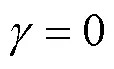
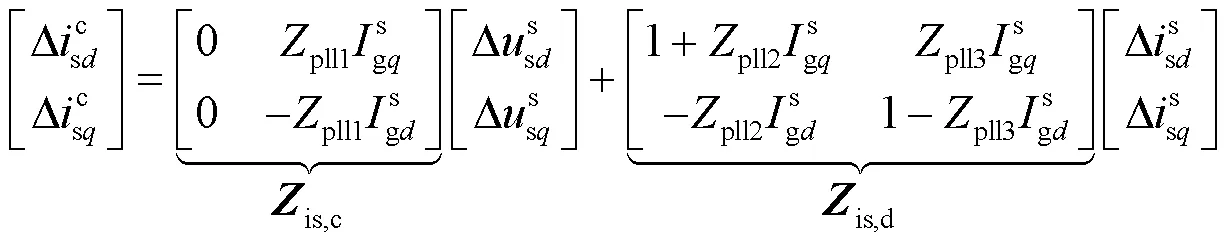
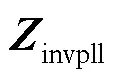
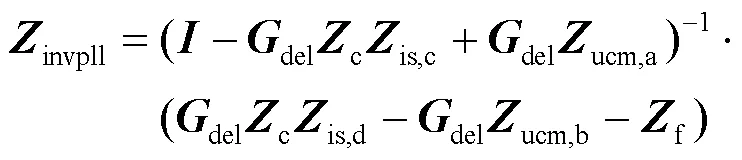
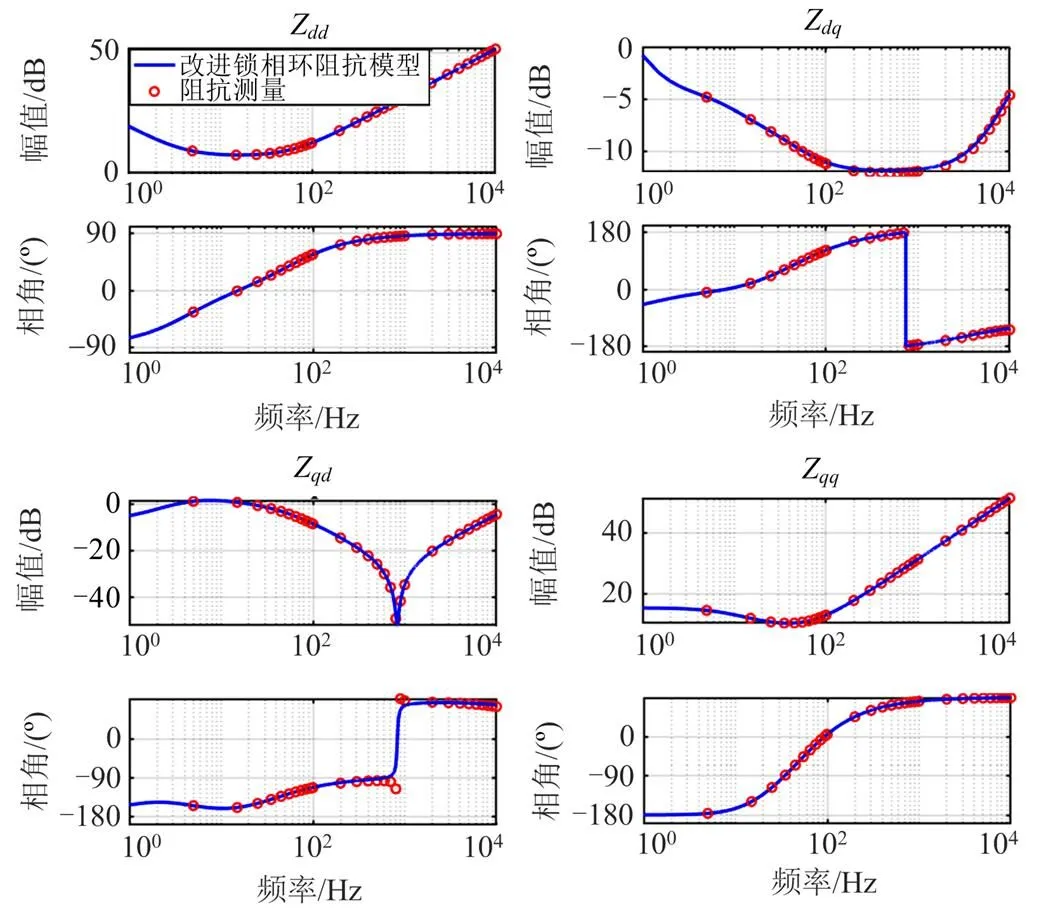
图11 改进锁相环并网逆变器阻抗模型与仿真测量对比

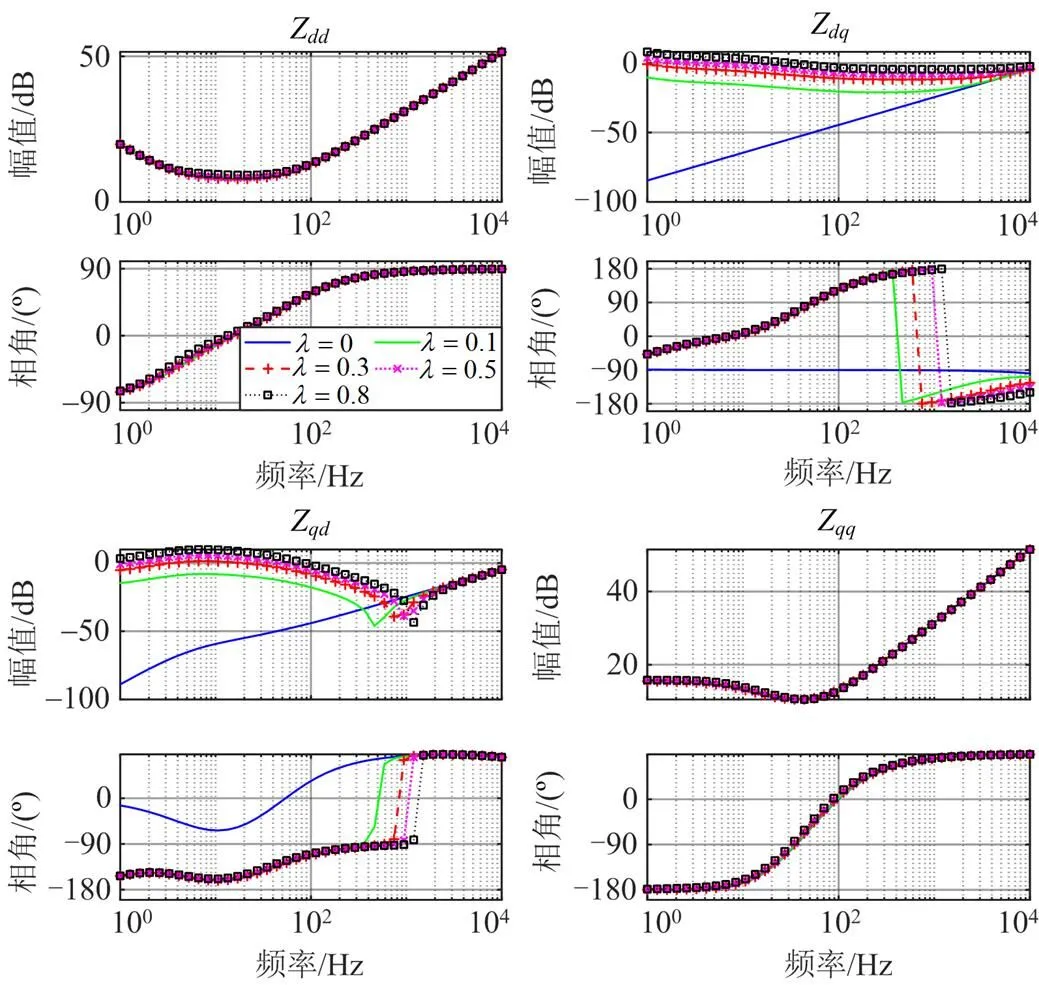
图12 改进锁相环并网逆变器阻抗特性

3.3 改进锁相环并网逆变器功率极限

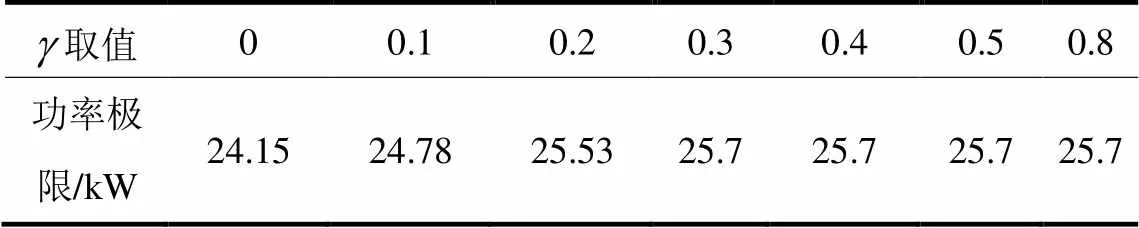
表1 不同 g 取值时的小信号稳定功率极限

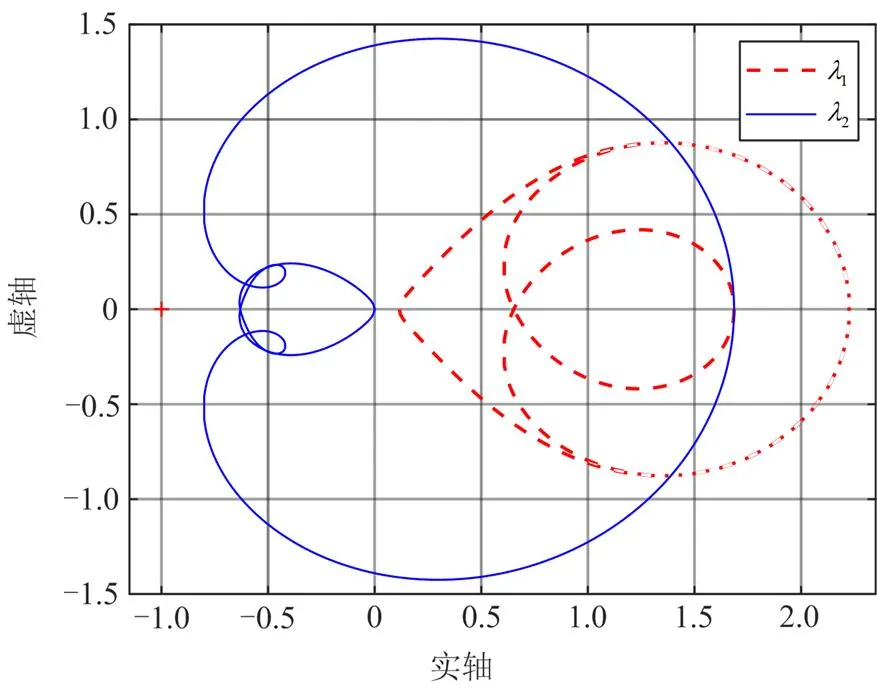
图13 输出功率为25.7 kW时的广义奈奎斯特图

保持电网阻抗角以及逆变器功率因数和控制参数不变，改变电网阻抗的幅值。然后计算相应电网短路比下的功率极限，得到改进锁相环并网逆变器的小信号稳定功率极限与电网短路比的关系，并与理论功率极限和采用传统锁相环的小信号稳定功率极限进行比较，结果如图14所示。可以看出，采用改进锁相环之后，并网逆变器的小信号稳定功率极限得到提高，基本可以达到理论功率传输极限。

4 仿真验证

根据图1所示并网逆变器系统结构以及图8所示改进锁相环结构，在Matlab/Simulink中搭建仿真模型，系统参数设置与附表1相同。通过仿真验证了并网逆变器小信号稳定功率极限算法的正确性以及改进锁相环的有效性。

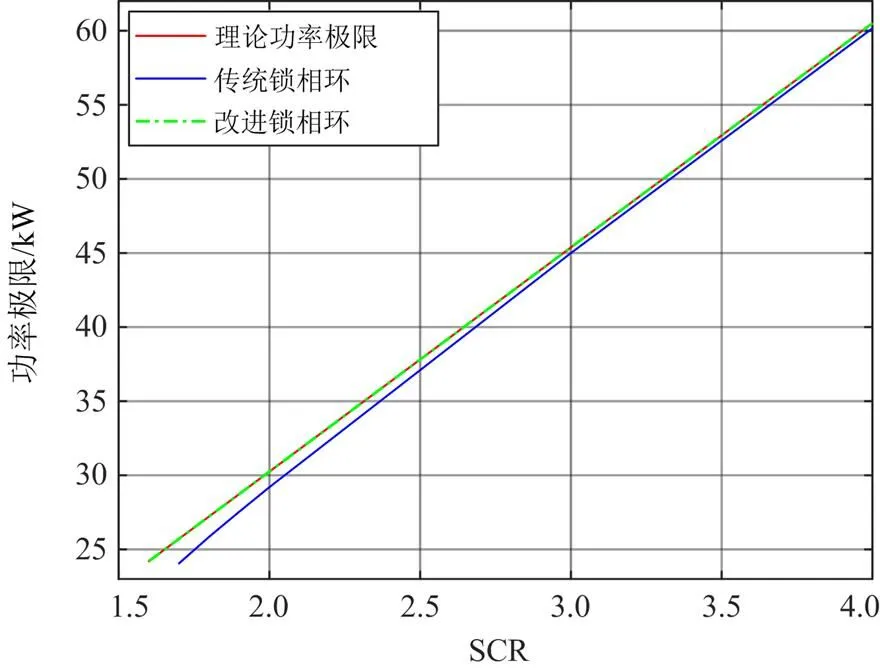
图14 改进锁相环并网逆变器小信号稳定功率极限

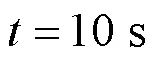
图15 PCC电压和输出功率仿真波形

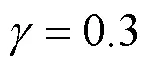
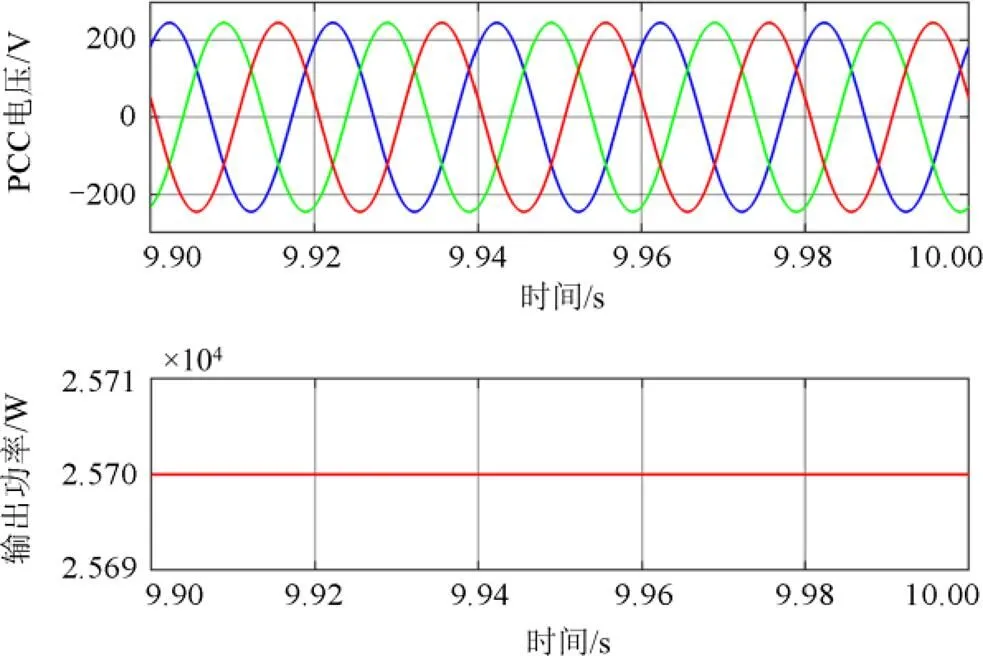
图16 改进锁相环并网逆变器仿真波形

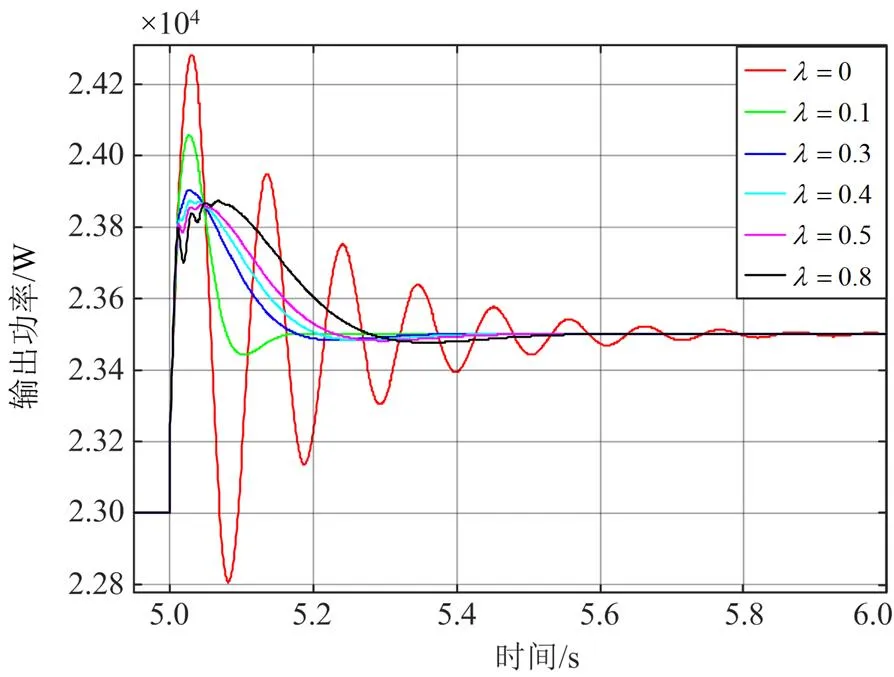
图17 输出功率变化时不同 g 取值的系统动态响应

5 结论

本文从系统小信号稳定的角度，分析并网逆变器的功率传输极限，提出了一种改进锁相环结构以提高并网逆变器的功率传输能力，并通过系统仿真进行验证。主要结论如下：

1) 并网逆变器的小信号稳定功率极限小于同等条件下的理论功率极限，并且随着电网短路比的减小而减小，随着锁相环带宽的增大而减小。

2) 提出的改进锁相环结构实现简单，只需在现有的锁相环结构中进行修改，且不需要改变锁相环原有控制参数，同时具有较好的稳态性能和动态性能，具有一定的实际工程应用价值。

3) 改进锁相环结构可以显著提高并网逆变器在实际运行点处的小信号稳定功率极限，通过选择合适的参数，基本可以达到理论功率传输极限，提高了系统运行稳定性和并网逆变器功率传输效率。

附表1 并网逆变器系统参数

Attached Table 1 Parameters of grid-connected inverter system

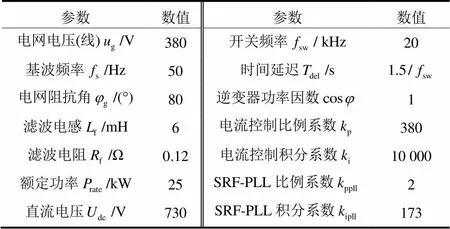
参数数值参数数值 电网电压(线)/V380开关频率/ kHz20 基波频率/Hz50时间延迟/s 电网阻抗角/(°)80逆变器功率因数1 滤波电感/mH6电流控制比例系数380 滤波电阻/Ω0.12电流控制积分系数10 000 额定功率/kW25SRF-PLL比例系数2 直流电压/V730SRF-PLL积分系数173

逆变器的滤波电路在电网系统坐标系下的数学模型为

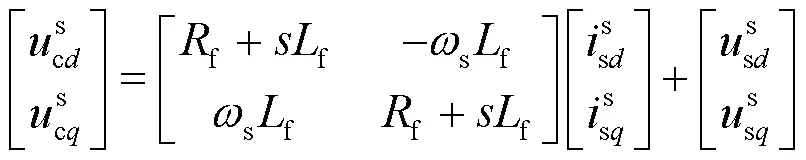
式中：为拉格朗日乘子；s为电网基波角速度。

对式(B1)进行小信号线性化，可以得到滤波电路坐标系下的阻抗模型为

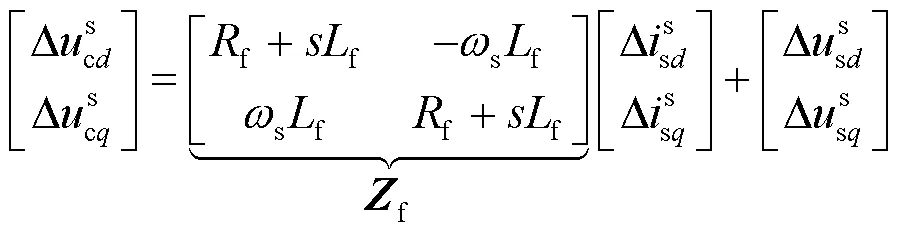
式中，符号“Δ”表示相应变量的小信号扰动量。

电流控制环在控制系统坐标系下的表达式为

考虑小信号扰动，可得电流控制环坐标系下的阻抗模型为

数字控制系统的时间延迟del用del表示。在最严重的情况下，包括一个采样周期的计算延迟和半个采样周期的PWM延迟。

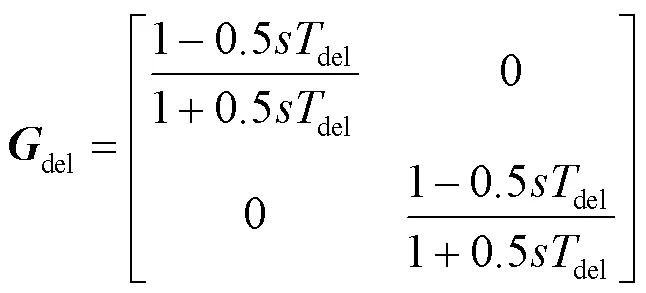
在并网逆变器系统处于稳态时，控制系统坐标系与电网系统坐标系重合。然而，当PCC电压出现小信号扰动时，由于SRF-PLL的动态特性，通过SRF-PLL获得的相角与实际PCC电压相角会存在偏差Δ，即控制系统坐标系与电网系统坐标系不再重合，存在偏差Δ。逆变器控制系统采用控制系统坐标系对电压、电流进行坐标变换，SRF-PLL的小信号扰动传递到电压、电流的轴分量中，经过控制器输出后，扰动进一步传递到电网系统中。根据文献[20]，有

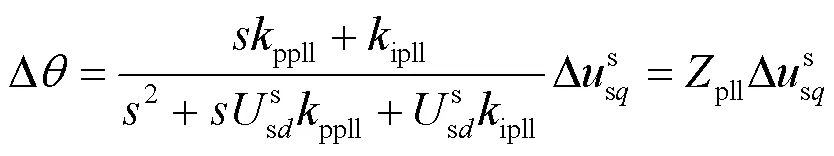
因此，电网系统坐标系下和控制系统坐标系下的电压、电流轴和轴分量有如下关系。

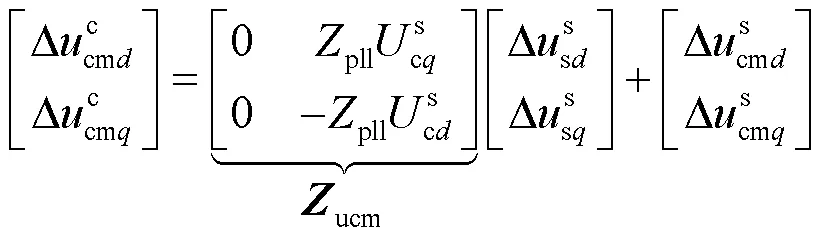
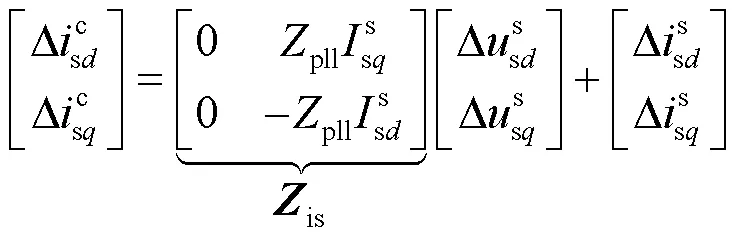
[1] 江涵, 岳程燕, 严兴煜, 等. 高比例可再生能源系统惯量约束对灵活性分析的影响研究[J]. 电力系统保护与控制, 2021, 49(18): 44-51.

JIANG Han, YUE Chengyan, YAN Xingyu, et al. Influence of system inertia on flexibility resource analysis for an interconnection system with a high proportion of intermittent renewable energy[J]. Power System Protection and Control, 2021, 49(18): 44-51.

[2] 兰洲, 蒋晨威, 谷纪亭, 等. 促进可再生能源发电消纳和碳减排的数据中心优化调度与需求响应策略[J]. 电力建设, 2022, 43(4): 1-9.

LAN Zhou, JIANG Chenwei, GU Jiting, et al. Optimal dispatch and demand response strategies of data centers for promoting accommodation of renewable energy generation and reducing carbon emission[J]. Electric Power Construction, 2022, 43(4): 1-9.

[3] 张鑫, 李媛媛, 吉平. 含高比例可再生能源的交直流混联电网规划方法[J]. 全球能源互联网, 2021, 4(4): 372-381.

ZHANG Xin, LI Yuanyuan, JI Ping. A planning approach for AC/DC hybrid power grid with high proportion of renewable energy[J]. Journal of Global Energy Interconnection, 2021, 4(4): 372-381.

[4] 胡家兵, 袁小明, 程时杰. 电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题[J]. 中国电机工程学报, 2019, 39(18): 5457-5467, 5594.

HU Jiabing, YUAN Xiaoming, CHENG Shijie. Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus[J]. Proceedings of the CSEE, 2019, 39(18): 5457-5467, 5594.

[5] 陈垣, 张波, 谢帆, 等. 电力电子化电力系统多时间尺度建模与算法相关性研究进展[J]. 电力系统自动化, 2021, 45(15): 172-183.

CHEN Yuan, ZHANG Bo, XIE Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.

[6] 马宁宁, 谢小荣, 唐健, 等. “双高”电力系统宽频振荡广域监测与预警系统[J]. 清华大学学报(自然科学版), 2021, 61(5): 457-464.

MA Ningning, XIE Xiaorong, TANG Jian, et al. Wide-area measurement and early warning system for wide-band oscillations in "double-high" power systems[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(5): 457-464.

[7] 杨博闻, 占颖, 谢小荣, 等. 双馈风电场接入串补输电系统引发次同步谐振的研究模型[J]. 电力系统保护与控制, 2020, 48(8): 120-126.

YANG Bowen, ZHAN Ying, XIE Xiaorong, et al. A study model for subsynchronous resonance in DFIG based wind farms connected to a series-compensated power system[J]. Power System Protection and Control, 2020, 48(8): 120-126.

[8] 徐衍会, 耿雨柔, 杨博文. 风电场引发火电机组次同步振荡的机理及影响因素研究[J]. 电力系统保护与控制, 2021, 49(18): 1-9.

XU Yanhui, GENG Yurou, YANG Bowen. Study on the mechanism and influencing factors of subsynchronous oscillations induced by wind farms in a fossil fuel power plant[J]. Power System Protection and Control, 2021, 49(18): 1-9.

[9] ZHOU J Z, GOLE A M. VSC transmission limitations imposed by AC system strength and AC impedance characteristics[C] // IET International Conference on AC & DC Power Transmission, December 4-5, 2012, Birmingham, UK: 1-6.

[10]康勇, 林新春, 郑云, 等. 新能源并网变换器单机无穷大系统的静态稳定极限及静态稳定工作区[J]. 中国电机工程学报, 2020, 40(14): 4506-4515, 4730.

KANG Yong, LIN Xinchun, ZHENG Yun, et al. The static stable-limit and static stable-working zone for single-machine infinite-bus system of renewable-energy grid-connected converter[J]. Proceedings of the CSEE, 2020, 40(14): 4506-4515, 4730.

[11] YANG D, WANG X, LIU F, et al. Adaptive reactive power control of PV power plants for improved power transfer capability under ultra-weak grid conditions[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1269-1279.

[12] ZHOU J Z, DING H, FAN S, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.

[13] KREIN P T, BENTSMAN J, BASS R. M, et al. On the use of averaging for the analysis of power electronic systems[J]. IEEE Transactions on Power Electronics, 1990, 5(2): 182-190.

[14] 田艳军, 陈映妃, 王慧, 等. 光伏级联DC/DC变换器模式切换稳定性分析及降压运行策略[J]. 电力建设, 2020, 41(1): 97-105.

TIAN Yanjun, CHEN Yingfei, WANG Hui, et al. Mode switching stability analysis and step-down operation strategy of photovoltaic cascaded DC/DC converters[J]. Electric Power Construction, 2020, 41(1): 97-105.

[15] MIDDLEBROOK R. Input filter considerations in design and application of switching regulators[C] // IEEE Industrial Application Society Annual Meeting, October 11-14, 1976, Chicago, IL, USA: 366-382.

[16] 陈新, 王赟程, 龚春英, 等. 采用阻抗分析方法的并网逆变器稳定性研究综述[J]. 中国电机工程学报, 2018, 38(7): 2082-2094, 2223.

CHEN Xin, WANG Yuncheng, GONG Chunying, et al. Overview of stability research for grid-connected inverters based on impedance analysis method[J]. Proceedings of the CSEE, 2018, 38(7): 2082-2094, 2223.

[17] 张天翼, 王海风. 风电并入弱交流系统引发次同步振荡的研究方法综述[J]. 电力系统保护与控制, 2021, 49(16): 177-187.

ZHANG Tianyi, WANG Haifeng. Research methods for subsynchronous oscillation induced by wind power under weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187.

[18] SUN J. Small-signal methods for AC distributed power systems-a review[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2545-2554.

[19] ZHANG M, WANG X, YANG D, et al. Transfer learning for identifying impedance estimation in voltage source inverters[C] // IEEE Energy Conversion Congress and Exposition (ECCE), October 11-15, 2020, Detroit, USA: 6170-6174.

[20] GONG H, WANG X, YANG D. DQ-frame impedance measurement of three-phase converters using time-domain MIMO parametric identification[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2131-2142.

[21] HUANG Y, WANG D. Effect of control-loops interactions on power stability limits of VSC integrated to AC system[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 301-310.

[22] 刘威, 谢小荣, 王衡, 等. 基于频率耦合阻抗模型的并网变流器全工况小信号稳定性分析[J]. 中国电机工程学报, 2020, 40(22): 7217-7221.

LIU Wei, XIE Xiaorong, WANG Heng, et al. Frequency- coupled impedance model-based small-signal stability analysis of grid-tied converters under all operating conditions[J]. Proceedings of the CSEE, 2020, 40(22): 7217-7221.

[23] ARANIM F M, MOHAMED Y A R I. Analysis and performance enhancement of vector-controlled VSC in HVDC links connected to very weak grids[J]. IEEE Transactions on Power Systems, 2017, 32(1): 684-693.

[24] CESPEDE M, SUN J. Adaptive control of grid-connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.

[25] WANG F, DUARTE J L, HENDRIX M, et al. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 786-797.

[26] YANG D, RUAN X, WU H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5795-5805.

[27] WANG X, HARNEFORS L, BLAABJERG F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1775-1787.

[28] 王胜, 冯兴明, 周宇, 等. 基于BP神经网络预测的微网系统轴谐波阻抗的主动测量策略[J]. 电测与仪表, 2021, 58(3): 118-125.

WANG Sheng, FENG Xingming, ZHOU Yu, et al. An active measurement strategy of-axis harmonic impedance in micro-grid system based on BP neural network prediction[J]. Electrical Measurement & Instrumentation, 2021, 58(3): 118-125.

[29] WEN B, BOROYEVICH D, BURGOS R, et al. Small-signal stability analysis of three-phase AC systems in the presence of constant power loads based on measured d-q frame impedances[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5952-5963.

[30] MACFARLANE A G J, POSTLETHWAITE I. The generalized nyquist stability criterion and multivariable root loci[J]. International Journal of Control, 1977, 25: 81-127.

[31] WEN B, BOROYEVICH D, BURGOS R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.

Analysis and improvement of the small-signal stable power limit of a grid-connected inverter based on an impedance method

WANG Jinlong1, ZHAO Haoran1, WANG Peng1, LUO Jia1, SUN Kaining2

(1. School of Electrical Engineering, Shandong University, Jinan 250061, China;2.State Grid Xinjiang Electric Power Co., Ltd., Urumqi 830063, China)

As the proportion of renewable energy power generation in the grid continues to increase, the problem of power system small-signal stability caused by grid-connected inverters has become increasingly prominent. To clarify the power margin of the grid-connected inverter system and improve the small-signal stability of the system, the impedance method is used to study the small-signal stable power limit of the inverter. From the boundary conditions of the generalized Nyquist stability criterion, the small-signal stable power limit of the grid-connected inverter is quantitatively calculated. It is pointed out that the power limit is less than the static stability power limit, and decreases with the decrease of the grid short-circuit ratio, and decreases with the increase of the phase-locked loop bandwidth. An improved phase-locked loop structure is proposed to increase the grid short-circuit ratiofrom the control point of view, thereby improving the small-signal stable power limit of the grid-connected inverter. Finally, the effectiveness of the improved phase-locked loop in improving the small-signal stable power limit is verified by impedance analysis and system simulation.

grid-connected inverter; small-signal stable power limit; impedance method; improved phase-locked loop

10.19783/j.cnki.pspc.211570

2021-11-21；

2022-05-23

王金龙(1997—)，男，硕士研究生，研究方向为风机并网稳定性分析；E-mail: 201934314@mail.sdu.edu.cn

赵浩然(1983—)，男，通信作者，教授，博士生导师，研究方向为风力发电及并网、综合能源系统运行与控制。E-mail: hzhao@sdu.edu.cn

This work is supported by theNational Natural Science Foundation of China (No. 51707106).

国家自然科学基金项目资助(51707106)

(编辑 周金梅)