基于断线扰动的电压控制区域边界节点修正方法

娄奇鹤，王 康，袁铁江，董力通,3

基于断线扰动的电压控制区域边界节点修正方法

娄奇鹤1，王 康2，袁铁江2，董力通2,3

(1.国家电网有限公司，北京 100031；2.大连理工大学电气工程学院，辽宁 大连 116024；3.国网经济技术研究院有限公司，北京 102209)

电压控制区域(Voltage Control Area, VCA)之间具有弱耦合性，修正VCA能够提升区域内电压变化的一致性，从而优化电网分区结果。传统分区修正法存在计算量大、PV节点归并缺乏理论依据等问题。因此，提出了一种修正VCA边界节点的方法，可以有效减少分区修正的计算量。所提方法采用小元素去除法得到各阈值下的电网划分结果，以曲线为判据选取各划分结果中最佳阈值对应的准分区。基于区域间的弱耦合性，采用所提方法修正准分区，得到优化后的分区结果。所提方法针对准分区的边界节点进行断线修正，并采用平均电气距离归并剩余的PV节点，不仅能减少分区修正的计算量，而且为各区域无功源的合理分配提供了理论依据。以新英格兰10机39节点系统为算例，通过仿真分析验证了所提方法的有效性。

断线扰动；电压控制区域；阈值分析；平均电气距离；电压稳定性

0 引言

随着电力系统的升级，电网结构日趋复杂，电压稳定性问题日益突出，局部失稳有可能会影响整个电网的稳定运行[1]。采用合理的电压控制方案，将系统划分为若干个具有电压稳定特征的区域[2]，便于进行电压的就地控制，对于维持电网的稳定运行具有重要意义[3-4]。

在电力系统中，电压控制区域(Voltage Control Area, VCA)指负荷功率变化与电压响应一致的节点簇[5]。区域内各节点联系紧密，与其他区域电气联系薄弱，适合进行区域内控制[6]。当电力系统发生局部失稳时，各区域电压控制措施可以弥补区域无功短缺，因此这些节点组成的区域被称为VCA[7]，国内外学者针对VCA的划分进行了广泛研究。

在分区模型与方法方面，文献[8]研究了有功潮流灵敏度与综合灵敏度的计算方法，采用AP聚类得到了电网分区。文献[9]引入改进的Fast-Newman算法，考虑了无功/有功-电压灵敏度矩阵的改进模块度，可更为细致合理地划分配网。文献[10]提出了一种新颖的等周聚类划分法，能够得到较好的划分结果。文献[11]引入了改进的电气距离，通过谱聚类法对临界负荷母线判断并进行电网划分，提高了电压稳定性。文献[12]通过-曲线确定连接点无功裕度，进行电压稳定性评估。文献[13]通过K-means算法得到离散化电气距离矩阵，采用AP聚类法进行了电网分区，文献[14]基于主导节点的选择，加强了分区内电源对换流站的电压控制能力。针对分区结果进一步优化的方面，现有研究主要是针对随机扰动[15-16]、全网负荷支路扰动[17]引起的节点电压波动，以及潮流断面进行修正[18]，但针对受到扰动之后各区域电压薄弱环节的修正问题却鲜有研究。

根据电压控制区域的定义“区域内强耦合，区域间弱耦合”[5]可知，各分区之间电气耦合程度弱，区域的边界即为电网的电压薄弱环节。文中建立了含弱耦合关系的改进阈值划分模型，提出了一种基于VCA边界节点的修正方法。该方法以区域的边界节点为对象进行修正，并采用平均电气距离合并修正后的无功源节点，能够减少传统分区结果划分优化的计算量，同时可以合理地分配各区域的无功资源，为实现区域电压稳定控制、提高分区优化的效率提供了条件。

1  阈值分析划分方法

阈值分析法有两个过程：(1) 负荷节点曲线的极小值对比过程；(2) 阈值划分小元素去除过程。曲线可以反映系统电压变化的一致性，得到具有电压稳定特征的VCA[19]。小元素去除法能够清晰地描绘节点功率和电压的关系。因此，阈值分析法优于传统电气距离法。针对最佳阈值对应的准分区，采用边界修正法，得到修正后的VCA。

1.1 Q-V曲线

为选择合适的阈值，文献[20]提出利用相似“鼻尖点”(min,min)的曲线方法，通过连续潮流计算方法[21]得到负荷节点的曲线。利用曲线的方法能得到电压变化一致的VCA，是因为区域内部电压幅值变化具有一致性。

比较所有负荷节点的曲线，将极小值点(min,min)近似一致且在该点达到无功限值的发电机组划为一个区域，重复此过程直至完成所有节点的对比，为小元素去除法最佳阈值选择提供判据。系统统曲线的对比图如图1所示。

由图1(a)可知，虽然节点1和节点2的无功限值相同，但是其“鼻尖点”(min,min)不同，因此不能为一个区域。图1(b)中节点1、2的无功限值与(min,min)基本一致，可划为同一VCA。

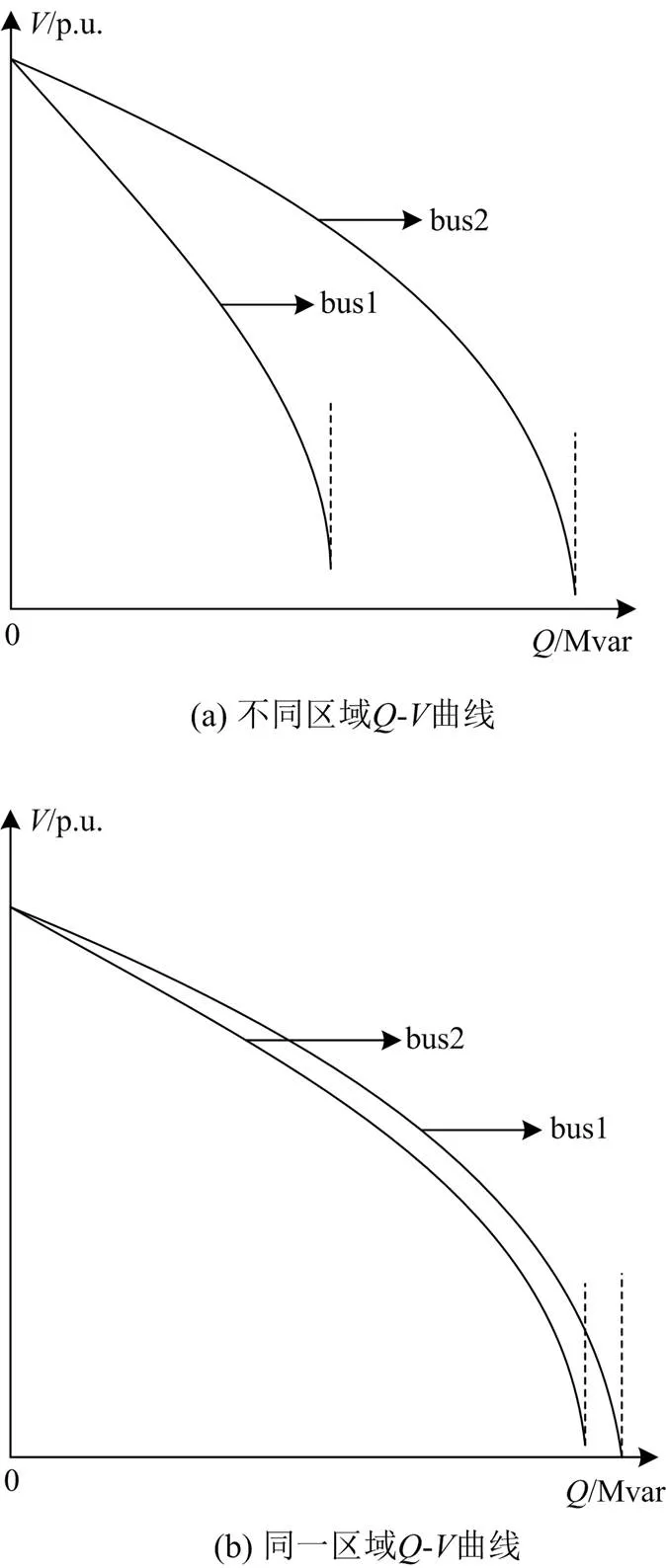
图1 系统Q-V曲线的对比图

1.2 小元素去除与阈值划分

为了得到阈值划分模型，首先利用极坐标下牛顿-拉夫逊法潮流计算得到系统的注入功率，矩阵形式的表达式为

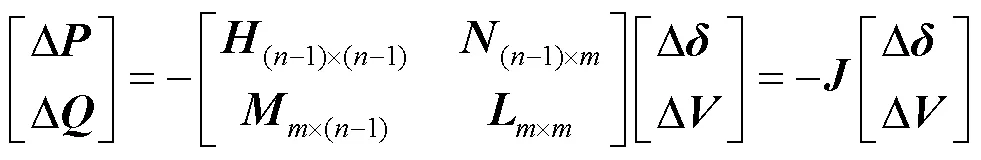
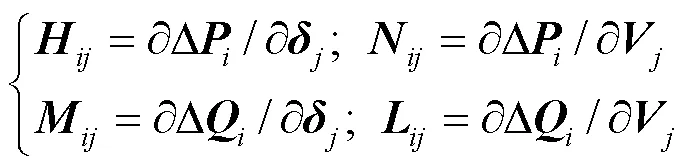
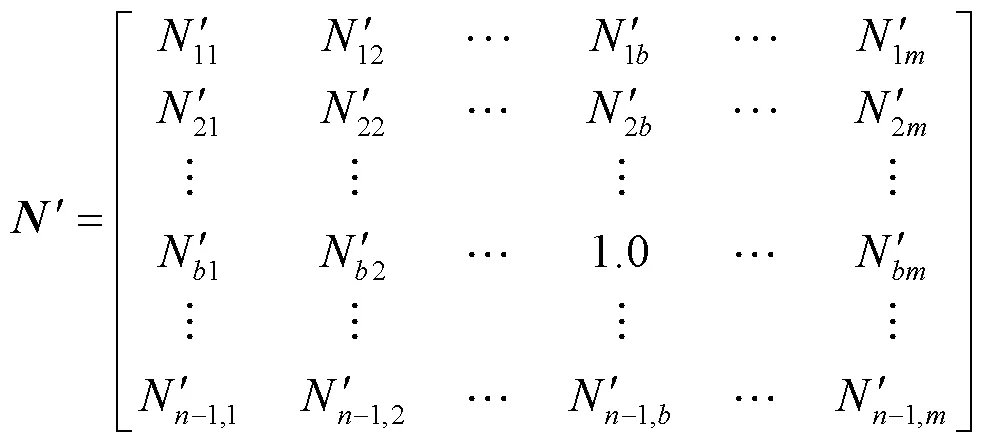
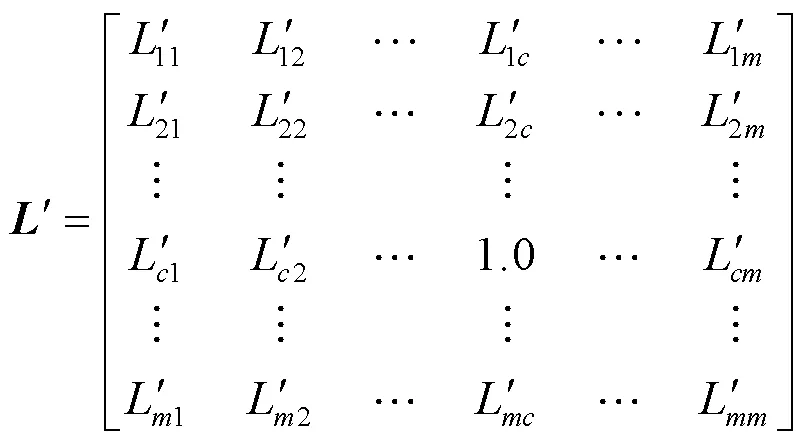
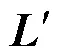
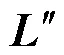
1.3 基于断线扰动的分区边界节点修正法

现有的研究主要是针对随机断线[15-16]、全网负荷支路断线扰动[17]引起的电压波动进行修正。其中，随机断线扰动方法仅计算了随机抽取的支路开断前后的潮流结果，并进行分区修正，不能准确识别并修正电网的薄弱节点；全网负荷支路断线扰动方法需要计算所有支路开断前后的电网潮流结果，再根据电压变化范围进行分区修正，计算量过大。

本文提出了一种更简化的修正方法，不仅能够准确识别出电压薄弱节点，而且只需要计算边界支路开断前后的电压变化范围，就可以优化分区结果，修正后的分区结果中节点的电压波动范围一致。

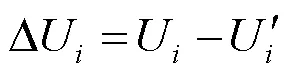
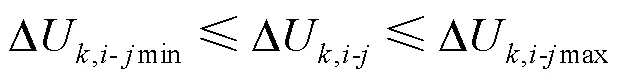
4) 对于独立的节点，若它与相邻区域电压变化相似(相似度采用文献[16]提出的1%)，则将其归为同一区域，若不相似，则单独划为一个区域。

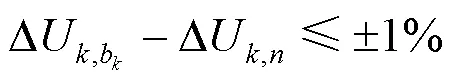
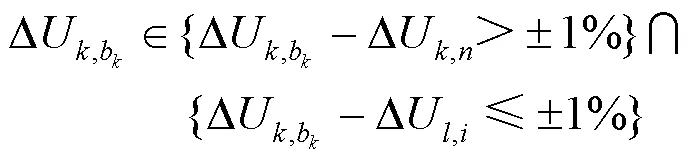
8) 如果两个或多个区域内部节点电压变化均相似，则合并为一个区域。

9) 如果存在独立的节点它们的电压变化量相近，但与已经形成的VCA的电压变化不一致，则将这些独立的节点合并为一个新的区域。

10) 经过步骤1)—步骤9)后，若仍然存在未被合并的无功源节点，应通过节点类型转换将其设置为PQ节点，计算此节点相对于其他区域的平均电气距离，以平均电气距离的大小归并这些节点。

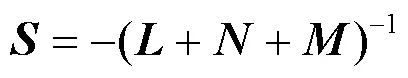
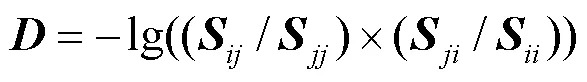
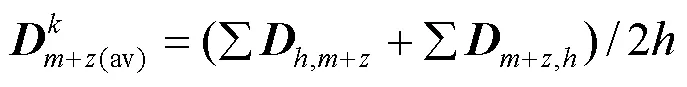
对于平衡节点，若未修正之前的准分区中平衡节点已经归并，则不再处理。若平衡节点仍未归并，将平衡节点的类型转换为PQ 节点，并选择一个电压等级与之接近的电源节点作为新的平衡节点。

由于电气距离的划分是基于区域节点电压对无功资源的灵敏性进行划分，因此，所提方法以负荷节点相对于各VCA的平均电气距离为基础来归并修正后剩余的无功源节点，相比于传统靠人工判断的就近归并方法更具有理论支撑。

2  分区模型及分区修正流程

2.1 改进的阈值划分模型

根据VCA的定义，同一个区域内的扰动导致各节点电压响应一致。在潮流计算中，一般认为电压功角只与有功有关，幅值与无功有关。但是实际情况下在接近静态稳定极限时，有功对电压幅差、无功对电压相差也会产生微弱的影响，这里称之为“弱耦合作用”。

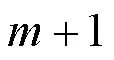
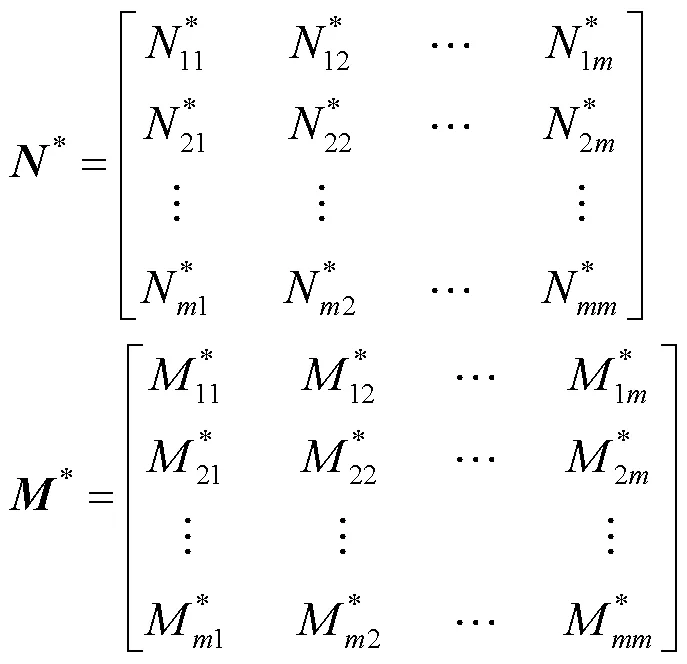
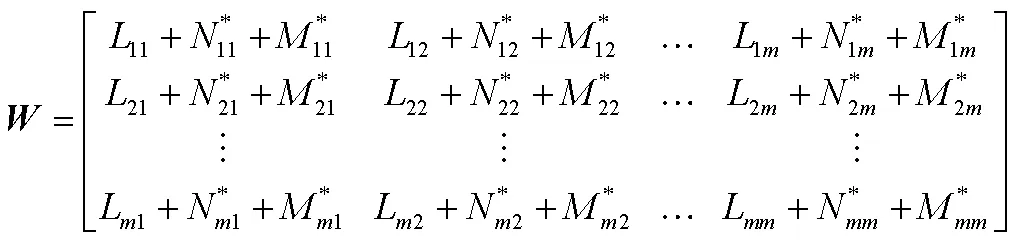
2.2 VCA划分流程

基于边界节点修正的具体分区流程如图2所示。

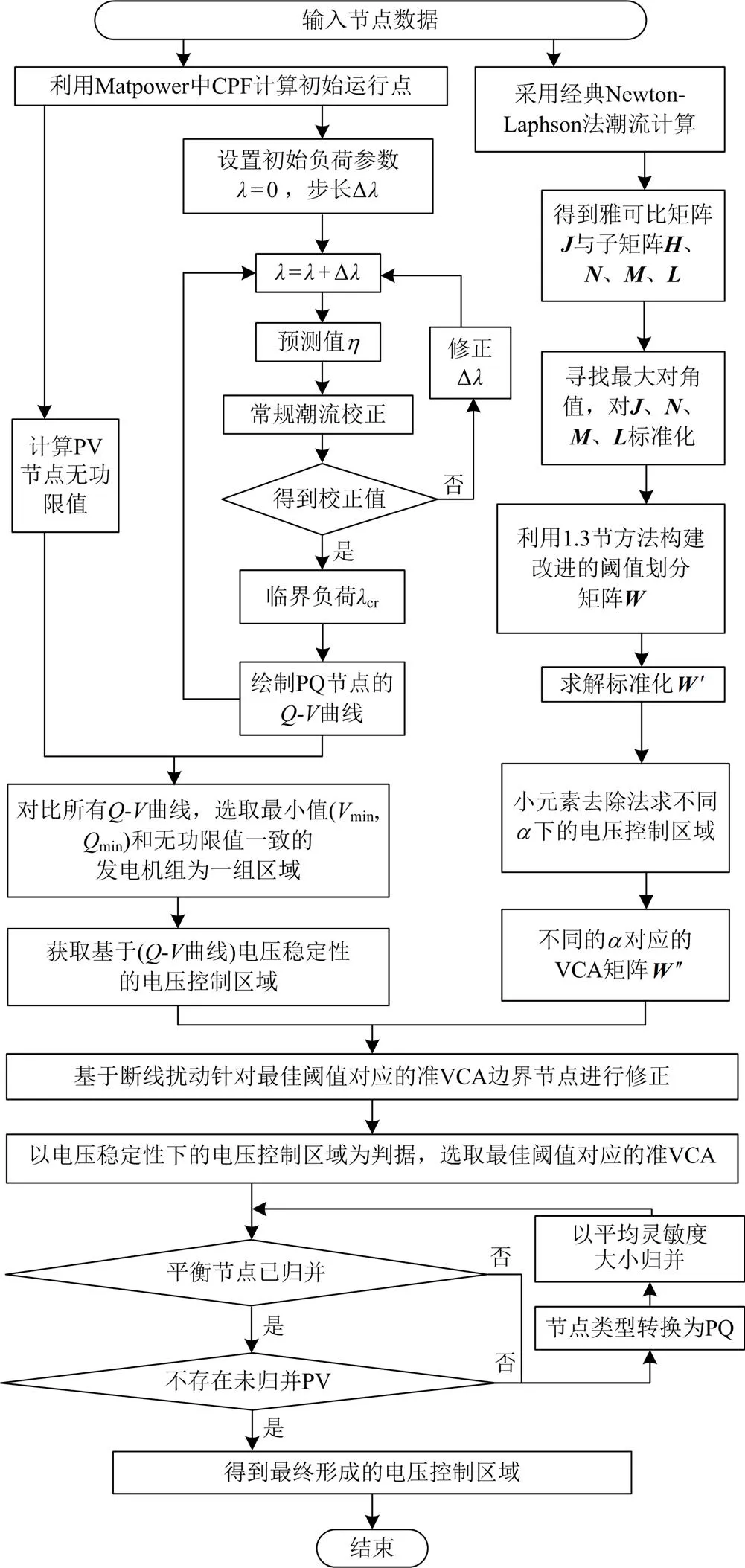
图2 VCA划分及修正流程图

3  算例分析

新英格兰10机39节点系统[23]含29个负荷节点，10个无功源节点，46条支路。以该系统作为算例，利用Matlab编程分析，验证所提方法的合理性。

3.1 Q-V曲线法

为获得最佳阈值对应的准VCA，需要以-曲线法作为划分依据。采用-曲线法，对比所有负荷节点-曲线，可以确定VCA内负荷节点对应的无功源，实现整个电网的稳定分区。

表1为负荷节点曲线的极小值与在该点达到无功限值一致的发电机组共同形成的VCA，可作为确定最佳阈值的判据。

表1 Q-V曲线法得到的划分依据

3.2 小元素去除与阈值划分

小元素去除方法是阈值划分的关键步骤，元素数值的微小改变有可能对划分结果产生影响。因此，不能采用全雅可比矩阵作为阈值划分矩阵。

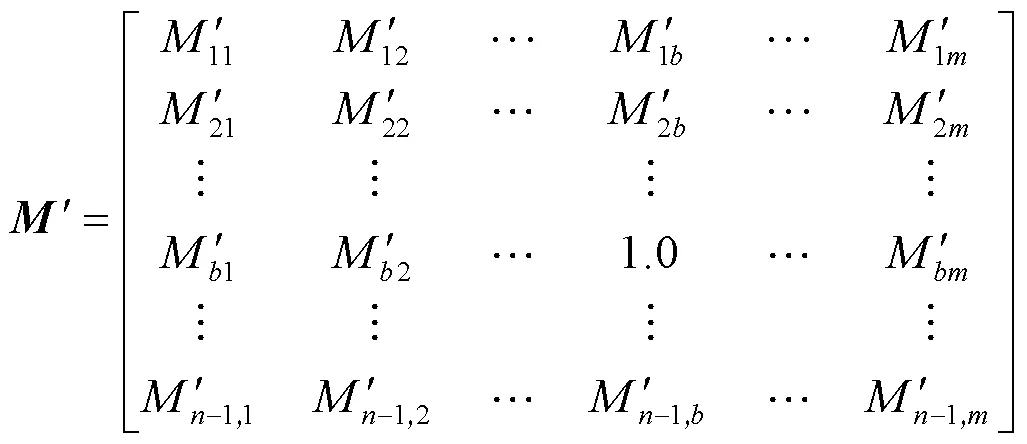
文中将阈值划分矩阵以sparse函数的模式呈现，与full函数得到的矩阵对照分析，能够更清晰地确定小元素的具体位置。小元素去除的过程仅针对非对角元素，表2提取了矩阵中7个较大与7个较小的非对角元素以及、矩阵对应位置的元素，能综合反映所提方法的合理性，具体原因如下。

表2 L矩阵部分元素与N、M对应位置元素

1)矩阵主要反映的是无功功率对电压幅值的控制，代表着节点之间联系的紧密性与系统的电压稳定性。对比表2中的各矩阵元素，绝大部分矩阵的元素远远大于对应位置、矩阵的元素。所以、矩阵的加入不会淹没无功对电压的主要作用，更不会影响区域电压稳定性。

2) 分析从、、矩阵提取的非对角元素，靠近对角线的非对角元素数值较大，远离对角线的非对角元素较小。小元素去除顺序按照由小到大进行，矩阵中大部分靠近对角线的非对角元素远远大于、矩阵对应位置的元素，远离对角线的非对角元素接近、矩阵对应位置的元素。因此，新构建的阈值矩阵划分结果与划分结果基本一致。

3) 由表2可知，矩阵中远离对角线的非对角元素与对应位置的、矩阵元素差距不大，那么这些位置不可以忽略无功对电压相差和有功对电压幅差的影响。因此，文中利用、、矩阵中负荷维度相加来体现功率对电压的弱耦合关系。

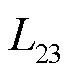
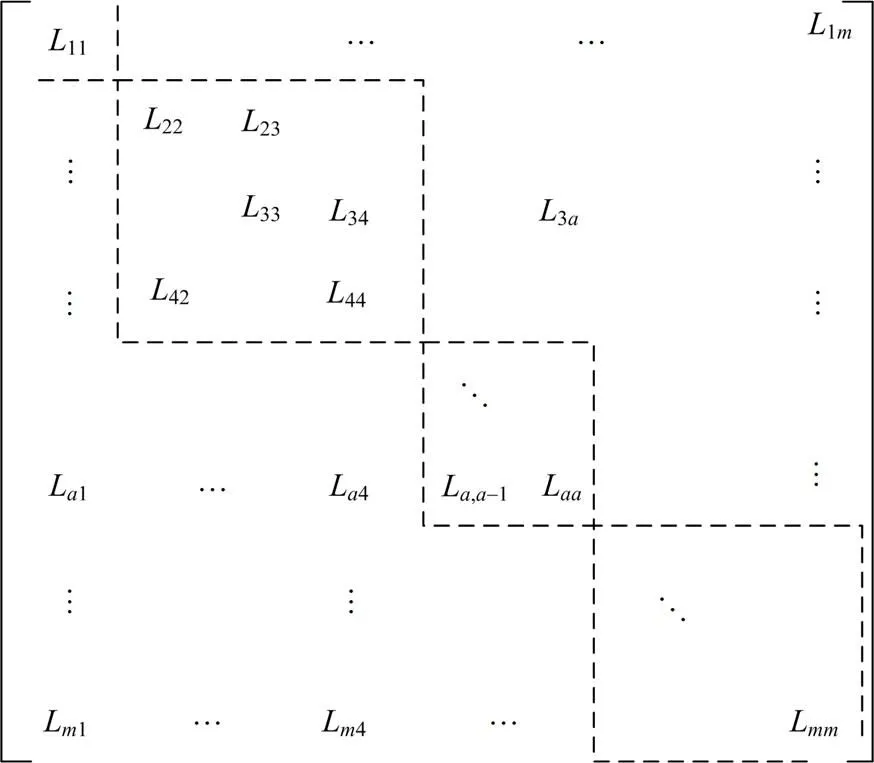
图3 雅可比子矩阵的非对角元素图

综上，在阈值划分模型中加入、矩阵元素不仅不会影响电压控制区域的划分，还能综合考虑功率与电压的弱耦合作用，不会造成系统无功短缺，比单纯考虑矩阵的划分更合理。

表3 不同阈值划分下的VCA

Table 3 VCA under different thresholds

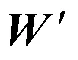
分区数量由28缩减到19的过程中，对应的所有阈值之间的差值分别为0.0855、0.1331、0.1955，比阈值之间的差值0.0877、0.1736、0.2369要小，可以避免微小数值元素被忽略或非对角较小元素的计算误差。而分区数量由18缩减到14的过程中，模型对应阈值差值较大，说明对应阈值划分的区分度更大，区分度越大分区越准确。

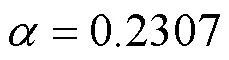
3.3 VCA边界节点修正划分

图4为39节点系统准分区区域边界支路的断线位置。

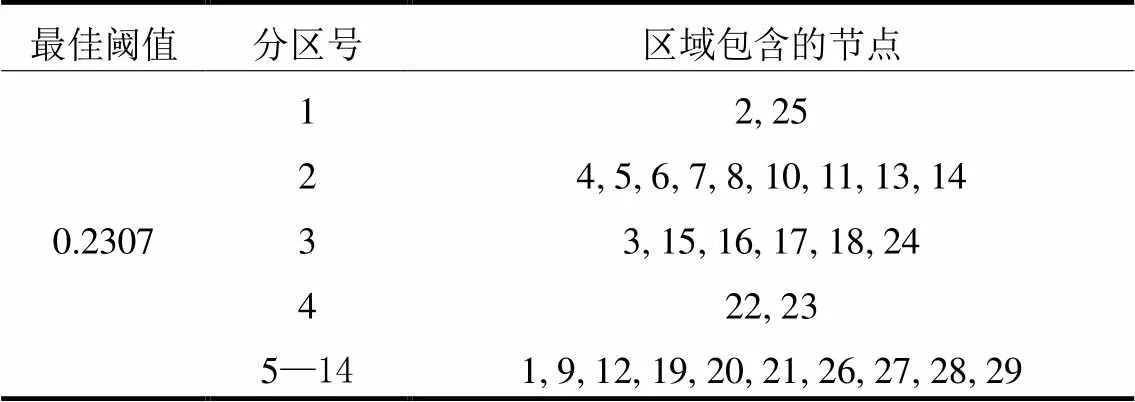
表4 最佳阈值对应的准VCA

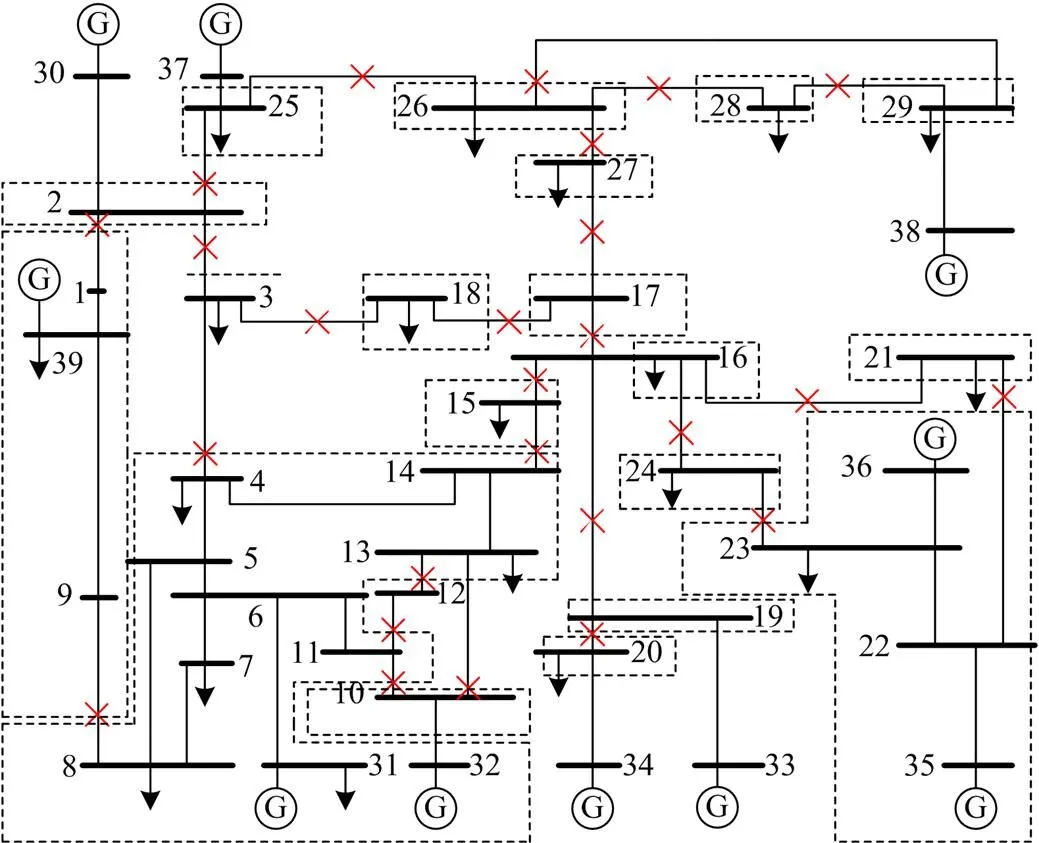
图4 39节点系统VCA边界节点断线位置

由图4可知，VCA断线的位置在准VCA的边界支路上。

表5为新方法与传统方法的断线节点。

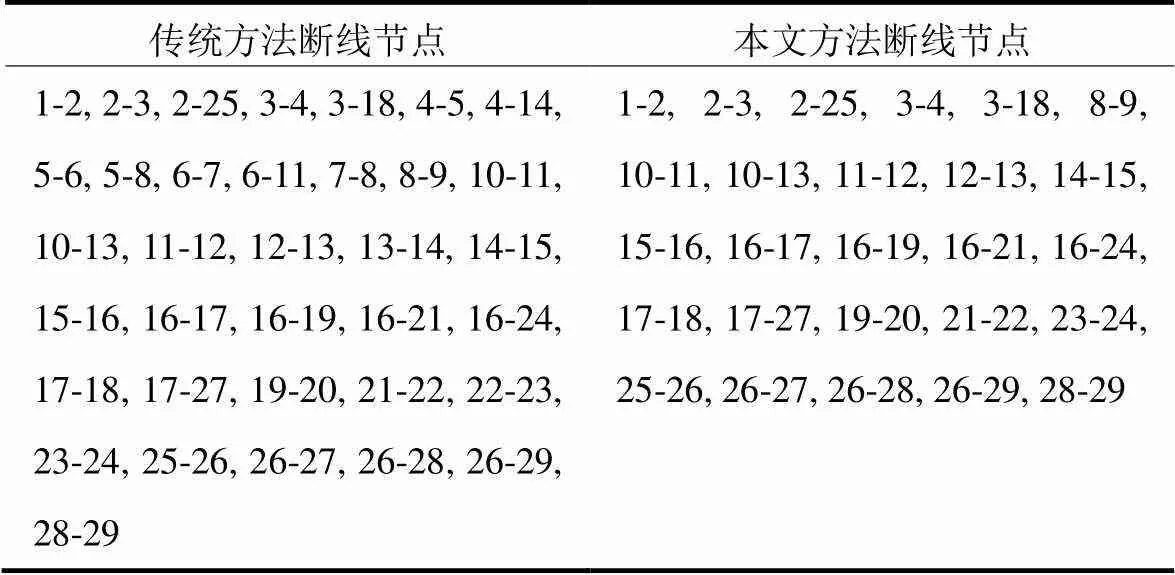
表5 新方法与传统方法的断线节点

结合图4与表5可知，对比传统方法的断线节点可知，本文所提的进行VCA边界节点断线修正的方法计算量小，仅针对26个边界支路进行断线修正即可，而传统方法需要计算35条负荷支路断线前后的潮流。由此可以预测，在节点越多的系统中边界节点的占比越大，减少的断线计算量越大。

将线路对应节点按电压变化由大到小排序修正，依次为21-22、15-16、2-3，当修正至2-3时，修正结果不再改变。由表6可知，本文方法能够在减少计算断线数量的前提下得到与传统方法一致的修正结果。

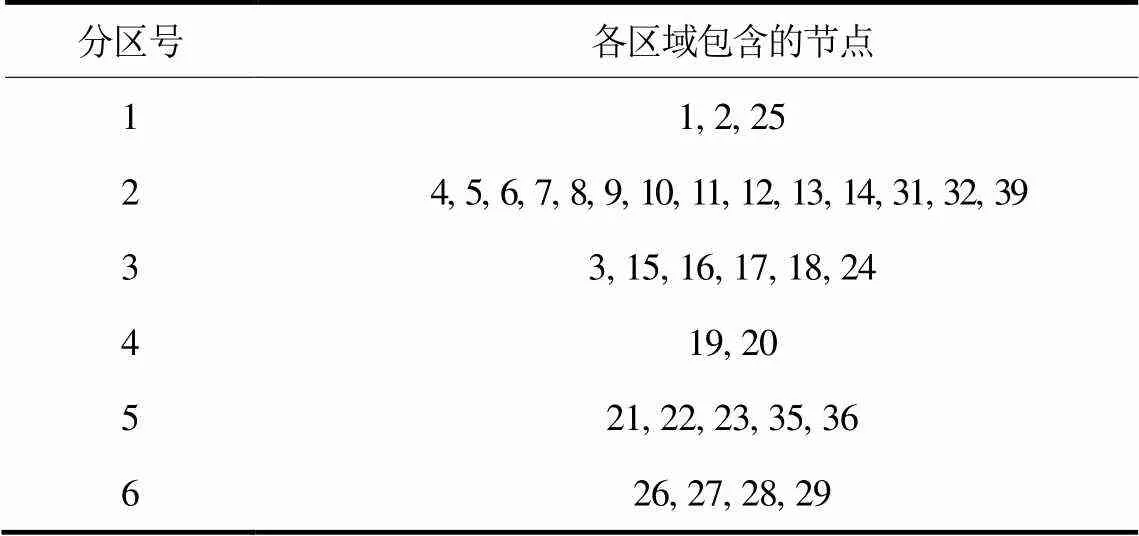
表6 利用边界节点修正后的39节点系统VCA划分

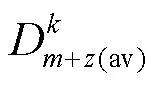
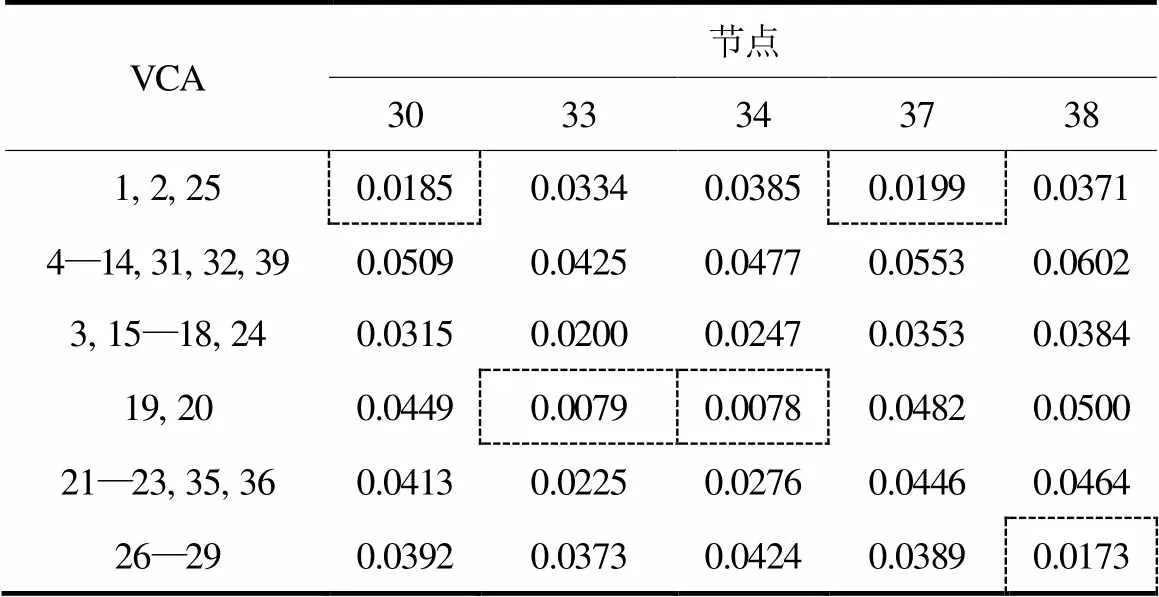
表7 利用平均电气距离归并剩余PV节点

由表7可知，30、33、34、37、38节点分别归并于3个不同区域，最终分区结果如表8所示。

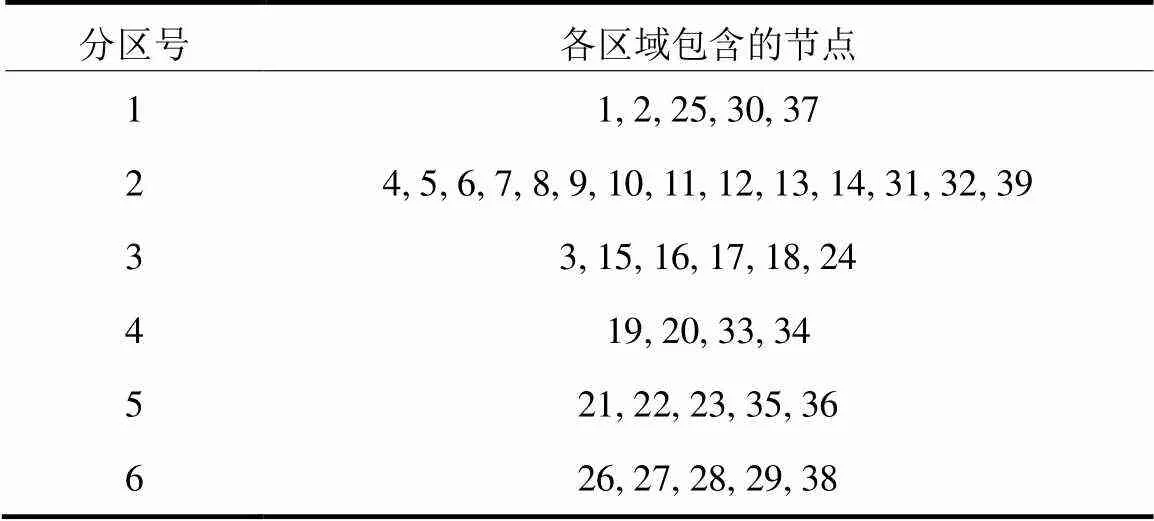
表8 边界修正与PV归并后的VCA

所提修正方法避免了计算整个系统负荷断线的复杂过程。修正后的IEEE39节点网络拓扑分区如图5所示，分区结果既满足了无功源的控制能力，又体现了区域的连通性，分区结果稳定可靠，适用于解决复杂电网分区问题。

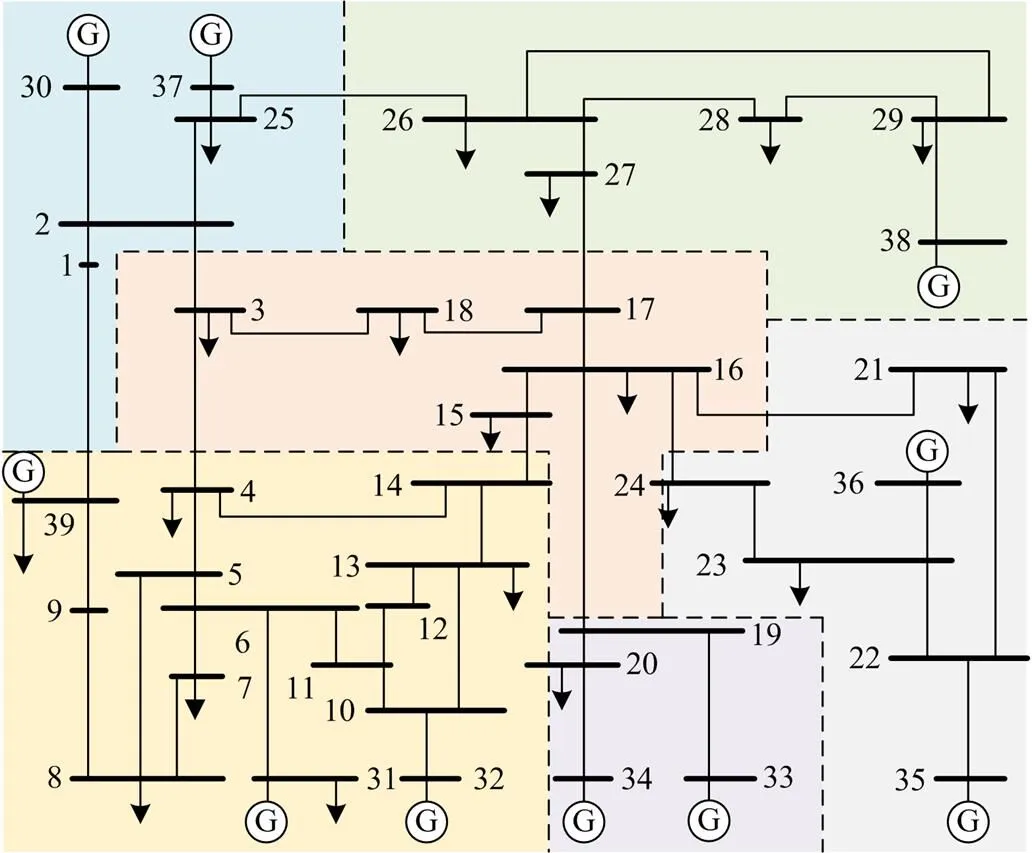
图5 IEEE39节点网络拓扑分区图

4  结论

针对分区后电压变化不一致的问题，本文提出了一种基于边界节点的VCA修正方法。具体改进措施与意义如下。

1) 采用的阈值划分矩阵，综合考虑了有功对电压幅差、无功对电压相差的偏导，在不影响无功对电压的强耦合作用下体现了节点之间电气联系的弱耦合性。

2) 采用断线扰动分析法，针对VCA边界节点进行修正。该方法能够减少负荷断线的数量，从而减少传统分区修正方法的计算量，提高了分区修正的效率。

3) 采用平均电气距离法处理了剩余PV节点的归并问题，相比传统方法的就近归并更具有理论依据。

算例分析结果表明，分区结果的可靠性高，既满足了区域电压稳定性条件，又满足了系统节点区域划分的地理邻近性。

[1] BABU R, RAJ S, BHATTACHARYYA B. Weak bus- constrained PMU placement for complete observability of a connected power network considering voltage stability indices[J]. Protection and Control of Modern Power Systems, 2020, 5(4): 294-307.

[2] 钟俊, 焦兴伟, 王志川. 基于电压临界稳定状态下的无功电压分区方法[J]. 电网技术, 2019, 43(10): 3761-3768.

ZHONG Jun, JIAO Xingwei, WANG Zhichuan. Reactive voltage partition method based on voltage critical steady state[J]. Power System Technology, 2019, 43(10): 3761-3768.

[3] JI H, LI P, JI J, et al. MPC-based local voltage control strategy of DGs in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2911-2921.

[4] 辛建波, 杨程祥, 舒展, 等. 基于静态安全域的交直流混联大电网关键线路辨识[J]. 电力系统保护与控制, 2020, 48(6): 165-172.

XIN Jianbo, YANG Chengxiang, SHU Zhan, et al. Identification of critical lines in AC/DC hybrid large power grid based on steady-state security region[J]. Power System Protection and Control, 2020, 48(6): 165-172.

[5] 赵晶晶, 贾然, 陈凌汉, 等. 基于深度学习和改进K-means聚类算法的电网无功电压快速分区研究[J]. 电力系统保护与控制, 2021, 49(14): 89-95.

ZHAO Jingjing, JIA Ran, CHEN Linghan, et al. Research on rapid zoning of power grid reactive power and voltage based on deep learning and improved K-means clustering algorithm[J]. Power System Protection and Control, 2021, 49(14): 89-95.

[6] DING J, ZHANG Q, HU S, et al. Clusters partition and zonal voltage regulation for distribution networks with high penetration of PVs [J]. IET Generation, Transmission & Distribution, 2018, 12(22): 6041-6051.

[7] 姜涛, 陈厚合, 李国庆. 基于局部电压稳定指标的电压/无功分区调节方法[J]. 电网技术, 2012, 36(7): 207-213.

JIANG Tao, CHEN Houhe, LI Guoqing. Voltage/reactive power division adjustment method based on local voltage stability index[J]. Power System Technology, 2012, 36(7): 207-213.

[8] 徐正清, 肖艳炜, 李群山, 等. 基于灵敏度及粒子群算法的输电断面功率越限控制方法对比研究[J]. 电力系统保护与控制, 2020, 48(15): 177-186.

XU Zhengqing, XIAO Yanwei, LI Qunshan, et al. Comparative study of transmission section power over-limit control methods based on sensitivity and particle swarm algorithm[J]. Power System Protection and Control, 2020, 48(15): 177-186.

[9] 郑晓莹, 陈政轩, 曾琮. 含分布式电源的配电网双层分区调压策略[J]. 电力系统保护与控制, 2021, 49(6): 90-97.

ZHENG Xiaoying, CHEN Zhengxuan, ZENG Cong. Double-layer partition voltage regulation strategy for distribution network with distributed generation[J]. Power System Protection and Control, 2021, 49(6): 90-97.

[10] JAY D. Isoperimetric clustering-based network partitioning algorithm for voltage-apparent power coupled areas[J]. IET Generation, Transmission & Distribution, 2019, 13(22): 5109-5116.

[11] DING J, QIAN Z, WANG Q, et al. Clusters partition and zonal voltage regulation for distribution networks with high penetration of PVs[J]. IET Generation, Transmission & Distribution, 2018, 12(22): 1-9.

[12] ANDALIB-BIN-KARIM C, LIANG X, KHAN N, et al. Determine Q-V characteristics of grid-connected wind farms for voltage control using a data-driven analytics approach[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4162-4175.

[13] 刘海涛, 许伦, 郝思鹏, 等. 基于配电网分区的分布式混合储能优化方法[J]. 电力自动化设备, 2020, 40(5): 180-188.

LIU Haitao, XU Lun, HAO Sipeng, et al. Optimization method of distributed hybrid energy storage based on distribution network partition[J]. Electric Power Automation Equipment, 2020, 40(5): 180-188.

[14] 颜伟, 杨彪, 莫静山, 等. 交直流系统主导节点选择与无功分区的概率优化方法[J]. 中国电力, 2020, 53(8): 77-84.

YAN Wei, YANG Biao, MO Jingshan, et al. Probabilistic optimization method for pilot-bus selection and network partitioning of AC/DC system[J]. Electric Power, 2020, 53(8): 77-84.

[15] PRYOR L, COLLINS G. Voltage stability based formation of voltage control areas considering impact of contingencies[J]. International Journal of Applied Power Engineering, 2012, 1(3): 287-339.

[16] AND M K V, SRIVASTAVA S C. Approach to determine voltage control areas considering impact of contingencies[J]. IEE Proceedings Part C Generation Transmission & Distribution, 2005, 152(3): 342-350.

[17] 冯光明, 陆超, 黄志刚, 等. 基于雅可比矩阵的电压控制区域划分的改进[J]. 电力系统自动化, 2007, 31(12): 7-11.

FENG Guangming, LU Chao, HUANG Zhigang, et al. Improvements on voltage control area partition based on Jacobian matrix[J]. Automation of Electric Power Systems, 2007, 31(12): 7-11.

[18] 张旭, 陈云龙, 王仪贤, 等. 基于潮流断面修正的含风电电网无功-电压分区方法[J]. 电力自动化设备, 2019, 39(10): 8-15.

ZHANG Xu, CHEN Yunlong, WANG Yixian, et al. Reactive power-voltage partitioning of power grid with wind power based on correction of power flow section[J]. Electric Power Automation Equipment, 2019, 39(10): 8-15.

[19] SCHLUETER R A, HU I P, CHANG M W, et al. Methods for determining proximity to voltage collapse[J]. IEEE Transactions on Power Systems, 1991, 6(1): 285-292.

[20] SCHLUETER R A. A voltage stability security assessment method[J]. IEEE Transactions on Power Systems, 1998, 13(4): 1423-1438.

[21] 张晓英, 蒋拯, 丁宁, 等. 负荷裕度及其与典型参数的灵敏度计算[J]. 电机与控制学报, 2015, 19(8): 28-35.

ZHANG Xiaoying, JIANG Zheng, DING Ning, et al. Load margin and its sensitivity calculation with typical parameters[J]. Journal of Electrical Machines and Control, 2015, 19(8): 28-35.

[22] LIE T, SCHLUETER R A. Method of identifying weak transmission network stability boundaries[J]. IEEE Transactions on Power Systems, 1993, 8(1): 293-301.

[23] 冒波波, 施昱青, 彭飞. 基于容积卡尔曼滤波残差驱动的动态电力系统态势感知方法研究[J]. 供用电, 2020, 37(8): 39-46.

MAO Bobo, SHI Yuqing, PENG Fei. Research on dynamic power system situational awareness method based on volumetric Kalman filter residual drive[J]. Distribution & Utilization, 2020, 37(8): 39-46.

[24] 李英量, 王康, 王德明, 等. 考虑弱耦合关系的全维灵敏度矩阵快速VCA方法[J]. 电测与仪表, 2022, 59(1): 69-76.

LI Yingliang, WANG Kang, WANG Deming, et al. A fast VCA method for full-dimensional sensitivity matrix considering weak coupling relations[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 69-76.

[25] ZHONG J, NOBILE E, BOSE A, et al. Localized reactive power markets using the concept of voltage control areas[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1555-1561.

A method for correcting boundary nodes of a voltage control region based on disconnection disturbance

LOU Qihe1, WANG Kang2, YUAN Tiejiang2, DONG Litong2, 3

(1. State Grid Corporation of China, Beijing 100031, China; 2. School of Electrical Engineering,Dalian University of Technology, Dalian 116024, China; 3. State Grid Economic and Technology Research Institute Co., Ltd., Beijing 102209, China)

The voltage control area (VCA) has weak coupling, and correcting the VCA can improve the consistency of voltage changes in the area, thereby optimizing the results of grid partitioning.The traditional partition correction method has problems such as requiring a large amount of calculation and lack of a theoretical basis for PV node merging. Therefore, this paper proposes a method to correct the boundary nodes of the VCA, one which can effectively reduce the calculation for the partition correction.The proposed method uses small element removal to obtain the grid division results under each threshold, and uses the Q-V curve as the criterion to select the quasi-division corresponding to the best threshold in each division result. Based on the weak coupling between regions, the proposed method is used to correct the quasi-partitioning, and the optimized partitioning results are obtained.The proposed method performs disconnection correction on the boundary nodes of the quasi-partition, and uses the average electrical distance to merge the remaining PV nodes after correction. This not only reduces the calculation for the partition correction, but also provides a theoretical basis for the rational allocation of reactive power sources in each area.The effectiveness of the proposed method is verified by simulation analysis of 10 machines and 39 nodes in New England.

disconnection disturbance; voltage control area; threshold analysis; average electrical distance; voltage stability

10.19783/j.cnki.pspc.211470

2021-11-01；

2022-05-11

娄奇鹤(1978—) ，男，博士，高级工程师，主要研究方向为新能源发展战略、并网管理、经济管理理论和方法；E-mail: qihe-lou@sgcc.com.cn

王 康(1996—)，男，通信作者，博士研究生，主要研究向为无功电压控制分区、电网规划；E-mail: 940383184@ qq.com

袁铁江(1975—)，男，博士，教授、博导，主要研究方向为电力系统优化调度，氢能与化石能源。E-mail: ytj1975@ dlut.edu.cn

国家电网有限公司总部管理科技项目资助“高比例新能源区域电网消纳受阻因素智能辨识及辅助决策研究”(5108-202135033A-0-0-00)

This work is supported by the Management Science and Technology Project of the Headquarters of State Grid Corporation of China (No. 5108-202135033A-0-0-00).

(编辑 许 威)