MIMO系统中的非常数模半盲均衡方案*
肖可馨,李 晖,2,周又玲,王 萍,林志阳
(1.海南大学 信息与通信工程学院,海口 570228;2.南京信息工程大学滨江学院,江苏 无锡 214105)
0 引 言
多输入多输出(Multiple-Input Multiple-Output,MIMO)技术,作为近年来无线通信方式的一大热点,被认定为5G系统的关键技术。作为现代通信中的巨大突破,MIMO允许在收、发端同时使用多个天线接收、发送多个空间流,利用相关技术和多径传输,建立空间平行传输通道。考虑到MIMO无线通信中信道衰落、随机噪声、空间多径效应等影响,每对天线传输过程中会产生大量检测错误。
到目前为止,陆地信道中往往采用各种均衡技术对发送信号进行恢复。传统的线性自适应均衡技术需要发送训练序列,虽然计算简单、均衡性能良好,但是频谱资源利用率较低。而盲均衡技术无需训练序列,可有效解决前者占用较大带宽的问题,但同时会增加计算复杂度以及降低均衡性能。半盲均衡技术[1-3]综合线性自适应均衡技术和盲均衡技术的优点,可利用各种先验信息估计均衡器初始值,结合盲均衡算法得到最优均衡器。
考虑单小区大规模MIMO系统中用户与基站间的各种衰落[4],文献[5]提出了两种基于期望最大化(Expectation Maximization,EM)估计的半盲迭代改进算法,降低了计算复杂度并减少了导频开销,相比导频估计的极大似然(Maximum Likelihood,ML)算法[6],优化了系统的均方误差。
目前大部分的研究都是在陆地背景下采用盲均衡或半盲均衡算法校正已失真的信号波形。本文提出可采用结合MIMO信道先验特性的方法来实现半盲均衡算法,构建完整的MIMO系统的半盲时域均衡模型。在满足瑞利分布的MIMO无线信道的基础下,进一步研究如何在近距离陆地传输过程中减小盲均衡的剩余稳态误差,降低计算复杂度,更好地均衡传输信号,并提出了一种改进的非常数模(Non-constant Modulus Algorithm,NCMA)半盲均衡方案。该方案结合了MIMO信道先验知识,同时又提升了频谱资源利用率,即能提高移动通信的质量。理论分析和计算机仿真证明,改进后的算法能通过控制变步长减小剩余稳态误差,加快收敛速度,改善信道均衡效果。因此,该算法更适用于MIMO无线信道的均衡处理。
1 MIMO系统的均衡模型
1.1 MIMO无线信道模型的构建
在MIMO信道中,每个子信道的传输系数都服从于某种共同的分布,可以是瑞利分布、莱斯分布或高斯分布,其随机的传输系数最后构成了MIMO信道矩阵。通常情况下,发射机和接收机在近距离陆地传输过程中,不存在直射视距(Line-of-Sight,LoS)的情况,而仅存在反射、折射或衍射的情况。因此,本文考虑的信道服从独立瑞利衰落[7-8]。
如图1所示的MIMO系统中,发射端采用Nt×1个天线,接收端采用Nr×1个天线,两端均采用等距离线性阵列。
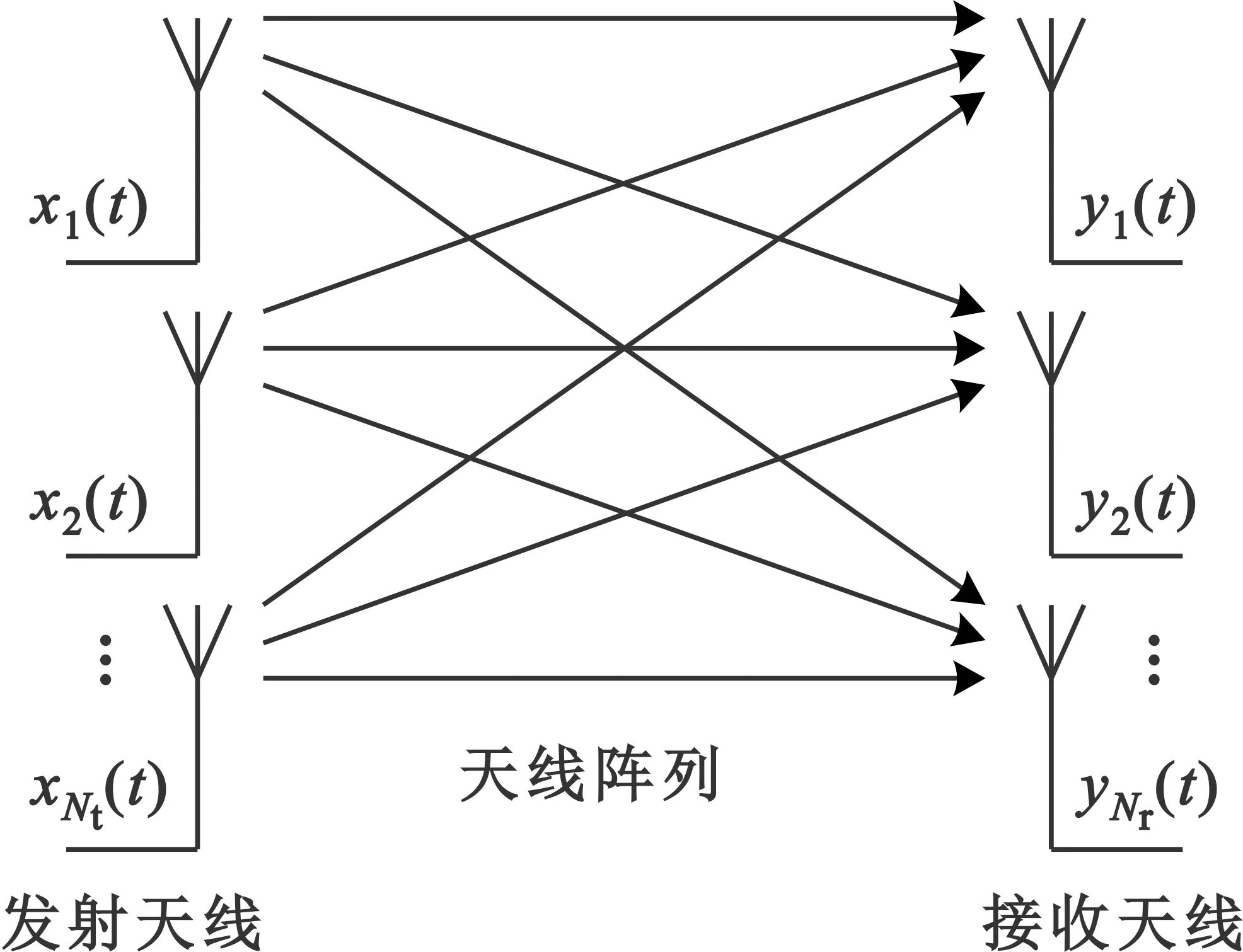
图1 MIMO系统示意图
假设发射端天线阵列上的信号表示为Nt×1维列向量Xi(t),即
Xi(t)=[x1(t),x2(t),x3(t),…,xNt(t)]T。
(1)
式中:xi(t)表示第i根发射天线信号,[ ]T表示矢量的转置。假设接收端天线阵列上的信号表示为Nr×1维列向量Yj(t),即
Yj(t)=[y1(t),y2(t),y3(t),…,yNr(t)]T。
(2)
式中:yj(t)表示第j根接收天线信号。假设从发射端出发至接收端的多个天线均服从独立的瑞利衰落,对于Nr×Nt的天线阵列,其随机信道矩阵为H,表示为
(3)
式中:hji(i=1,2,…,Nt;j=1,2,…,Nr)表示第j根接收天线信号与第i根发射天线信号,即信道中收、发天线之间的衰落系数。因此,系统中的接收信号可表示为
Y=HX+Z。
(4)
式中:Z为Nr×1维加性高斯白噪声。经过瑞利信道,第j根接收天线接收到的信号yj(t)具体可表示为
yj(t)=cos(ωct)Ij(t)-sin(ωct)Qj(t)+nj(t)。
(5)
式中:ωc为正弦载波信号的频率,nj(t)为接收端噪声。根据中心极限定理,大量独立随机变量之和的分布将趋于正态分布。因此,本文Ij(t)和Qj(t)均值取0,方差σ2相等,这种表示方式也被称为同相-正交表示法[9]。已知以上条件,使用包络-相位表示法,接收端复包络Vj(t)的大小以及相位φj(t)按瑞利分布可表示为
(6)
(7)
1.2 MIMO系统组合时域均衡器模型的构建
由于均衡技术是一种可有效补偿因MIMO通信导致信号失真的方法,因此可将均衡技术运用于MIMO通信中。其中时域均衡可通过调节整个内在系统的冲激响应来满足无码间干扰(Inter-symbol Interference,ISI)条件,即可直接校正已失真的响应波形。相比于频域均衡,它更易实现,简单且均衡效果更好。因此本文采用时域均衡器,后文涉及到的均衡算法都是在时域均衡器的基础上实现。图2是MIMO系统组合时域均衡器的原理框图,该系统输入4-QAM调制方式的信号,经过上文构建的MIMO信道,运用时域均衡器直接校正已失真的信号波形。
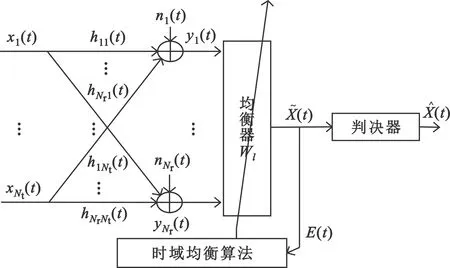
图2 MIMO系统组合时域均衡器原理框图
该系统最早输入4-QAM信号的矢量表达式为
xi(t)=xi1f1(t)+xi2f2(t),i=1,2,…,4,
(8)
即表示xi1和xi2两个独立的基带数字信号对两个互相正交的同频载波基函数f1(t)和f2(t)进行抑制载波的双边带调制。
将已经过正交振幅调制、功率归一化的信号xi(t)输入服从瑞利衰落的MIMO信道,系统中接收信号yj(t)也可改写为
(9)
式中:yj(t)(j=1,2,3,…,Nr)也为均衡器的输入信号,i=1,2,3,…,Nt。在信号的传输过程中,尤其是在多天线传输中存在着大量的电磁波、空间散射物质、噪音以及路径间干扰,这些因素会影响从发到收的信号,使得天线接收端的信号出现严重失真,进而影响整个系统传输数据的真实性和可靠性,使通信质量下降甚至不可用。因此,经MIMO信道传输后的接收信号yj(t)必须通过均衡器来校正信号错误。假设均衡器上的抽头系数表示为L×1维列向量Wl(t):
Wl(t)=[w1(t),w2(t),w3(t),…,wL(t)]T。
(10)
式中:wl(t)表示第l个均衡器抽头加权系数。因此,均衡器输出函数可表示为
(11)
2 半盲时域均衡算法
2.1 常数模半盲均衡算法
盲均衡技术或半盲均衡技术常常被广泛运用于MIMO无线通信中,用来解决MIMO系统通信过程中的多径效应、ISI以及噪声等问题。其中常数模算法(Constant Modulus Algorithm,CMA)半盲时域均衡器原理框图如图3所示。半盲时域均衡器模型是在盲均衡器和自适应均衡器的基础上进行改进的模型,它的原理框图与盲均衡原理框图类似。大多数半盲均衡器设计偏于采用少量训练序列的方法,再结合盲均衡算法来实现半盲均衡算法。下文提出的CMA算法就是在半盲均衡器上实现的。
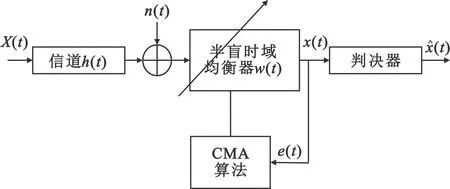
图3 常数模半盲时域均衡器原理框图
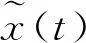
MSE=J(t)=e(t)2。
(12)
式中:e(t)为误差函数,
(13)
本文算法采用最小均方(Least Mean Square,LMS)算法思想,使均衡器权系数迭代公式的每一步更新都能使目标函数值减小。因此,第l个均衡器抽头加权系数迭代公式可定义如下:
(14)
式中:μ为固定步长,在整个迭代过程中为一个常数值。将式(13)代入式(14)中,第l个半盲均衡器抽头加权系数迭代公式可改写为
(15)
2.2 改进的非常数模半盲均衡算法
在先前的大多数研究中,基于少量的训练序列的半盲均衡设计仍存在一些缺点:其一,在实验中依旧考虑训练样本,无法良好解决计算复杂度和占用较大带宽的问题;其二,仅依赖训练样本的半盲均衡方案设计,无法体现均衡器与MIMO无线信道的关联,实验方法不太适用于本文MIMO系统的研究。因此,本文对先前半盲均衡做进一步改进,提出一种结合MIMO信道先验特性的半盲均衡方案,该方案关联MIMO信道参数对均衡器初始值进行预设。
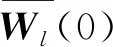
(16)
式中:hji(i=1,2,…,Nt;j=1,2,…,Nr)表示第j根接收天线信号与第i根发射天线子信道冲激响应,[ ]-1表示求矢量的逆,均衡器抽头个数l为Nr×Nt。
相比利用尽量少训练序列取得均衡器初始值的方法,该方法通过联合MIMO信道的瑞利衰落系数值预设均衡器初始值,计算更精简,实验数据更能真实反映具有随机时变性的MIMO系统的均衡效果,更适用于MIMO无线信道的均衡处理。另外,CMA算法虽然易实现,计算简单,但由于固定步长的限制,会导致系统在均衡过程中出现收敛慢、收敛后剩余误差大的缺点。因此,有研究者提出NCMA算法的想法,将固定步长转换成一个非线性函数,表示如下:
μ(t)=b[1-e(-a|e(t)|] 。
(17)
由式(17)可知,NCMA均衡算法是在CMA算法的基础上进行改进的,它仍采用最陡梯度下降法,即LMS算法的中心思想来迭代均衡器的抽头系数,逐步寻找均方误差函数的最优解,但权系数迭代公式有所改变,将固定步长μ改为变量。本文为了进一步提高算法的收敛速度,并保持更好的均衡效果,对变步长公式μ(t)做进一步改进,提出了一种改进的NCMA均衡算法。变步长公式表示如下:
(18)
调整式(18)中参数a和b,可灵活实现不同步长下加快算法收敛速度。根据式(18),图4给出了变步长μ(t)与误差e(t)关系。
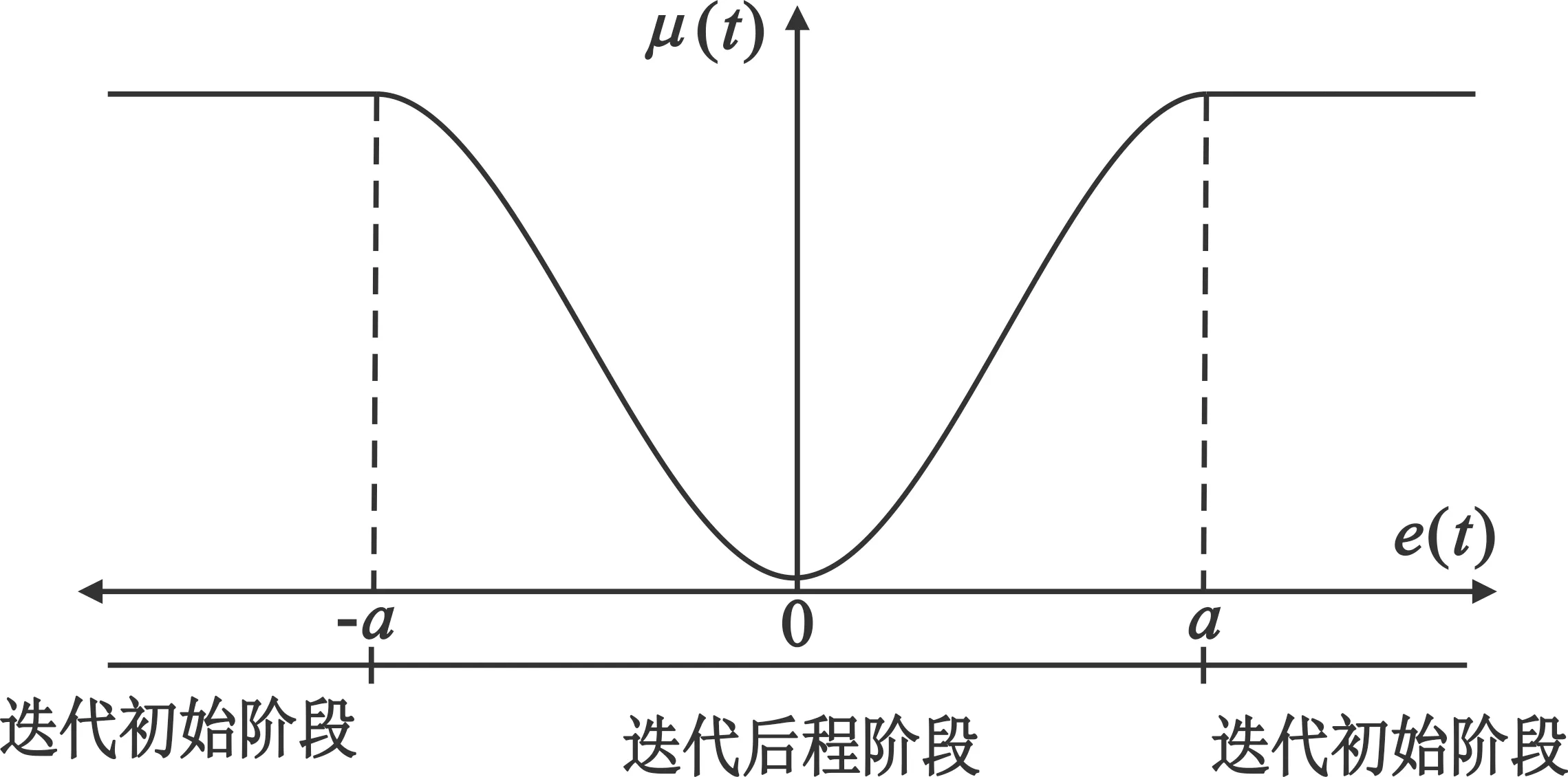
图4 变步长公式与误差关系图
由图4可知,在迭代后程阶段,即误差|e(t)|已较小时,变步长公式满足瑞利分布函数的形式,即式(18)的下面分式,其中a2即方差σ2。在迭代初始阶段,即误差|e(t)|较大时,若仍采用该分式的瑞利分布形式控制步长,变步长μ(t)将趋于下降状态,导致在算法初始阶段步长小,算法收敛慢度慢。本文假设当绝对误差大于标准差σ,即|e(t)|≥a后,将|e(t)|=a代入该分式得到下面的分式,实现误差|e(t)|较大时变步长μ(t)仍能保持较大。
总体来说,对于改进的NCMA均衡算法,在算法的初始阶段,即误差较大时,仍能保持较大的步长提高收敛速度;在算法的后程阶段,即误差已较小时,通过减小步长,有利于降低剩余稳态误差,提高收敛精确度。同时,改进后的变步长公式满足瑞利分布的形式,使得和本文建立的服从独立瑞利衰落的MIMO信道传输特性更吻合,改善均衡性能。
3 仿真与数据分析
3.1 星座图对比
在实验中,MIMO信道接收端天线数量为Nr=2根,发射端天线数量为Nt=4根,信道矩阵服从独立瑞利衰落。信道的输入端采用4-QAM调制方式的信号,发送信源信号总数T=6 000个,信道接收端为高斯白噪声,信噪比(Signal-to-Noise Ratio,SNR)为30 dB。
在以上相同仿真环境下,实验仿真500次。对于每一次实验,均假设半盲均衡器的抽头个数为8个,根据式(16),估计均衡器初始值,均衡器抽头加权系数初始值的设定与MIMO信道冲激响应值互逆,CMA算法的固定步长μ=0.000 4,改进的NCMA算法中参数设定为a=0.8、b=0.009,代入式(18)。星座图仿真结果如图5所示。图5(a)为4-QAM调制输入信号星座图,输入信号满足正交振幅调制。图5(b)为半盲均衡器输入信号星座图,也为MIMO信道接收端信号星座图,由图5(b)可以看出输入信号经过衰落信道和高斯白噪声后,QAM信号星座点明显出现了扩散,星座点已和原始的4个星座点的位置不吻合。图5(c)和图5(d)均为半盲均衡器输出信号星座图,分别采用CMA算法、改进的NCMA算法。由图5(c)和图5(d)可以看出,两种半盲均衡算法均能弥补由MIMO信道传输造成信号严重失真的问题,且均衡效果良好。但比较图5(c)和图5(d)可看出,改进后算法的均衡器输出信号星座图明显更紧密集中、清晰,QAM信号星座点已基本不偏离原始输入星座点位置,证明改进后的算法均衡效果更好,在稳态条件下误调更小,即具有更小的剩余稳态误差。
(a)4QAM调制输入信号
3.2 均方误差比较
在与4.1节相同仿真环境下,实验仿真1 000次。对于每一次实验,均假设半盲均衡器的抽头个数为8个,根据式(16),估计均衡器初始值。通过调整不同参数值a、b,分析改进的NCMA算法收敛速度。改进后的NCMA算法的均方误差图如图6所示。
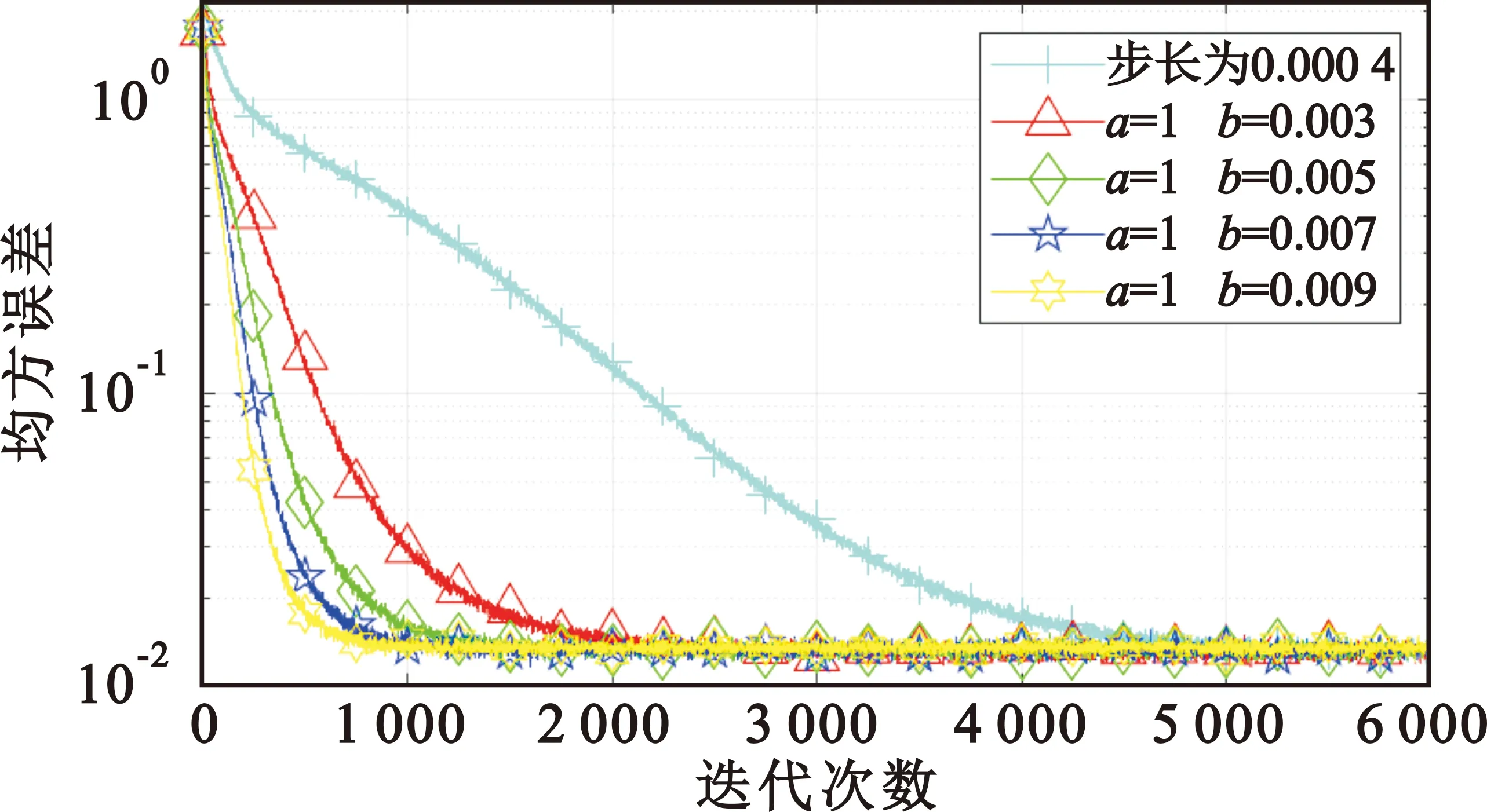
(a)均方误差vs.迭代次数(不同参数b)
由图6可以看出,给定合适范围的参数值a、b,MIMO系统半盲均衡后的均方误差随迭代次数的增加而快速减小,最后均趋于一个接近0的稳定值,此平稳值为最小均方误差。另外,与CMA算法比较,改进后的算法收敛速度明显更快。
图6(a)给定参数a=1,参数b分别为0.003、0.005、0.007和0.009。由图6(a)可以看出当给定参数a值,调整参数b值,算法的收敛速度随b值的增大而加快,当b=0.009时,算法的收敛速度最快。同时,参数b对该系统剩余稳态误差几乎无影响,剩余稳态误差相同。因此,可选取参数b=0.009作为最优均衡器的参数设定。
图6(b)给定参数b=0.009,参数a分别为0.4、0.8和1。由图6(b)可以看出当给定参数b值,调整参数a值,算法的收敛速度随着a值的增大而减慢,系统剩余稳态误差随着a值的增大而减小。当参数a取0.4时,即参数a过小时,将会明显影响系统剩余稳态误差的大小。当参数a=0.8时,该算法既可以维持较快的收敛速度,又可以保持较小的剩余稳态误差。因此,考虑到算法的收敛速度和系统的剩余稳态误差,参考图6,合理配置参数a、b的大小,可灵活实现不同步长下加快算法的收敛速度,并减小误差。
最后,在MIMO系统半盲均衡器基础上,假定CMA算法的固定步长μ=0.000 4。参考图6仿真分析,选取a=0.8、b=0.009作为最优半盲均衡器参数设定,同时运用到NCMA算法以及本文提出的改进的NCMA算法中,图7给出了这三种算法的均方误差比较图。
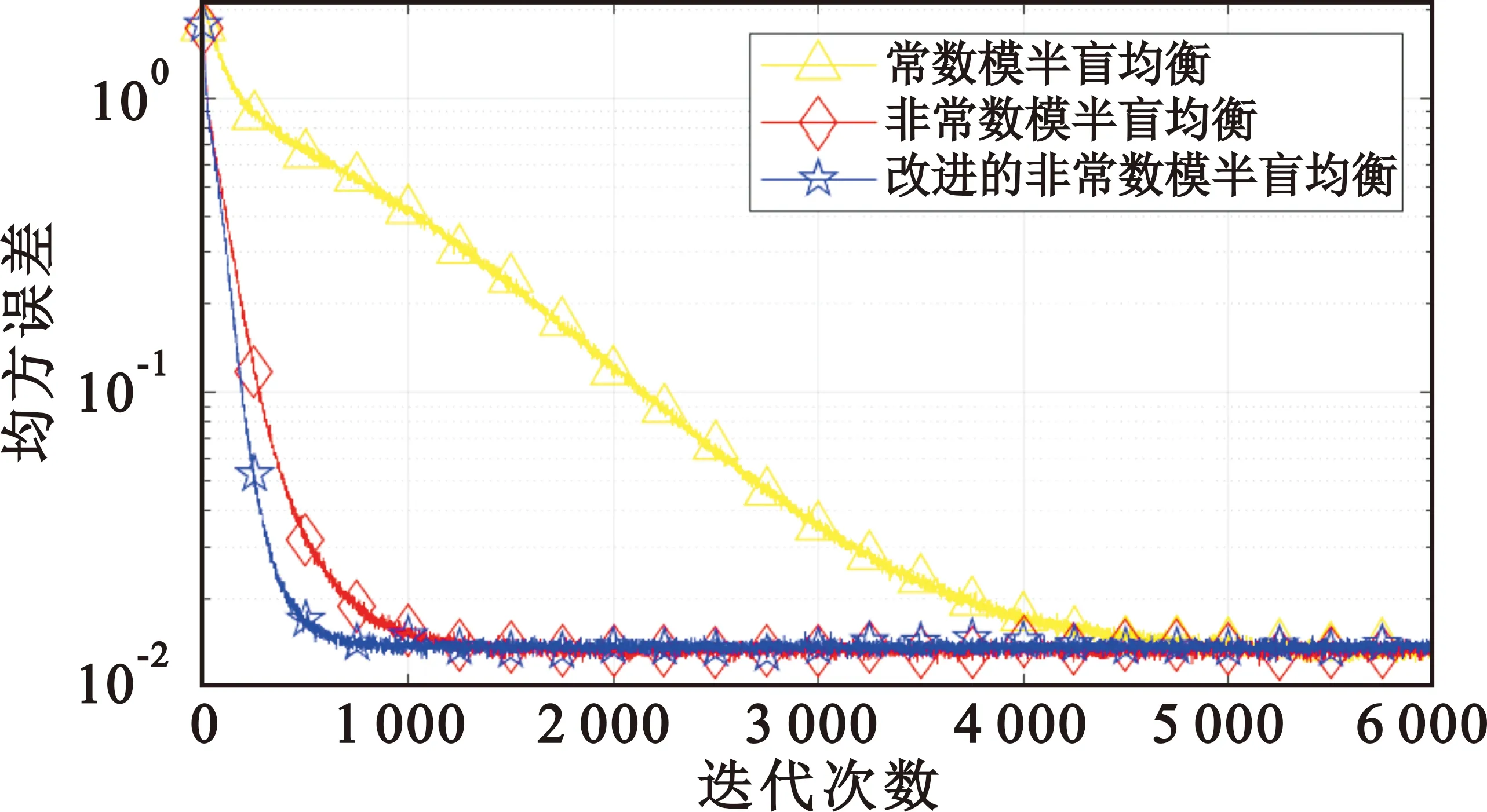
图7 三种算法的均方误差比较
由图7可以看出,CMA算法的收敛速度远远小于两种变步长算法的收敛速度。当NCMA算法以及改进的NCMA算法中参数a、b设置相同时,改进后的算法收敛速度明显更快。该算法同时能保证在算法的初始阶段也就是误差较大时,仍能保持较大的步长,加快收敛速度。
4 结束语
本文为解决MIMO通信系统传输过程中信道衰落、随机噪声、空间多径效应、共信道等问题造成接收端信号严重失真的现象,提出了一种基于MIMO信道的改进的非常数模半盲均衡方案。改进后的半盲均衡方案基于MIMO信道先验知识来估算半盲均衡器的初始值,采用变步长迭代更新均衡器权系数,寻找到最小目标函数值。相比大多数采用少量训练样本的方法设计半盲均衡器,该方案在降低计算复杂度的同时,能有效保持优良的均衡性能,且能更真实反映MIMO系统的均衡效果。
理论分析和实验仿真证明,可灵活配置多个参数调节变步长,实现在整个算法迭代过程中保持不同步长加快算法的收敛速度,并减小剩余稳态误差。同时,该算法克服了其他算法的缺点,相比之前的算法收敛速度更快,信道均衡效果更好,并且更适用于MIMO无线信道的均衡处理。另外,该方案均衡器初始值预设与MIMO信道参数有很大关联,但由于MIMO信道具有时变性、随机性,这会导致信道估计的精准性直接影响之后半盲均衡处理性能。因此,未来可进一步改进MIMO信道估计,使该算法运用到更广的领域。
——中国制药企业十佳品牌

