一种基于抽取LMS的距离旁瓣抑制方法*

鲁振兴，管吉兴，唐程远，张 焱，洪永彬，尹 伟

(1.中国电子科技集团公司第五十四研究所，石家庄 050081； 2.中国人民解放军32380部队，北京 100072)

0 引 言

噪声雷达作为现代雷达中一个新的研究领域，由于具有优异的低截获概率特性、抗干扰特性[1-2]，以及在目标参数测量方面的良好性能(如无距离、速度模糊)，近十几年来得到了快速的发展[3-4]。

在噪声雷达的相关处理中，旁瓣的抑制性能受限于处理时长与信号带宽之积，在积累增益有限的情况下会产生弱目标被发射信号泄漏、杂波以及强目标的旁瓣所淹没的现象。降低信号旁瓣最直接的方法是增大相关处理的时间，此时积累时间内目标的距离走动必须要考虑。然而，受波束驻留时间以及目标雷达散射截面(Radar Cross Section,RCS)起伏等因素的影响，相关处理时间不可能任意增大。为了在有限的处理时间之内尽量降低信号旁瓣，需要考虑一些非传统的处理方式，如CLEAN方法[5]、自适应脉冲压缩[6]、最小均方(Least Mean Square,LMS)自适应算法等[7]。

2004年，Rigling[8]将LMS类型的算法用于噪声雷达距离旁瓣抑制。直到2012年，Meller等[7]才对该类方法进行了较为详细地描述。但是，Meller的方法是基于白噪声假设的。实际系统中，为减小信号峰值损失，可能会以明显大于信号带宽的速率进行采样[9]，从而使得相邻采样点之间存在很大的相关性。此时，LMS算法的收敛速度会很慢，权系数在处理片段内可能无法收敛。虽然联合过程估计方法可以提高算法的收敛速度，但是从回归系数到距离单元的转换需要进行矩阵乘积[10]，其运算量仍然很大。

本文给出一种基于抽取LMS的距离旁瓣抑制方法，通过多个LMS滤波器并行处理，快速收敛获得低副瓣距离压缩结果。

1 LMS距离旁瓣抑制原理

假设噪声雷达回波信号中包含P个目标，其中第i个目标的延迟为ni，那么接收信号可以表示为

式中：ai为第i个目标回波信号的复幅度，Sr(n)为发射参考信号，S0(n)为接收机噪声信号。

因为目标回波可以看作Sr(n)经过一个线性滤波器之后的结果，所以可以设计一个滤波器，用参考信号经该滤波器后的输出来模拟目标回波信号，滤波器的系数就可以作为回波信号的距离压缩结果。

(1)

滤波器系数α0可以采用维纳滤波算法进行估计，但是该方法需要进行矩阵求逆，运算量很大，尤其是滤波器阶数较高时。为减小计算量，滤波器系数可以通过自适应的方式进行调整，如图1所示。实际中，由于目标回波存在一定的多普勒频率，自适应滤波可以适应目标多普勒频率的带来的系数变化。

图1 自适应LMS滤波器结构

LMS算法是一种简单的随机梯度自适应滤波算法。它不需要进行相关函数的计算，也不需要矩阵求逆，仅仅利用瞬时梯度对权向量进行调整。

假设在n时刻滤波器的权向量为α(n)，那么对梯度▽J(n)的瞬时估计为

(2)

LMS算法对加权向量的调整方法为

α(n)+μSr(n)e*(n) 。

(3)

式中：μ为迭代步长。在算法初始时刻滤波器系数α(0)可以设置为某些先验值也可以设置为0。

根据Butterweck的理论[10]，为保证LMS算法稳定，迭代步长μ的选取应该满足

(4)

式中：Smax为参考信号功率谱的最大值。

2 基于抽取LMS的距离旁瓣抑制方法

当参考信号为白噪声时，LMS算法可以具有很快的收敛速度，在处理时间内可以达到收敛状态，然而，在雷达系统中，通常会以明显大于信号带宽的速率进行采样[9]，相邻采样点之间存在很大的相关性。此时，LMS算法的收敛速度会很慢，滤波器系数在处理时间内无法收敛。因此，本文提出一种基于抽取LMS的距离旁瓣抑制方法。

对参考信号进行D倍抽取，使得抽取之后的采样频率近似等于信号带宽，这样参考信号的相邻采样点之间可以认为不相关。抽取之后的参考信号为SD(n)=Sr(nD)，以向量形式表示为

SD(n)=[SD(n),SD(n-1),…,SD(n-KD+1)]T。

(5)

式中：KD为抽取后的参考向量长度(对应抽取LMS滤波器的长度)。

同样，对接收信号也进行D倍抽取，根据初始位置的不同，可以得到D个不同的信号，其中第m个信号为

xD,m(n)=x(nD-m)。

(6)

式中：m=0,1,…,D-1。

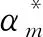
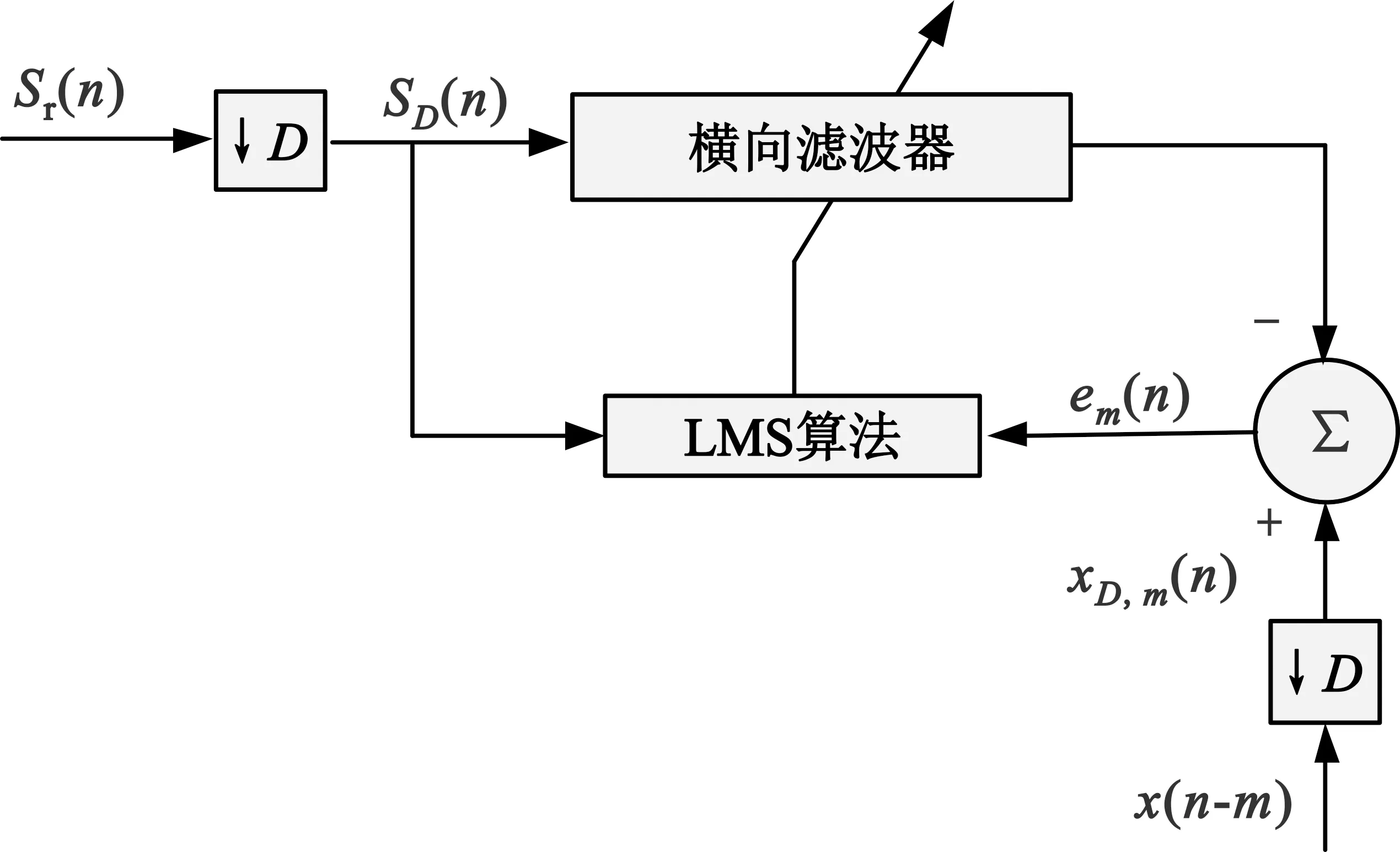
图2 抽取LMS滤波的原理

由于接收信号被抽取成了D个不同的信号，因此可以得到D个与图2结构相同的LMS滤波器。相应地，第m个LMS滤波器的权系数更新方法为

(7)

式中：

最终，得到KDD个距离单元的距离像为

α*(n)=[α1,1(n),α2,1(n),…,αD,1(n),α1,2(n),

α2,2(n),…,αD,KD(n)]H。

(8)

3 性能分析

因为参考信号SD(n)的相关矩阵近似为单位阵，第m个LMS滤波器系数αm(n)的收敛过程与自然模式相同[10]。假设最优滤波器的权系数向量为αm，那么在小步长条件下，vm(n)=αm-αm(n)的第i个元素的均方收敛过程为

(9)

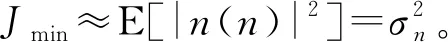
对于单位幅度的噪声调频信号，λi≈E[|SD(n)|2]≈1(实际系统中对接收参考信号进行滤波后信号幅度会有轻微的损失)，所以，算法收敛后第i个权系数的方差为

(10)

假设αm中的非零值只有αm,i，那么输出结果的峰值旁瓣比(Peak Side Lobe Ratio,PSLR)为

(11)

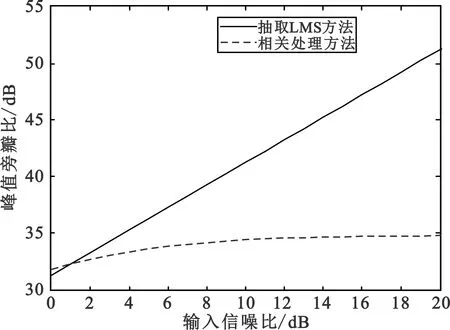
图3 PSLR随输入信噪比的变化(BT=35 dB，μ=1.5×10-3)

4 仿真分析

4.1 距离像的仿真分析

仿真中采用带宽10 MHz、采样率30 MHz的噪声调频信号。不过为了使抽取后的信号满足采样定理，使参考信号和接收信号在进入抽取LMS滤波器之前经过带宽为9.8 MHz的低通滤波器，以滤除边带成分。算法中令抽取倍数D=3，滤波器长度KD=300，步长参数μ=1.5×10-3。

假设两个目标的延迟分别为100和500个距离单元，功率比为30 dB，弱目标信噪比为0 dB。在处理时长为300 μs的情况下，图4给出了相关处理算法、抽取LMS算法以及LMS算法得到的距离像，其中后两种算法的距离像初始值(迭代初值)均为0，LMS算法中滤波器长度为900，步长参数与抽取LMS算法相同。由于此时的相关处理增益仅为35 dB，弱目标的相关峰值仅比强目标的噪声基底大5 dB，所以在图4(a)中，弱目标无法被检测出。而LMS方法的收敛速度很慢，在300 μs的处理时间内远没有达到收敛状态，此时在图4(c)中弱目标也无法被检测。在抽取LMS算法中，距离像的噪声基底明显降低，弱目标可以被检测。但是，由于之前对信号进行了滤波处理(滤波器频域响应近似为矩形)，算法输出的距离像旁瓣较高。此时通过对输出距离像进行“频域加窗”处理(通过时域卷积实现)[7]，可以使距离旁瓣明显降低。通过汉宁窗处理之后，得到的距离压缩结果如图4(d)所示。

(a)传统相关处理

图5给出了当强目标的距离延迟为100.5个采样点时，抽取LMS算法得到的(加窗处理后的)距离压缩结果，可以看出目标的分数延迟对算法性能并没有太大影响。

图5 分数延迟情况下抽取LMS算法得到的距离压缩结果

4.2 弱目标检测概率的仿真分析

假设强目标和弱目标的幅度分别为a1和a2，延迟分别为τ1和τ2(仍假设τ2=500Δt)。在不同信噪比及强目标延迟情况下，图6 给出了小目标检测概率随两目标回波功率比的变化，其中检测门限按照虚警概率Pfa=1.2×10-4进行设置。由图6也可以看出，当信噪比较大时，抽取LMS算法的性能要明显优于传统相关处理方法；而在0 dB信噪比下，抽取LMS算法与相关处理方法性能基本相同。图6中抽取LMS算法相对于相关处理方法的性能改善大小与图3给出的理论结果基本一致。另外，可以看出目标的分数延迟对算法性能的影响很小。

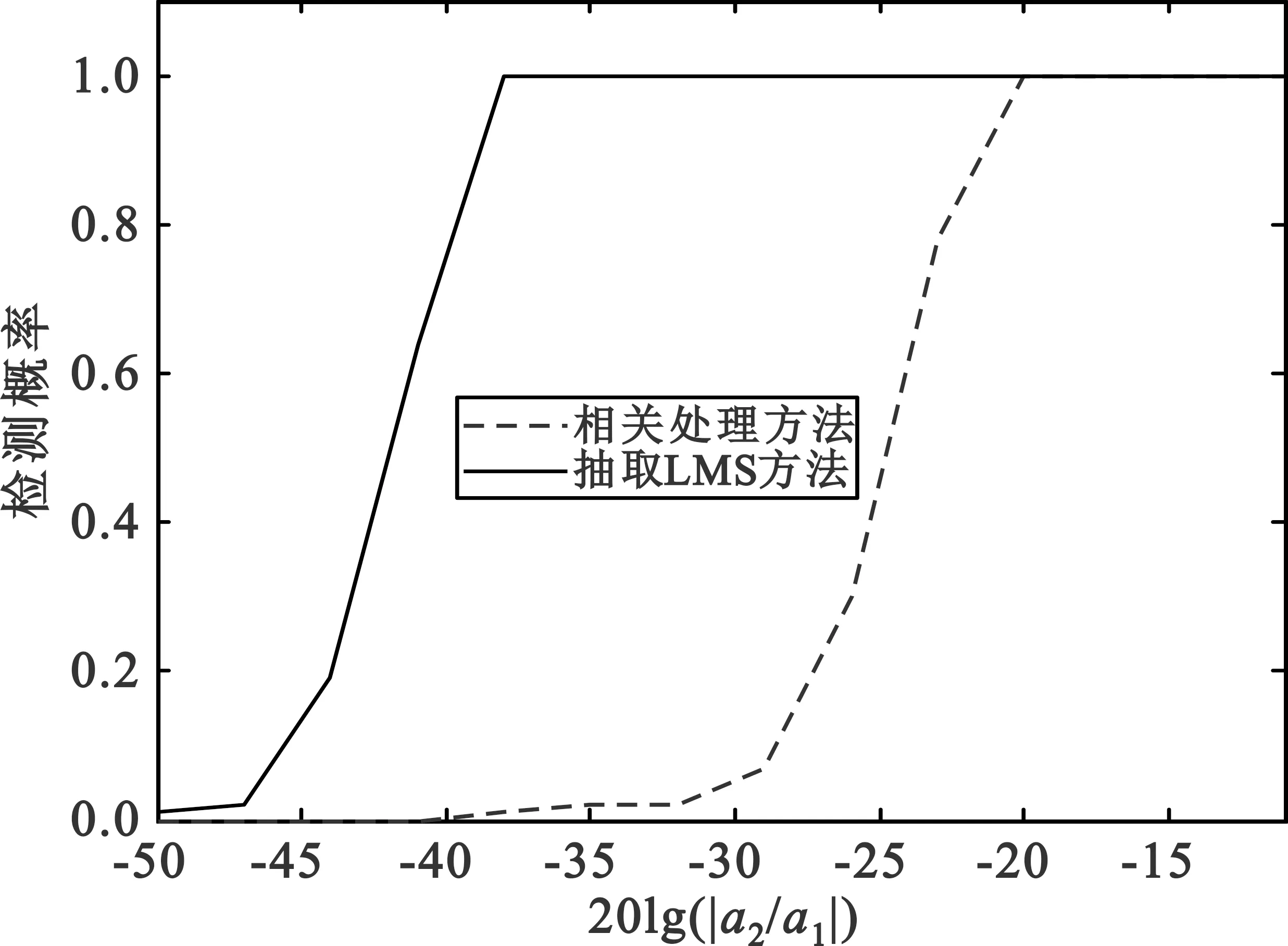
(a)SNR1=20 dB，τ1=100Δt

4.3 峰值旁瓣比随输入信噪比的变化

假设回波中仅存在一个目标，目标位于第50个距离单元，步长μ=3×10-3，其他参数不变，此时通过仿真得到峰值旁瓣比随目标信噪比的变化如图7所示。可以看出，该方法得到的峰值旁瓣比随输入信噪比的提高而增大，并且仿真结果与理论分析一致。

图7 抽取LMS算法PSLR随信噪比的变化(μ=3×10-3)

5 结 论

本文针对噪声雷达回波信号相关处理中存在的距离旁瓣较高的问题，提出了一种基于抽取LMS的距离旁瓣抑制方法，通过多组抽取LMS滤波器计算距离压缩结果。对算法的性能进行了理论分析，得到的PSLR正比于输入信噪比，而不受信号时宽带宽积的限制。通过数字仿真对算法的性能进行了验证，与传统的相关处理方法相比，所提方法可以明显提高距离旁瓣抑制能力，并且PSLR与理论分析一致。