利用HHT-EEMD方法分析云南区域GNSS应变时序孕震信息

高 涵,袁希平,甘 淑,张 明

1. 昆明理工大学国土资源工程学院，云南 昆明 650093； 2. 云南省地震局信息中心，云南 昆明 650225； 3. 云南省测绘产品检测站，云南 昆明 650034

由于具备全天候、高精度、三维定位的优势，GNSS连续观测技术的应用已逐渐由传统空间大地测量学领域向地球物理学学科过渡，被地震学家广泛应用于地壳运动监测当中，逐渐成为地震地壳监测不可或缺的补充手段[1-9]。伴随现代信息技术的发展，人们不再将地震活动当成瞬时状态改变，而更加倾向于通过地壳活动的历史规律及动态运动过程来理解地震孕育活动。

国内外众多学者通过地表监测时间序列的方法对地震活动进行了深入研究。文献[10]通过电磁观测网在云南漾濞地震前夕从电磁时间序列中得到了地震前兆信息。文献[11]通过Swarm卫星建立了一种从卫星地磁时间序列测量中检测异常并进行地震预报的分析方法，通过研究得出高质量的长期观测数据是确认与地震或其他自然灾害有关的异常的必要条件。文献[12]通过综合检校法考虑同震阶跃和RMS减小率，判断可疑站点是否受地震影响,识别和估计了时间序列中的同震和震后形变。文献[13]通过ARMA方法利用GPS时间序列对尼泊尔地壳形变和应变进行了测量和建模分析，研究发现从尼泊尔北部到南部边界的8～10 mm/a的主推力是该区域构造应变变化的主要原因。文献[14]通过相对强度指数自动探测了单站GPS时间序列中的瞬间变形，验证了该方法是一种能够从地球物理位移时间序列中自动检测异常的稳定客观的方法。然而，相对于地表位移时间序列，较少有学者专注于应变时序历史信息研究，通过云南省地震局的相关研究发现[15]，GNSS应变反映的变化过程可能与强震的孕育-发生之间存在联系，应变及其异常变化的研究对未来强震危险区的判识具有重要意义。然而传统的时频分析方法中傅里叶变换是一种全局的变换，不在时域即在频域，无法表述信号的时频局部性质，而时频局部性质恰好是非平稳信号最基本和最关键的性质。传统的小波变换虽然具有自动改变窗口长短的功能，可以较好地把信号在时间上和频域上局部化，从而呈现了信号的局部奇异性，但选择小波基困难，小波基不能对信号进行自适应。

综上所述，为了深入挖掘应变时序中所携带的信号特征，本文针对应变时序选取专门适用于非线性非平稳信号处理，又克服了传统傅里叶变换和小波变换缺点的时频分析方法，即整体经验模态分解的希尔伯特-黄变换分析方法(Hilbert-Huang transform-ensemble empirical mode decomposition，HHT-EEMD)来探索云南区域中强地震前GNSS应变时序中的时间-频率-能量联合分布特征，尝试挖掘应变时频信号中所携带的孕震信息，为未来云南区域强震的判定提供一定的参考。

1 HHT-EEMD数学模型

希尔伯特-黄变换(HHT)[16-18]主要包含2个步骤：经验模态分解(empirical mode decomposition,EMD)与Hilbert谱分析(Hilbert spectral analysis,HSA)。首先，EMD可以自适应地将原始信号分解为频率由高至低的固有模态分量(intrinsic mode functions,IMF)和一个残差趋势项，分解得到的IMF分量具有一定的物理意义；其次，再对各个IMF分量进行Hilbert变换，获得其对应的瞬时振幅和瞬时频率，进而把瞬时振幅表示在时频表面上，就得到了Hilbert谱，这一过程称为希尔伯特-黄变换，即HHT。

同时需要指出的是，EMD方法容易产生模式混叠现象，造成边界效应，而整体经验模态分解(ensemble empirical mode decomposition,EEMD)可利用随机噪声削弱这种现象[19-20]。因此，本文采用EEMD方法来将原始信号分解成IMF。

1.1 EEMD

EMD的原理是首先搜索原始信号s(t)所有的极大值点与极小值点，然后将所有极大值点和所有极小值点分别用一条曲线拟合得到s(t)上、下包络线；若上、下包络线的均值记作m(t)，用s(t)减去m(t)得到的新序列记作ci(t)，若ci(t)满足一定的条件时，定义ci(t)为IMF的一个分量，否则视ci(t)为新的s(t)继续重复以上操作，直至ci(t)满足要求为止。由此可分解得到n个IMF分量和一个残差趋势项，即

(1)

式中，ci(t)为第i个IMF分量；rn(t)为残余趋势项。

而EEMD就是在进行每一次EMD分解之前，在原始信号s(t)中加入一定量的高斯白噪声wk(t)，第k次待分解的信号表示为

sk(t)=s(t)+wk(t)

(2)

由于高斯白噪声是一个均值为零的正态随机序列，因此当达到一定重复分解次数时，即可消除加入的白噪声影响，使得分解后的IMF均来自s(t)本身。

利用EEMD可以实现原始时间序列中噪声的分离，EEMD是将组成原始信号的各尺度分量不断从高频到低频进行提取，则分解得到的IMF顺序是按频率由高到低进行排列的，即首先得到最高频的分量，然后是次高频的，最终得到一个频率接近为0的低频残余分量。在地震监测时间序列分析中，高频信息频率较高代表噪声、误差等短周期抖动；低频IMF分量相对高频分量较为平缓，主要代表区域地壳中长趋势运动特征。

1.2 Hilbert谱分析

对给定的连续曲线X(t)，其Hilbert变换定义为

(3)

式中，PV表示奇异积分的主值；τ为平行移动窗口参数。通过Hilbert变换，解析信号定义为

Z(t)=X(t)+iY(t)=a(t)ei θ(t)

(4)

(5)

(6)

式中，a(t)是瞬时振幅；θ是相位函数；瞬时频率ω(t)可表示为

(7)

在得到IMF分量后，很容易将Hilbert变换应用于每个IMF分量，然后根据式(3)—式(7)计算瞬时频率。对每个IMF分量X(t)执行Hilbert变换后，H(ω,t)可以表示为

(8)

式中，Re[•]表示“•”的实部；aj(t)和ωj(t)分别是第j个IMF的瞬时振幅和频率。振幅的频率-时间分布称为“Hilbert振幅谱”H(ω,t)，或者简称为“Hilbert谱”。定义Hilbert谱后，进而可以将边际谱H(ω)定义为

(9)

2 数据处理及分析思路

本文选取了包括陆态网络及云南省地震局自建站在内的云南区域59个GNSS连续跟踪站2013—2019年所观测到的30 s采样间隔的观测数据，首先利用GAMIT软件进行基线解算，获得测站的区域单日松弛解；然后通过GLOBK软件将区域单日松弛解和SOPAC提供的IGS全球单天无约束解联合平差，得到ITRF2014框架下的测站4日解坐标时间序列，进而获取得到区域GNSS位移场；最后，将研究区域(97°E—107°E，21°N—29°N)进行1°×1°格网化，用网格化后的格网最终代表该格网经纬度范围内的应变情况，并按照从S至N，W至E的顺序进行编号，如图1所示。其中，震源球表示研究区域内2013—2019年Ms≥5级地震的震源机制解。

图1 网格划分及站点分布[21]Fig.1 Grid division and site distribution[21]

划分格网后，参考文献[22—23]中的平面应变计算公式以计算不同格网的应变分量。首先需要通过Kriging插值方法对区域内分布不均匀的站点位移进行插值，得到不同格网的位移数据，进而通过应变计算得到80个格网的应变参数时间序列，部分应变时间序列如图2所示。其中，黑色竖线标注为格网时间点对应的地震。由于地震活动是大气-陆地相互作用、海洋-陆地相互作用、人类-地面相互作用、地球内部之间相互作用、火山活动等因素共同作用的结果，这必然导致地震观测中存在各种杂乱无章的噪声信号。如图2所示，由于应变时间序列中包含了各类噪声干扰，有可能掩盖地震前的异常信号。因此，在分别获取得到80个格网的应变时间序列后，还需利用适用于非线性非平稳信号处理的HHT-EEMD分析方法对结果进行分析去噪，进一步尝试挖掘孕震信息。

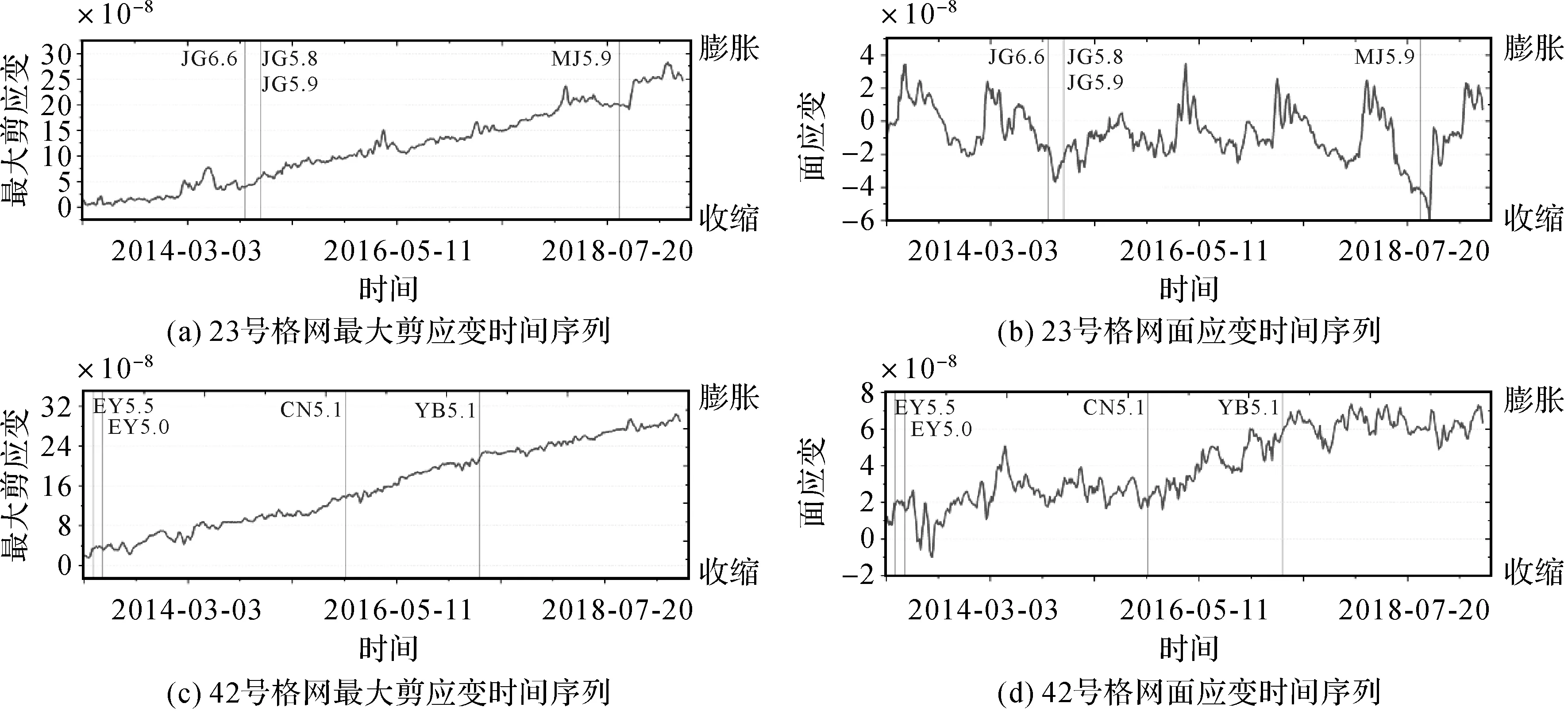
图2 格网应变时间序列Fig.2 Strain time series of grid

HHT-EEMD分析思路如下。

(1) 对每个格网应变时间序列进行EEMD分解，将应变时序分解为不同频率的IMF分量和残差趋势项。

(2) 残差趋势项分析：残差趋势项主要代表格网长周期运动趋势，对部分典型格网及周边格网进行联合分析，可判断格网与周边格网应力状态、张压特性等，进而初步从宏观了解格网区域内应变积累态势。

(3) IMF分量异常曲线识别：通过显著性检验从不同频率的IMF分量中选取出包含有效信息的IMF分量，再划定2倍标准差曲线作为选取的IMF分量的异常指标阈值，超过即视为异常。

(4) 进一步对选取的IMF分量进行Hilbert变换，获取该分量的时间-频率-振幅联合分布特征(Hilbert谱)，以及瞬时频率、瞬时振幅等局部特征(Hilbert瞬时能量谱)。

(5) 联合云南区域的历史震例，结合上述HHT—EEMD分析结果进行震例总结，从应力、构造活动等方面对格网内历史地震进行分析，尝试挖掘应变时频信号中所携带的潜在信息。分析流程如图3所示。

图3 处理及分析思路Fig.3 Processing and analysis ideas

3 结果分析与讨论

3.1 残差趋势项分析

如前所述，首先对获取得到的80个格网应变时间序列进行EEMD分解，得到与之对应的IMF分量和残差趋势项，残差趋势项如图4所示。图中每个格网的x方向代表时间，y方向代表格网应变时序对应进行EEMD分解后得到的长周期残差趋势项。由图4可以发现，残差趋势项消除了高频IMF分量噪声的影响，体现了原应变时间序列的总体运动趋势。对格网及周边格网进行残差趋势项联合分析，可以判断格网相对于周边格网应力状态、张压特性等特征随时间的相对变化趋势，进而对比发现并找出格网间的差异性运动，从宏观角度了解区域应变相对积累态势。不同格网应变-时间分析方法与传统的静态应变相比，具有丰富时间维度信息，突出应变变化细节的优势。

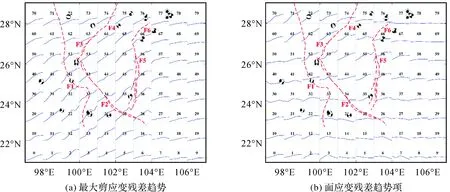
图4 2013—2019年网格应变时序经EEMD分解后的残差趋势项Fig.4 Residual trend term of each grid stain time series after decomposition by EEMD during 2013—2019

由图4最大剪应变残差趋势项可以发现，除靠近东部区域华南板块的格网以外，云南区域剪应变运动整体活跃，小江断裂带(F5)、莲峰断裂(F6)相关格网为整个云南的剪应变相对高值区，与云南区域其他格网相比，该断裂带区域剪切运动更为突出，这与历史上这一断裂带周边频发走滑性质强震的现象相符。另外，澜沧江断裂(F1)北段呈显著面应变高值，而南段剪应变呈现出相对高值，说明这个区域的剪切运动较为活跃，这与澜沧江断裂带在新生代强烈活动,且以走滑逆冲运动为主相符。这可能是在太平洋板块向西推挤作用下的扬子华南板块与印度板块发生强烈碰撞挤压、向北运移，在北部强烈挤压，在南部强烈运移共同作用的产物。同时，结合图1和表1整理收集的云南区域2013—2019年Ms≥5级的历史震例震源机制解信息来看，该区域的剪应变活动高值异常与统计年间区域内地震活动活跃较为相符。

由图4面应变残差趋势项可以看到，以红河断裂(F2)为界，北部面膨胀活动较为活跃，川滇菱形块体西北部拉张明显，由西向东逐渐由张转压，整个云南区域主要呈现张压交替的时空演化特征，这种现象表明红河断裂在云南区域的面膨胀构造运动中起重要作用。鹤庆-洱源断裂(F3)、小金河断裂(F4)附近，面应变伴随时间的推移而展现出局部相对高值的运动趋势，由表1可知，云南区域内地震活动主要以走滑断层破裂为主，而该区域统计期间却于2013年发生了正断型断层破裂的Ms5.9德钦地震，这种发震断层活动性质与区域格网运动相符的现象表明地震孕育活动与区域内剪应力和张压应力伴随时间发展的相对运动趋势高度相关。

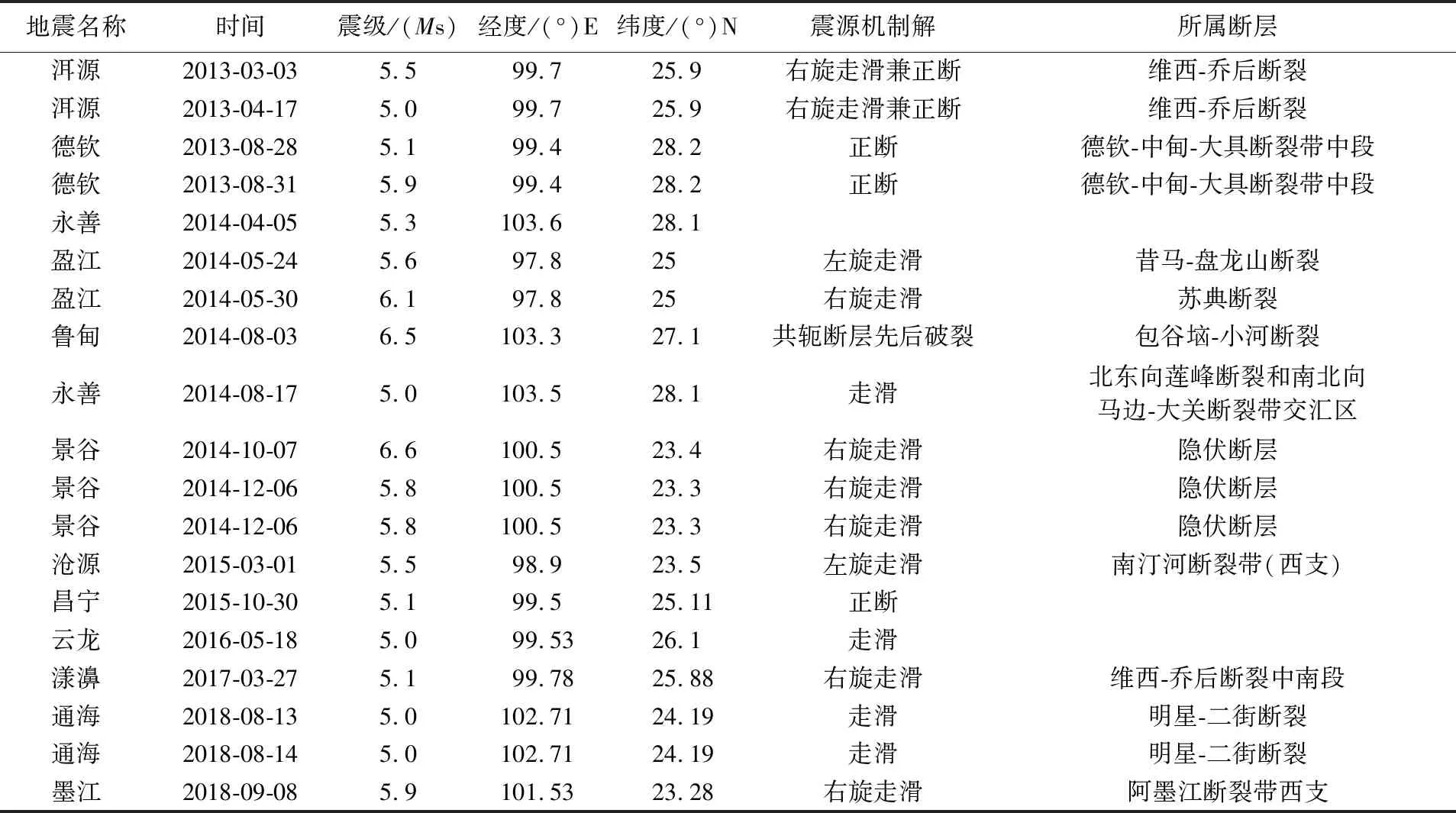
表1 云南区域Ms≥5.0级地震统计表(2013—2019年)Tab.1 Earthquake statistical table above Ms5.0 in Yunnan region(2013—2019)

3.2 震例总结

前文虽然基于EEMD分解的应变时序残差趋势项从宏观角度分析了云南区域长趋势应变积累态势，但无法获取应变信号中所包含的瞬时活动特性，因此下文将进一步结合HHT分析方法，通过显著性检验选取出较为合适的IMF分量进行Hilbert变换，获得其时间-频率-振幅(能量)的联合分布特征(Hilbert谱)，以及瞬时频率和瞬时振幅等局部特征(Hilbert瞬时能量谱)，并结合区域构造信息对部分格网进行震例总结，尝试挖掘应变时序时频信号中所携带的孕震信息。

3.2.1 震例1: 23号格网对应地震

23号格网内，分别发生了2014年10月7日景谷Ms6.6级，以及12月7日景谷Ms5.8、Ms5.9级地震，震中均位于云南省普洱市景谷傣族彝族自治县。另外，2018年9月8日的墨江Ms5.9级地震震中在云南普洱市墨江县，位于23号格网右侧相邻的24号格网。由图4的面应变残差趋势图可以看到，该区域的面应变活动稍有压性但整体较为平缓，而剪应变活动较为剧烈，甚至较少有衰减现象，这说明该区域内的走滑断裂中长期处于活跃状态，其构造应力主要受剪应力支配。区域内剪应变变化活跃、面应变变化平缓的应变特性与景谷地震发震于右旋走滑的隐伏断层和墨江地震发震于右旋走滑的阿墨江断裂带西支断裂的现象相符，这从断裂活动特性与断层调查性质一致的角度验证了本文中应变残差趋势分析的适用性。

图5(a)和图6(a)分别是23号格网最大剪应变时序和面应变时序进行EEMD分解后的8个IMF分量结果。可以看到，IMF的各个分量按照从高频到低频的顺序依次排列，高频IMF频率较高代表噪声、误差等短周期抖动，残差趋势项代表区域地壳中长趋势背景运动特征，可见EEMD具有分频剖面的类似特征，可以利用信号与噪声在不同固有模态函数剖面上的差异来去噪，分离高频噪声和低频趋势，进而突出异常信号特征。

获得IMF分量之后，再对其进行显著性检验选出包含有效信息较多的IMF分量，如图7所示。由文献[24]可知，IMF分量于置信曲线上且越远离置信区间曲线，说明IMF中所携带的有用信息越多。从最大剪应变显著性检验图中可以看出，IMF5和IMF6分量相对其他分量距离回归曲线较远；而从面应变显著性检验图中可以看出，IMF5分量相对其他分量距离回归曲线较远，因此，笔者认为这些中低频的IMF分量中可能存在有用信息，下面将尝试从上述IMF分量中提取异常信息。震例2的IMF分量选取方法同上，后续不再赘述。

图7 23号格网最大剪应变和面应变的IMF分量显著性假设检验Fig.7 The significance of dilation strain and maximum shear strain IMFs for No. 23 grid cell

选定IMF分量后，首先对其进行异常曲线识别。由于地块并非“完美”刚性块体，受外部作用力后，块体的运动状态将以应力强弱的形式表现出来，如果通过块体的历史应变状态建立线性回归模型，则当块体本身的变形或状态异常时，必定会与原有的回归模型产生较大的偏差，统计后发现去趋势后的应变值服从正态分布，95%以上的数据均在2倍标准差之内[22-23,25]，因此，本文以2倍中误差为限设置异常指标线，超出2倍中误差则认为块体运动异常。而在计算2倍中误差过程中，常规的统计方法不考虑数据的预测时间节点，是一种依赖时间的未来函数，本文采用对时间逐渐累积，数据逐渐参与计算的方法，来进行异常指标线获取，即对于历史信息T日只用T-1日前的数据参与计算，划定2倍标准差作为异常指标阈值，最终获得不依赖于T+1日后的数据得到的异常指标曲线。选定的IMF分量及其异常指标曲线如图5(b)、(c)和图6(b)所示。

图5 23号格网最大剪应变时间序列HHT-EEMD结果Fig.5 The maximum shear strain HHT-EEMD results for the No. 23 grid cell

然后，对选定的IMF分量进行Hilbert变换，以获得瞬时频率、瞬时振幅等局部时频信息，图5(d)和图6(c)是最大剪应变时序和面应变时序分别对应的总Hilbert谱。图5(e)—图5(h)和图6(d)、图6(e)是选定的IMF分量经Hilbert变换获取的Hilbert谱、瞬时振幅与瞬时频率。从整体来看，剔除了高频噪声和低频趋势后的中频应变IMF曲线，无论是最大剪应变还是面应变均在景谷两次地震和墨江地震前夕出现异常波动，均超过了图中的2倍标准差曲线，且均呈现出瞬时振幅突然增大的现象，这可能与当前IMF分量频率对应的地壳复杂运动和地壳震前地震能量的早期释放有关。同时，也表明HHT-EEMD在地震信号分析中具有较好的描述信号局部时-频特性的能力，能够一定程度描述应变时序的时变特性，具有较高的时间和频率分辨率。假设选定IMF中地震前夕瞬时能量的突然增加是有效地震信号的前提下，由图5(f)、(h)和图6(e)可知，包含信号的IMF会长时间处于正常波动状态，并且只会在地震发生前不久产生异常。上述现象从时频分析的角度解释了为什么只能找到地震所属板块的运动趋势，而较早进行地震预测非常困难。在地震发生前的较短时间内虽然可能会有异常扰动信号但如果要在地震前有效地挖掘到孕震信息，则相关信号时间序列的计算周期必须小于地震信号出现的时间。另外，格网最大剪应变的异常比面应变突出，这也与景谷地震以及墨江地震发震于右旋走滑断裂的性质相符。

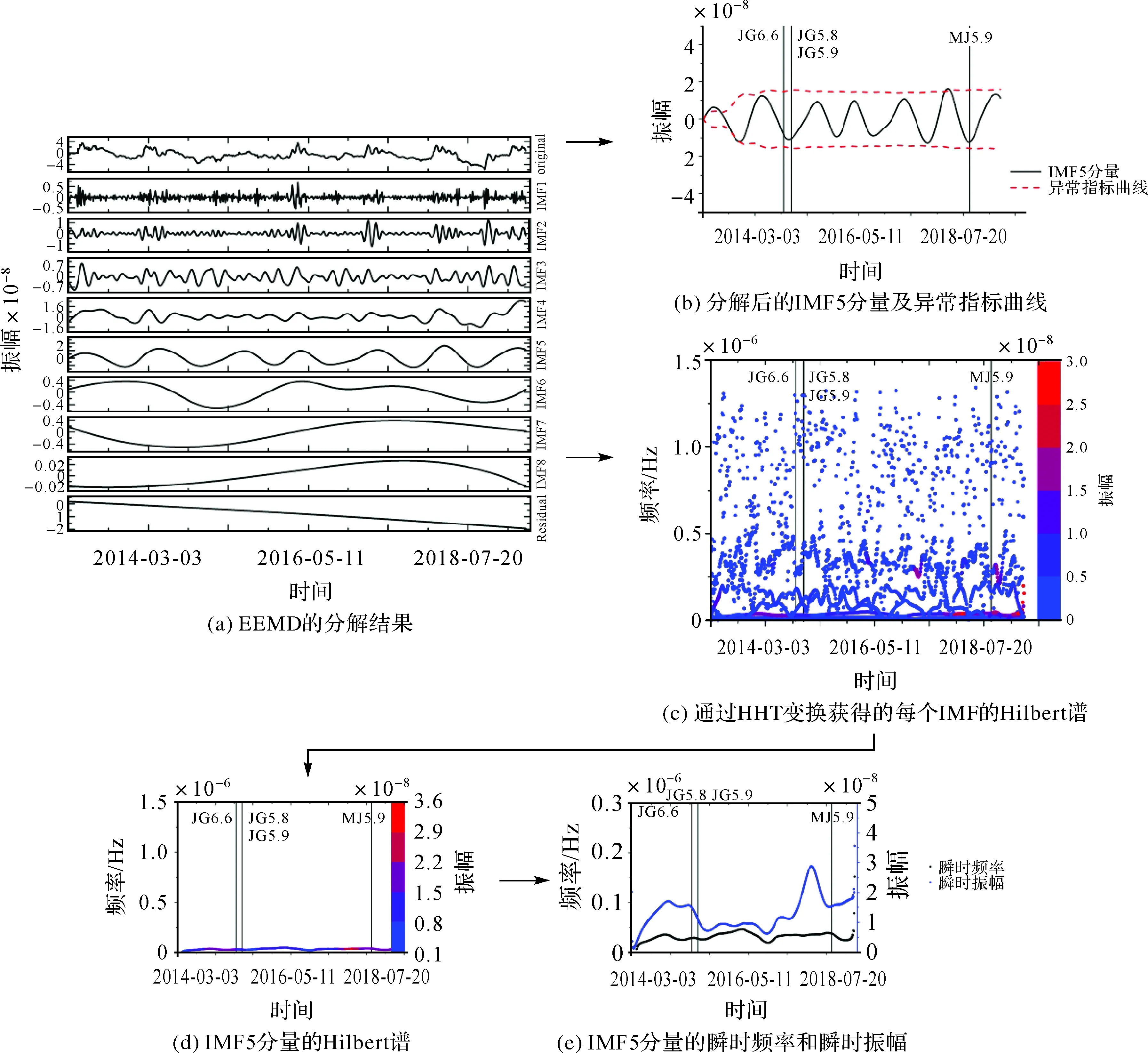
图6 23号格网面应变时间序列HHT-EEMD结果Fig.6 The dilation HHT-EEMD results for No. 23 grid cell

3.2.2 震例2： 42号格网对应地震

42号格网内，发生了2013年3月3日、4月17日的洱源Ms5.5、Ms5.0级地震，2015年10月30日的昌宁Ms5.1级地震，以及2017年3月27日漾濞Ms5.1级地震。洱源地震发震于右旋走滑兼正断性质的维西-乔后断裂；通过震源机制解评估昌宁地震可能发震于42号格网内的正断性质隐伏断裂；漾濞地震发震于右旋走滑性质的维西-乔后断裂中南段。

图8和图9分别是42号格网最大剪应变时序和面应变时序HHT-EEMD的结果。可以看出，虽然最大剪应变的IMF5、面应变的IMF4也出现了在地震前瞬时振幅突然增大的现象，但与震例1中不同的是：在42号格网内敏感IMF分量并未出现超过2倍标准差现象，但敏感IMF在经过Hilbert变换后，却在地震前呈现出一定的异常信号，这表明Hilbert变换能够有效地将信号分解在时频维度，在IMF分量异常曲线识别无效的情况下，仍然能够更深层次地通过局部的瞬时频率、瞬时振幅等方式凸显异常，对于应变时序的异常识别具有一定的适用性。

图8 42号格网最大剪应变时间序列HHT-EEMD结果Fig.8 The maximum shear strain HHT-EEMD results for the No. 42 grid cell

从震例结果来看，经过EEMD分解后的每个IMF分量代表了原始信号相互独立的各频率分量，其能将原始应变时间序列中的不同频率信号清晰地剥离，揭示信号里蕴含的高频、中频和低频等多尺度振荡特征。EEMD分解得到的IMF分量中：高频分量可能主要由各种噪声组成，因此离散度高。中频分量可能包含一定的前兆信息，但其中常伴有季节性、年变等周期扰动。当判断中频IMF分量显著性时，可通过显著性检验方法选取包含较多信息的IMF分量后，再进一步对其进行异常曲线识别和判断，以及Hilbert变换，可获得信号的瞬时频率、瞬时振幅等局部特征，进而更深层次地凸显信号中所含的异常信息，为中强地震的判定提供一定的参考辅助。低频IMF分量则多代表信号的长周期趋势性变化。EEMD算法虽然是一种完备性好，对平稳信号、非平稳信号、非线性信号都适用的自适应的信号处理方法，其与EMD相比，能在一定程度上克服模态混叠现象，但该方法添加的白噪声残留可能给信号带来噪声干扰，如图8(e)中震后峰值、图9(e)中的第二高峰值。虽然白噪声有助于削弱模态混叠现象，但在信号中引起了噪声残留，因此当异常信号出现时，需要多种异常判据进行相互佐证，综合判断异常指标曲线、瞬时频率和瞬时振幅的共振程度，是否有关的异常判据均处于极值、拐点或其他态势，并通过不断积累数据建立信号回归经验方程以不断提高孕震分析的可靠性。此外，分解得到的IMF分量偶尔会存在上、下包络在数据序列两端发散的现象，且这种发散会随着运算的进行而逐渐向内，从而使得整个数据序列受到影响，造成信号的端点效应。端点效应是影响EEMD分解精度的主要因素，如图5(b)MJ5.9后面的峰值信息，在靠近结束边缘区域出现了非常大的抖动。当遇到端点异常信号时，不能完全确定端点处的异常信号是有效信号，需要进一步通过镜像法、极值延拓法、神经网络预测、多项式外延方法、平行延拓法、边界局部特征尺度延拓法等算法来削弱抑制端点效应，综合分析区域内其他地震地质相关资料，利用除此IMF分量外的其他异常因素来推测其发震的可能性。

图9 42号格网面应变时间序列HHT-EEMD结果Fig.9 The dilation HHT-EEMD results for No.42 grid cell

4 结 语

本文基于云南区域2013—2019年GNSS格网应变时间序列，利用HHT-EEMD分析方法，结合震例探索云南区域中强地震前GNSS应变时序的时-频-能量分布特征，研究其作为孕震信息的有效性。结果显示：

(1) EEMD可依据数据的时间特征尺度进行分解，将不同频率的信号依次剥离，能有效分离高频噪声和低频趋势，较好地剖析地震信号在不同频率尺度上的变化特征。

(2) 通过绘制、对比不同格网的残差趋势项，能够发现不同格网间随时间变化的相对应变差异运动趋势，与传统的静态应变图像相比，残差趋势项图丰富了时间维度信息。

(3) 通过显著性检验选取包含信息较多的IMF分量，并对其进行Hilbert变换，可获得瞬时频率、瞬时振幅等局部时频信息。在地震前，选取的IMF分量瞬时振幅突然增大的现象可能与当前IMF分量频率对应的地壳复杂运动和地壳震前地震能量的早期释放有关。

(4) Hilbert变换能够通过信号的瞬时局部特性描述信号随时间的细微变化，在异常曲线识别无效的情况下仍能更深层次凸显异常，对于时序的异常识别具有一定的适用性。

(5) 通过EEMD、残差趋势项分析、IMF分量异常识别和Hilbert变换的方法综合动态分析应变时间序列，能够在部分地震前夕发现一些潜在异常信息，为未来云南区域强震危险地点的判定提供一定的参考，对于未来更加科学地挖掘应变时序中蕴含的孕震信息有一定探索意义。

致谢：感谢云南省地震局信息中心提供的数据支撑；感谢云南地震台洪敏老师给予的支持与帮助。