基于改进RRT 算法的移动机器人路径规划方法*

赵文龙 Abdou Yahouza M.Sani

（上海工程技术大学机械与汽车工程学院 上海 201620）

1 引言

全局路径规划算法主要有基于图搜索的Dijkstra、A*、D*算法以及基于采样的PRM、RRT、RRT*等算法［5］。相比于常用的A*等算法，基于采样的路径规划算法在高维及大尺度的环境下具有显著的优势，此外其还考虑了机器人的非完整性约束，因此对该类算法的研究非常有必要。LaValle 等提出的快速随机扩展树法（RRT）［6～7］，是一种概率完备的算法，但规划的路径不是最优的。为了解决RRT算法所规划的路径不最优的问题，文献［8］中，Karaman Sertac等提出了RRT*算法，其改进了RRT算法的父节点选择机制，并增加了重布线机制。这使得RRT*算法能渐进收敛到最优路径，但改进的方法为了优化路径而增加了耗时。文献［9］提出的informed RRT*算法引入了一个启发式的椭圆采样区域，通过在椭圆区域里不断采样使路径逐渐趋于优化，由于限制了采样区域从而减少了无效采样，提高了算法的效率。为了平滑路径，文献［10］中，Webb D J 等提出的Kinodynamic RRT*算法将机器人的动力学约束考虑在内，通过改变转向函数以适应机器人导航中的运动或其他约束。文献［11］引入了一种Dubins 路径用来做平滑优化，但是由于是直线和圆弧拼接产生的路径，因此路径曲率不连续。文献［12］中杜明博等结合环境约束和车辆约束，引入了合理的度量函数并提出一种最大曲率约束的后处理方法使规划的路径平滑可行。为了简化随机树的结构，文献［13］中，谭建豪等提出一种改进的RRT*FN 算法，其采用启发式采样的方法，并对树中的叶子结点采用加权删除法以减少内存消耗，同时提升算法性能。为了选择合适的度量函数，文献［14］中，Faust提出利用偏好评估的强化学习，提高机器人学习效率，在复杂的环境下使得移动机器人快速规划出可行路径。文献［15］中，徐娜等将移动机器人的非完整约束条件与RRT 搜索算法相结合，以解决受动力学约束的移动机器人运动规划问题。文献［16］中，刘成菊等提出以一定概率选择目标点、增加引力分量以及路径平滑处理等方式改进的RRT 算法，将其应用于nao 机器人在动态移动障碍环境下的路径规划。

相较于以上改进方法，本文针对RRT 算法随机采样存在的大量无效采样以及路径不最优等问题进行改进，以二维环境中的移动机器人为载体进行算法验证。通过引入偏向目标的随机点采样方式改进算法采样的无目标性，使算法能够加速收敛。采用剪枝操作和多项式插值的方法对路径进行优化处理，使路径平滑，更利于机器人执行。

2 基本算法描述

快速随机扩展树法是一种基于采样的全局路径规划算法，其节点扩展示意图如图1（a）所示。首先初始化随机树，将起始点和目标点插入运动空间中，把起始点xinit作为随机树的根节点，然后在运动空间中随机选择一个点xrand，再在随机树中搜索出距离xrand最近的节点xnear，将两点连接起来，如果两者间的距离小于或等于设定的步长则将xrand直接设为新节点xnew，否则在连线上取距离点xnear为步长的点作为xnew。之后再判断新节点以及连线是否与障碍物发生碰撞，若碰撞则删去该新节点再重新选择随机点继续如上步骤，若没有发生碰撞则将xnew节点和边Ej插入随机树T 中。如此不断扩展随机树，直至节点包含目标节点或进入目标区域。最后反向追溯到根节点便可以在随机树中找到一条由从初始点到目标点的路径。

从图1（b）可以看出，RRT 算法规划的路径存在较多折角，并不能保证机器人的速度连续性，不利于机器人执行，而且此路径也不是到达目标点的最近路径。其原因在于，RRT算法是在地图范围内随机撒点，然后将无碰撞的一系列点连接起来构成路径的。其过大的随机性不仅造成路径不最优，而且因为探索了大量无效的采样点而导致其规划效率降低。

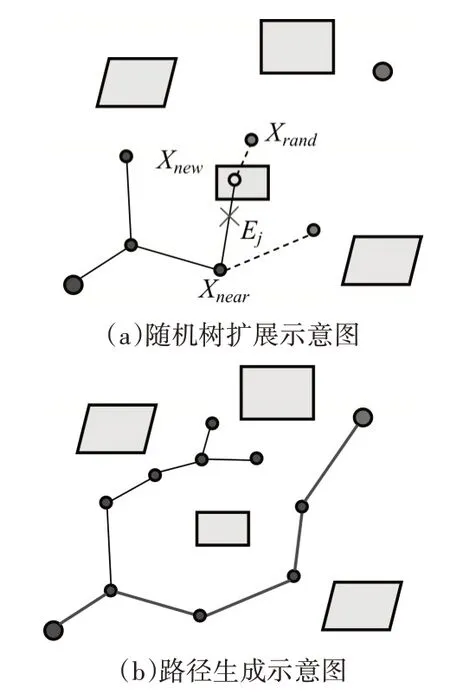
图1 RRT算法示意图

3 改进的RRT算法

基本的RRT 算法随机性过大，在复杂的环境下其收敛速度显著下降，且规划的路径大多蜿蜒曲折，并不是一条最优路径。因此，本文首先对其采样方式进行改进，并对其规划的路径进行剪枝处理以及多项式曲率拟合处理。

3.1 偏向目标的采样

相对于RRT 算法的均匀随机采样，本文引入了一种偏向目标的采样方法，具体如图2 所示：首先继承了RRT 算法的采样方式，在地图中随机获得一个采样点xtrand，然后将此随机点与目标点连接起来，再在两者之间的连线上随机采样一个点作为最终的随机点xrand。在完成随机点采样后，本文算法的碰撞检测策略，随机树扩展方式以及路径的回溯创建均采用与RRT 算法相同的方法。本文改进的采样方式不仅能够保证一定的随机性还能使随机树向着目标点扩展，减少大量无效的采样，加快算法的收敛速度。

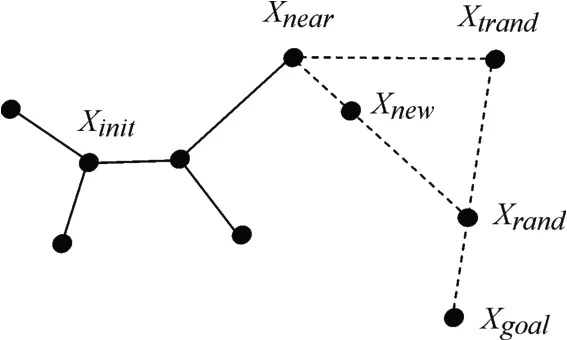
图2 偏向目标采样示意图

3.2 路径剪枝处理

由RRT 算法规划出的路径存在许多角度突然变化的折线，有些节点之间并不存在障碍物，而轨迹也呈弯折状，如图3 所示，其导致中间存在许多没有必要的节点，如图中node1和node2。可以将其间冗余的中间节点从路径中剔除以缩短路径的长度，同时也可以在一定程度上平滑路径。

综上所述，本文基于多元交通方式运用改进的两步移动搜索法相比于邻近距离法对养老服务设施可达性进行了修正研究，同时对老年人选择不同出行方式进行对比分析，并从公平性视角对武汉市养老服务设施布局进行评价.主要研究以下问题：1) 采用两步移动搜索法与最小邻近距离法测度可达性的相关程度如何.2) 受不同交通方式的影响，公共服务设施可达性有何差别.3) 武汉市养老服务设施可达性空间格局是怎样的，哪些公平性较差区域需要合理布局养老服务设施资源.

图3 剪枝处理示意图

路径的起始点和目标点附近都可能存在冗余节点，因此本文的剪枝处理从路径的第二个节点开始。首先以路径的起始点为根节点，从第二个节点开始依次连接起始点并检测其连线是否与障碍物发生碰撞。若没有碰撞则一直检测后续节点，直至检测到某个节点与起始节点的连线与障碍物发生碰撞。此时将上一个节点xpre与当前节点xcur依次插入一个新的路径储存变量path2，然后将起始点与节点xpre的连线作为新路径。同时把当前节点置为新的根节点，再继续对剩余节点做碰撞检测，以此循环，直到目标节点加入检测后跳出循环。此时path2中储存的即是剪枝处理后的新路径节点。

3.3 多项式路径平滑

对于RRT 算法规划的路径，其存在不光滑的转角，由于动力学约束，机器人跟随此路径走到转角处必须先停下来，再一次性转至对应角度才能继续行走。然而这并不是想要的结果，因此本文针对这一问题，在3.2 小节剪枝处理的基础上采用多项式对路径的转角处进行平滑处理。本文采用五次多项式进行路径平滑处理，具体如下：

1）五次多项式插值：

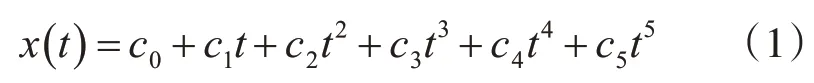
2）将上式分别求一阶，二阶导得

3）边界条件：

多项式边界条件如表1所示。

表1 多项式边界条件

代入边界条件并写成矩阵形式得：

此步基于剪枝处理得到的路径进行处理，首先遍历路径中的所有节点与边，找到包含转角处的节点以及紧邻此节点的两节点作为五次多项式的边界条件。然后对此转角进行曲率插值拟合，从而得到一条光滑的曲线用以代替转角。

3.4 算法总体实现

基于上述改进，本文算法的整体实现如下表伪代码所示，主要包括初始化随机树，在无碰撞的空间中扩展随机树，反向搜索随机树，找到一条路径，然后再对路径进行剪枝处理以及多项式平滑处理。

4 实验与分析

为了验证算法有效性，本文将以上三种改进措施依次在Matlab平台上实现，并将实验结果与未改进前的算法进行对比，从而分析改进的效果。此外还将改进的整体算法与RRT、RRT*、informed RRT*算法进行对比分析。本实验运行环境：64bit Windows10 操作系统；Matlab 2016a；处理器AMD RYZEN5 2500U；主频2.0GHz；内存8GB。

4.1 改进采样方式的实验

此部分验证改进采样方式的效果并与RRT 算法作对比，本实验中算法的迭代次数均设为3000，随机树的扩展步长设置为0.35，终止的条件为找到目标节点或达到最大迭代次数。实验结果如图4所示：其中深色和浅色的点分别表示起始点和目标点，细实线表示随机树，粗实线表示规划的路径。

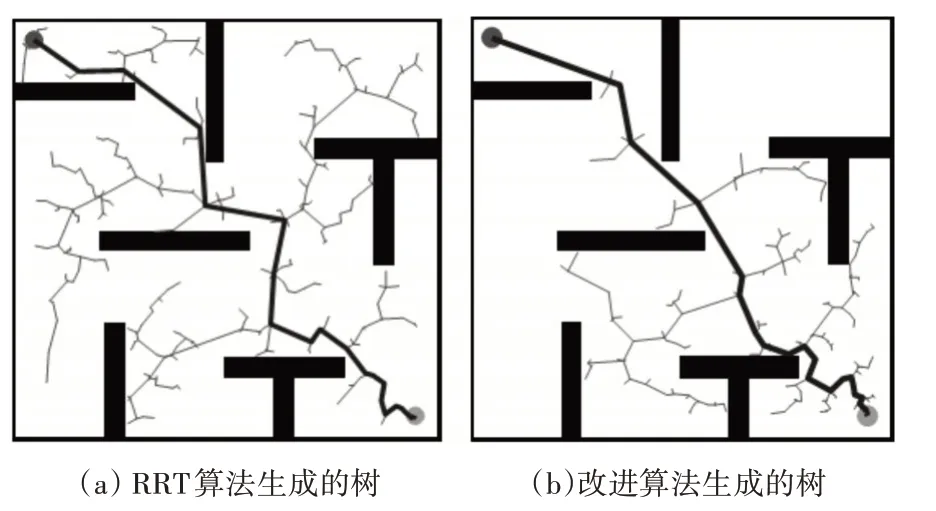
图4 改进采样方式的算法

表2 改进算法伪代码

从图中可以看出，未改进的算法生成的随机树均匀的遍布整个地图，而改进算法的随机树朝着目标点生长，在目标点区域附近其密度明显高于地图上其他区域。对两种算法花费的时间以及规划的路径长度进行了统计。由于快速随机扩展树算法的随机性，每次规划的路径和所花时间基本都不同。因此，实验中两个算法都运行了五次然后取平均值，其结果如表3所示。

表3 改进的RRT算法与未改进的算法对比

由以上图表可以看出，改进后的算法在搜索路径时具有目标偏向性，避免了大量无效的采样，因此其规划效率显著提高。对于所规划路径的长度，改进算法也缩短了不少。在平滑度优化方面两者差异并不大但也有所优化。

4.2 路径剪枝处理实验

此部分实验单独考察路径剪枝处理给算法带来的变化。环境地图采用与上小节相同的地图，大小为800*800，最大迭代次数、扩展步长、算法终止条件均与4.1小节相同。其实验结果如图5所示。

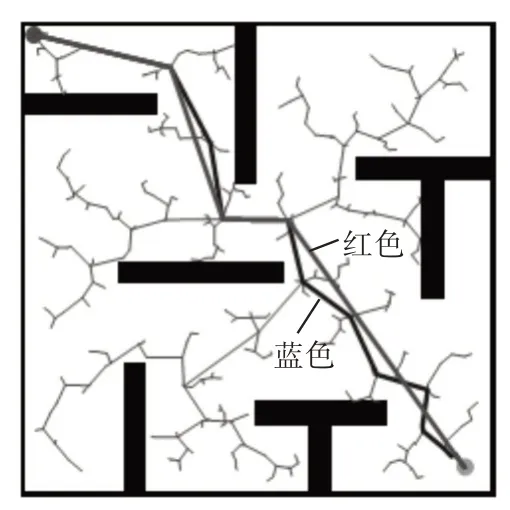
图5 剪枝处理实验图

实验中将改进前后的路径画在同一张图里进行比较，其中蓝色粗实线是未优化的路径，红色粗实线是经过剪枝处理后的路径。从图中可以明显看出，蓝色的路径存在较多弯折的冗余线段，改进后的算法将不必要的弯折部分滤掉而直接用直线连接起来，如此可以有效的缩短路径的长度，并且使路径的平滑度得到一定的优化。

4.3 多项式路径平滑实验

本节实验参数与4.1 和4.2 小节的实验设定相同，地图与前两节保持一致。多项式插值是在经过剪枝处理后的路径上进行的，此处保留未优化与部分优化的路径，将三条路径进行对比。障碍物假设已经做过膨化处理，而机器人视为一个质点。实验结果如图6所示。

图6 多项式路径平滑实验图

图中绿色粗实线即为经过多项式平滑处理后的路径，红色是经过4.2小节剪枝处理后的路径，蓝色为未改进算法的路径。从图中可以看出，改进后的算法在存在折角的路径处进行了曲率拟合，与原算法的路径相比，本文改进算法对路径进行了有效的光滑，路径长度也同时得到优化。

4.4 总体改进算法的实验分析

以上三小节采用控制变量的方法分别验证了三个改进措施的效果，本节将三种措施综合起来，验证改进算法的整体效果。首先依旧采用800*800 的地图，运行结果如图7 所示。其中绿色粗实线为优化后的路径。从图中可以看出该路径虽不是最短路径，但其比较光滑。此外随机树朝着目标生长，非目标区域的无效采样树非常稀疏，搜索效率明显提高。

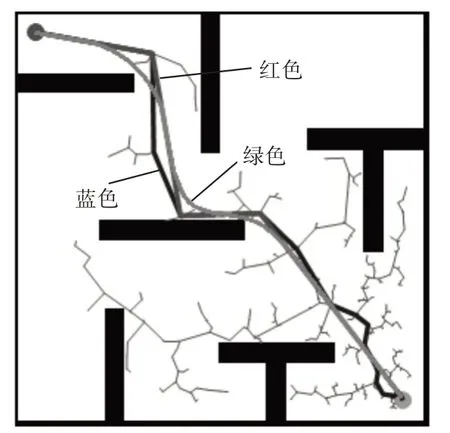
图7 改进算法整体效果图

其次，本文将RRT 算法、RRT Connect 算法、RRT*算法与改进算法进行对比。实验中采用了一张100*100 的地图，地图在目标周围设计了一处方形障碍物模拟凹形通道。迭代次数与步长等参数四种算法均保持一致，结果如图8所示。

图8 四种算法对比图

从图8 和表4 可以看出，路径光滑度本文改进算法最好，RRT*算法也不错。从平均路径长度来看，本文改进算法最短但与RRT*算法相差不大，且都不是最短路径。RRT Connect 算法和RRT 算法由于都是随机性的，所以两者路径长度也相差不大。对于规划效率来讲，由于RRT Connect 算法是从起点和目标点同时搜索的，所以其耗时远远低于其他算法。综上，本文改进的算法不但优化了路径而且还在一定程度上提高了算法的规划效率。

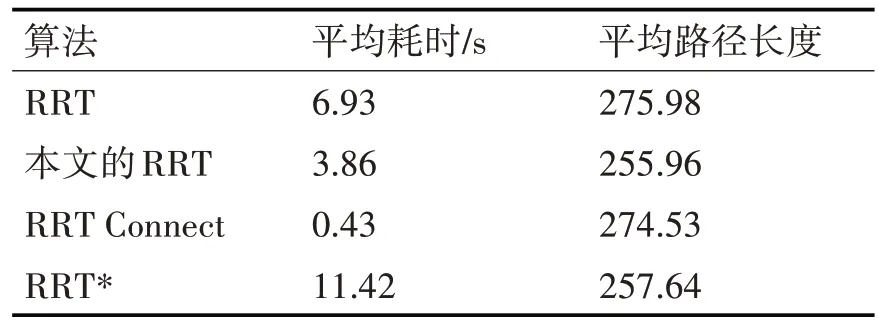
表4 四种算法对比表

4.5 ROS平台仿真实验

本节将改进的算法在ROS上实现，为移植到真实机器人上做准备。导航的整体框架采用ROS 中的navigation stack，将其中的gloable_planner替换成本文的改进算法。此处采用stage 仿真工具搭建仿真环境，并且将RRT 算法和本文算法进行对比，具体效果如图9 所示，从图中可以看出本文算法明显优于RRT算法。

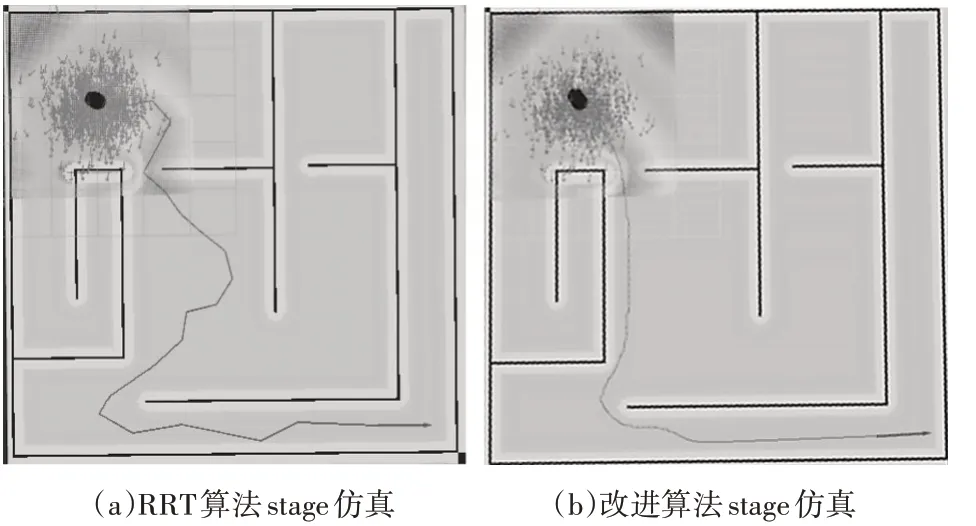
图9 ROS仿真效果图

5 结语

路径规划问题是移动机器人研究的关键问题，本文提出一种改进的RRT 算法，引入偏向目标的采样策略，既保证采样点的随机性又提升其目标偏向性；对冗余路径节点进行剪枝处理，滤除无效的弯折路径；采用多项式插值的方法，对路径进行曲率平滑处理。最后通过仿真实验验证了本文改进算法的效率不仅显著提高，而且所得路径的光滑度也大大提升。

本文研究主要针对于优化RRT 算法规划的路径以及提高算法的规划效率，实际机器人中有很多需要考虑的问题，后续研究可以扩展到动态环境下的路径规划，将更多约束考虑在内，以提升机器人在更复杂的环境下的路径规划能力。