120 GHz 超宽带毫米级高精度雷达液位算法

李国栋 王雪楠 仝盼盼 毕 欣

（1.中国昆仑工程有限公司大连分公司；2.大连东软信息学院健康医疗科技学院；3.同济大学汽车学院）

近年来，石油化工行业不断发展，石油化工产品的生产和存储环境逐渐复杂，油品具有易燃易爆的特点，油品存储罐容量较大，一般在千吨级甚至万吨级。 在油品生产过程中，需要时刻准确掌握油品储罐的状态，若误差较大会给企业带来较大的经济损失，同时也容易造成事故安全隐患。 因此，罐内液位高度的测量精度不但直接影响企业的经济效益，而且直接影响企业的生产安全。

石油化工行业一直以来都是采用液位开关来进行油品储罐的液位报警，其缺点是在运行过程中开关状态难以有效监测， 平时难以维护，而能够连续不间断地对液位进行测量的自动化仪表则可以对相关油品储罐内的液位变化情况进行实时动态监测并能够对仪表自身的工作状态进行实时监测报警，因此可靠性更高。 但是现有的液位连续测量仪表存在一些问题。 例如，静压液位计精度较差，主要是由于受测量介质密度和温度的影响较大；磁致伸缩液位计一直以来在市场上普及不广，主要是该液位计采用与测量介质接触的测量方式，安装和维护要求较高，而且主要适用于非腐蚀性介质测量，不适用于粘稠性介质； 伺服液位计同样有接触式液位计的各种弊端，也不适用于腐蚀性和粘稠性介质。

雷达液位计因采用非接触式测量且不需要传输媒介， 故能够应用于易挥发介质的液位测量，不受罐内介质挥发性气体的影响，并且不受罐内液体介质的浓度、密度等相关物理特性的影响。 随着技术和工艺的进步，其价格逐步降低，应用范围越来越广。 雷达液位计能适应恶劣的应用环境，不但抗干扰能力强，而且测量精度较高，所以在石油化工行业得到了广泛应用［1，2］。

近年来，石油化工行业对雷达液位计测量精度的要求越来越高， 而目前主流的26、80 GHz雷达液位计存在一些测量精度问题。 为此，笔者基于一种新的120 GHz超宽带雷达液位计， 并结合高精度Chirp-Z变换算法，从而达到提高雷达液位计在油品储罐中液位测距精度的目的。

1 雷达液位计工作原理

雷达液位计的天线定向发射电磁波，这些电磁波经过被测液体介质表面反射后，被雷达天线接收。 雷达所测距离R的计算式如下：

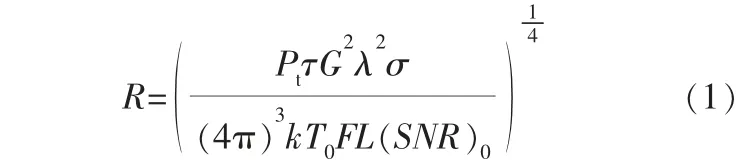
式中 F——噪声系数；

G——天线增益；

k——玻尔兹曼常数，k=1.38×10-23J/K；

L——系统损耗；

Pt——发射功率；（SNR）0——信噪比；

T0——标准温度；

λ——波长；

τ——传输的脉冲宽度；

σ——雷达散射截面。

罐体内介质、 介电常数和温度都会对探测精度产生影响， 需要综合考虑。 文中只考虑常温状态，而实际工况中，除了考虑这些影响外，还需要考虑实际环境和测量介质。 不同介质［3］环境下，雷达信噪比随雷达探测距离的变化关系如图1所示。

图1 不同介质环境下信噪比随雷达探测距离的变化关系

由图1可知，在不同的介质环境下，随着探测距离的增加， 雷达探测信号的信噪比随之降低，表现为探测精度的降低。

线性调频连续波雷达［4，5］的发射频率带宽为4 GHz，距离分辨率3.75 cm，最高发射功率10 dBm，探测距离最高达100 m。 发射波形方程如下：

式中 A0——幅值；

f0——雷达载频；

k0——调频斜率；

T——周期；

φ0——初相位。

雷达信号在经过距离为R的传播后， 与回波信号之间会产生时延td，则有：

回波信号经过混频、 中频基带信号经过FFT后，得到如图2所示的信号频域图。

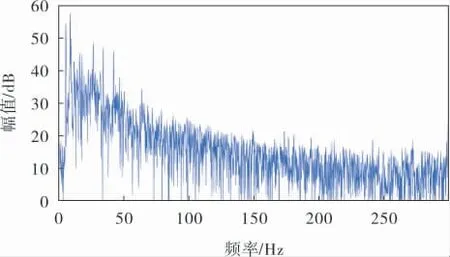
图2 信号频域图

由于雷达测距的精度主要依赖于对雷达收发信号混频后所得的差拍信号（频率与目标距离线性相关的信号）， 因此可以利用差拍信号的频率对目标进行测距，从而把对测距的精度转换为对差拍信号进行数字信号处理的问题［6］。 传统的液位计测量都是利用FFT处理实现的， 造成频谱处理的精度受到栅栏效应、泄漏效应、混叠效应及量化结果误差等因素的影响，导致对频谱的分析精度不高，并且测距精度很难提高。 量化误差和混叠效应是在进行AD转换过程中引起的，而泄漏效应与栅栏效应是FFT算法进行数字信号处理时不可避免的问题，导致频谱的实际曲线与理想曲线之间具有偏差。 如图3所示， 红色点是进行FFT处理后得到的信号强度点， 绿色点是因为栏栅效应而丢失的点，在进行FFT处理后不可见，从而产生ΔR/2的测距误差，因此雷达液位计无法满足高精度测量场合的要求。

图3 实际频谱点与理论频谱点示意图

2 Chirp-Z变换信号处理算法

石化行业中存储罐体对雷达液位计的测距精度要求很高，需要控制在1 mm以内。为此，笔者提出一种面向120 GHz超宽带毫米波液位雷达的高精度Chirp-Z变换算法，通过细化主频频率区域的频谱以减小FFT算法的误差影响。

2.1 Chirp-Z变换算法原理

Chirp-Z变换采用的是螺旋线式采样方式，可与FFT算法结合从而对雷达差频信号进行快速计算。 Chirp-Z变换的算法原理如下。

已知序列x（n），0≤n≤N-1，利用Chirp-Z变换之后可得：

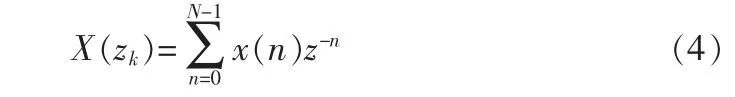
采样点zk为：

式中 A、W——任意复数；

M——主频局部相应的频谱点数。

A和W分别表示为：

将式（6）代入式（5）得：

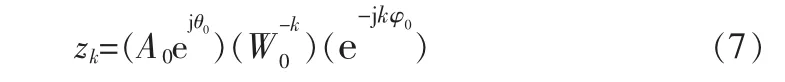
将序列zk分解后，得到如下各项：

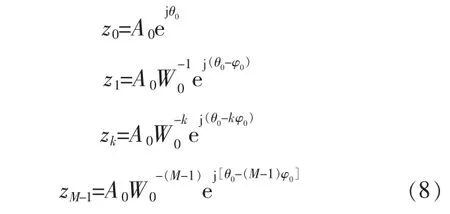
其中，z0为采样的起始点；A0为z0矢量半径的模值，且A0≤1；φ0为相邻两采样点的角频率差，当φ0为正值时，则表示变换的螺旋线向外旋转，否则表示螺旋线向内旋转；θ0为z0的相角；W0为变换螺旋线向外弯曲或者向内弯曲的伸展率。 若W0＜1，则螺旋线向外弯曲；若W0＞1，则螺旋线向内弯曲；若W0=1， 则表示变换螺旋线正好是一段圆弧，且其半径为A0。

综上分析可知，通过增加FFT的点数，可以提高系统的距离测量精度， 计算总量公式为MNlog2MN。 若对M点进行傅里叶变换，需要完成MN次复数乘法与M（N-1）次复数加法，且系统的计算量要随M和N的增加呈指数级增长。 Chirp-Z变换的计算总量公式为Nlog2N+2（M+N）+（N+M）·log2（N+M），据此可将Chirp-Z变换进行相应的处理，推导为求卷积形式的FFT变换，从而减少系统相应的计算量，并提高系统的测量精度。

2.2 算法流程

首先通过脉冲压缩、加窗处理及质心聚类等方法，确定罐体和测量环境中的干扰及真实液位FFT峰值位置［7］，之后在选定的峰值位置处进行CZT变换，进行频率细化以实现高精度测量［8］。

算法的基本原理和步骤如下：

a. 预处理。 为抑制回波信号的旁瓣，采用特定窗函数对罐体内液位回波的时域信号进行数据处理，并对经过旁瓣抑制的信号进行频域变换A（m）=FFT［x（n）·w（n）］，由此可得到复数频谱值，由于对信号进行搜索时只对频谱的幅值进行检测，因此，对信号取其幅度值｜A（m）｜。

b. 针对不同环境下系统线性调频信号线性度漂移的问题，利用算法构建频率校准和补偿曲线，并利用曲线C（m）对预处理频谱｜A（m）｜进行校正和补偿处理P（m）=｜A（m）｜·C（m）。 在相同罐体环境内，由于不同高度的液面回波信号存在不同程度的衰减，因此，为提高系统的测量精度，使得线性调频信号具有稳定的线性调频斜率，需要对频谱进行校准和补偿处理。

c. 为提高测量精度，将不同高度的液位频谱划分为若干子频率集合［fi，fi+1］，其中［f0，f1］∪［f1，f2］∪…∪［fN-1，fN-2］构成了整个罐体测量高度内液位回波信号频率的集合。 考虑到部分工业罐体内还存在搅拌、泡沫等干扰工况，因此针对不同高度的频域频谱集合，采用不同的回波峰值搜索方法。

d. 对经过恒虚警率 （Constant False-Alarm Rate，CFAR） 近区超过检测阈值的频谱进行预处理，逐步延伸到最大测量距离。 针对不同高度的频率子集可采用差异化规则， 并针对近区过CFAR阈值频率集上的频谱， 进行频率相关的预处理，计算式如下：

式中 fi——近区回波超过CFAR阈值的频谱分量；

fref——相关参考频率；

fT——CFAR门限；

S——不同探测距离回波峰值的频谱集合。

对搜索到的过门限的频谱分量， 求频谱质心：

从近区第1个频谱峰值开始， 建立质心凝聚的中心点，并记录质心中心的数量，通过配置质心中心的宽度阈值，可以抑制噪声信号局部极值的干扰。如果相邻质心｜Qi-Qpeak｜＜Th（其中Qi为质心频谱值，Qpeak为频谱峰值，Th为宽度阈值），则对质心对应的频谱值进行合并，并取最大值对应的频谱；反之，如果质心频谱值与质心距离大于宽度阈值，则建立新的质心频谱。 最后确定罐体内质心中心的数量以及对应的频谱值。

e. 经过质心凝聚算法后，确定对应的频谱峰值点，结合罐体测量高度和安装干扰位置，利用每个质心对应的频谱位置，估计罐体内液位高度的主频和干扰频率，在主频频率点附近设定所需频率范围Qi-peak∈［f1，f2］，利用Bluestein等式对选定范围内的频谱进行Chirp-Z变换，对选定质心指定范围的频率进行频谱信号的细化，提取相应质心的前M点，并乘以，计算得到M个点对应的频谱。 利用变换后的频谱，可进一步精确确定主频频率：

综上所述，利用本节提出的算法，可得到直接利用FFT变换后的频谱、利用CZT变换细化后采样点的频谱及利用CZT变换后的细化频谱，如图4所示。

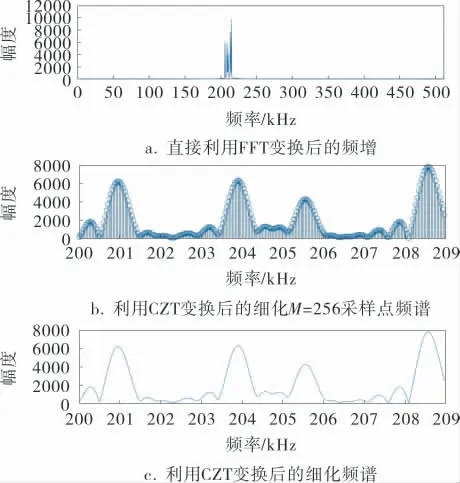
图4 FFT变换频谱和CZT变换后的细化频谱对比

由图4可知，采用CZT变换后的细化频谱相较于直接利用FFT算法所得到的频谱， 可以更精确地确定主频频率，从而实现目标的高精度测距。

3 算法验证

考虑到实际雷达液位计的可探测距离在100 m以内， 而罐体中的液面平稳且罐体长度一般为15～30 m， 故采用120 GHz两线制调频连续波雷达，雷达与被测物呈垂直角度。 雷达的基本参数为：调频带宽4 GHz，调频周期25 ms，采样点数4 096点。 目标参数见表1。

表1 目标参数

测量结果和误差见表2。

表2 测量结果和误差

分析表2可得，随着目标物距离的增加，采用CZT变换算法对目标物的距离进行测量相较于直接采用FFT算法可以获得更高的测距精度， 且测距精度在0.5 mm以内， 测量的相对误差不超过2%。 而在雷达液位计的实际运行过程中，由于罐体内环境是多样性的，因此，要根据罐体中的环境对雷达液位计的参数进行具体设定和调整，从而使液位计的工作达到最优效果。

测试结果表明，在同等条件下，采用CZT算法的测距精度较FFT算法的测距精度高14倍。 笔者提出的基于120 GHz超宽带毫米波液位雷达的高精度Chirp-Z变换算法可以在综合考虑工业现场多工况的干扰以及介质的介电常数的情况下，利用脉冲压缩、加窗、质心聚类及波形跟踪等多步骤信号处理进行融合， 从而使液位计在保证高精度测试需求的同时， 能够提高系统的实时性和鲁棒性。

4 结束语

面向石油化工以及电力系统超宽带高精度液位测量领域， 基于120 GHz超宽带毫米波液位雷达，旨在解决化工油品储罐中液位的高精度计量问题。 笔者提出了一种将CZT与超宽带雷达特性结合的方法， 可实现0.5 mm以内的测量精度，并在现场实际应用中取得了稳定的效果。 CZT算法具有分辨率高、计算灵活性好及计算速度快等优势，因此在频谱计算、窄带分析、频率探测及信号识别等领域将具有广阔的应用前景。