渐变式椭球体区间预测控制
邓锴彧 万 鑫 罗雄麟
(中国石油大学(北京)信息科学与工程学院)
模型预测控 制 (Model Predictive Control,MPC)是20世纪80年代初发展起来的一类新型计算机控制算法[1,2],该算法直接在工业过程控制实际应用,并在与工业应用的紧密结合中不断完善和成熟。 模型预测控制算法由于采用了多步预测、滚动优化及反馈校正等控制策略,因此具有控制效果好、鲁棒性强和对模型精确性要求不高的优点,这些优点决定了该方法能够有效地应用于复杂工业过程的控制,并且已在石油、化工、冶金及机械等过程控制系统中成功应用[3~5]。
实际工业控制应用中,MPC对被控变量(CV)的控制方式主要有设定值控制和区间控制[6,7]两种。 设定值控制能够将被控变量严格控制在理想的目标值, 适用于具有严格控制指标的被控变量,但对于被控变量的严格控制又使得设定值控制具有自由度低和鲁棒性差的缺点,在工业过程遇到扰动的情况下,控制性能会大打折扣,被控变量剧烈振荡,影响产品性能与质量[8~10]。 在一些工业领域,被控变量在一个特定范围内波动对控制过程的影响几乎相同,对于此类被控变量,无需将其控制到一个严格的设定值,而是将其控制在一个范围内即可,即区间控制[11]。 区间控制框架下的系统性能指标与设定值型控制指标不同[12,13],控制策略也不同。 当被控变量到达设定区间内时,控制器不再产生控制作用;当被控变量在设定区间外时,控制器产生强控制作用,使被控变量快速回到设定区间。 用区间控制代替设定值控制会使系统的鲁棒性和自由度大幅提高。
近些年来, 为了更好地满足工业控制要求,区间控制算法已成为控制理论的热门研究课题,并且在实际应用中也取得了巨大发展。 文献[12]研究了闭环系统的稳定性。 文献[14,15]采用多层结构设计具有区间控制特点的区间控制策略,该策略中上层的优化器可以计算最优工作点,而MPC控制器可以在约束条件下将系统的状态驱动至该点处。 文献[16]设计了一种具有区间跟踪特性的区间控制策略,使用距离范数来确保递归的可行性和局部最优性,并通过仿真实验验证了该策略的性能。 文献[17]设计了一种基于软约束的区间控制算法,降低了违反区间控制目标的频率,并提高了闭环系统的稳定性。 文献[18]基于被控变量进入目标区间后还有额外的自由度,根据这种自由度设计优化策略,来提高区间控制系统的经济效益。 文献[19]提出一种软约束处理方法改善控制品质,实现了区间控制。 文献[20]提出一种稳定的区间MPC控制器,该方法的代价函数中包括输入输出的稳态经济目标。 文献[21]提出一种基于梯形区间软约束的多目标预测控制算法, 该算法将设定值控制和区间控制相结合,设置梯形区间,并建立两个目标函数,有效减小了瞬时偏差的波动幅度,缩短了达到目标值的时间。
但是对于被控变量从初始状态到目标区间这一动态响应过程,现有文献大多只是让被控变量满足过程约束,这就可能导致被控变量在到达目标区间前产生很大的超调量。 使系统在不产生超调量的前提下快速进入目标区间成为亟待解决的问题。 为了解决这个问题,进一步提高多输入多输出系统的整体性能,同时兼顾系统的稳定性与快速性,笔者提出基于渐变式椭球体区间约束的预测控制算法。
1 问题的提出
现有的区间预测控制算法的研究更多关注目标区间形状的设计,或对预测时域进行分割产生不同的控制策略。 对于多变量系统,也有学者通过改变每个控制变量的权重来达到对不同变量的不同控制效果;也有将设定值控制与区间控制结合,不同的输出变量采用不同的控制策略来达到控制效果; 亦有将控制过程分为两个阶段,从初始工作点到目标区间这一阶段注重响应的快速性,当被控变量进入目标区间后考虑系统的经济效益等。 这些区间控制策略本质上都是在被控变量超出目标区间时用强控制作用使被控变量快速返回目标区间。 而控制器对于被控变量从初始工作点到目标区间的状态迁移过程只是让其遵守相应的全局约束。 这样的控制策略无法解决系统控制效果快速性与稳定性之间的矛盾。 被控变量快速进入目标区间可能导致系统超调,而期望系统平滑进入目标区间又导致响应时间变长。
两种区间控制策略对应的不同闭环轨迹如图1所示。 策略Ⅰ采用预测时域P较小的区间模型预测控制器, 输出变量y能够快速进入区间控制目标Ysp。 同时,较小的预测时域P使得输出变量y具有一定惯性,导致其突破了Ysp的边界,直到t1时刻系统才达到稳定。 策略Ⅱ采用了较大的预测时域P,可认为闭环系统处于过阻尼状态,此时能够避免超调现象, 但会使系统达到稳定的时间变长,即t2>t1。

图1 区间模型预测控制闭环轨迹
为了能够改善上述问题,使得系统对于输出变量控制效果在保证安全的前提下响应兼具快速性与稳定性,笔者设计了一种具有渐变椭球体约束的模型预测控制策略,本课题所设计的模型预测控制策略使得系统的开环预测轨迹在进入设定区间之前不再仅遵从系统的全局约束,而是使其处于性能可设计的渐变式椭球体区间序列约束内部,用以避免产生超调并提升系统的响应速度,缩短响应时长。 在该策略下系统的闭环轨迹如图2所示。

图2 渐变式椭球体区间模型预测控制闭环轨迹
图2所示的闭环轨迹存在一组由椭球体序列构成的约束通道,使得被控变量沿着预设通道从初始状态到达目标区间,并且能够快速进入目标区间,同时不会产生超调。
这样做的意义在于确定了能够使系统达到稳态的预测时域P的合适范围后, 保证系统控制效果稳定的前提下对于提高系统响应速度不用再调整预测时域P, 而是通过改变椭球体序列中约束椭球体个数N来使得系统响应速度得到提升,并且相应地减少超调量,使得系统输出变量平滑地进入目标区间。
渐变式椭球体区间模型预测控制算法的各部分功能框图如图3所示。 图3中性能可调的协调器用以在线产生k时刻渐变式椭球体开环轨迹约束集Y(yc,),该渐变式约束集能够保证系统的开环预测轨迹处于性能可设计的约束区间内部, 用以避免产生超调并提升系统的响应速度。

图3 基于渐变式椭球体约束的区间模型预测控制功能框图
针对椭球体控制目标给出如下定义:

其中,Y⊂Rn表示控制目标区间;y⊂Rn表示最优稳态点;yc⊂Rn表示系统任意工作点。
定义3 给定椭球体控制目标Ysp, 若存在控制器u(k)=G(x(k))使得闭环系统x(k+1)=Ax(k)+Bu(k),y(k)=Cx(k)满足:对于∀γ>0,∃T0>0使得∀t≥T0,均有dist(Y,y)≤γ成立,则认为,椭球体目标控制系统是稳定的。
2 椭球体区间目标的构造与坐标变换
常用的区间控制目标是盒子型目标,盒子型目标区间边界不光滑且存在断点,而且由于顶点的存在,无法在渐进稳定的平衡点处构建较大的吸引域,而且这些断点造成区间控制目标无法用解析函数的形式表示,所以只能通过比较与判断相结合的方式进行位置的确定以及空间中的距离的求解,即都需要将当前状态变量在空间中的位置与目标区间边界的距离逐一比较,才能进一步计算当前状态与区间控制目标之间的距离。 对于被控变量是否进入目标区间也需要进行判别,这就大幅增加了计算难度。
替换后的椭球体控制目标是具有光滑的表面并能用一个光滑的函数表示的凸集区间,在求取空间中的状态变量与椭球体区间控制目标的距离时,能够直接采用解析的方法获得。 因此,笔者所提算法采用椭球体型目标区间。
2.1 椭球体目标区间构造
由于生产工艺条件或过程硬件物理性能具有极限承受力而产生的约束称为过程约束,这种过程约束一般表现为盒子型。 过程约束Ψ的表达式为:

其中,yi表示状态向量y的第i个分量,、分别表示第i个分量的最小值 与最大值,I[i,n]为整数集合。
现以控制系统的初始工作点yinit与最优稳态点ysp为中心构建椭球体形式的区间, 如图4所示。

图4 椭球体区间构造示意图
其中,rsp、rinit分别表示以最优稳态点和初始工作点为中心的椭球体区间的半径。
令所构造椭球体区间半轴长度与过程约束边长满足如下关系:

2.2 椭球体区间坐标变换
根据定义,以最优稳态点ysp为球心构造的目标椭球体区间为基准进行坐标变换,其解析形式表达式为:

其中,Λsp表示输出偏差加权阵,正定阵。
根据矩阵的基本性质,椭球体目标区间标准形式为:

其中,I表示单位矩阵。 令y′sp=Λspysp,y′=Λspy,则其表达式进一步可以写为:

坐标变换后以y′c为球心,r′c为半径的闭合球体表示为:

式(7)可以视作一个球体,那么Y(y′sp,I)与B(y′sp,r′sp)均表示目标球体区间。
过程约束与初始椭球体区间,做同等坐标变换后变为一个正方体型的过程约束和一个球体初始区间,其表达式分别为:
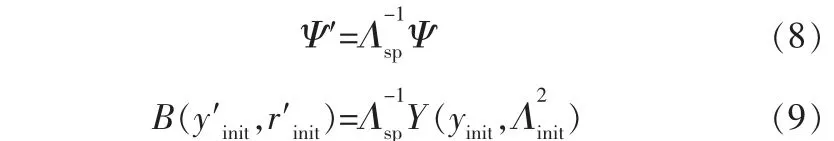
区间控制下系统状态处于目标区间之外时会以距离度量函数为性能指标,该指标表示系统当前状态与区间控制目标之间的距离。

由式(10)可以看出,当y′c在目标球体区间内部时dist(B(y′sp,r′sp),y′c)恒为零,y′c在目标球体区间外部时dist(B(y′sp,r′sp),y′c)表示y′c到目标球体区间B(y′sp,r′sp)边界的最短距离。
则对应优化问题的性能指标函数为:

其中,ΔU为控制变量增量,Δu(k+j|k)表示未来j时刻的控制作用的增量。
2.3 渐变约束序列在线生成

3 渐变式球体区间预测算法的实现
3.1 渐变式球体区间优化问题的描述
y^′P(k+i|k)(i=1,…,P)表示以k时刻为基准未来i个时刻的开环预测输出。系统在k时刻的P个开环预测输出(k+i|k)(i=1,…,P)使它们受到第k+1~k+P这P个球体的约束。当时刻变为k+1时,系统从k+1时刻开始未来i个时刻的开环预测输出y′P((k+1)+i|k)(i=1,…,P)使它们受到第(k+1)+1~(k+1)+P这P个球体的约束。把这种渐变式球体区间约束策略记作φ′(B(y′c,R′c),(k+i|k))。
这种约束策略与系统当前时刻k、 系统的预测时域长P和球体约束个数N相关, 当k+P<N时,系统在k时刻的P个开环预测输出均未到达目标球体区间, 所以球体区间约束序列仍要向前滚动。 φ′(B(y′c,R′c),(k+i|k))表示如下:

当k+P≥N时,系统第N-k+1时刻的开环预测输出会进入目标区间, 使其受到第N个球体区间的约束, 令N-k+1时刻之后的开环预测状态也受到第N个球体区间的约束, 此时实际上系统输出已经到达符合要求的目标区间,则φ′(B(y′c,r′c),(k+i|k))可表示为:


根据以上分析, 系统预测时域P一般取动态响应时长的1/4,P确定后影响该算法对系统控制效果的因素为球体序列中球体个数N。当N发生改变时,笔者提出的算法对系统的控制效果将会改变。 系统开环预测输出值受球体区间约束序列的滚动次数为N次。可以预见的是,随着N的增大,球体区间约束的滚动次数会增加,系统的响应轨迹会越来越平滑,能够完全在球体约束序列形成的通道中进入目标区间,相应地系统响应时间会变长。如果N过小,被控变量响应过程中在某些时刻会超出预测通道产生振荡。
本研究的优化问题表示为:
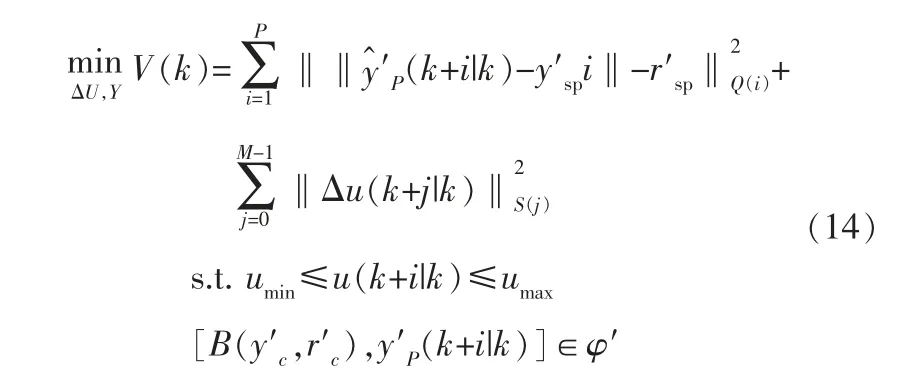
优化目标函数包括两部分:状态变量到目标区间的距离度量函数与控制增量的变量。 约束条件中,[B(y′c,r′c),y′P(k+i|k)]∈φ′是本算法中开环预测状态应该满足的约束条件,由于此条件满足过程约束:

所以满足此条件的开环预测状态必然满足过程约束。 不同情况下的球体区间约束序列为:

表现形式如式(12)、(13)。
3.2 区间预测控制优化性能指标求解
由于本算法对应优化问题并非标准形式,所以需转化为标准形式后进行求解。
假设预测控制采用如下线性时不变离散状态空间模型:

2.2节中分析了对控制系统整体做坐标变换不会影响系统的控制效果,对系统模型整体左乘并做与渐变式椭球体区间同等的坐标变换得到新的模型:

则系统状态的预测表示成矩阵形式为:

此时系统输出的预测表示为:

即:



未来M个控制增量的动态矩阵Γ为:


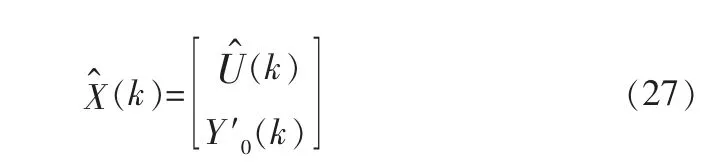
性能指标函数可以写为:


const为常数部分, 对优化问题不构成影响,可以忽略,所以新的性能指标函数为:
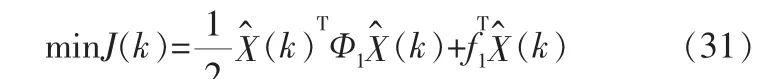
本算法预测控制中输入约束条件为:

记:


输入约束条件转化为:

k时刻对应的开环预测输出应该满足的条件描述如下。
假设约束球体个数足够多,即N取值足够大,此时满足k+P<N,则开环输出满足的条件为:
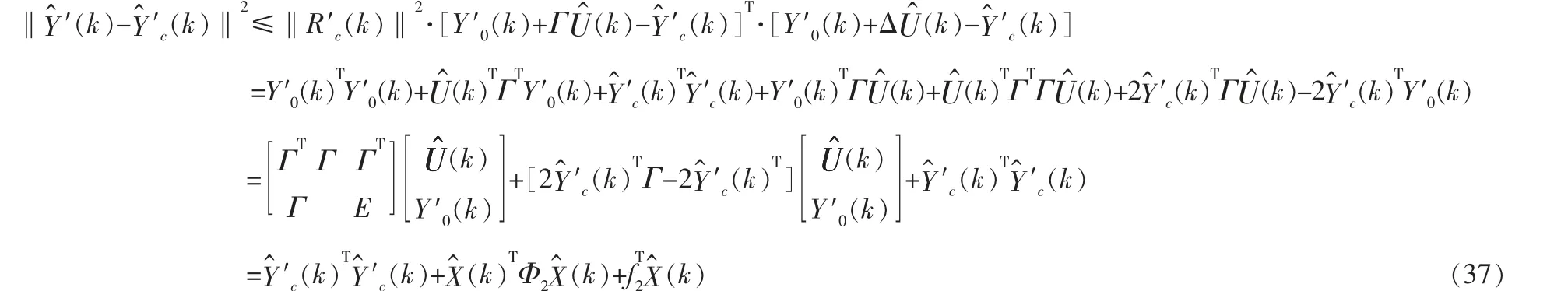

此时开环输出满足的约束可以写为:

本研究的优化问题转化为:

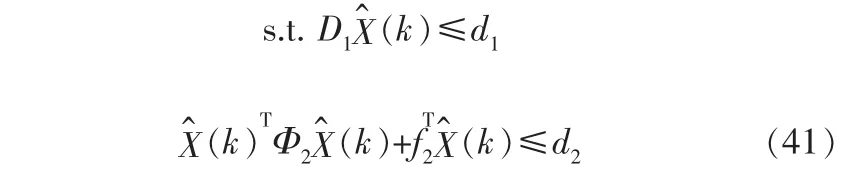
因此,渐变式椭球体区间预测控制算法转化为一个具有二次约束的二次规划问题。 采用有关算法可以获得最优解X*(k),由此得到U*(k)=[ImM0mM×rP]X*(k),k+1时刻重新滚动计算优化问题。
4 实验仿真分析
为了验证笔者所提算法在多输入多输出线性离散系统中的有效性,实验采用壳牌公司的重油分馏塔进行仿真,其传递函数矩阵为:

实验仿真结果中y1、y2、y3是输出变量,本实验仿真的系统预测时域P取25 min。 u1∈[-0.5,0.5],u2∈[-0.5,0.5],u3∈[-0.5,0.5],y1∈[-0.5,0.5],y2∈[-0.5,0.5],y3∈[-0.5,0.5], 系统各个变量表示含义以及约束条件见表1、2。 对于系统变量与约束条件均做了无量纲处理。

表1 Shell控制问题的各控制变量约束区间
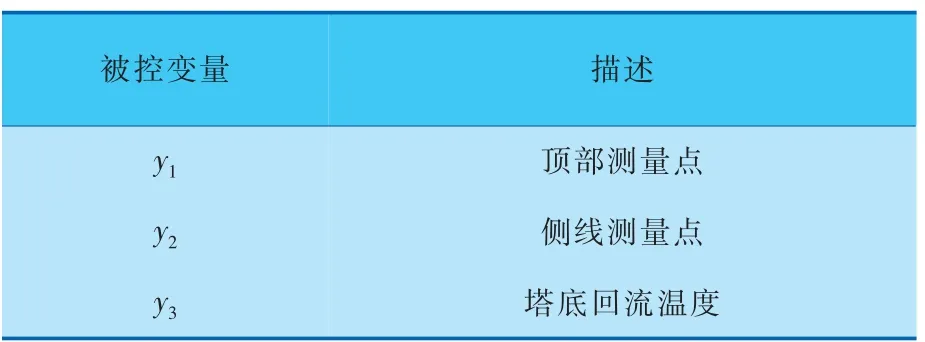
表2 Shell控制问题的各被控变量
仿真实验的预测时域P取25 min,约束序列个数N取25、50、75。 改变N值系统的控制效果不同,仿真实验重点关注N取不同值情况下, 最佳的控制效果, 即兼具响应快速性与稳定性的最佳N的取值情况。
控制目标设置为以(0.13,0.17,0.18)为球心,半径为0.1的球体区间。 N取25、50、75不同值时,系统响应曲线如图5所示。N越大系统输出进入目标区间的响应轨迹越平滑。
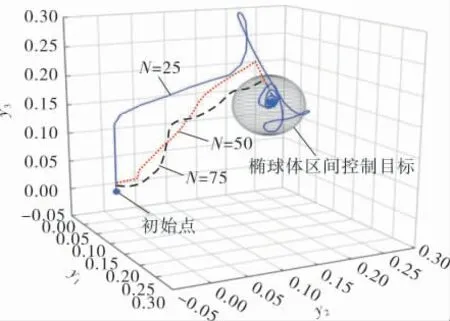
图5 系统响应轨迹
由图5可以看出,N取任何值系统输出都能最终到达目标区间,并且保持稳定。N取25时系统的响应轨迹不在约束球体序列形成的通道中,N取50时会有部分时刻的状态变量超出预设通道,当N取75时系统状态变量能完全在预设通道内部到达球体控制目标。
N取25时的仿真结果及其对应的控制律如图6所示。 此时,输出变量在进入目标区间之前产生剧烈振荡,会有大部分时刻的实际输出超出预设通道并且产生很大的超调量。

图6 N取25时系统的输出结果与系统控制律
N取50时的仿真结果及其对应的控制律如图7所示。 系统输出在进入目标区间前不会产生振荡,但仍然有部分时刻输出超出预设通道,但超调量明显变小。

图7 N取50时系统的输出结果与系统控制律
N取75时的仿真结果及其对应的控制律如图8所示。 系统输出平缓地进入目标区间并达到稳态,不会产生超调量且完全在预设通道内进入目标区间。

图8 N取75时系统的输出结果与系统控制律
用系统动态响应过程中超出预设通道的输出变量到预设通道距离的平方之和ε表示被控变量偏离预设通道的程度, 在P取25、N取值不同的情况下,y1、y2、y3的偏离程度见表3。 可以看出,在预测时域P确定的情况下,随着N取值变大,系统的控制效果会越来越稳定, 当N的取值超过50时系统输出变量能完全沿着椭球体区间的约束序列形成的通道达到稳态,不会超出通道,系统不会产生任何超调量。系统的被控变量在N取50~75之间某一确定值时能够完全在预设通道内达到目标区间。
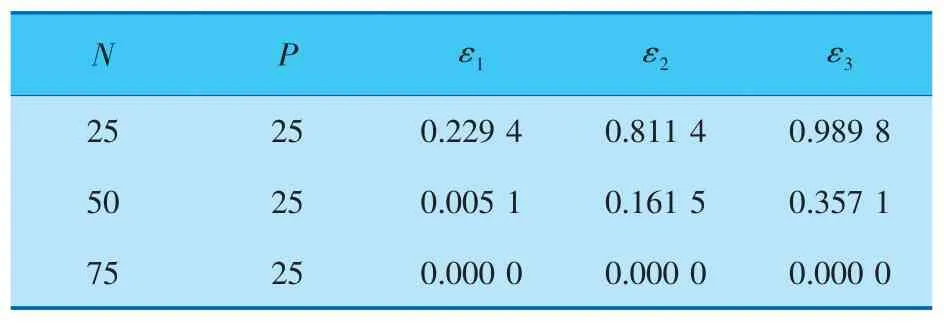
表3 输出偏离预设通道程度
为了验证笔者所提方法的有效性,将渐变式椭球体区间预测控制算法与普通区间预测控制系统输出结果进行对比,结果如图9所示。

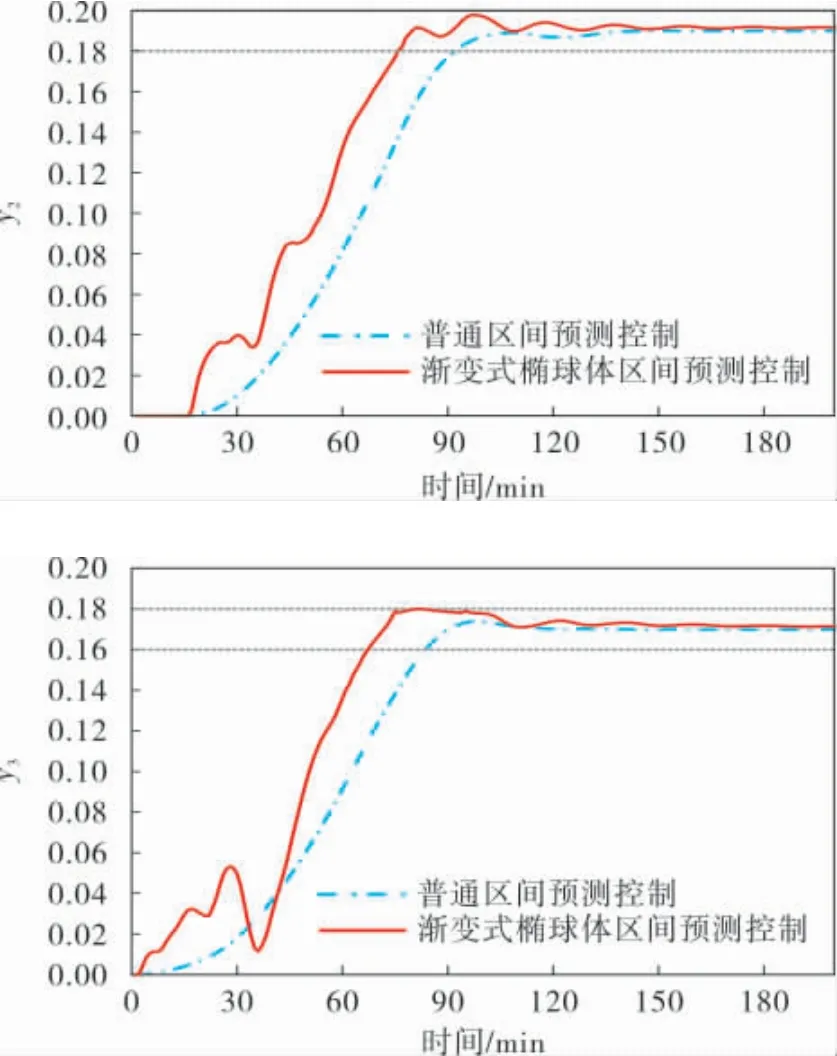
图9 两种控制方法的控制效果对比
控制目标设置为以(0.11,0.19,0.17)为球心,半径为0.1的球体区间。 仿真实验中预测时域P取40 min,球体序列约束个数N取80,在使得系统控制效果都稳定的且不产生超调量的前提下,笔者所提渐变式椭球体预测控制算法有效提高了系统的响应速度。
5 结束语
笔者在区间预测控制的框架下,提出基于渐变式椭球体区间的区间预测控制算法,该算法通过设置预设通道,使得被控变量在预设通道中进入目标区间。 同时,基于此建立相应的优化问题。在预测时域值确定的情况下,找到兼具稳定性与快速性的预设通道长度的值,使得被控变量在不超出预设通道的前提下快速进入目标区间,提高了控制的整体性能。

