仿生机器鱼的运动学建模及控制参数的优化

史晓虎，文小玲

（武汉工程大学 电气信息学院，武汉 430205）

21 世纪是海洋的世纪，仿生机器鱼融合鱼类推进机理和机器人技术，不仅具备移动灵活、速度快和适应复杂环境下工作等优势，而且还可以有效减少对环境的影响，因此在海洋领域中具有巨大的应用前景和潜在价值。

仿生机器鱼具有独特的机械结构和推进模式[1]，其运动控制是整个机器鱼的核心。 目前仿生机器鱼常用的运动控制方法主要有拟合鱼体波法、正弦控制器法和基于中枢模式发生器（CPG）的控制方法[2]。文献[3]总结了拟合鱼体波法、正弦控制器法和基于中枢模式发生器模型的控制方法的基本原理和优缺点。 文献[4]对采用拟合鱼体波控制的机器鱼的运动学模型进行了优化，有效抑制了机器鱼头部的摆动。 文献[5]从柔性机器鱼的动力学模型出发，初步探索了鱼体动力学参数与其游动性能之间的关系。文献[6]基于机器鱼的动力学模型构建CPG 网络，根据不同模态的原理设置控制参数，使CPG 网络输出不同的信号，实现机器鱼的各种运动。

在机器鱼的运动控制中，频率、幅值等控制参数的改变都会影响控制信号的输出，进而影响机器鱼的游动速度、平稳性等性能。 控制参数的整定对机器鱼的性能至关重要，却很少有人对控制参数的选择进行讨论。 本文为了合理选择频率、幅值等控制参数、使机器鱼的性能更佳，首先对采用正弦振荡器控制的仿生机器鱼进行了运动学建模和水动力学分析， 然后利用PSO 算法进行控制参数的优化，最后对机器鱼的运动学模型及控制参数优化方法进行仿真验证。

1 仿生机器鱼控制方法及运动学模型

1.1 仿生机器鱼控制方法

本文基于BCF 推进模式，设计了一种采用三关节尾鳍推进的仿生机器鱼，利用3 个舵机来控制尾鳍的摆动，从而实现机器鱼的游动，3 个舵机的摆动采用正弦控制器来控制，其机械结构如图1 所示。

图1 机器鱼结构示意图Fig.1 Schematic diagram of the structure of the robotic fish

正弦控制器法是一种基于运动学的控制方法。大多数鱼类的身体或鳍的推进波形接近正弦运动，该方法将仿生机器鱼中每个关节看作一个正弦控制器，通过改变正弦控制器的频率、幅值以及彼此之间的相位差便可产生不同的游动模态。 控制方程可以表述为

式中：φi（t）为每个关节在t 时刻的摆动角度；A 为每个关节的最大摆动幅值；ω 为频率；Ψ 为角偏移量；φ0为相邻关节间的相位滞后角。

1.2 尾鳍运动学建模

仿生机器鱼在游动的过程中，尾鳍摆动频率、幅值的变化影响着鱼类的游动性能。 本文采用正弦控制器控制机器鱼尾鳍的摆动，因此尾部关节的摆动规律为

1.3 仿生机器鱼水动力学分析

仿生机器鱼依靠尾鳍摆动进行游动，推力由尾鳍摆动伴随产生的流体推力和尾涡提供。 由于尾鳍摆动时， 尾鳍沿展向的不同位置具有不同的线速度，因此采用“微元积分”的方法对尾鳍在摆动过程中的受力情况进行分析。 如图2 所示，仿生机器鱼尾鳍分四步完成一个摆动周期。

图2 尾鳍摆动示意图Fig.2 Schematic diagram of tail fin swing

以尾鳍摆动第一步为例，分析摆动过程中的受力情况。 任取尾鳍上一微元G，其受力情况如图3所示。 图中，v0为水流相对于机器鱼沿X 方向的速度，v 为尾鳍相对来流的速度，r 为微元G 到转动轴的距离。 微元G 沿尾鳍的法向速度vn和切向速度vt分别为

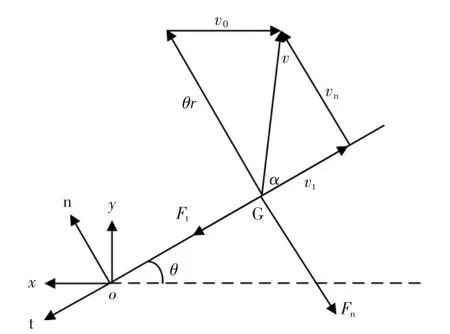
图3 尾鳍摆动示意图Fig.3 Force analysis diagram of caudal fin

尾鳍上微元G 受到周围流体沿尾鳍的法向的推力dFn和沿切向的推力dFt分别为

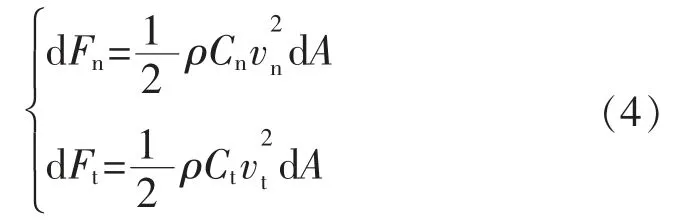
式中：ρ 为流体密度；Cn为法向升力系数；Ct为切向阻力系数；dA 为微元G 的面积。

通过力的分解与合成，尾鳍上微元G 受到周围流体的推力可等效为沿X 方向的推力dFx和沿Y方向的推力dFy。 进一步对尾鳍沿展向积分（R 为展长）， 得到尾鳍所受周围流体沿X 方向的推力Fx和沿Y 方向的推力Fy分别为

任何处于流体中的物体运动都会形成一连串尾随其后的涡流，即卡门涡街。 卡门涡街为机器鱼的游动提供了前进的推力。 卡门涡街对机器鱼的推力FSt为

式中：ω 为尾鳍的摆动频率；A 为尾鳍摆动的幅值；v为机器鱼的游动速度；k 为卡门涡街力系数。

机器鱼所受阻力主要由鱼身提供，与流体密度、流体作用与鱼身的有效面积以及机器鱼的速度有关。

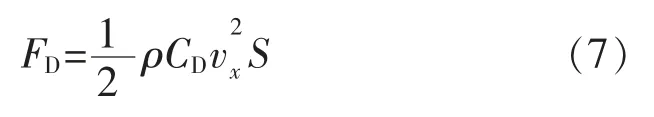
式中：FD为机器鱼受到的阻力；ρ 为流体密度；vx为机器鱼在X 方向的游动速度；CD为阻力系数；S 为机器鱼在流体中的有效作用面积。

设机器鱼质量为m，则根据上式可得机器鱼在X 方向的动力学方程为

1.4 仿生机器鱼运动学模型仿真分析

为验证所建运动学模型的有效性，对仿生机器鱼的直线游动及其性能进行了仿真分析。

机器鱼在直游时，主要考虑游动速度和平稳性这2 个性能指标。 本文中，用X 方向的平均速度表示游动速度，用Y 方向受到的最大偏转力表示机器鱼的平稳性，机器鱼所受偏转力越大、平稳性越差。

设直游状态下第一、二、三关节的摆动幅值比为1∶1.2∶1.44，摆动频率相同。 图4 为此模型直游状态下相同运动时间内平均速度和最大偏转力与尾部第一关节摆动幅值和频率的关系。

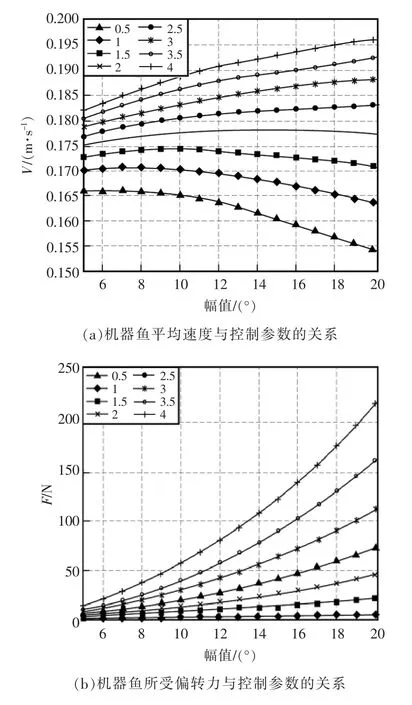
图4 直游性能与控制参数的关系Fig.4 Relationship between swimming performance and control parameters

由图4 可看出，当尾鳍摆动幅值相同时，摆动频率越大，机器鱼游动速度越大，其所受偏转力也越大，平稳性越差；当尾鳍摆动频率相同时，所受偏转力随着摆动幅值的增加逐渐增加，平稳性逐渐变差， 而速度与幅值的关系因频率的不同有所差异；当摆动频率较小时，超过一定摆幅，机器鱼游动速度随着摆动幅值的增加而减小； 当摆动频率较大时，摆动幅值越大，机器鱼游动速度越大。

2 基于PSO 的控制参数优化算法

2.1 优化函数

速度和平稳性是衡量仿生机器鱼运动状态是否最优的2 个非常重要的性能指标，并且两者会相互制约。 因此，将二者融合得到机器鱼直游控制参数的优化函数为

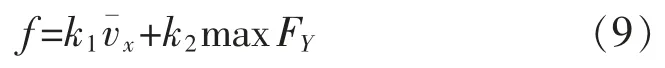
式中：k1，k2表示在优化函数中平均速度和所受偏转力FY的权重系数， 通过调节它们的大小关系，可以选择出最优控制参数，并且它们两者间的正负关系应取相反，表示两者间的相互制约关系。

2.2 PSO 参数优化算法

PSO（粒子群算法）是源自于鸟群捕食行为的一种优化算法，其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解， 具有收敛速度快、效率高等优点，因此被广泛应用到各种领域。

PSO 算法在n 维空间内进行迭代寻优，每个粒子根据当前所处的最优位置和全局最优位置来迭代更新自己的位置，每个粒子都有自己的位置向量和速度向量，以及由一个目标函数所决定的适应度值。

在每一次的迭代中，粒子都要按以下迭代算法更新自己的位置：

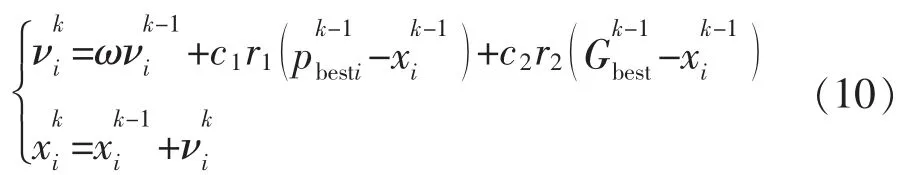
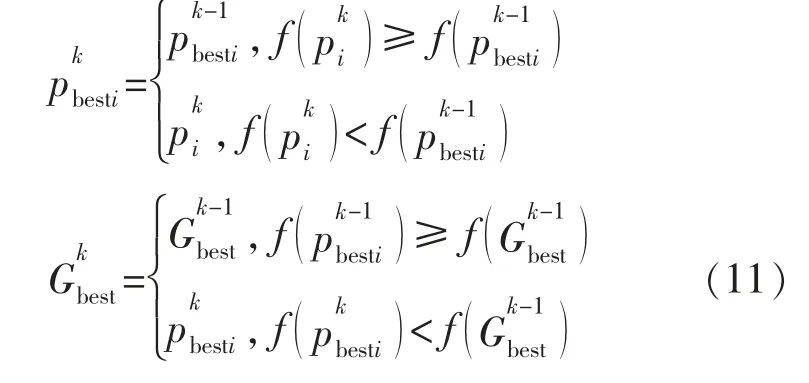
式中：f 为目标函数，通过比较不同位置的适应度值，更新最优位置。

2.3 PSO 优化算法流程

PSO 参数优化算法的流程可分为以下5 步，如图5 所示。

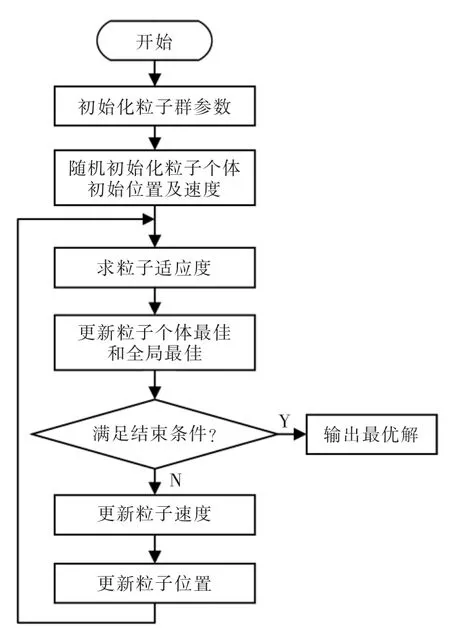
图5 PSO 优化算法流程Fig.5 Flow chart of PSO optimization algorithm

步骤1：初始化粒子群参数，设置粒子个数M、最大迭代次数N、位置界限和速度界限。

步骤2：随机初始化粒子位置以及它们各自的速度。

步骤3：计算每个粒子的适应度值，并更新每个粒子的个体最优位置以及全局最优位置。

步骤4：更新粒子速度及位置，并转到步骤3。

步骤5：判断是否达到最大迭代次数，或者达到最优解，若达到，输出最优解，否则转到步骤4。

在本文的PSO 优化算法中，直线游动状态下的粒子的位置表示为第一关节的摆动频率ω 和幅值A。

3 实验及结果分析

为了验证PSO 控制参数优化算法的有效性，基于上述运动学模型，首先随机选取机器鱼直游的两组控制参数， 然后利用PSO 算法求得了一组兼顾速度和平稳性的最优控制参数，最后对三组控制参数下机器鱼的性能进行了仿真分析。 三组控制参数的取值如表1 所示，机器鱼游动性能仿真结果如图6 所示。

图6 直游性能与控制参数的关系Fig.6 Comparison diagram of swimming performance

表1 机器鱼直游状态下的控制参数Tab.1 Control parameters of the robotic fish in the state of direct swimming

从仿真结果可以看出，对应随机控制参数1，2及PSO 优化控制参数，机器鱼的平均速度分别为0.176 m/s、0.187 m/s、0.185 m/s，最大偏转力分别为51.3 N、132.1 N、92.0 N。 仿真结果表明，采用PSO 算法进行控制参数的优化后，机器鱼既拥有较快的游动速度又具备更好的平稳性。

4 结语

为了准确控制机器鱼获得最佳游动性能，本文首先结合正弦控制器的驱动原理建立了机器鱼的运动学模型，并分析了其控制参数（频率和幅值）与机器鱼直线游动性能间的关系；然后，利用PSO 算法对运动学模型中的控制参数进行了优化； 最后，对机器鱼的直线游动进行了实验研究，实验结果表明所建立的运动学模型符合鱼类的生物学特征，并且采用PSO 算法对控制参数进行优化后，可使机器鱼的直游性能达到更佳。