基于群体压力的大群体风险应急决策方法
徐选华,刘 莹,陈晓红
(中南大学商学院,湖南 长沙 410083)
1 引 言
近年来,洪水灾害、地震、火灾及恐怖袭击等突发事件不断发生,造成了极大的人员伤亡和财产损失,阻碍了社会经济的发展,对现有的社会秩序和政府的管理造成一定的影响和冲击.突发事件是事故发生前兆特征不明显的小概率复杂事件,演化过程中影响因子较多,且事件发生后会产生高度破坏性,甚至具备潜在的二次危害[1−4].由于突发事件的不确定性和破坏性,决策专家需要在短时间内明确应急问题和决策目标并统一意见,从给定的方案中做出最优选择,减少灾害发生后的进一步损失[5−8].为了降低决策失误的可能性,通常由大规模专家群体提供他们的偏好用以共同决策.Xu等[9]提出如果群体决策中的专家数量超过11个,则认为该决策组属于大群体.然而,Liu 等[10]认为大群体决策组内专家数量应该超过20个.在大规模群体决策问题中,专家通常代表不同的利益群体,专家的社会地位、受教育程度、专业背景、专业知识结构和对决策问题的理解各不相同,从而致使群体成员间的观点产生分歧[11,12].因此,群体决策过程中会产生风险.应急决策者的局限性,灾害信息的缺失,决策环境的复杂性和动态变化性,决策的时间压力以及其他因素都会给决策造成风险[13].如果无法正确评估这些风险并加以有效控制,则会降低决策质量,甚至会产生决策失误,导致救援形势恶化.为此,Luu 等[14]提出基于多元线性回归-TOPSIS的方法,用于分析越南的灾害数据.Liang等[15]提出多粒度比例犹豫模糊语言TODIM方法,应用于针对矿山灾害的应急决策问题.Gao 等[16]使用不完整的概率语言偏好关系,提出了一种新的基于一致性的紧急决策方法,用以解决与信息的缺失和不确定性以及决策动态趋势相关的问题.Liang等[17]利用TODIM处理风险偏好特征,再将风险偏好和双重犹豫模糊三向决策结合使用.由上述研究可知,如何进一步优化对风险的度量,迄今还是一项极具挑战性的课题.为此,本文将从区间值Pythagorean模糊语言变量的使用、群体压力对偏好信息的调节、准则风险权重与准则主观权重的组合加权计算三个方面降低决策过程中的风险水平,实现对决策结果的优化.
由于应急突发事件的复杂性和人类思维的模糊性,决策者很难用清晰的数字准确地表示评估信息.因此,多准则决策分析对于决策专家而言是一项艰巨的任务.Pythagorean模糊性理论对于表示多准则决策分析问题中包含的不确定信息极为有用[18].其中,区间值Pythagorean模糊集与Atanassov的区间值直觉模糊集合具有平行关系,是Pythagorean模糊集的推广[19,20].区间值直觉模糊集和区间值Pythagorean模糊集的隶属度和非隶属度都分别设置为在[0,1]内的一个区间值.但前者隶属度和非隶属度的区间值上限总和小于或等于1[21],而后者需满足的约束条件为隶属度和非隶属度的区间值上限平方和小于或等于1[18].相较之下,区间值Pythagorean 模糊集合能表达的决策信息的范围更为广泛,也能够处理比区间值直觉模糊集更复杂的不确定性信息,因而具有更广阔的应用前景.Mohagheghi等[22]提出一个新的区间值Pythagorean模糊集框架和多目标模型,用以评估大型高科技项目组合从而解决投资组合价值最优化问题.Yu等[23]在区间值Pythagorean模糊语言环境下使用扩展TOPSIS的群体决策方法选择可持续供应商.Haktanir等[24]将区间值Pythagorean模糊集和质量功能展开方法综合应用于太阳能光伏技术的开发.Liu等[25]结合最佳最差方法(BWM),区间值Pythagorean模糊集和自组织映射(SOM)方法研究关于自助移动式回收机器的评估问题.当前,区间值Pythagorean模糊集合在其他领域已有较为丰富的研究,但在大群体决策及应急决策领域涉及较少.因此,本文将区间值Pythagorean模糊语言变量应用于大群体应急决策,旨在更进一步精确表达决策过程中的不确定性,从而减少决策风险.
应急决策不仅要求决策的时效性,也对决策准确率提出高要求以避免形势进一步恶化.决策者的心理行为能影响决策,导致决策结果的差异.然而,传统的群决策理论基于个体完全理性与追求自利的假设之上,认为主体是在认知无偏差、环境确定和信息准确的前提下做出的最优决策,但这些前提条件在突发事件环境下难以得到满足,所以会得出不合理的决策分析结果[26].随着行为科学的发展,很多学者对决策者心理行为进行研究.Carneiro等[27]认为考虑认知或者情感在某种程度上有助于决策过程.Li等[28]考虑决策者的心理行为,提出了一种基于TODIM方法的风险决策分析方法.Song 等[29]提出了考虑行为特征的正态云模型多级风险决策方法,实现对多阶段风险决策的优化.Wang 等[30]提出一种新的基于前景理论和专家的心理行为的应急群决策方法.已有研究证明,在信息不确定的环境下,群体中的个体因为存在互相间的交流与沟通,在进行决策时会彼此影响,最终导致他们做出相同或相似的决策结果,使得判断在一定程度上缺乏理性.群体压力是导致这种从众行为出现的诱发因子.当群体成员的行为与其他大多数群体成员的行为,或者与整个群体的行为不一致时,群体成员会感受到心理压力,即群体压力[31].群体压力的影响具体表现为,群体对决策问题存在一个期望决策值,当个体的决策值接近群体期望值,会得到群体成员的认可和支持,反之,当个体的决策值偏离群体期望值,则会遭到群体成员的排斥和反对,因此,群体成员有与群体保持一致的倾向.群体压力作为群决策过程中的重要影响因素,仍有待进一步的研究.为此,本文基于已有研究中关于群体压力的定义和压力效用函数的理论,定义改进的群体压力表达公式,再以接近度作为共识水平的衡量指标,以群体压力作为偏好调节系数,共同指导专家进行偏好调节.通过对偏好信息的精细化处理,从而减少决策结果的误差所带来的风险.同时,本文以专家犹豫值度量决策过程中的风险,从而调整专家给予准则的主观权重,体现专家决策的客观性越强准则权重越大这一基本原则.
综合上述研究,本文提出一种基于群体压力的风险性大群体偏好调节模型: 利用区间值Pythagorean模糊语言变量提供专家偏好信息,通过改进的群体压力模型和专家之间的接近度确定偏好调节系数,再由调整后的专家偏好集结得到新的群体偏好;构建犹豫度矩阵,通过OWA算子确定每个准则的犹豫度,从而得到准则风险权重,再与准则主观权重加权计算得到准则综合权重;通过前景理论生成前景值矩阵,与准则综合权重结合后得到每个方案的总体前景值,最后得到总体前景值最高的最佳决策方案.
2 问题描述与方法基础
2.1 问题描述
由至少20位成员组成的决策群体E={e1,e2,...,eM}进行应急决策,X={x1,x2,...,xP}表示备选方案集合;C={c1,c2,...,cN}表示为准则集合,W=(w1,w2,...,wN) 表示为准则的权重矢量,wj≥0且
为了更精准的实现对决策偏好的表达,本文将利用Pythagorean模糊语言作为表达形式.每个决策者ei给出对第l个方案的第j个准则的决策偏好表示为1,2,...,M.具体含义为:sθlji是决策者ei基于语言术语集S给出的语言评价值,其中S={s0,s1,...,sg}.分别是隶属度和非隶属度的下限值和上限值.决策大群体用Pythagorean模糊语言给出偏好矩阵,并依据群体压力进行偏好调节得到较高共识的最终群体偏好矩阵,根据前景理论处理群体偏好得到方案排序,选择总体前景值最大的最优方案.
2.2 语言变量与Pythagorean模糊集
Yager提出的Pythagorean模糊集不仅扩展了区间模糊集,还可以处理隶属度和非隶属度之和大于1的不确定性情况[32].这增强了模糊信息表达的灵活性和适用性.PFS不仅可以显示专家之间一致性的程度,还可以体现这种程度的模糊性[33,34].区间值Pythagorean模糊集合(IVPFS)通过区间而不是单个值来表示隶属度,实现了对Pythagorean模糊集的进一步改进.鉴于其具有先进性与优越性,故将使用该语言变量进行研究与分析.
假设S是包含有限个完全有序的元素的语言术语集,其中g是偶数.
定义1[35]设si ∈S为语言变量的可能值,i=0,1,...,g,则1) 如果i >j,那么si >sj;2)neg(si)>sg−i;3)如果si >sj,则max(si,sj)=si;4)如果si Xu等[36]提出的连续性语言术语集¯S={sα|s0≤sα≤sg,α ∈[0,g]}中的元素也满足上述性质. 假定X是非空有限语言集合,x是X中的元素,¯S是连续语言术语集.任意一个X中的Pythagorean模糊集(PFS)P表示为[37] 其中µP(x)∈[0,1]和νP(x)∈[0,1]分别表示X中元素x属于P的隶属度和非隶属度.同时,还满足如下条件(µP(x))2+(νP(x))2≤1. 令 称πP(x)为X中元素x属于P的犹豫度区间.P(µP(x),νP(x))是一个Pythagorean模糊数(PFN). 定义2[38]假定X是非空有限语言集合,x是X中的元素,¯S是连续语言术语集.X中的区间值Pythagorean 模糊语言变量(IVPFLV)表示为 定义3 [38]设S为语言术语集合,=〈sθ,[µL,µU],[νL,νU]〉为任意一个IVPFLN.定义的得分函数和精确函数分别为 为集结专家组的决策偏好,使用区间值Pythagorean模糊语言加权平均算子(IVPFLWA),得到的集结数值仍然是一个IVPFLN. 该部分将从基于群体压力的偏好调节模型、准则权重测定、方案排序与选择三个主要步骤展开,旨在选择面对突发事件时的最优应急方案.本文的边际贡献主要在于以下三点: 1)利用改进群体压力公式生成的压力值作为偏好调节系数,调节专家偏好和群体偏好;2)所有专家均可根据自己的偏好调节系数在偏好调节的每一轮进行动态调整,从而实时体现决策者的心理变化;3)考虑决策风险,提出犹豫度矩阵,结合OWA算子,得出准则的风险权重. 定义4[38]假设=〈sθ1,[µL1,µU1],[νL1,νU1]〉和=〈sθ2,[µL2,µU2],[νL2,νU2]〉为任意两个IVPFLNs,则˜p1和˜p2的距离定义如下 基于以往文献对区间值直觉模糊数的相似度的研究,本文根据区间值Pythagorean模糊语言变量的性质提出IVPFLNs的相似度定义. 定义5设=〈sθ1,[µL1,µU1],[ν1L,ν1U]〉和=〈sθ2,[µL2,µU2],[ν2L,ν2U]〉为任意两个IVPFLNs,=〈sg−θ2,[νL2,νU2],[µL2,µU2]〉为的补充性的IVPFLN,则和的相似度定义如下 定义6设群体偏好矩阵为各专家偏好矩阵为通过IVPFLWA算子,将所有决策者的偏好矩阵集结成的群体偏好矩阵如下 用接近度[40]衡量专家共识,设群体偏好矩阵为各专家偏好矩阵为从以下三个层次逐步计算专家对群体的接近度 1)备选方案准则间的接近程度,专家ei关于方案准则间的接近程度如下 2)备选方案间的接近程度,专家ei关于方案间的接近程度如下 3)专家与群体偏好间的接近程度,专家ei与群体的接近程度如下 文献[31]给出一个关于群体压力的非线性函数式,并认为该非线性模型更具描述性,且更贴近现实决策者的心理感受.文献[31]中将单一实数决策值作为自变量,通过决策值差值表示决策者的决策值与群体期望决策值的差距,从而得出相应的群体压力值.然而,用区间值Pythagorean模糊语言数进行决策相较于单一实数决策值能更好的表示决策者在决策过程中模糊且不确定的信息,故本文提出将基于区间值Pythagorean模糊语言数的接近度值作为自变量,用接近度差值得出相关的群体压力值来体现决策者的心理落差与压力效用.故以单一实数决策值为自变量的压力模型在本文中并不适用,需要对其进行改进.由于专家会根据群体压力调节自身偏好,故本文将群体压力值视作偏好调节系数,与群体偏好结合调节专家偏好.基于上述思路,本文将文献[31]的群体压力模型进行改进,如下 其中σi ∈[σimin,σimax],0≤H(σi)≤1.σ0为所有专家的接近度均值,视为群体共识水平.σ0为所有专家对群体的期望接近度值.若σ0的值越大,则表示专家对决策结果越为重视.反之,σ0的值越小,则表示专家对决策结果的一致性没有过高的要求.考虑到应急决策的决策结果会造成较大的社会影响,设σ0的值为0.8[41].α,β为群体压力态度系数,其中α >1,β >1.α和β越大,则表示决策专家对群体压力越敏感.θ是群体压力规避系数,即专家在同等的与对群体的期望接近度的差异下,决策专家低于期望接近度时感受到的窘迫要比专家超越期望接近度时感受到的自豪更为强烈.其中参数值采用文献[31]的实验数据值,取α=1.6,β=2.2,theta=1.8. 将群体压力值视为偏好调节系数,综合群体偏好矩阵对每个专家的个体偏好矩阵进行调节. 其中为初始专家决策偏好矩阵,为初始群体偏好矩阵,即分别为在第一次决策时给出的专家偏好矩阵和通过IVPFLWA算子集结后的大群体偏好矩阵. 到目前为止,仍没有一个标准的方法来确定共识阈值.阈值的大小通常取决于我们要处理的实际问题[42].如果决策结果极其重要,那么阈值要求就尽可能的大.但当需要专家尽快做出决策时,比如在应急决策中,则可以使用相对较小的阈值.在文献[40]中,当专家接近度满足阈值0.7时,即认为专家达成共识.故本文中设定所有专家对群体的接近度的均值不低于阈值0.7,即σp≥0.7,视为调节迭代终止的条件. 定义7设大群体偏好矩阵为对于其中任意一个犹豫区间为将其犹豫区间两端值取算术平均,构成由实数组成的犹豫度矩阵 定义8设(z1,z2,...,zn)是待聚合的犹豫值列表,OWA运算符定义为 其中ρ:{1,2,...,n}→{1,2,...,n}是置换函数.对于每个k ∈{1,2,...,n−1},存在zρ(k)≥zρ(k+1). 定义9[43]比例模糊量词Q可视作在单位区间[0,1]上的模糊子集.对于任意y ∈[0,1],µQ(y)表示比例y与量词Q的含义相容程度.具有隶属函数的非递减比例模糊量词表示为 其中a、b、y ∈[0,1].同时,满足属性: 当y1>y2时,µQ(y1)≥µQ(y2).参数a=0,b=1. 在选定的比例模糊量词基础上,维度为n的OWA运算符的权重计算如下[43] 利用OWA运算符,计算犹豫度矩阵πc=[πlj]p×n中第j个准则的犹豫值 将每个准则的犹豫值进行归一化,得出第j个准则的风险权重 假设专家给予准则的主观权重已知为wsj,通过组合加权方法,计算准则权重为 其中φ为主观权重在进行加权处理时的权重系数,0≤φ≤1.φ值越大,专家给予准则的主观权重在准则权重中占比也就越大.专家决策风险越大时,专家给出的准则权重也应越低.在此处,将风险权重作为客观权重,用以调节专家给予准则的主观权重.φ的值设定为0.5[39]. 前景理论是在具有决策风险的前提下决策者的行为描述模型,可以用前景值来表示对方案的偏好程度. 定义10[39]设∆xi=xi−x0为现有前景值与决策者的心理平衡点之间的偏差程度,x0为决策参考点.∆xi≥0 表示增益,∆xi <0表示损失.前景值函数通常为 其中α是与增益相关的凹度参数,β是与损失相关的凸度参数,0≤α≤1,0≤β≤1.α和β的值越大,决策者的决策风险就越大.θ(θ >1)表示决策者的风险规避程度.θ的值越大,决策者的风险规避程度就越大.根据文献[39]的实验结果,α和β均取值为0.88、θ的值取2.25. 假设r0为决策者的心理参考点,r0的值设为1.65[39].在和r0之间可能存在三种情况,∆为正面前景偏差值与负面前景偏差值之和.正负前景偏差值可根据表1进行计算[39]. 表1 三种可能情况下的前景偏差值Table 1 Prospect deviation value for three possible situations 其中ν∗=max{|νlj|}. 计算每个方案的总体前景值如下 所有方案都可以按照总体前景值降序排列,具有最大总体前景值的方案为最优方案. 为验证本文方法的实用性和可行性,以“8·12”天津滨海新区爆炸事故这一特大突发事件为例进行分析.2015年8月12日,位于天津滨海新区塘沽开发区的瑞海国际物流有限公司所属危险品仓库发生爆炸.爆炸位置为滨海新区第五大街与跃进路交叉口的一处集装箱码头,引起爆炸发生的是集装箱内的易燃易爆物品.23时34分,在爆炸现场的数十米高空瞬间腾起灰白色蘑菇云.随后爆炸点上空被火光染红,现场附近火焰四溅.现场接连发生爆炸,导致人员伤亡惨重.事故发生第一时间,就引发广大群众的密切关注,众多网络用户在短时间内通过社交媒体实时发表自己的看法与见解.党组织高度重视,迅速成立天津市应急决策指挥中心,全方位开展救援以及善后处理各项工作.应急指挥部紧急召集了消防、化工、环保等领域的20位应急管理专家组成决策专家大群体对爆炸事故现场进行综合评估,同时根据火灾情况制定了如下4个应急备选方案: x1: 调集消防员和消防车等专业装备赶赴救援全力灭火,冷却隔离起火区域;派遣防化人员赶赴现场配合消防员网格式搜救被困伤员;将距离事故核心区范围三公里内的居民全部撤离;组织医药物资,派遣医疗专家协助开展医疗救援工作;调派无人机,绘制现场360度全景图;设立环境监测点,监测空气质量和环境污染. x2: 调集消防车、消防员赶赴救援全力灭火,冷却隔离起火区域;派遣防化人员赶赴现场配合消防员网格式搜救被困伤员;疏散附近小区居民,发放救援物资,设置居民安置点安排住宿;组织医药物资,增派医生、护士等医护人员,开展献血工作;对现场航拍勘测,详细勘测各隐患起火点;设立环境监测点,监测空气质量和环境污染. x3: 暂缓大规模灭火,派遣防化人员携带专业装备进入事故核心现场搜救;将距离事故核心区范围三公里内的居民全部撤离;组织医药物资,派遣医疗专家协助开展医疗救援工作;调派无人机,绘制现场360度全景图;设立环境监测点,监测空气质量和环境污染. x4: 暂缓大规模灭火,派遣防化人员携带专业装备进入事故核心现场搜救;疏散附近小区居民,发放救援物资,设置居民安置点安排住宿;组织医药物资,增派医生、护士等医护人员,开展献血工作;对现场航拍勘测,详细勘测各隐患起火点;设立环境监测点,监测空气质量和环境污染. 在进行方案选择前需要提前制定评价准则.因此,决策专家根据以往对类似突发事件的处理经验交流探讨出五个方面因素作为方案的评价准则:灾情控制程度c1、人员伤亡控制程度c2、人力资源消耗c3.其中,c1和c2为收益准则,c3为损失准则.决策专家大群体使用粒度为7的语言术语集S给出决策偏好信息.其中,s0=非常差,s1=差,s2=稍差,s3=一般,s4=稍好,s5=好,s6=非常好. 考虑专家在决策过程中所面临的群体压力,利用改进的群体压力公式得到偏好调节系数并进行偏好调节.由于专家在决策中的犹豫程度会造成决策风险,所以本文将专家的犹豫度矩阵与OWA算子结合运算确定风险权重,用以调节准则主观权重.为了达到较高的群体共识水平,专家的偏好调节过程将进行几轮迭代直至满足接近度阈值,从而得到理想的决策方案. 步骤1基于群体压力的专家偏好调节.决策专家以区间值Pythagorean模糊语言数的形式对四个方案的三个准则分别给出决策偏好信息,每个专家的决策偏好矩阵如表2所示. 表2 专家决策矩阵Table 2 Expert decision matrix 利用式(7)至式(12),可以得到群体偏好矩阵和每个专家对群体偏好的接近度列表,如表3和表4所示. 表3 群体偏好矩阵Table 3 Group preference matrix 表4 专家对群体的接近度Table 4 Proximity degree of experts to the group 由表4可知,所有专家对群体的接近度均值并未满足阈值0.7,故需要对专家偏好进行调节.由于专家会根据所处的群体压力对自身偏好进行调整,故利用公式(13)求得每个专家在当前的群体压力值,即获取偏好调节系数列表,如表5所示. 表5 专家的偏好调节系数Table 5 Experts’preference adjustment coefficient 利用式(14),得到第一轮偏好调节后的专家决策矩阵,如表6所示. 表6 第一轮偏好调节后的专家决策矩阵Table 6 Expert decision matrix after the first round of preference adjustment 利用式(7)至式(12),可以得到群体偏好矩阵和每个专家对群体偏好的接近度列表,如表7和表8所示. 表7 第一轮偏好调节后的群体偏好矩阵Table 7 Group preference matrix after the first round of preference adjustment 表8 第一轮偏好调节后的专家对群体的接近度Table 8 Proximity degree of experts to the group after the first round of preference adjustment 由表8可知,所有专家对群体的接近度均值并未满足阈值0.7,故需要再次对专家偏好进行调节.由羊群效应可知专家会对自身偏好进行调整,故利用式(13)求得每个专家在第一轮偏好调节后的偏好调节系数列表,如表9所示. 利用式(14),得到第二轮偏好调节后的专家决策矩阵,如表10所示. 利用式(7)至式(12),可以得到群体偏好矩阵和每个专家对群体偏好的接近度列表,如表11和表12所示. 表11 第二轮偏好调节后的群体偏好矩阵Table 11 Group preference matrix after the second round of preference adjustment 表12 第二轮偏好调节后的专家对群体的接近度Table 12 Proximity degree of experts to the group after the second round of preference adjustment 由表8可知,所有专家对群体的接近度均值满足阈值0.7,故不再需要对专家偏好进行调节,即迭代终止.此时求得的群体偏好矩阵即为满足阈值条件的最优偏好矩阵.利用式(15),得到标准化后的群体偏好矩阵,如表13所示. 表13 标准化群体偏好矩阵Table 13 Standardized group preference matrix 利用式(16),得到区间值群体评价矩阵,如表14所示. 表14 区间值群体评价矩阵Table 14 Interval-valued group evaluation matrix 步骤2计算准则的权重.利用式(17),计算得到专家的犹豫度矩阵,如表15所示. 表15 专家犹豫度矩阵Table 15 The matrix of experts’hesitation degree 利用式(18)至式(22),求得准则的风险权重为wr=(0.329,0.334,0.337).假设专家给予准则的主观权重已知为ws=(0.3,0.5,0.2),利用式(23)的组合加权方法,计算得到准则权重为w=(0.318,0.417,0.266). 步骤3方案排序与选择.为了保证总体前景值的取值范围在0和1之间,需要利用式(24)至式(25),得到归一化的前景值矩阵,如表16所示. 表16 归一化的前景值矩阵Table 16 Normalized prospect value matrix 由于本文主要在文献[39]的方法的基础上进行了改进与创新,为了证明文章所提方法的先进性,特将本文的方法与文献[39]的方法进行对比,分析两者方案排序的差异,如表17所示. 表17 不同方法下的方案排序对比Table 17 Comparison of schemes’rankings under different methods 本文方法与文献[39]的方法在最优方案选择上有所差异,原因如下: 在爆炸事故发生后,居民安置问题成为政府关注的重点,救援物资的发放和安置点的设立可以有效安抚居民情绪,减少群众恐慌.为了尽可能减少人员伤亡,不仅需要增派医护人员,还要组织献血工作,及时补充血库.同时,航拍勘测隐患起火点可以有效控制灾情进一步发展的可能,避免再次出现人员伤亡,还可以减少人力资源消耗. 本文以专家偏好对群体偏好的接近度值作为共识水平,并以其为衡量指标,将本文方法与文献[39]的方法进行对比.对比结果如表18所示. 表18 不同方法下共识水平对比Table 18 Comparison of consensus levels under different methods 综上,本文相对于文献[39],有以下三个优势: 1)本文的方法在专家偏好调节后的最终共识达成,共识水平的程度比文献[39]的程度要高,这意味着本文的方法可以更好的达成群体共识;2)实现对所有专家偏好的动态调节,而文献[39]不存在偏好调节以达成共识的过程,偏好调节过程的缺失会在一定程度上降低决策的科学性与准确性,可能会造成决策实施后的进一步损失;3)考虑了专家决策过程中的犹豫程度这一风险,用来调节专家给予准则的主观权重,这一观点充分体现了专家偏好的不确定性越低则权重越大的原则,在方法上更具客观性和合理性.本文考虑了行为科学中的羊群效应,通过改进的群体压力模型得到偏好调节系数,使得在决策过程中的专家偏好以及对群体的接近度能够有效显示专家决策过程的心理变化,并从风险的角度进行权重修改,从而更好地调节大群体决策共识. 本文在对大群体决策中决策风险和群体压力的特点进行分析后,提出了基于改进的群体压力模型的大群体风险应急决策偏好调节方法,主要创新点为以下三个方面: (1)将决策专家所面临的群体压力纳入偏好调节的考量范围,从而更好地达成共识;(2) 所有决策专家可根据自身的实际心理行为对偏好进行动态调整;(3)依据准则偏好的不确定性度量决策风险,因而准则权重更具客观性. 将群体压力与公众意见结合到大群体应急决策中,还有许多问题值得探讨,如公众意见对决策的影响、专家分时段的偏好调整、专家偏好的调整成本控制、专家聚类方法以及群体压力的风险规避系数变化等问题,未来的研究将对此进一步拓展与深化.2.3 区间值Pythagorean模糊语言变量
3 基于改进群体压力模型的专家偏好调节
3.1 专家偏好接近度测度
3.2 群体压力模型改进
3.3 专家偏好调节模型
4 准则权重测度与方案排序
4.1 犹豫度矩阵与准则风险权重的计算
4.2 组合加权确定准则权重
4.3 基于前景理论的方案排序

5 案例分析与方法对比
5.1 案例背景及问题分析
5.2 方法应用过程












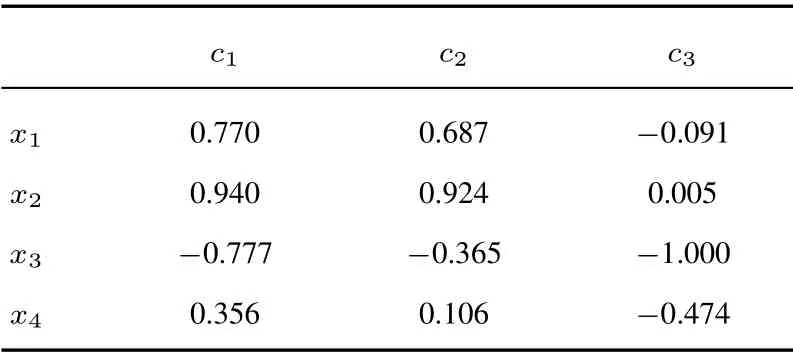
5.3 对比分析


6 结束语

