基于加权L1 范数最小化算法的地震数据重建方法研究

梁 爽，武召祺，彭 清

(东华理工大学，江西 南昌 330013)

引言

自工业革命开始，化石能源日益成为社会经济发展的动力源泉，并为人类的生存和发展提供了坚实的物质基础，同时经济发展也会进一步促进能源的勘探、开采和利用，可见社会经济发展和化石能源之间有着密切关联。目前，我国经济正处于快速发展阶段，对煤、石油、天然气等资源需求量不断增大，资源勘探也就成了经济发展的重中之重[1]。地震勘探可以利用人工激发的地震波获取地下矿藏信息，是一种高效的油气勘探方法，在资源勘探当中被广泛应用，为我国煤炭、石油等行业发展做出了巨大贡献。

基于大部分信号具有稀疏性的特点，2004 年Donoho 提出压缩感知理论将地震数据重建问题转化为简单的去噪问题，实现利用较少采集数据获得近似完整的地震勘探效果[2]。该理论具有采样速度快、存储空间小、经济成本低的优点[3]。重建算法是压缩感知理论的核心问题，通常将压缩感知理论重建算法分为3大类：第一类为贪婪算法，包括匹配追踪算法、正交匹配追踪算法等；第二类为组合算法，包括傅立叶采样、链式追踪及HHS 追踪等；第三类为凸优化算法，包括域值迭代法、投影梯度算法等[4-5]。L1 范数谱投影梯度算法具有操作简单、适用处理海量数据的特点。但该方法在数据重建过程中相邻切片是独立重建的，忽略了地震数据有效波具有连续性的特点，为此本研究提出一种基于加权L1 范数最小化算法的地震数据重建方法，该方法以压缩感知理论为基础，以曲波变换为稀疏基，用不同时间切片有效波曲波系数的相关性作为先验信息，从而提出加权L1 范数约束条件，选取相邻切片的有效数据进行重建，使重建后的地震数据同相轴更为连续，在实现高精度地震数据重建同时也进一步提升抗噪能力。将本研究方法应用于处理实际野外采集数据，实验结果验证了本研究提出方法的实用性与有效性。

1 数据重建原理

1.1 压缩感知理论

压缩感知原理充分利用信号具有稀疏性的特点，解决了尼奎斯特理论采样频率必须大于信号最高频率2 倍的要求，仅用少量数据就可以恢复出近似完整原始数据f⊂RN。

式中，ψ 为随机采样矩阵，y∊R M(M≪N)为缺失数据，因此在 ψ和y 已知的前提条件下，可以通过地震数据重建恢复出近似完整的地震数据f。由于地震数据在时间域内不具有稀疏性，本研究以曲波变换φ为稀疏基，使f 在变换域 φ内进行稀疏表示，则

式中，α 为稀疏系数，H 为共轭转置矩阵，则公式（1）可写为

当 ψ满足限制等距特性时，可以通过L1 范数最小化算法不断促进求解最优稀疏系数，即

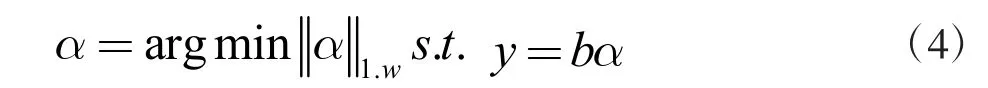
1.2 加权L1 范数最小化算法

地震数据的物理属性具有连续性，因此可以对地震数据进行加窗处理，把地震数据转化成时间切片，利用相邻切片之间的高度相关性促进稀疏系数α 的恢复，但标准L1 范数最小化方法并没有考虑到这种情况，因此本研究用加权L1 范数最小化算法代替标准L1 范数最小化，将公式（4）改为：

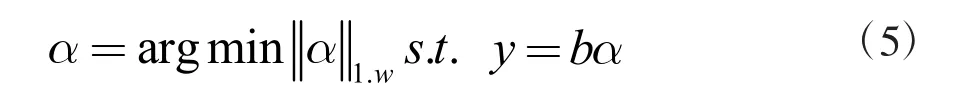
经过实测分析，当γ=0.3 时加权L1 范数最小化算法重建后信噪比值最大，重建效果最佳，因此在后续实验当中参数γ 均取值为0.3。

2 实测数据处理

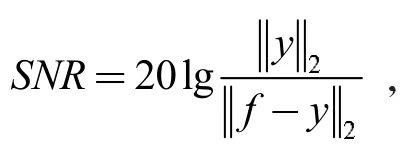
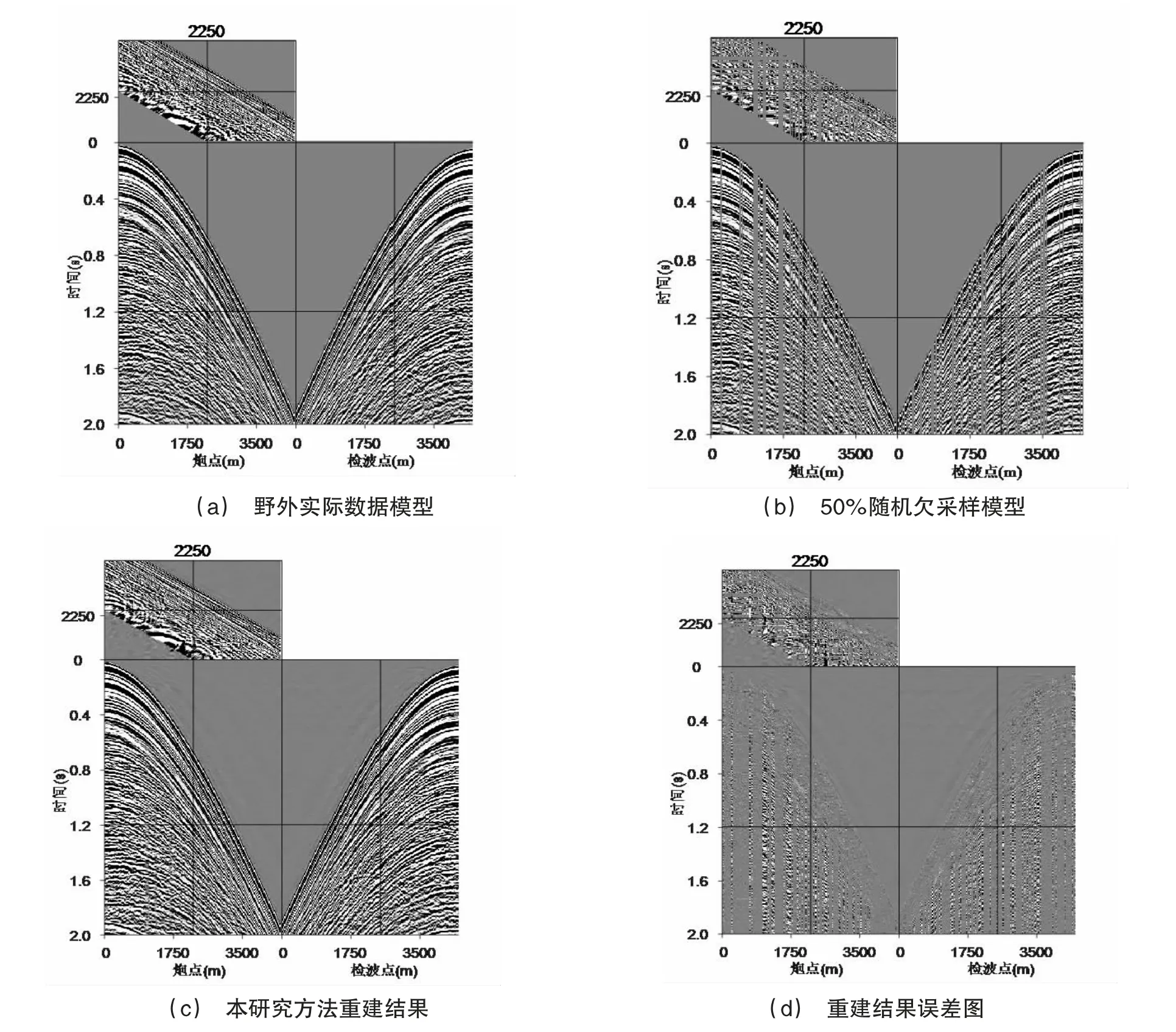
图1 野外地震数据模型及重建结果

为进一步验证文本方法兼具实用性与有效性，还采用标准L1 范数最小化算法对50%随机缺失数据进行重建，两种算法在不同迭代次数下的信噪比关系图见图2，由图2 可知，起初随着迭代次数增加，两种算法重建后信噪比均有效增长，但当迭代次数超出某一数值后，信噪比数值将趋于稳定，此时加权L1 范数最小化算法的重建结果要明显优于标准L1 范数最小化算法。综上所述可以得出，在处理野外实际数据中，本研究方法可以实现高精度的地震数据重建。

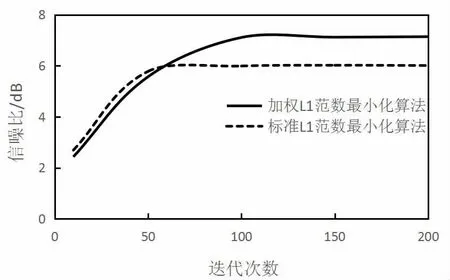
图2 不同迭代次数与信噪比关系曲线图

3 结论

（1） 为了提高地震数据重建精度，本研究在标准L1 范数最小化算法的基础上，依据地震数据有效波具有连续性的特点，提出加权L1 范数最小化重建算法。对比这两种算法可以得出，本研究方法重建后信噪比数值更大，重建效果更佳。

（2） 实验结果表明，对于处理野外采集的缺失地震数据，本研究方法具有重建误差小，鲁棒性好和抗噪能力强的优点。因此资金成本，重建精度这两方面方面考虑，本研究所提出的方法具有可行性和实用性。