运动想象与其子过程相关脑电特征的数学分解和融合*
袁密桁,吕晓彤,董煜阳
(昆明理工大学 信息工程与自动化学院,云南 昆明 650504)
0 引言
脑机接口(Brain-Computer Interface,BCI)是一种变革性的人机交互[1],其中基于运动想象(Motor Imagery,MI)的BCI 是一类重要的脑机交互,其在运动意图的控制和运动功能障碍康复中具有潜在的应用。现有的MI-BCI 系统主要致力于解码MI 涉及的肢体类型(Types of limbs)并映射为特定的控制指令[2-3],以实现大脑的感觉运动意图直接、自然地与外部环境进行所需要的交互,如可以通过MI-BCI 系统将腿部的运动意图转化为驱动外骨骼机器人的指令,以实现对下肢瘫痪患者的康复训练[4]。
然而,迄今为止的MI-BCI 研究大多将MI 作为一个整体活动来理解,仅识别其所涉及的肢体,少有将MI 分解为若干子过程(sub-process/subprocedure)来解码[5],如图1 所示。由于没有解码MI 的子过程,不能反映真实的运动意图,也难以实现较精细、高维和准确的控制。

图1 目前MI-BCI 系统的肢体识别过程
实际上,MI 是一种包含若干子过程的心理活动,例如,想象右手臂举起和放下运动,可以分解为首先想象手臂从自然下垂状态举起到齐肩的水平位置,其次想象从水平位置举起到垂直向上的位置,再次想象从垂直向上的位置下放到水平位置,最后想象从水平位置回到自然下垂状态。MI 要求用户或被试者在心里逼真或生动地重复或排练相应的实际运动过程(包含若干子过程),其所需的时间必须与相应实际运动所需的时间一致[6],并要求参与者心理体现或心理感受/体验出实际运动的各个子过程,避免草率或者应付式地瞬间完成[7]。用户或被试者通过一定量的MI 训练,能够可控地或可操作地执行MI 过程[8],如图2 所示。

图2 MI 识别子流程
本研究针对抓握物体的MI 过程,将该过程分解为打开手掌(opening hand)和抓握(gripping hand)想象两个子过程,被试者在执行想象的抓握物体时,要求其逼真、可控地想象两个子过程。由于这两个子过程不相同,相应的大脑控制指令和过程也不相同,因此,假定两个子过程相关联的脑电(Electroencephalogram,EEG)特征也不相同,并能够区分。为验证该假设,建立MI 与其子过程相关EEG 特征的数学模型,然后选择EEG 通道构建静息态特征空间作为参考,并表征MI 及其子过程的EEG 特征,最后求解MI 与其子过程EEG 特征之间的关系,证明MI 分解和融合的可能性。本研究有望为MI-BCI 系统精细、高维和准确地控制提供新思路。
1 材料和方法
1.1 MI 与其子过程EEG 特征关系的数学模型
引言中所述命题可以理解为,对于某一运动想象脑意图(记为a,对应的EEG 数据记为A),均可以视其为特定子意图(记为b,c,d,…,对应的EEG 数据为B,C,D,…)的一个累加态,因此,引言中命题的数学表示为:

式中:Af,Bf,Cf,Df,…为对应的EEG 数据A,B,C,D,…映射到特征空间的特征;F(·)Fusion为特征融合方法;m为相关性矩阵。
不失一般性,为了方便实验验证和数学分析,本研究将a对应的子意图简化为b和c这两个,式(1)可简化为:

式中:A´f=F(Bf,Cf)Fusion。进一步验证该数学关系对于同一被试者具有统一性,则式(2)可表示为:

1.2 实验设计及实验过程
1.2.1 实验设计
将一个连续的运动想象过程分解为若干个子过程是一件较为困难的事情,但站在验证命题的角度,实验范式只需满足命题要求,即运动想象动作a 为子动作b 和c 的累加即可。如图3 所示,将a 定义为右手手掌摊开,再从摊开到握拳的想象过程;b的运动想象内容定义为右手手掌摊开的运动想象过程;将c 定义为右手手掌握拳的运动想象过程。

图3 3 组运动想象a、b、c 的实验内容
1.2.2 实验过程
如图4 所示,本文选取15 名身体情况健康的右利手为被试者,实验中被试者坐在提示屏幕正前方,面部距离显示屏约75 cm,认真按照实验刺激程序的流程进行运动想象。本实验所选择的实验设备型号为64 通道的Cognionics 无线干电极脑电采集设备,电极安放依据64 导联的国际标准,所有导联均采用AgCl 电极,各电极的阻抗均通过Cognionics Acquisition Beta 软件设置被降至5 kΩ以下,初始采样频率设置为500 Hz,设备的带通滤波设置为0.5~40 Hz,参考电极为左侧和右侧的耳后隆起位置[9-10]。

图4 实验过程
实验开始前,被试者需在静息态下采集1 min的EEG 作为对照组。实验开始时,实验范式提示端的显示器背景先为黑色,接着开始显示指导语持续2 s,帮助被试者理解实验内容;然后出现黑底白色的十字光标2 s 作为准备阶段,第4 s 时出现运动想象内容的提示图片和文字,被试者观察提示内容2 s 后,提示屏幕上再度出现十字光标2 s,然后黑屏进入4 s 的运动想象过程,随后再出现十字光标2 s 作为被试者的休息时间,再进入下一次运动想象。被试者单次实验的累计运动想象次数为30次,每次实验间被试者休息2 s,运动想象a、b 和c 共计90 次,获得数据集A,B和C各30 组。以运动想象c 的实验为例,具体的实验流程和对应的实验范式的刺激程序如图5 所示。

图5 实验范式流程c
1.3 实验数据分析方法
1.3.1 特征提取算法选择和通道选择
(1)基于静息态参考和Frobenius范数(Frobenius-Resting state,F-Rs)的特征向量表达
式(1)要求将可以表征运动想象意图的矩阵空间的数据投射到特征空间,这个投射过程所采取的特征提取方法在本研究中是非常重要的。与传统的脑电分类研究不同,这里所规划的特征提取算法并非以分类效果为指标,而是该特征能够尽可能全面而准确地表达需要表征的运动想象意图。
在不考虑数据的相容性的情况下,EEG 信号的每个通道的数据都可以作为一个高维向量Zi,同时也可以视为一个矩阵。而对于一个向量的充分表征,当然可以从相对某一参考的模长与夹角进行描述。对于一个矩阵的描述,可以从范数的角度进行理解。这里定义静息态EEG 为Rs作为参考静息态EEG 的模长作为单位模长,将运动想象的EEG 信号从笛卡尔空间变换到静息态空间[11],如图6 所示。

图6 基于静止状态参考和Frobenius 范数的特征向量表示
Frobenius 范数是指对矩阵全部元素平方和的平方根,即:

当矩阵为一维时,Frobenius 范数求解得到的即为模长,而且从矩阵的角度来说,Frobenius 范数对矩阵任一元素的概括均是遍历的。下面本文根据N维向量的夹角公式得到Zi与Rs的余弦相似度[12],计算公式为:

接着通过坐标变换,任一通道的EEG 均可表征为:
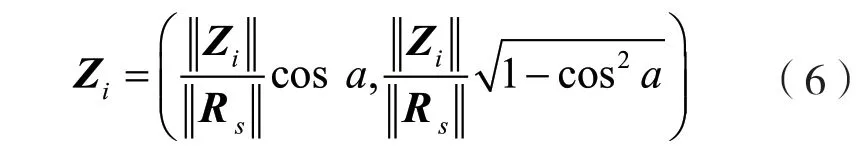
(2)基于EEG-MI 的通道贡献的导联选择
据现有研究,运动想象EEG 的采集主要使用C3、Cz和C4三个通道及其附近通道[13]。在本研究中,笔者希望可以尽可能地选择合适的通道的数据去表达运动想象的内容,因此需要研究各个导联组合对运动想象的贡献程度。这一基本思路是利用1.2.1节中描述的方法去提取各个通道的特征,再通过无监督的聚类算法去做简单的运动想象的二分类,按照分类的精度去寻找最合适的导联组合。
为避免不必要的讨论,本文首先在C3、Cz 和C4 三个通道及其附近选取共计13 个通道作为组合的基底,如表1 所示;其次按照空间位置规划了多种通道组合,如图7 所示,并采用无监督的K-means算法[14]去分类这些通道组合下的运动想象数据;最后利用分类准确度去标定各个组合对运动想象的贡献。

表1 所选取的通道

图7 各通道组合
1.3.2 运动想象子过程的特征融合
按式(1)所述,需要对Bf和Cf进行特征融合,典型的特征融合算法包括串联融合、并行融合和典型相关性分析(Canonical Correlation Analysis,CCA)[15],这些算法有其各自的优势并在自己的领域可进一步拓展算法的功能,如串联融合可以延伸为结合网络训练的加权串联融合;CCA 可拓展为mCCA 以解决多变量的典型相关性问题,或引入核函数(Kernel Function)的概念将CCA 增强至kCCA,以解决变量间的非线性典型相关性[16-17]。而本文需要融合的特征为一组二维样本,同时Af的对应的运动想象过程为Bf和Cf的一个顺序连接的过程,因此,最直接的思路是,直接利用样本层的融合,直接得到A´f,即Af中的每个样本由Bf和Cf对应位置的样本加权融合而成。
则式(2)的串联融合表达式为:

式中:α和β为融合权值。则式(2)中m可以表示为:

则式(7)的求解即为:
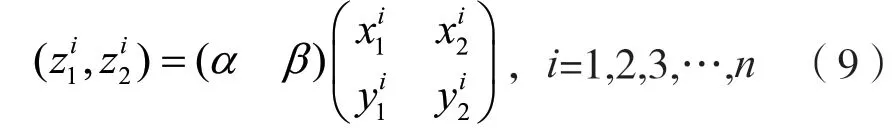
即可求解出αi和βi,进而得到mi,取其中一个被试者的结果。
此外,考虑到本研究下的特征现实语义是表达Bf和Cf对组成Af的贡献度,因此尝试从每个特征的特征进行融合,即融合子特征和组合特征的对应样本点建立数学关系,则其表达式为:
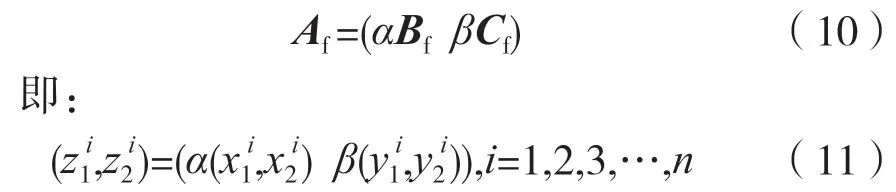
同理,可求解出m。
2 实验结果
使用各类通道的分类结果如表2 与图8 所示,其中表2说明了各组通道组合方式所选取的通道数。根据第2 组的测试结果可知,单纯的C3、Cz 和C4三个通道在本研究的实践中并不能很好地反映运动想象的语义;但是根据第3 组结果对比可知,C3、Cz 和C4 三个通道对于运动想象的表征是必不可少的。最后根据9 组的结果对比,可以确定第6 组的导联组合下的信号对运动想象的贡献最多,因此,在后续研究中选择第6 组的9 通道导联组合。
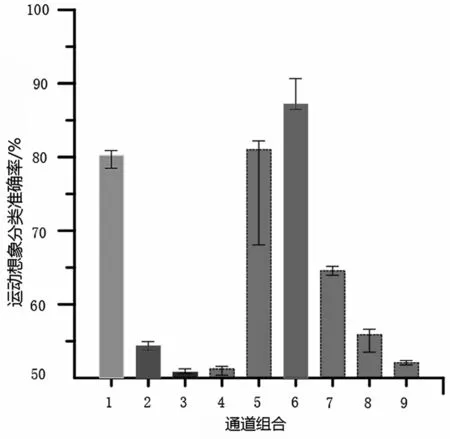
图8 不同通道组合的运动想象数据分类结果

表2 所选取的通道
通过通道选择和基于F-Rs 特征提取后,在静息态空间内12 组被试者的Af,Bf和Cf的空间分布如图9 所示。组合特征与两个子特征均属于同侧肢体的运动想象,且反映的是手部的精细姿态——摊手和握拳,但在特征空间内,三类特征在不依赖任何训练模型和分类算法的情况下,各个特征依然表现出比较明显的聚集性。这证明经过上述数据处理过程得到的三类运动想象特征Af,Bf和Cf符合理论预期。
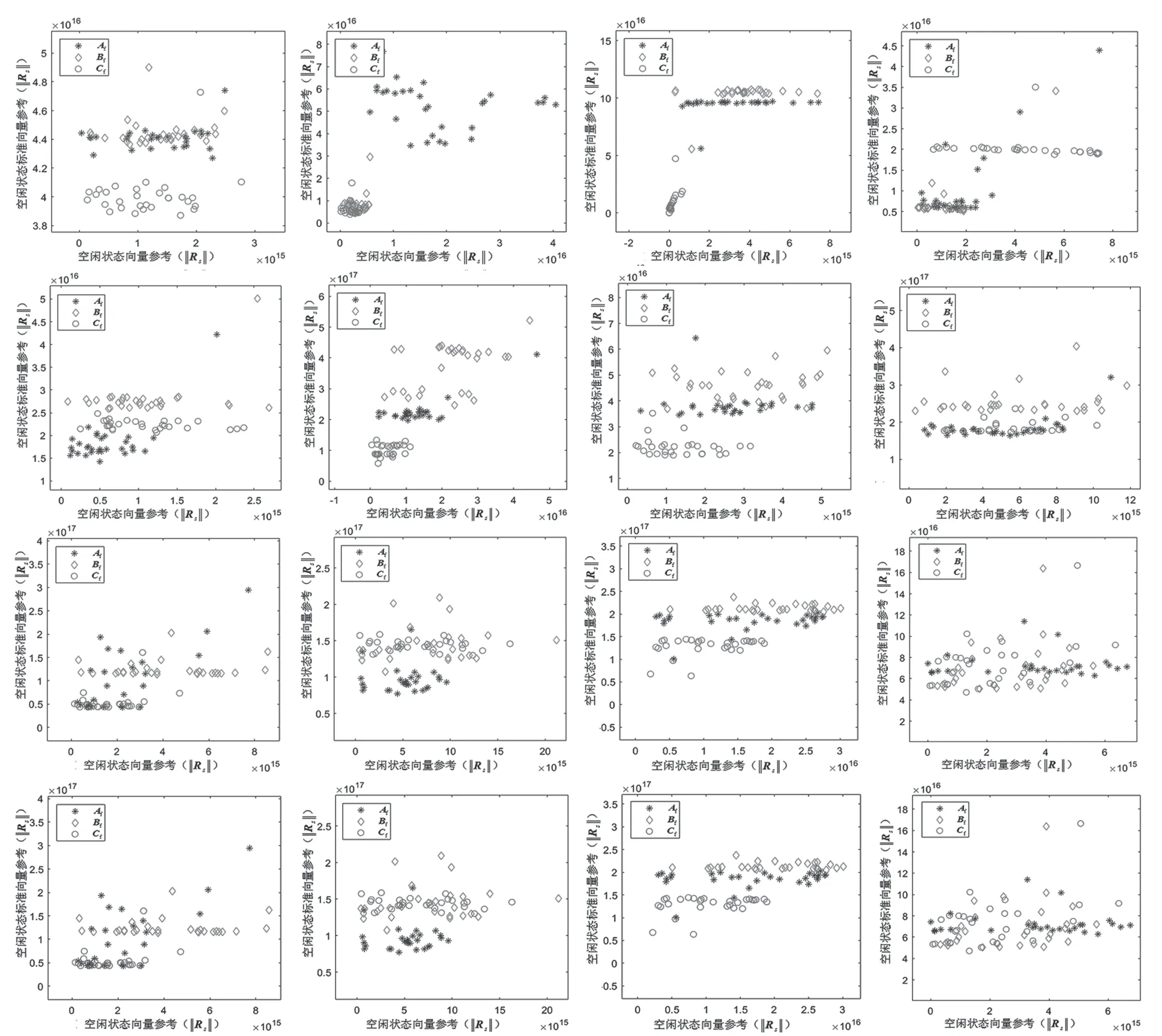
图9 静态空间内Af,Bf 和Cf 的空间分布
运用上述特征融合可求解出m,如图10 所示。进一步的,对两种融合方式下的mi找到聚类中心m^,利用m^,Bf和Cf计算AF特征,最后对比AF和Af特征,对比结果见图11。可以看到,利用串联融合求解的m可以较好地拟合运动想象子特征与运动想象特征,但从特征样本的对应关系来入手,反而不能拟合出较好的结果。

图10 两种特征融合方法求解融合矩阵m 的结果分布

图11 基于两个融合矩阵m 在静息状态参考空间中的融合特征分布
3 结语
本研究首先将问题转化为一个数学解的判定问题,其次设计了符合数学命题的单侧肢体的运动想象实验组,将数据经过一定的通道选择后,利用静息态参考的原理和Frobenius 范数将数据映射至特征空间,最后利用串联融合和样本层融合这两种方式求解融合矩阵。
此外,本文探讨了运动想象脑意图所对应的EEG 信号的特征是否具有可分解性与可组合性,即能否被拆解为若干个运动想象子过程与其对应的子特征。这个问题的产生主要源于在线的运行想象系统精细控制的需要。实验结果表明,运动想象确实可以通过某个统一的数学关系拆解为若干个子过程,而且该过程可逆。
值得说明的是,各个脑电设备、被试者和实验环境下通道选择的结果理论上来说具有一定差异。本研究的通道选择结果仅服务于运动想象过程与子过程的充分表达这一目的,因此该结果对所有的问题是否具有普适性需要进一步研究。
本研究尚存在值得进一步研究的问题,如能否研究出对不同被试者高泛化性的融合矩阵或融合算法。此外,实验过程中有数据证明,基于静息态参考和Frobenius 范数的特征向量表达对少样本、少通道高采样率的运动想象分类具有优秀的性质。一言以蔽之,本研究落实于EEG-MI 系统的精细控制,但道阻且长。在接下来的工作中,会将本文证明的MI 与其子过程相关脑电特征的分解与融合关系用于MI-BCI 系统中,并提高其性能。

