对称空间滤波器组自匹配的波束形成算法*
杨 烨,秦 云
(江苏大学,江苏 镇江 212013)
0 引言
阵列信号处理就是通过对传感器进行特定的排列来采集空间中不同的信号,并对采集到的信号进行处理的技术。在此基础上,对采集接收到的信号和空间中存在的干扰进行特定的处理,来获得对期望信号的最优接收的技术就是自适应波束形成技术[1]。自适应波束形成技术广泛应用于雷达、通信、电子对抗、射电天文[2-4]等领域,是阵列信号处理技术发展所带来的产物。自适应波束形成技术可以定向地接收空间中特定方向的信号,并且对其他方向上的干扰信号进行抑制,避免干扰信号对系统造成影响[5]。该技术实现这一功能的核心就在于对阵列天线的权值进行合理的设置,并根据环境的变化自适应地改变各阵元对应的权值,这样一来,阵列输出选择一个合适的权值进行补偿传播延时,以此获得期望方向上阵列输出的同向叠加,并且抑制其他方向上的干扰来波,实现对各来波方向信号的增强或者抑制,获得最优的阵列输出[6]。自适应波束形成算法就是通过获取各个阵元权值,实现在某种最优准则下的权集寻优[7]的算法。各个换能器阵列加权的权值系数组成的向量就是最优权矢量,通过最优权矢量的处理可以获得阵列方向图[8]。阵列方向图存在一个主瓣和多个旁瓣,方向图的主瓣决定了阵列的分辨率[9-10]。阵列分辨率的高低决定了阵列对空间信号的区分能力的高低,所以阵列方向图主瓣越窄,算法的性能越好。
为了获得更佳的性能,许多基于传统波束形成算法的延伸算法被提出,如文献[11]提出的一种变步长的约束稳定性最小均方(Constraint Stability LMS,CS-LMS)算法,在噪声环境下能够降低误差,提高算法的稳定性,有效滤除噪声对系统的影响;文献[12]将加载因子的选择与信号协方差矩阵的特征值挂钩,由特征值的特点来决定对角加载因子,加强了算法对干扰的抑制能力,而且在角度失衡的情况下也有较好的算法性能,但是加载因子的选择存在误差,使得系统的性能大幅度降低;文献[13]提出了根据不同导向矢量误差获取对应的加载量,但是最优加载值的求解方法运算量大且收敛速度也慢。以上这些方法虽然获得了更好的性能,但也带来了其他问题。此外,文献[14]提出的方法有效地提高了信噪比,在10 阵元情况下,其方向图主瓣宽度约为0.13,旁瓣约为-8 dB;在文献[15]提出的方法中,在10 阵元情况下,其方向图主瓣宽度约为0.18,旁瓣宽度约为-25 dB。这两种方法都是尽可能地提高信噪比,但是没有突破主瓣瑞利极限。
针对无法突破主瓣瑞利极限获得更窄主瓣和更低旁瓣这一问题,本文提出一种基于对称空间滤波器组自匹配的方法。该方法对相控阵阵元进行偏转调制,获得多组输出信号。对于主响应轴方向的波束分量,偏转调制响应是一个左右对称的向量,而其他波束分量的调制响应则不具备对称特性,因此将调制响应向量反转后进行匹配滤波,即可获得主响应轴波束分量的强度[16]。通过该种方法可以有效地滤除干扰信号的影响,增强期望信号的增益,并获得突破主瓣瑞利极限的阵列方向图。此外,结合传统的线性约束最小方差(Linearly Constrained Minimum Variance,LCMV)算法,对阵列的干扰方向进行零陷约束,从而进一步提高信噪比,获得更优秀的性能。
1 阵列信号模型
设定空间中存在N个信号源,信号从不同方向入射到M(M>N)元阵列上,则t时刻第(ii=1,2,…,M)个阵元接收到的信号为:
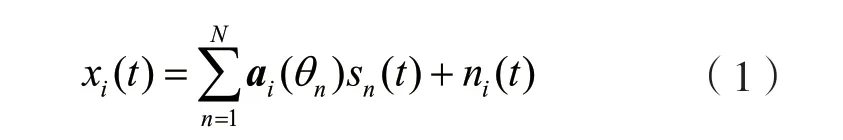
式中:sn(t)为第n个源信号;θn为第n个信号源的入射方向;ni(t)为t时刻第i个阵元接收到的高斯白噪声;ai(θn)为信号的导向矢量,表达式为ai(θn)=e-j2πf0τin,其中τin是第n个信号源到达第i个阵元相对于参考阵元的时延,f0为期望信号的频率。
均匀线阵所接收到的阵元数据用矩阵表示为:
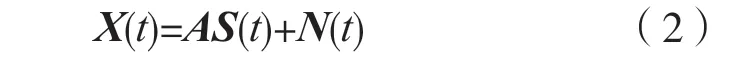
式中:阵列接收为X(t)=(x1(t),x2(t),…,xM(t))T;噪声为N(t)=(n1(t),n2(t),…,nM(t))T;信号源复包络为S(t)=(s0(t),s1(t),…,sN(t))T;矩阵A=(a(θ0),a(θ1),…,a(θN))是由n个导向矢量组成的,其中,a(θn)=(1,ejβl,…,ej(M-1)βl)T,βl表示第l个入射信号源入射到第二个阵元时相对于参考阵元的延迟。
2 对称偏转调制
本文在阵列调向的基础上进行延伸,提出了对称偏转调制,即通过对换能器阵列左右进行等角度、等次数的对称偏转调制获得多组阵列响应。对于主响应轴方向的波束分量,偏转调制响应是一个左右对称的向量,而其他波束分量的调制响应则不具备对称特性[16]。
2.1 换能器阵列输出信号
由n个换能器阵元构成阵列,在t时刻换能器阵列的输出为:

2.2 FIR 算法
利用基本的限长单位冲激响应(Finite Impulse Response,FIR)算法对n个阵元的阵列输出信号进行处理,即对各阵元输出进行加权和计算,计算公式为:

式中:yu(t)为n个阵元加权和的系统响应输出。
以矩阵形式表示为:

式中:γ(k)=RcT×w×v为系统对波数k分量的系统增益;为调向矢量;kc为主响应轴波数;为权矩阵;为阵列流形矢量。
2.3 对称偏转调制
对称偏转调制方法是阵列调向[17]这一基础方法的延伸,通过多次对称调向来获得偏转调制矩阵。
在主响应轴波数两侧一定范围内,等间隔对称设置m个偏转角度,分别得到相应的m个偏转矢量:
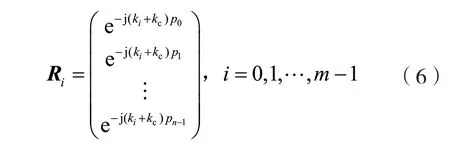
式中:ki为第i个偏转方向的波数。
则由m个偏转角度得到的偏转调制矩阵为:
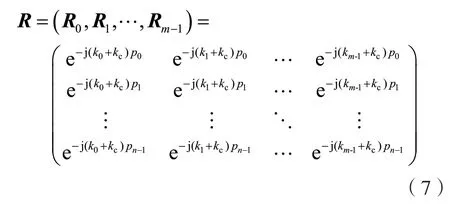
可得系统调制增益为:
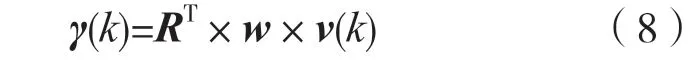
系统调制响应输出即为一个m维向量:
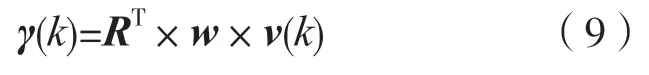
3 自对称匹配滤波
根据FIR 滤波器基本特性可知,对于主响应轴方向的波束分量,偏转调制响应是一个左右对称的向量,而其他波束分量的调制响应则不具备对称特性,因此将调制响应向量反转后进行匹配滤波[18],即可获得主响应轴波束分量的强度,其表达式为:

式中:JM为M维的方阵,表达式为其反对角线上的元素为1,其他元素为0。偏转调制后的自对称匹配滤波环节使得各个偏转角度的输出先进行对称,然后与对称之前的输出逐个相乘,最后累加获得系统的输出。
由于不具备左右对称的特性,因此非主响应轴方向的波束分量将被大幅抑制,而主响应轴波束分量则可以得到较高的增益。
4 仿真结果与分析
4.1 仿真实验
4.1.1 仿真1
阵列采用8 个阵元的标准线阵,阵元间距d设置为信号波长λ的一半,即d=λ/2。采样快拍数设置为K=1 200。基本FIR 算法的8 阵元阵列响应仿真如图1。
通过分析仿真图1,可发现当为基本FIR 算法的8 阵元阵列响应时,阵列方向图的主瓣半宽的正弦为0.12。

图1 基础FIR 算法阵列方向图
4.1.2 仿真2
阵列采用8 个阵元的标准线阵,阵元间距d设置为信号波长λ的一半,即d=λ/2。采样快拍数设置为K=1 200。对对称空间滤波器组自匹配波束形成算法进行仿真实验,对称偏转的角度设定为±3°,偏转次数设置为11 次,结果如图2 所示。
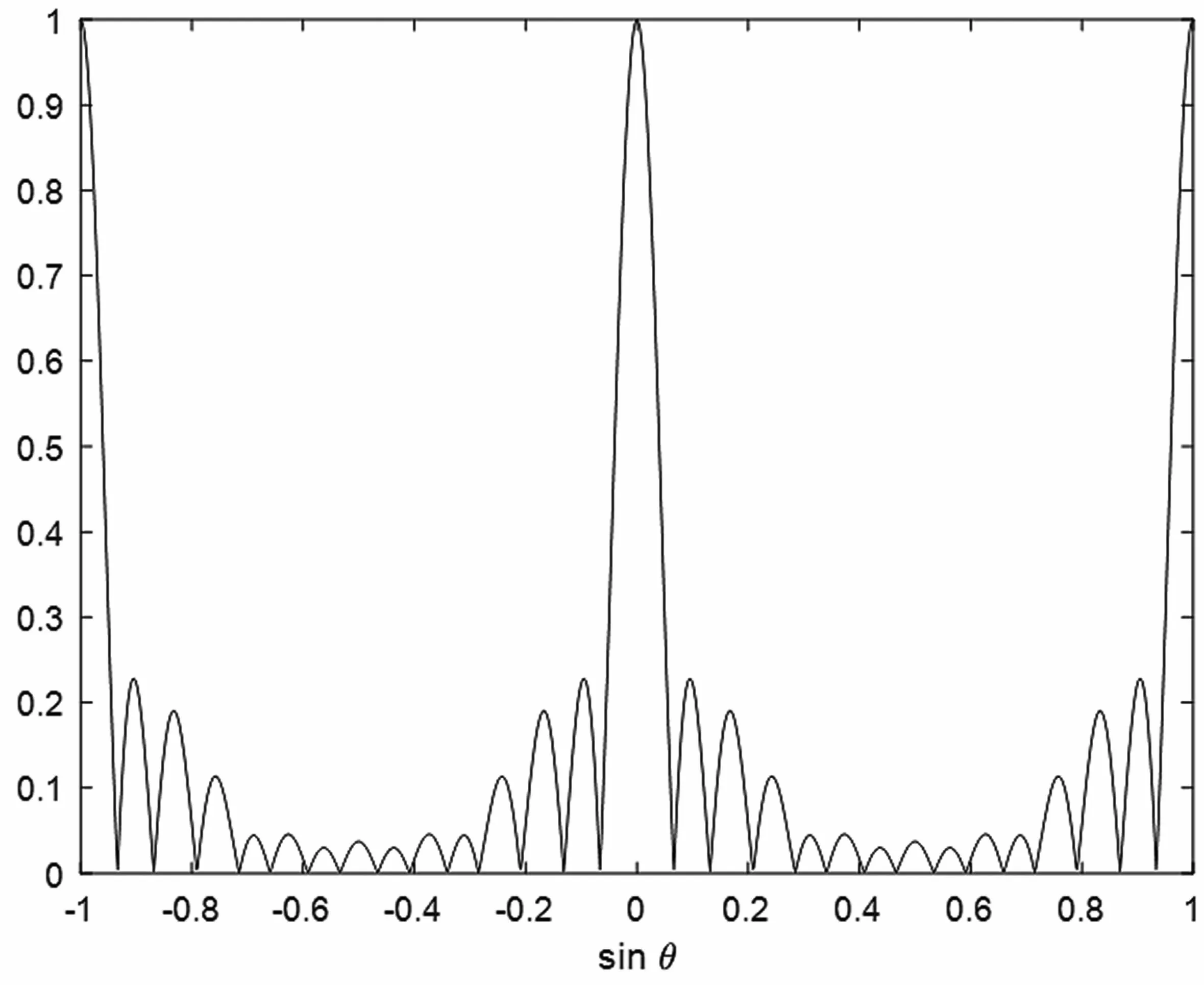
图2 空间自匹配滤波波束形成算法阵列方向图
通过仿真图2 发现,相较于基础的FIR 算法,通过对称空间滤波器组自匹配波束形成算法得到的阵列方向图主瓣更窄,对不同波束分量的滤波效果改善明显。本方法得到的方向图主瓣角度半宽的正弦仅仅是0.067,主瓣宽度降低到约为基本的FIR算法的一半。通过本文提出的算法,突破了主瓣瑞利极限,有效地收窄了主瓣宽度。
当两个及两个以上的不同频率信号输入非线性电路中时,会产生干扰,这种干扰称为互调干扰[19-20]。在本方法的实际运行中存在信号互调的现象。
假设仅有两个信源存在时,则:

式中:WH为权矢量矩阵。
X(t)的表达式为:
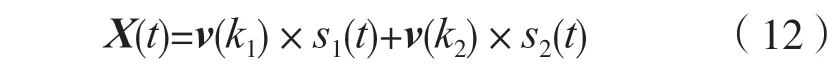
令Z1(t)=v(k1)×s1(t),Z2(t)=v(k2)×s2(t),则可推出:

可以看出,干扰信号在经过自对称匹配滤波器后会对期望信号产生干扰,两个波束分量之间存在互调。
两个信号之间互调的影响为:
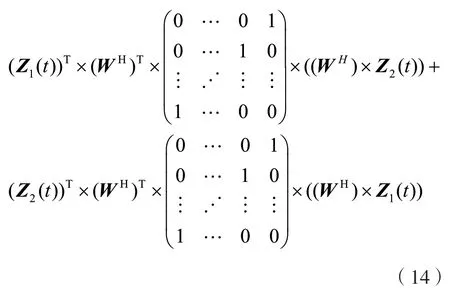
通过对上述公式的分析可以看出,两个信号的互调影响程度可以通过分析任一项干扰增益来获得。
4.1.3 仿真3
本文以第1 项互调干扰为例,通过两个流形矢量在不同入射角度时干扰增益的大小来判定其误差情况。当两个信号以各自的入射角度被阵元接收到信号时,会得到其对应的信号互调影响的大小。
设置16 阵元的阵列,阵元间间隔为d=λ/2 的均匀线阵,接收信号源为远场窄带信号。阵元的采样快拍数为1 200,波速为3 000 m/s。在-3°到3°之间平均选取了11 个偏转角度构造权矢量矩阵,将入射信号从-90°到90°,以1°为标准选取181 个入射点,可得到仿真图,如图3。
上述三维仿真图表示在两个入射信号情况下,其入射角度在-90°到90°之间变化时信号互调所产生误差的大小。由图3 分析可知,大多数情况下两个信号互调产生的影响基本可以忽略不计。当两个信号中有一个信号为0°入射时,另一个信号的入射角度会与之有一定的信号互调影响。

图3 两信号源不同角度入射下信号互调增益
由此可知,期望信号的入射角度为0°的情况下,两个干扰信号之间的互调影响基本可以忽略,只有期望信号与干扰信号之间会有一定的互调影响,但是也比较小。
4.1.4 仿真4
如图4 所示为进一步对仿真结果进行分析,分别对两个入射分量进行限定选取,分为以下三种情况:曲面正对角线方向,即两个分量具有相同的滤波,也就是某一个分量与其自身的滤波输出;曲面反对角线方向,即两个分量具有对称的滤波;水平中央方向,即主轴分量与其他分量的滤波。
通过分析可以发现,只有在期望信号与干扰信号互调时,才会出现较大的互调干扰。干扰信号在入射角度远大于偏转角度的情况下,它们之间的互调影响可以从三维图上清晰地看出基本为0。从图4(c)可以看出,只有在干扰信号的入射角度在偏转角度之内或者接近偏转调制角度时,期望信号与干扰信号之间才有比较大的干扰增益;当远离偏转调制的角度时,干扰信号与期望信号之间的互调影响很小。
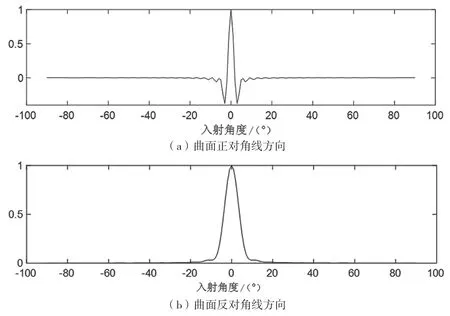

图4 两波束分量特定情况下互调分析
当曲面正对角线即两个分量具有相同滤波时,-10°到10°之间具有较大的增益,正对主轴方向的期望信号具有最大的增益。其他方向的干扰信号,当入射角度远大于选取的偏转调制矩阵的偏转角度时,其互调影响很小,相对于主轴方向的大增益来说基本可以忽略不计。也就是说,当干扰信号远大于偏转调制角度时,信号自身的增益对于仿真结果的影响可以忽略不计。结合三维仿真图的结果可以发现,只有在期望信号与干扰信号互调时才有较大的增益影响,干扰信号在入射角度远大于偏转角度的情况下,它们之间的互调影响近似为0。
4.2 分析与结论
通过以上几个方面的分析,可以看出本文方法在干扰信号来波方向的入射角比较大的情况下,能够得到较好的实现,并且通过选取远小于最小入射角的偏转角度构造偏转调制矩阵,可以最大限度地减小信号互调影响对本方法带来的影响。
当然,降低本文方法所带来的信号互调影响也是很有必要的。从式(13)中可以看出,信号的互调是必然存在的。为进一步优化算法性能,可以通过引入经典的自适应波束形成算法对权矢量矩阵进行约束处理。
5 引入LCMV 算法优化
经典的LCMV 算法可以通过设置权值矢量,使得波束方向图在特定来波方向上生成零陷[21]。在本文所提方法中,同样可以通过设置权值矢量,并带入权矢量矩阵中,获得一个可以在特定方向上得到零陷的权矢量矩阵,从而在已知的干扰信号来波方向生成零陷,抑制干扰对期望信号的影响。
设置16 阵元的阵列,阵元间间隔为d=λ/2 的均匀线阵,接收信号源为远场窄带信号,进行仿真实验5。阵元的采样快拍数为1 200,波速为3 000 m/s。在-3°到3°之间平均选取了11 个偏转角度构造权矢量矩阵,将入射信号从-90°到90°以1°为标准选取181 个入射点,假定干扰信号以-20°、30°为入射角度。引入LCMV 算法后对本文算法可得到仿真结果如图5 所示。

图5 引入LCMV 算法零陷约束
从三维仿真图5 可发现,仿真图在-20°和30°的干扰方向上形成了较深的零陷,期望信号与干扰信号在以-20°和30°为入射角度入射时,产生的信号互调影响受到了极大的抑制,说明所提方法能够有效地去除在空间自匹配滤波过程中由于信号互调所产生的干扰。
设置16 阵元,阵元间间隔为d=λ/2 的均匀线阵,阵元的采样快拍数为1 200。空间中有3 个完全不相干的信源,来波方向角度为[0,-40°,20°],对应的信源波束为[0,-0.64,0.34]。对经典的LCMV 算法和LCMV 优化的本文算法进行仿真对比,结果如图6所示。

图6 LCMV 算法和LCMV 优化的本文算法
通过图6 可知,LCMV 算法优化后得到的偏转调制线性约束最小方差(Deflect Modulation Linearly Constrained Minimum Variance,DM-LCMV)波束形成算法,可以在干扰信号的来波方向(即仿真图中光标位置)形成零陷,进一步降低干扰信号对系统的影响。同时,阵列方向图的主瓣半宽由LCMV 算法的0.13 收窄至0.11,阵列方向图的主瓣宽度突破瑞利极限,算法的性能得到了提升。
6 结语
本文提出了一种基于对称空间滤波器组自匹配的波束形成算法,能够有效地得到主瓣更窄的阵列方向图,突破主轴的瑞利极限。该方法通过对换能器阵列得到的输入信号进行对称偏转调制,获得系统调制响应的输出,然后对其进行自对称匹配滤波。由于对于主响应轴方向的波束分量,偏转调制响应是一个左右对称的向量,而其他波束分量的调制响应则不具备对称特性,因此将调制响应向量反转后进行匹配滤波,可获得主响应轴波束分量的强度,在此情况下,阵列的方向图突破了主瓣瑞利极限的限制。而由于信号互调的存在,本文又引入了LCMV 算法对干扰信号进一步抑制,在干扰方向上形成零陷,提高了算法的性能。

