短波宽带数字下变频设计与仿真*
田 波,程云鹏,罗庆驰
(中国人民解放军陆军工程大学,江苏 南京 210007)
0 引言
短波通信依靠1.5~30 MHz 的电磁波进行信号传输,是最早出现并被广泛应用的无线通信方式,至今仍是中远距离无线通信的重要手段。短波信道传播特性异常复杂,其理论和技术仍处于不断完善和发展的过程中[1]。传统短波通信系统的带宽为3 kHz[2],由于在此带宽下分配短波通信频段的惯例沿用至今,短波通信系统通常支持不超过2 400 bit/s速率下的数据传输。
在2011 年和2017 年,美军波形标准MILSTD-188-110C[3]和MIL-STD-188-110D[4]相继颁布。110C 采用了宽带数据传输技术,将短波通信带宽由3 kHz 扩展到3 kHz 倍数,最高可支持24 kHz[5],110D 进一步将信道带宽扩展到48 kHz,这些波形大大提高了数据传输的效能[6-7]。在波形体制方面,有代表性的是多载波并行、单载波串行和宽带单载波频域均衡技术[8],传输速率均可达到4 800 bit/s 以上,支持高清图像、实时视频等宽带高速数字业务。
实现短波宽带高速业务需要宽带信道的支撑。随着模数/数模(AD/DA)器件的发展,高性能的模数/数模转换得以实现,由此软件无线电技术开始兴起。同时,短波信道技术引进了软件无线电的思想,开始采用数字化的实现方式,并从过去的模拟信道向数字化信道逐渐过渡。短波信道数字化的核心是数字下变频技术。数字下变频的运算速度和运算精度决定了其输入的最高采样速率和接收性能指标,所以数字下变频必须进行优化设计[9]。短波宽带数字下变频主要有中频数字化和射频数字化两种方式,在此基础上相继开展了一些单信道、多信道、等间隔并行信道的研究工作。在文献[10]中,作者介绍了一种短波中频数字化的实现方式,中频信号下变频到3 kHz 带宽信号。在文献[11]中,作者采用了射频数字化的实现方式,将射频信号下变频至12 kHz 带宽的信号。
根据以上短波数字通信技术的研究现状,结合工程实际,本文针对短波宽带高速数字业务传输需求,设计了一种基于射频直接采样的短波24 kHz 数字下变频结构。本结构的核心在于多级滤波器的总体设计,通过分析数字下变频的指标和各类滤波器的特性,采用级联积分梳状(Cascaded Integrator-Comb,CIC)滤波器、CIC 补偿滤波器和有限长脉冲响应(Infinite Impulse Response,FIR)滤波器的三级级联数字下变频结构,并引入多相结构加以仿真实现。
1 数字下变频基本实现结构
图1 给出了数字下变频基本实现结构,这是一个多级实现结构,其信号处理的流程为:首先射频模拟信号通过高速AD 采样转换成数字信号,与数字控制振荡器(numerically controlled oscillator,NCO)产生的正交本振信号进行混频;其次通过由CIC 滤波器、CIC 补偿滤波器、FIR 滤波器组成的多级实现结构进行滤波抽取等处理,实现高采样速率到低采样速率的变换,便于后续进行基带处理。

图1 数字下变频实现
由以上处理流程可以看出,数字下变频实现结构中的CIC 滤波器、CIC 补偿滤波器、FIR 滤波器是数字下变频设计需要重点关注的模块。
CIC 滤波器是一种高效的数字滤波器,其本质上是一个矩形序列,滤波过程无乘法运算,可大幅减少运算复杂度。由于CIC 滤波器的阻带衰减不够,在实际工程中通常采用多级级联的实现形式。CIC滤波器的幅频特性具备Sa 函数特点,用于抽取时通带存在频谱混叠,所以CIC 滤波器设计首先需要考虑抗混叠问题[7],图2 给出了CIC 滤波器的抗混叠特性。
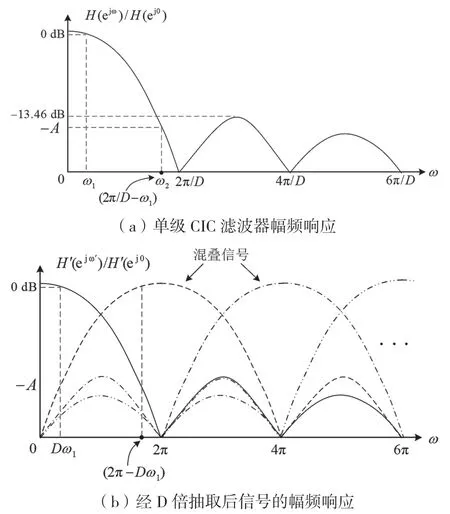
图2 CIC 滤波器抗混叠特性
从图2 可以看出,频率为2kπ-Dω1~2kπ+Dω1(k为整数,且k≠0)的混叠信号将会叠加到通带频率成分为-Dω1~Dω1的有用信号上。由于CIC滤波器特有的Sa 函数幅度特性,所有混叠信号在频率ω2=2π-Dω1处的衰减程度是最小的。如果CIC滤波器阻带在ω2处的幅度衰减足够大,那么所有混叠信号对有用信号的影响可忽略不计。因此,ω2=2π-Dω1的衰减值可以作为CIC 滤波器抗混叠能力的指标。CIC 滤波器的阻带抗混叠衰减A为:

由于CIC滤波器通带幅度不平坦,随着ω1增加,幅度逐步下降。所以衡量带内平坦度的指标常采用通带幅度容差δp的计算公式:

CIC 补偿滤波器的主要功能是补偿CIC 滤波器通带幅度不平坦和频响的下降,经CIC 补偿滤波器补偿后,通带幅度容差可保持在设计指标范围内。
FIR 滤波器是一种有限长单位冲激响应的滤波器,其作用是保证整体滤波器的通带、阻带要求,并进行抽取滤波处理。由于FIR 滤波器在采样率较高时计算复杂度过高,一般将其配置在数字下变频结构的最后一级。
2 基于多级实现的数字下变频设计
对于短波宽带信道,考虑采用射频数字直接采样技术,通过数字下变频,实现从射频数字信号到基带信号的抽取转换,主要设计参数如表1 所示。

表1 数字下变频器设计指标
由数字下变频器的设计指标,计算可得总的抽取倍数为1 200,需要合理分配三级滤波的抽取倍数。为减少整体计算复杂度,比较合理的设计方案是第一级低复杂度CIC 滤波器的抽取倍数尽可能高一些[12],为后续CIC 补偿滤波器和FIR 滤波器的低抽取倍数处理提供便利。
2.1 CIC 滤波器设计
CIC 滤波器为矩形序列,其阶数就是抽取倍数。依据上节对CIC 滤波器的抗混叠衰减值等指标的分析,可计算出不同抽取倍数和级联级数下,通带幅度容差和阻带抗混叠指标如表2 所示。

表2 不同抽取倍数下的CIC 指标对比
由表2 可以看出,CIC 滤波器抽取倍数D越大,通带幅度容差δp越大;级联级数Q越大,阻带抗混叠衰减程度越大,但也导致通带幅度容差加大。考虑到CIC 滤波器复杂度较低,采用比较大的抽取倍数时,可显著地降低后续CIC 补偿滤波器和FIR滤波器的阶数,降低整体设计的计算复杂度。综合权衡后这里抽取倍数选取300 倍,采用3 级级联,抗混叠指标为64.23 dB,满足60 dB 的设计要求。
利用MATLAB 软件设计CIC 滤波器的关键语句如下:
fpass=24300;fs=92 160000;Dcic=300;Acic=60;
hcic=design(fdesign.decimator(Dcic,‘cic’,1,fpas s,Acic,fs));
hd=cascade(dfilt.scalar(1/gain(hcic)),hcic);
fvtool(hd,‘Fs’,fs);
通过仿真画出CIC滤波器幅频响应,如图3所示。可以看出,抽取300 倍后的采样频率为307.2 kHz,ω1处通带内幅度容差约为0.269 dB,此时阻带抗混叠衰减的实际指标约为64.23 dB,仿真结果与指标分析一致。
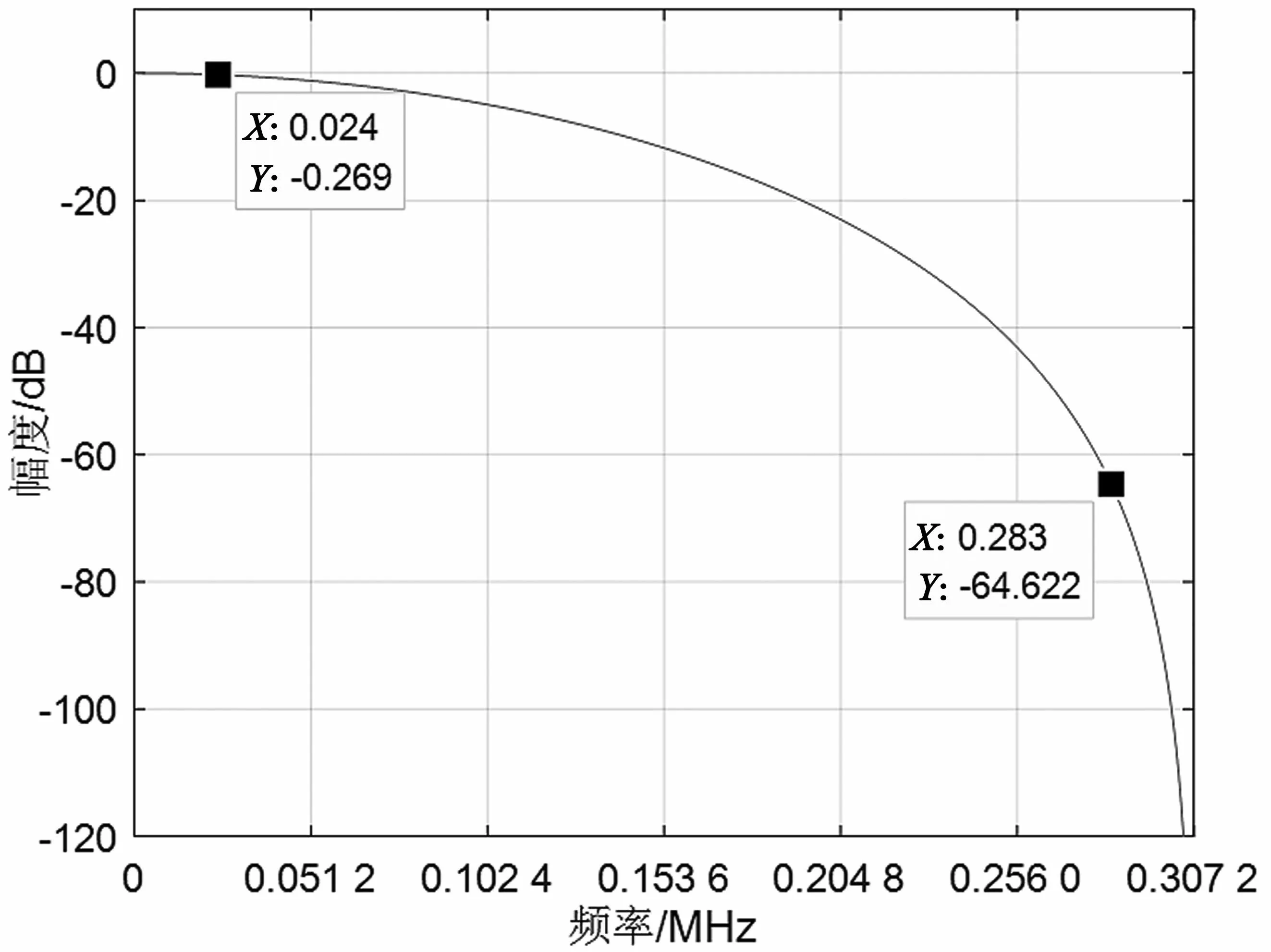
图3 CIC 滤波器幅频响应
2.2 CIC 补偿滤波器设计
经CIC 滤波器300 倍抽取后,其剩余抽取倍数为1 200/300=4 倍,可设计CIC 补偿滤波器和FIR滤波器的抽取倍数各为2 倍。由于多级级联时通带波动随级数增大而增大,考虑将小于0.02 dB 的通带波动指标分配至CIC 补偿滤波器和FIR 滤波器设计中,各小于0.01 dB。
通过MATLAB 软件,对CIC 补偿滤波器进行仿真设计,并给出关键语句如下:
Dciccomp=2;fpass=24300;fstop2=76800;
delta_comp=0.01;Acomp=60;fs2= 307200;
hciccom=design(fdesign.decimator(Dciccomp,‘ciccomp’,hcic.differentialdelay,hcic.numberofsections,fpass,fstop2,delta_comp,Acomp,fs2));
fvtool(hciccom,‘Fs’,fs2);
图4 和图5 分别给出了CIC 补偿滤波器幅频响应和系数,由图4 可见CIC 补偿滤波器的通带较为平坦,通带范围和阻带衰减均满足设计指标要求。由图5 可以看出滤波器系数为21 个,较为合理。
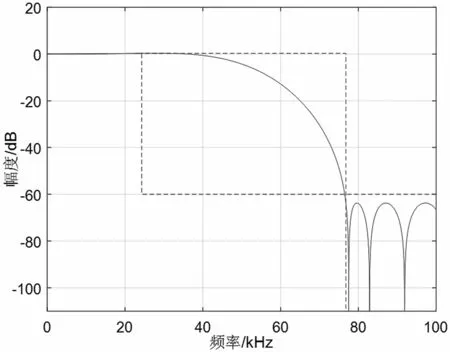
图4 CIC 补偿滤波器幅频响应
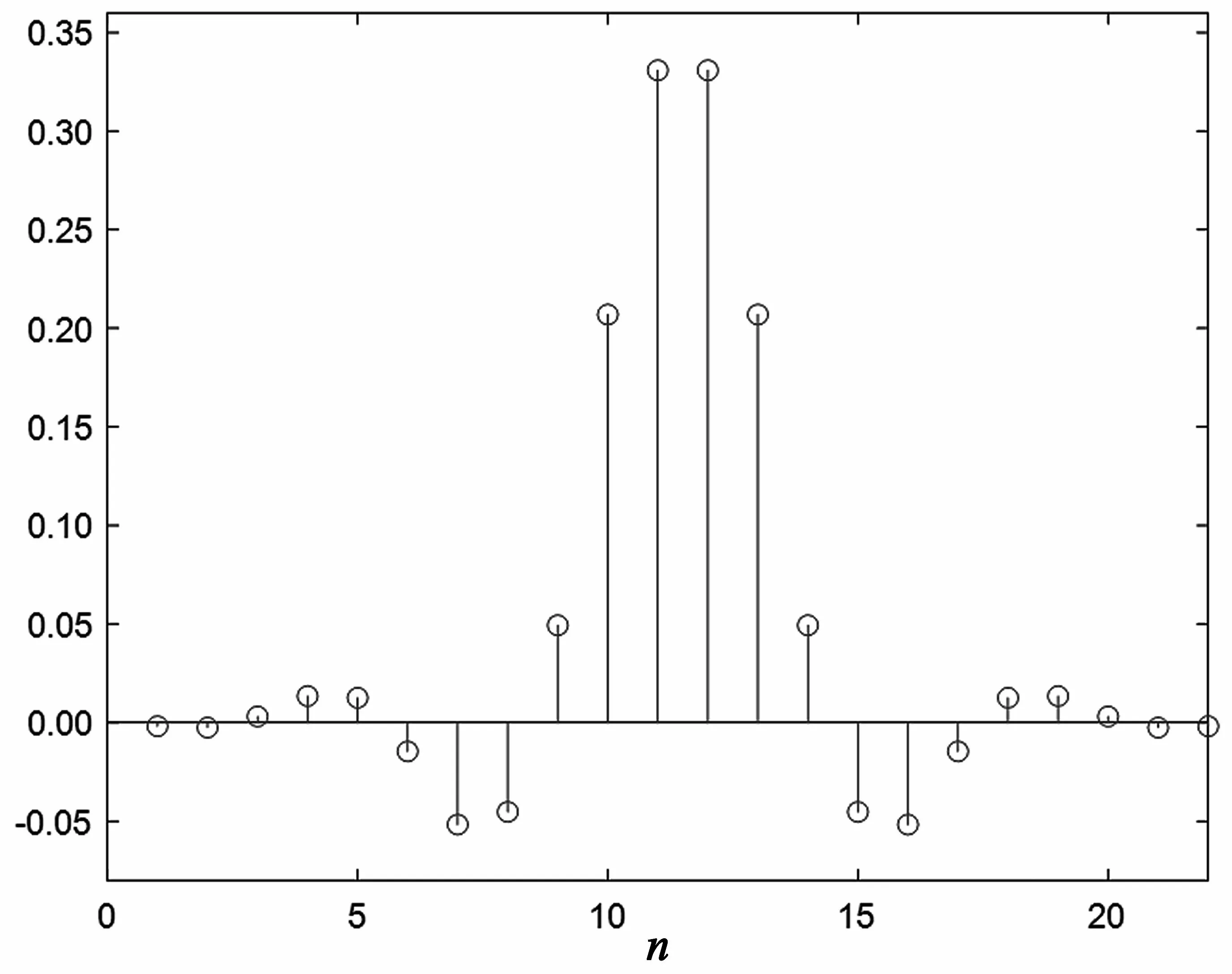
图5 CIC 补偿滤波器系数
为更好地对比补偿效果,利用MATLAB 软件合成CIC 滤波器和CIC 补偿滤波器,关键语句如下:
h=fvtool(hd,hciccom,cascade(hd,hciccom),‘Fs’,[fs fs2 fs],‘ShowReference’,‘off’);
图6 和图7 分别给出了CIC 补偿效果对比和放大效果。由图6 可以看出,通带被限制在截止频率为24.3 kHz 范围内,阻带衰减满足-60 dB 要求,但过渡带较宽,需要后续FIR 滤波器加以限制。由图7 可见,通带内CIC 滤波器的幅频响应逐渐下降,补偿滤波器逐渐上升,补偿后通带平坦度很好,达到了设计指标要求。

图6 CIC 补偿效果

图7 CIC 补偿放大效果
2.3 FIR 滤波器设计
级联第三级使用FIR 滤波器,抽取倍数为2 倍,利用MATLAB 软件设计FIR 滤波器,并对三级级联滤波器进行合成。FIR 滤波器设计关键程序如下:
Dfir=2;fpass=24300;fstop3=28800;
delta_fir=0.01;Afir=60;fs3= 153600;
hfir=design(fdesign.decimator(Dfir,‘Lowpass’,fpass,fstop3,delta_fir,Afir,fs3));
fvtool(hfir,‘Fs’,fs3);
合成三级级联滤波器的关键程序如下:
fvtool(hd,hciccom,hfir,cascade(hd,hciccom,hfir),‘Fs’,[fs fs2 fs3 fs],‘ShowReference’,‘off’);
图8 和图9 分别给出了FIR 滤波器幅频响应和三级滤波器级联幅频特性放大图。可以看出,三级滤波器级联后,过渡带已变窄,阻带衰减约为60 dB。
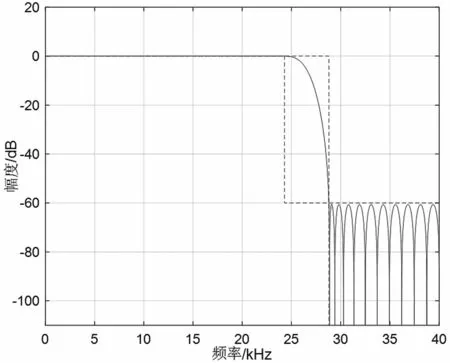
图8 FIR 滤波器幅频响应

图9 三级滤波器级联幅频特性
至此,完成基于CIC 滤波器、CIC 补偿滤波器、FIR 滤波器的三级级联数字下变频的设计结构。以I 路为例,其三级级联抽取结构如图10 所示。

图10 数字下变频三级级联抽取结构
3 基于多相结构的数字下变频设计
多相结构就是按相位均分的原则将数字滤波器的转移函数H(z)分解成若干个不同的相位组,形成多个分支,并在每个分支上设计数字滤波的结构,即采用多个低阶的分支滤波器来实现原有高阶滤波器的滤波功能[13]。多相结构的优势在于复杂度较低,易于工程实现,能高效地进行实时信号处理,被认为是软件无线电研究中最有用的工具[7],常被用于因高采样率数字滤波器阶数过高而不易实现的滤波结构中。
在上述数字下变频设计中,滤波器始终位于抽取之前,即在高采样率端进行,对运算速度有较高的要求。利用多相滤波结构可以将部分滤波功能转移到低采样率端进行。
3.1 CIC 多相结构实现
图11 给出CIC 滤波器的多相实现结构。(a)为普通数字滤波器的抽取实现,其中H(z)为滤波器转移函数,此时滤波在高采样率端进行;(b)为CIC滤波器的实现图,1/(1-z-1)Q为级联的积分器,1/(1-z-1)Q为级联的梳状滤波器,可看出滤波器仍在高采样率端;(c)为等效变换后的多相结构,梳状滤波是在抽取后的低采样率端进行的。
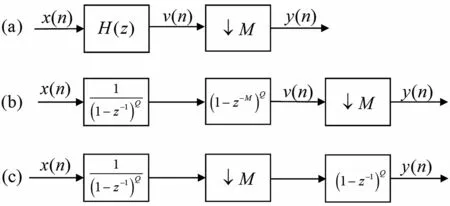
图11 CIC 多相实现结构(M=300,Q=3)
3.2 CIC 补偿/FIR 滤波器多相结构实现
CIC 补偿滤波器本质上还是FIR 滤波器,使用FIR 滤波器的多相结构实现。如果FIR 滤波器阶数与抽取倍数不是整数倍系数,可补零形成多相结构。考虑到抽取倍数都为2,两种滤波器的多相实现结构设计如图12 所示。
图12 中,(a)为FIR 滤波器的抽取实现;(b)中Ek(zM)为多相分量,共有M个,z-1为延迟单元,此时滤波在高采样率端进行;(c)中利用等效变换将Ek(zM)与↓M变换位置,构成多相结构。

图12 CIC 补偿/FIR 滤波器多相实现结构(M=2)
4 仿真与分析
本节对数字下变频整个处理过程进行了仿真,输入信号采用典型的单音和多音信号,通过分析各级滤波处理后的信号时频域特性,验证设计是否合理。仿真分别针对多级结构、多相结构进行,两种结构下各级信号完全一致,说明了多相结构的有效性。
4.1 单音信号
设载波频率为9.216 MHz,射频单音信号频率为9.216 600 MHz,相当于上边带信号的单音频率为600 Hz,那么NCO 对应输出频率为9.216 MHz,经NCO 混频后的上边带信号频率为600 Hz。在载波相位同步情况下,各级滤波器输入输出信号的时域波形如图13 所示。
由图13 可以看出,单音信号经过每一级滤波后的幅度和周期中,幅度均保持一致,周期变化与滤波器抽取倍数变化完全相符。

图13 单音信号的时域波形对比
4.2 多音信号
多音信号采用频率为600 Hz,1 200 Hz,2 400 Hz,3 200 Hz,4 800 Hz,6 400 Hz,7 680 Hz,9 600 Hz,12 800 Hz,19 200 Hz,25 600 Hz,28 800 Hz 的上边带信号,数字下变频后的基带采样频率为76 800 Hz。由于该采样频率正好是多音信号中600~ 25 600 Hz的整数倍,在快速傅里叶变换(Fast Fourier Transform,FFT)频谱分析时,可以避免频谱泄露,便于观察通带幅度值及平坦度,频率28 800 Hz 用于观察阻带衰减。
图14 给出了各级滤波器输入输出信号的时域波形,可以看出,多音时域信号经过每一级滤波器的幅度一致,波形点数与滤波器抽取倍数一致。

图14 多音信号的时域波形对比
图15 给出了多音信号的频域幅度特性对比,经CIC 滤波、CIC 补偿滤波抽取后,通带截止频率24.3 kHz 内各频率幅度都比较一致,最后FIR 滤波器输出信号通带频率幅度波动小于0.02 dB;过渡带内25.6 kHz 频率衰减1.5 dB,28.8 kHz 带外信号衰减达到60 dB 以上,达到了设计要求。

图15 多音信号的频域幅度特性对比
5 结语
本文设计了一种基于射频直采的短波宽带数字下变频结构,适用于短波24 kHz 带宽高速业务传输,设计关键在于CIC、CIC 补偿和FIR 滤波器。通过讨论各级滤波器的多相实现结构,并结合单音和多音信号进行了仿真与分析,验证了设计的可行性。结果表明,该设计整体通带波动和阻带衰减等指标均达到指标要求,可以应用于工程实现。
—— “T”级联

