创设梯度式训练 落实引导式评讲——以“轴对称图形”专题训练、评讲为例

⦿江苏省响水县实验初级中学 刘海云

1 引言

有些专家认为学习知识的动力就如海绵里的水，只要愿意挤，总还是有的.这句话不无道理，因此，很多数学教师课后或者是专题复习时都会布置“海量”的作业或训练题，以巩固所学的知识，用这种方法提高学生的学习成绩.其实，多年的教学实践表明，布置“海量”的作业或训练题对一部分学生的学习成绩适得其反.究其原因，在于这部分学生只是为了完成教师布置的“海量”作业而机械地重复训练，在做题过程中没有领悟数学思想、方法，只是模仿例题、套公式去解题.基于此，笔者以“轴对称图形”专题训练、评讲为例，谈谈创设梯度式训练去落实引导式评讲的一些做法，旨在把学生对数学知识的“内化”做精、做细.

2 设置适当的梯度式训练，促进学生的思维由浅入深发展

数学课堂教学的意义在于培养学生的思维能力.数学的思维训练是通过许多重要的教学环节环环相扣整合在一起进行的，其中让学生完成作业或专题练习是一个重要的教学环节.因为作业或专题练习可以促使学生巩固和消化在课堂教学中所获得的数学知识或技能，进一步理解数学思想方法，并能灵活应用知识对问题情境进行数学建模.因此，作业或专题练习是使学生掌握知识，形成技能，帮助他们构建运用知识解决实际问题的有效途径.那么，如何设置数学作业或专题练习？笔者在多年的教学实践中总结出了一套行之有效的方法，那就是设置的数学作业或专题练习应该具有梯度.例如，对“轴对称图形”专题训练，可以这样设置：

类型一：以选择题作为基础题，预设形式.

(1)图1是几家银行的标志图案，其中不属于轴对称图形的是( ).

A B C D图1

图2

(2)同学甲站在一面镜子前，从镜子中看到他背后墙上的电子钟显示的时间是图2所示的形式，此时的时间应该是( ).

A.10：51 B.10：21 C.15：01 D.12：01

类型二：以填空题作为中档题，预设形式.

(3)已知点M(a，3)和N(2，b)是关于x轴的对称点，则(a+b)2021=.

(4)将一张10 cm×6 cm的矩形纸片ABCD(如图3)进行折叠，使AD边落在AB边上，成为图4，再次将△ADE以DE为轴向右折叠，AE与BC交于点F，如图5，则所得的△CEF的面积是.

类型三：以推理、计算题作为拔高题，预设形式.

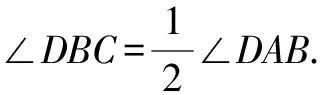
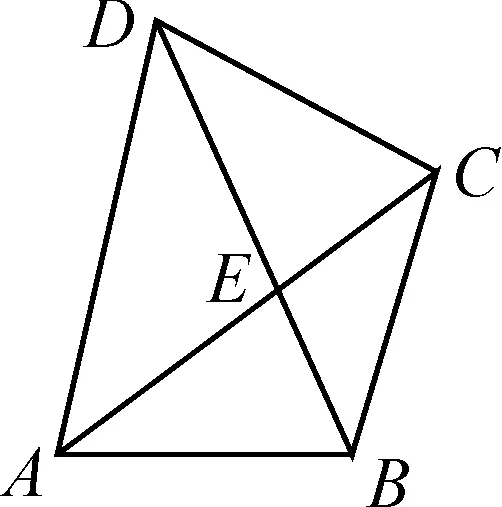
图6

图7

(6)如图7，△ABC中，已知∠CAB和∠ABC的平分线相交于点F，过点F作DE∥AB，分别交AC于点D，交BC于点E，若AD+BE=m，求线段DE的长.

设计意图：专题练习分为三类题型，让学生从命题形式上认知解决问题情境的多样性.另一方面，将同一类型分为不同的层面，而且各题之间形成一定的梯度，需要学生应用不同的知识点解决问题.这种设置可以让学生通过对问题情境的数学建模，夯实基础，巩固知识，拓展思维.

3 针对作业或专题练习引导系统复习，促进学生的思维由点到面发展

作业或专题练习有利于帮助学生理解、掌握和运用数学概念、定理、公式和法则.因为作业或专题练习是教师用作示范的具有一定代表性的典型数学质疑情境，是把数学知识、技能、思想和方法联系起来的桥梁，是对知识、技能、思想和方法进行分析、综合和运用的重要手段.因此，指导学生在完成作业后首先进行系统性的复习，可以回忆已学的知识内容，回放公式、定理等，将它们整合成相应的知识框架.比如，笔者对“轴对称图形”专题知识进行整合分为三个方面，首先是概念，其次是性质，最后是应用.在指导学生做题时，应用是很重要的，多年的教学实践表明，应用是不可缺失的环节，它是解决问题的关键所在.“轴对称图形”有下列特点：

(1)画轴对称图形的方法：首先确定对称轴，然后利用轴对称的性质，找出特殊的对称点(一般为图形的角的顶点)，依次连接找出的点构成图形.

(2)若一个三角形有两个角相等，这两个角所对的边也相等，图形关于两角所夹的边的中垂线对称.

(3)三个角相等或者三条边相等的三角形，是等边三角形.

其中特点(2)(3)是轴对称几何图形的应用，这里仅以三角形为例，四边形等大家自己探讨.

4 反思解题过程，促进学生的思维由简单到复杂发展

数学作业或专题练习与教学过程中教师提出的问题关联密切，其概念内涵上有一定的重合，但也有所不同.一般来说，作业或专题练习主要是为教学服务的，是针对知识与能力要求而设置的，通过让学生做作业或专题练习，起到加深巩固所学数学知识的作用.作业或专题练习是具有指向性和目标性的，而问题所涵盖的知识、涉及的因素范围较广，也可以超出数学学科知识.所以，不是课堂上教师提出的问题就能涵盖一切，只有对作业或专题练习及时评讲与反思，才能促进学生的思维由简单到复杂发展.

比如，对于前面给出的“轴对称图形”专题训练类型一的第(2)题，笔者采用多媒体制作如图8所示的图形，让学生分析镜像与物体之间是这两种形式中的哪一种对称方式，从而对镜像与物体之间的轴对称进行数学建模.

图8

又如，对于类型三的第(6)题，让学生明晰“∠CAB，∠ABC的平分线”有什么意义(平分角)，以及DE∥AB有什么意义(内错角相等，可以得出△DAF和△EBF是等腰三角形)，解决了这两个问题，该题的计算结果也就出来了.

通过对作业或专题练习的及时点评与解题过程的反思，做到了学法引路.通过点评分析，把陈述性知识变成了一种策略和可操作的流程，让学生明白接下来该怎么解决问题，达到事半功倍的效果.另一方面，又可以让学生重视归类、审题、书写等问题.

5 结束语

总之，作业或专题练习是面向全体学生的一种常规训练，在训练难度、技巧上应该是服务多数学生的.笔者相信，只要设置的作业或专题练习具有适当的梯度，就能促进学生的思维由浅入深发展；只要针对作业或专题练习引导系统复习，就能促进学生的思维由点到面发展；只要及时反思作业或专题练习解题过程，就能促进学生的思维由简单到复杂发展.