不同含水率砂岩蠕变试验及损伤模型研究

蒋 成，张树光，刘新民，张 研，刘文博

（1.桂林理工大学土木与建筑工程学院，广西桂林 541004；2.桂林理工大学广西岩土力学与工程重点实验室，广西桂林 541004；3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉 430071；4.中国科学院大学，北京 100049）

0 引 言

围岩蠕变特性主要指在恒定外荷载作用下应变随着时间推移持续增大［1-4］；一般可以描述为隧洞围岩在施工扰动和高地应力等外部条件作用下，在经历短暂的压缩变形之后，便进入了漫长蠕变变形阶段，此时隧洞围岩的力学性质会随着时间的推移逐渐产生劣化［5-7］，具体表现为围岩内部裂缝、空隙不断发育、扩展，直至蠕变变形进入到加速蠕变变形时，裂缝、空隙才会逐渐贯通形成明显的断裂面，使得引水隧洞围岩失稳变形破坏［8］。同时，引水隧洞围岩会长期受到隧道中水流冲刷的影响，水的浸入会导致岩体颗粒间胶结作用下降，促进岩石内部裂隙的快速发展，使岩石更易发生变形破坏。

王萍等［9］采用水浸泡后的岩石开展了水岩耦合蠕变试验，并采用核磁共振技术探究发现岩石内部裂隙在水化作用下会快速扩展、贯通导致岩石损伤扩大，后依据核磁共振结果构建了水岩耦合蠕变模型。黄明等［10］发现随含水率增大泥质粉砂岩的蠕变模量越小，并结合该变化规律建立了蠕变模型。杨彩红等［11］开展了含水率对岩石蠕变变形影响的试验，并分析得出岩石的蠕变变形与速率会随含水率的增大而增大。张春梅等［12］通过对不同含水条件下的砂岩进行蠕变力学特性试验，分析得出随浸水时间的增加，试样瞬时应变与蠕变应变逐渐增大，且其长期稳定强度发生剧烈衰减。孙彦峰等［13］通过对不同含水率砂岩的蠕变试验，发现随含水率的增大试样的瞬时应变与破坏应变逐渐增大，长期强度则逐渐降低。

综上所述，含水率对岩石的蠕变性能具有较大的影响，且强度特性均会随着含水率的增大而产生的劣化现象。因此，对全州某引水隧洞围岩开展不同含水率状态下的单轴加载蠕变试验，分析不同含率对岩样蠕变变形特性的影响，并构建一种考虑含水率和时间双重影响的新型非定常蠕变模型，为引水隧洞工程中的蠕变变形问题提供一定的理论依据。

1 蠕变模型的建立

1.1 一维非定常分数阶模型构建

西原体蠕变模型是由胡克体、开尔文体以及理想黏-塑性体串联所组成，被广泛的运用于描述岩石的黏-弹-塑性蠕变变形特征，其力学模型见图1，方程表达式见式（1）［14］。

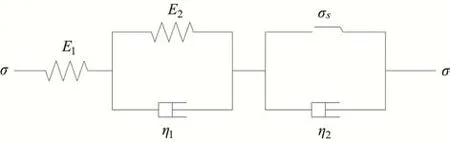
图1 西原模型Fig.1 Nishihara model

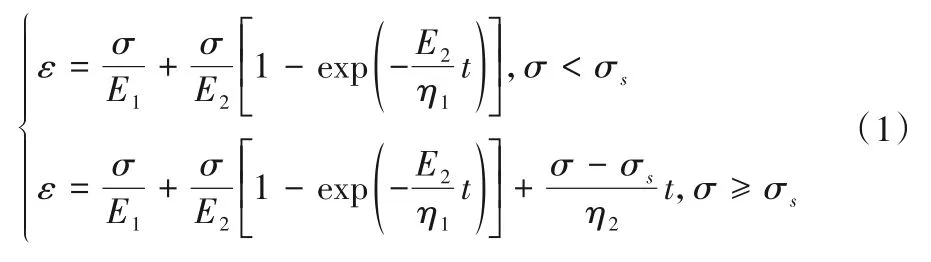
式中：E1为弹性模量；σ为施加的蠕变应力；E2为黏弹性模量；η1为黏滞性系数；t为蠕变时间；η2为黏塑性模型的黏滞性系数；σs为岩体屈服强度，MPa。

传统的西原体模型能较好的反映蠕变变形过程中的衰减蠕变阶段与稳定蠕变阶段，但其难以描述加速蠕变阶段的蠕变变形曲线。为准确的对不同含水率岩样的蠕变全过程进行描述，引入了分数阶黏壶替代西原体中的塑性黏壶，并结合考虑含水率和时间双重影响的损伤系数D，构建出一种新型的非定常分数阶蠕变模型。其中分数阶黏壶蠕变方程表达式为［15］：

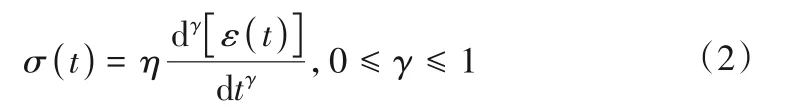
式中：γ为分数阶阶数；η为黏滞性系数。

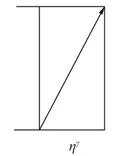
图2 Abel黏壶体Fig.2 Abel dashpot

在含水率和应力的双重影响下，岩石损伤系数D包括以下两部分：①由含水率引起的损伤Dw，②岩样在加载过程中随时间产生的损伤Dt。假设含水率为0%时，岩样不会产生损伤，则损伤变量Dw可表示为：

式中：Dw为关于含水岩石的损伤变量；E0为干燥岩石的初始弹性模量；Ew为含水岩石的弹性模量。

岩样在加载过程中随时间产生的损伤Dt则可可表示为：

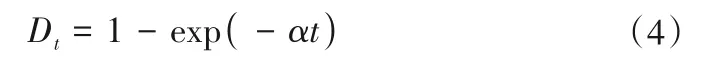
式中：α为非定常系数；Dt为关于时间的损伤变量。

故损伤变量D满足以下关系［15］：

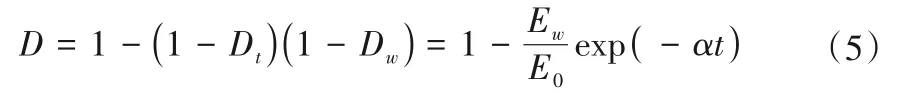
1.2 非定常黏塑性应变确定

整数阶黏壶转化为分数阶Abel黏壶，可得：

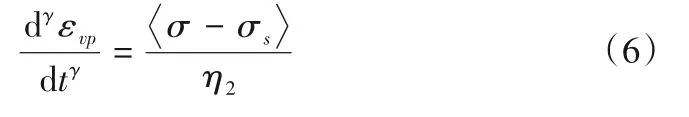
式中：η2为黏塑性体的黏滞性系数。

其中，＜σ-σs＞满足以下条件：

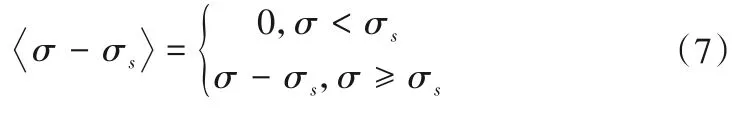
当σ≥σs时，对式（5）进行积分求解得到：

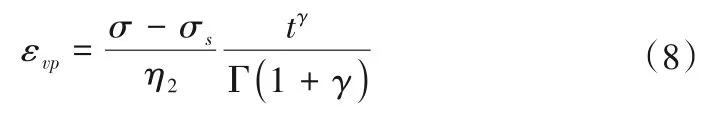
将黏滞性参数转换为含时间损伤变量和含水损伤变量的形式为：

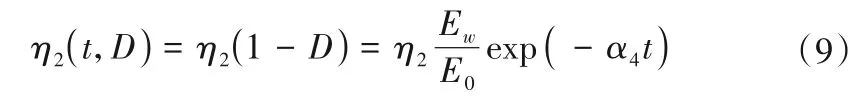
式中：α4为分数阶Abel黏壶的损伤系数。

将式（8）代入到式（7）中，得：

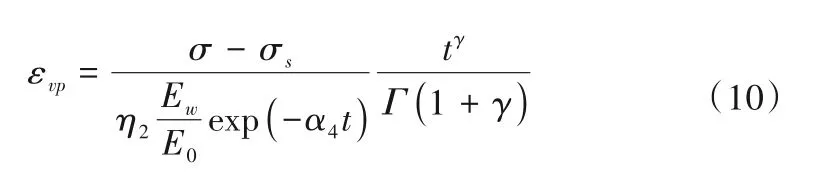
根据文献［15-17］可知，分数阶阶数可表示为与时间损伤变量和含水损伤变量有关的变量

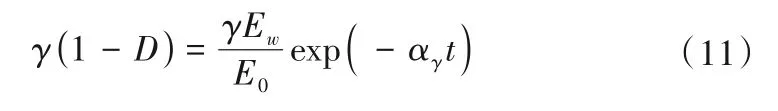
式中：αγ为分数阶阶数的损伤系数。

将式（11）代入到式（10），得：

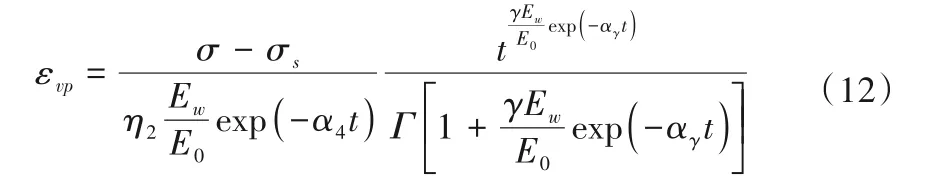
1.3 非定常黏弹性应变确定

传统西原模型中黏弹性参数考虑时间效应，转换为含含水率与时间损伤变量的形式为：

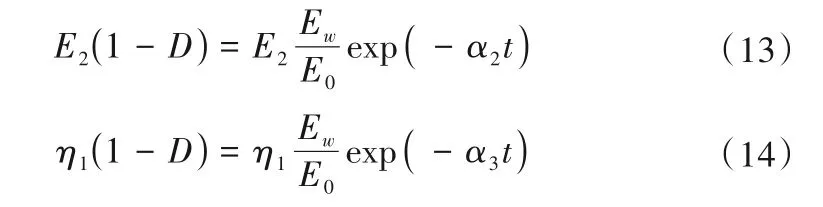
式中：α2为黏弹性弹簧元件的损伤系数；α3为黏弹性黏壶元件的损伤系数。

黏弹性元件的本构方程：

为求解方便，此处认为α2=α3，则得到：

对式（15）进行求解，得：

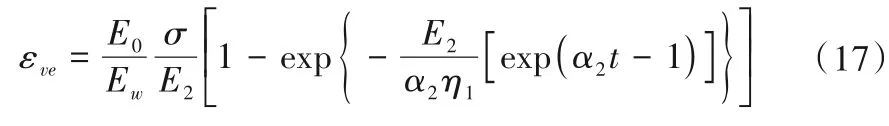
1.4 非定常弹性应变确定

根据文献［18］可知，含水岩石弹性模量与应力满足：

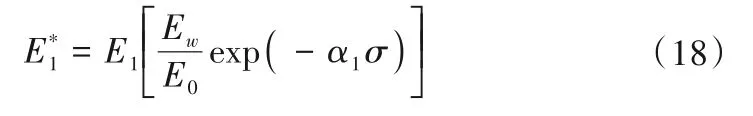
式中：σ为应力。

则胡克元件的弹性应变εe为：

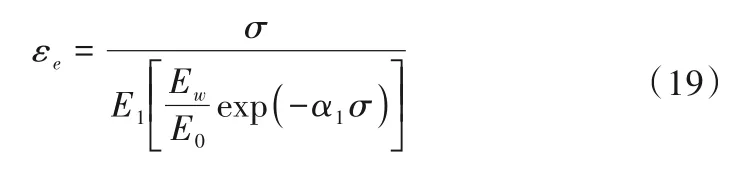
1.5 一维非定常模型建立

总应变ε将满足如下条件：

式中：εe为弹性应变；εve为黏弹性应变；εvp为黏塑性应变。

将式（12）、（17）和（19）代入到式（20），得到：

当σ＜σs时：

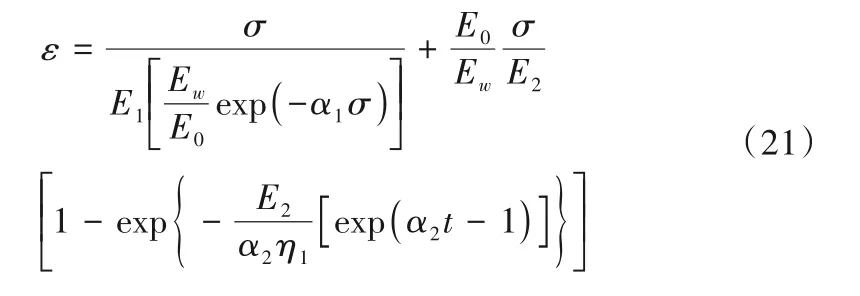
当σ≥σs时：

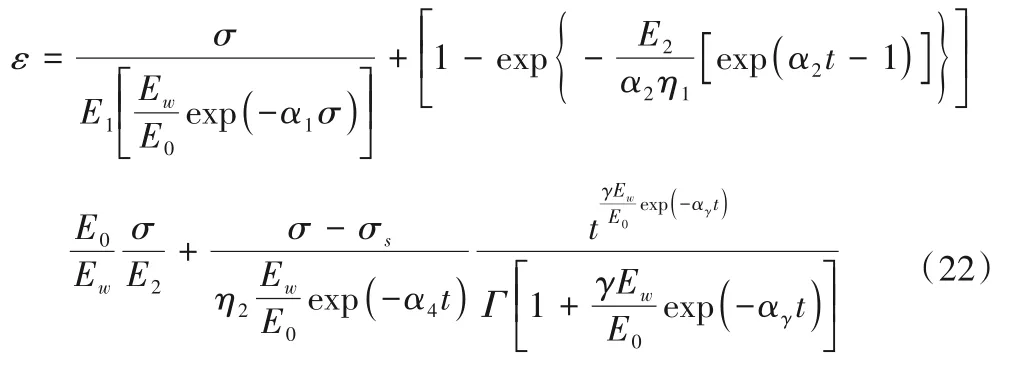
2 室内蠕变试验

2.1 试验准备

试验所用岩石取自全州某引水隧洞围岩（砂岩），岩样质地坚硬，粒径均匀，表面无明显节理，自然状态下呈灰色，干密度为2.19～2.31 g/cm3。按照国际岩石力学学会的标准将岩石制成直径为50 mm、高度为100 mm 圆柱体，将试样置于110 ℃烘干箱中烘烤24 h 后置于干燥箱中冷却至常温，将该状态下岩石的含水率定为0。将岩样浸泡在蒸馏水中进行浸水试验获得不同含水率岩样，跟据浸水试验结果：岩样浸水时间t=0时，含水率w=0%；t=1 h 时，含水率w=0.58%；t=3 h 时，含水率w=1.14%；t=12 h时，w=2.34%；t=62 h时，含水率w=4.73%。

2.2 单轴压缩试验

试验均在中国科学院武汉岩土力学研究所与桂林理工大学土木与建筑工程学院联合研制的全自动三轴试验系统完成，见图3。

图3 全自动三轴试验系统Fig.3 Automatic triaxial test system

蠕变试验加载方式为采用单试件逐级加载的方法［19］。为使蠕变试验加载参数更为合理，对干燥岩样（w=0%）进行单轴压缩试验，根据单轴应力-应变曲线图4，选取蠕变试验第一级应力水平为40 MPa，分级加载以10 MPa为一级。

图4 单轴应力-应变Fig.4 Uniaxial stress-strain

2.3 蠕变试验

采用Bozltmen 叠加法对蠕变试验数据进行处理，绘制不同含水率条件下岩石的单轴轴向蠕变历时曲线如图5所示。

如图5所示，不同含水率岩样蠕变变形规律基本相似，加载后均产生衰减蠕变，等速蠕变，且在最后一级应力水平下产生加速蠕变，但不同含水率岩样变形量间存在较大差别，以40 MPa 应力水平下岩样变形为例，含水率为0、0.58%、1.14%、2.34%和4.73%岩样的瞬时应变分别为2.39×10-3、2.69×10-3、3.21×10-3、3.67×10-3、3.82×10-3，蠕 变 应 变 分 别 为1.12×10-4、1.66×10-4、2.23×10-4、2.79×10-4、4.37×10-4。岩样的瞬时应变与蠕变应变均随含水率上升而逐渐增大。这是可能是由于水的侵蚀使砂岩试样内部颗粒软化，导致胶结程度下降，从而产生更大变形，含水率越大对岩样的软化作用越强，故随含水率增大岩样变形量逐渐上升。

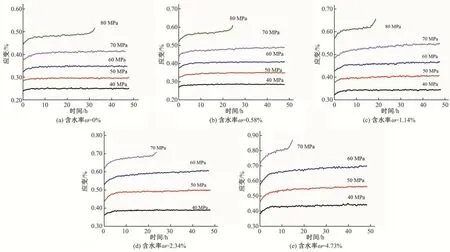
图5 轴向蠕变历时曲线Fig.5 Axialcreep duration curve

3 模型参数确定与模型验证

不同含水率的岩样的弹性模量值经过切线法计算得到，含水率为0、0.58、1.14、2.34和4.73%时，岩样的弹性模量为30.82、29.74、28.79、27.49 和26.29 GPa，对应的含水损伤变量为0、0.035、0.066、0.108和0.147。以含水率ω=0.58%为例，根据等时应力-应变曲线方法（如图6），确定出岩石的长期强度的为σs=60 MPa。

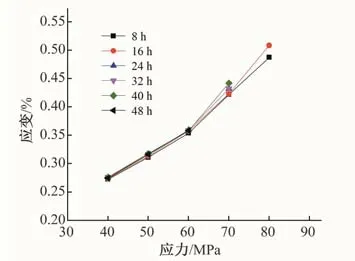
图6 等时应力应变曲线Fig.6 Isochronous stress-strain curve

采用最小二乘法确定不同应力水平作用下岩石模型参数见表1。

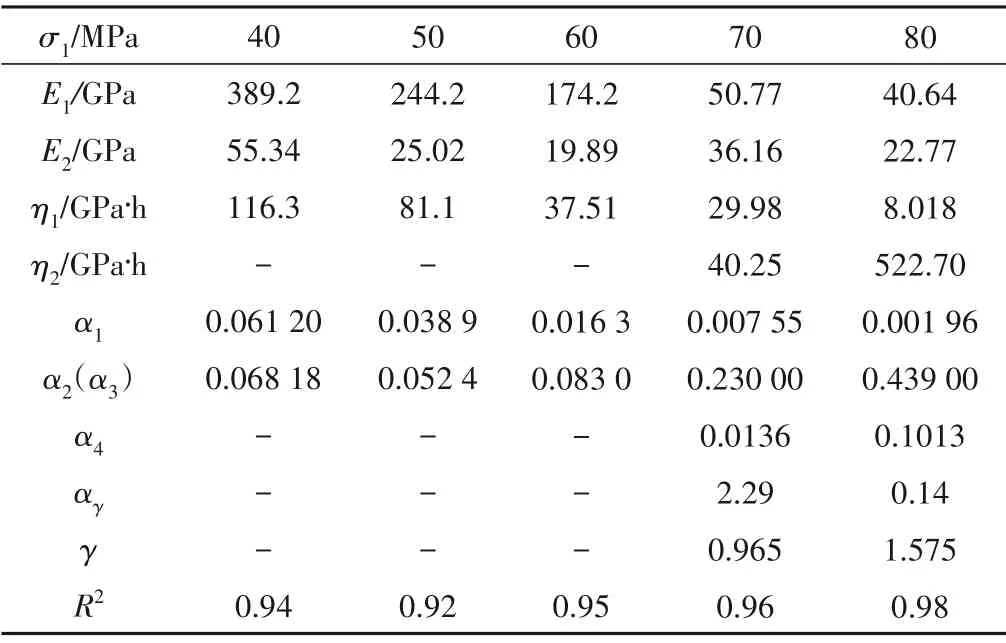
表1 模型参数拟合Tab.1 Fitting of model parameters

将蠕变参数代入到式（21）中，绘制出模型曲线与试验数据对比，得到模型计算蠕变曲线如图7。

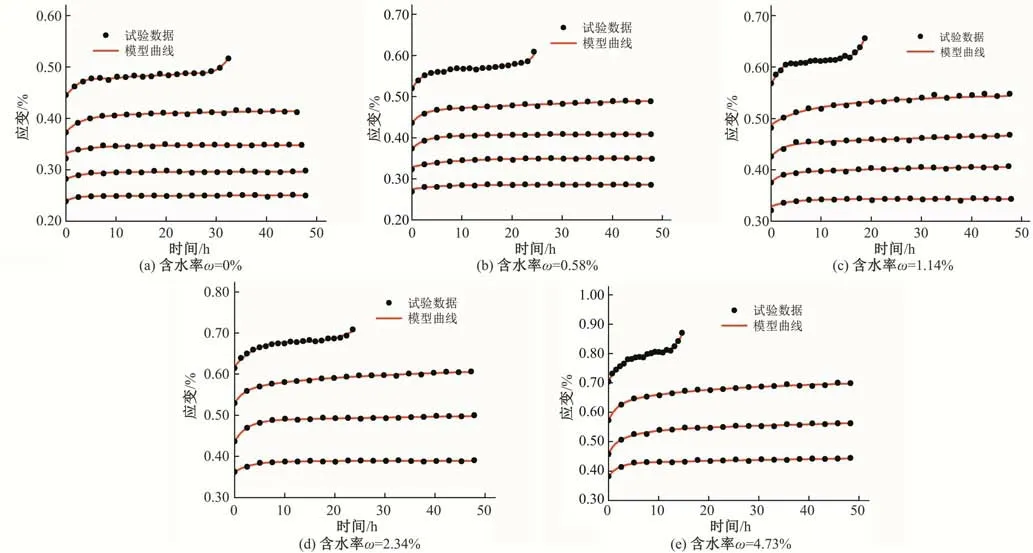
图7 模型与试验数据对比Fig.7 Comparisons between model and experimental data

由图7 可知，模型曲线和拟合良好的吻合度可以充分地说明该损伤模型来反映不同含水率岩石蠕变全过程变形规律是合适可行的，它不仅准确地反映衰减和稳定蠕变阶段的蠕变特性，克服了传统西原体难以描述加速蠕变的缺点，也在一定程度上反映了不同含水率条件下岩石的损伤程度。

从拟合结果可知，建立的损伤蠕变本构模型比西原模型拟合结果要好，但也比西原模型采用更多的参数，所以在此分析含水率ω=0.58%下损伤时效性参数变化规律如图8所示。

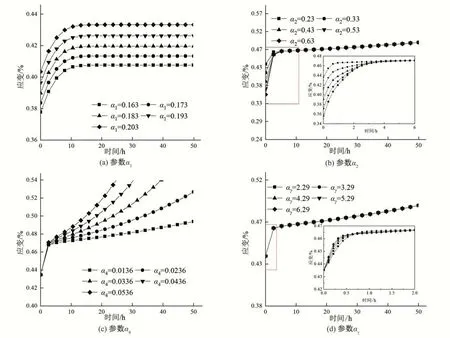
图8 参数敏感性分析Fig.8 Sensitivity analysis of parameters

由图7可知，参数α1主要控制了岩石的瞬时应变值的大小，即随着参数α1值不断增大，岩石的瞬时应变值就越大。参数α2作为控制岩石黏弹性变形和速率的变量，随着该参数值不断增大，岩石在蠕变过程中的黏弹性变形值和变形速率值也就越大。参数α4控制了黏塑性蠕变速率，随着参数α4值的增大，岩石的黏塑性蠕变速率就越大。参数αγ主要作用是在黏塑性黏壶发生作用时，对黏弹性变形向黏塑性变形转化的速率进行修正，保持模型曲线的准确性，随参数越大变形速率越大。

4 结 论

对浸水后全州隧洞围岩开展单轴逐级加载蠕变试验，分析了岩样在不同含水率影响下的蠕变变形规律，并构建了一种考虑在含水率和时间双重影响的新型的非定常分数阶蠕变模型，对试验结果进行了拟合。主要得到以下结论。

（1）在不同含水率作用下，砂岩试样受载后的瞬时变形与蠕变变形量均随含水率的增加逐渐增大。

（2）建立的蠕变模型较好地反映了蠕变参数受含水率和加载应力作用下随时间的劣化性，准确地描述不同应力状态下全州引水隧洞围岩的蠕变损伤过程。

（3）参数α1主要控制了岩石的瞬时应变值的大小，即随着参数α1值不断增大，岩石的瞬时应变值就越大。参数α2作为控制岩石黏弹性变形和速率的变量，随着该参数值不断增大，岩石在蠕变过程中的黏弹性变形值和变形速率值也就越大。

（4）参数α4控制了黏塑性蠕变速率，随着参数α4值的增大，岩石的黏塑性蠕变速率就越大。参数αγ主要是修正在黏塑性黏壶发生作用时，对黏弹性变形向黏塑性变形转化的速率进行修正，保持模型曲线的准确性，随参数越大变形速率越大。