侧槽底坡变化对侧堰淹没度影响研究

周鑫宇，邱 勇，吴锦钢，谢红英，周 艺

（云南农业大学水利学院，昆明 650201）

0 引 言

侧槽溢洪道常应用于岸坡陡峻、无适宜地形设置正槽溢洪道的水利工程中，其溢流堰大致沿等高线布置，具有较长的溢流前缘长度、能更好的降低泄洪水头［1］。在进行侧槽体型设计时，常常以侧槽首端水面高程不超过堰顶水深的一半来保证整个溢流堰为自由泄流［2］。现有文献多针对自由泄流下的侧槽溢洪道进行研究：如陈振军［3］、陈小威［4］、刘发智［5］等对侧槽溢洪道水力特性进行了数值模拟，得到的结果与试验数据相吻合；彭依云［6］等研究了侧槽段螺旋流中气体迁移扩散机理，得出水平向螺旋掺气水流气体运动规律；杨顺玉［7］等通过对侧槽内加设消力墩或者连续升坎，来改善槽后泄槽段水流流态。

近年来，极端气候条件下的暴雨频繁出现，水库遭遇超标准洪水的概率随之提高。考虑到侧槽式溢洪道随堰顶水头增加，其过流能力增幅会出现下降［8］，意味着根据现行规范，即便侧槽式溢洪道能够保证校核流量为自由出流（刚好处于临界状态），其遭遇超标洪水后的超泄能力不足也会给工程安全埋下隐患。

1 模型设计与验证

1.1 物理模型

某水库泄水建筑物为侧槽式溢洪道，其中溢流堰为WES实用堰，堰长L=25 m，上游堰高2.3 m；侧槽横断面形式为窄深式，堰体下游坡比1∶0.6，岸坡侧坡比1∶0.3，槽首底宽2.5 m，槽末底宽5.0 m，底坡1∶250（图1）。侧槽段后紧接20 m 长调整段（i=0）。物理模型按照重力相似准则进行设计，几何比尺λL=36。

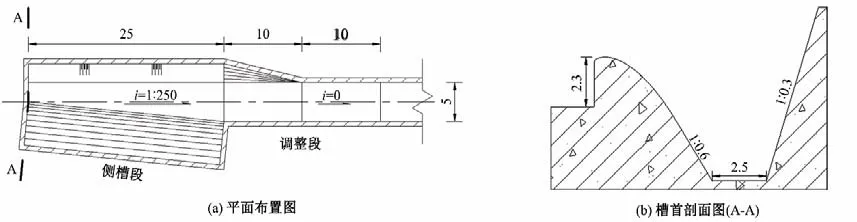
图1 物理模型布置图Fig.1 Physical model layout

1.2 数学模型

数学模型按照实际体型1∶1 建模（图2），采用结构化网格，以侧堰进口段中点为坐标原点，沿侧槽长度方向为y方向，垂直侧堰方向为x方向，铅直方向为z方向，将模型整体划分为两个网格块（图3）。

图2 数学模型Fig.2 Mathematical Model

图3 网格划分示意图Fig.3 Mesh division diagram

网格块A：x方向由侧槽进口（xmin=0）至岸坡侧（xmax=15.5 m），y方向由侧槽首端（ymin=-12.75 m）至侧槽末端（ymax=12.75 m），z方向由底板（zmin=0）至侧槽边墙顶部（zmax=13.5 m）；

网格块B：在x方向尽可能靠近泄槽：xmin=6.5，xmax=15.5 m，y方向从侧槽末端断面（ymin=12.75 m）至调整段末端（ymax=32.75 m），z方向与网格块A相同（zmin=0，zmax=13.5 m），每个网格单元边长为0.18 m，整个计算域网格数量约为830万。

为了更好的模拟水库库水位，在模型上游添加自然水域，高度为堰顶高程，进口边界采用流量进口，出口边界采用压力出口，壁面均为对称边界；紊流模型采用RNGk-ε模型，气液自由表面追踪采用TruVOF方法［9-11］。

研究方案考虑了5 种侧槽底坡i=0、0.004（物理模型底坡）和0.02、0.04、0.06，流量采用以下6组：Q=90、100、110、120、130、140 m3/s。

1.3 模型验证

对底坡为i=0.004的侧槽进行数值模拟计算，得到不同流量～水位关系（图4）。

图4 试验研究水位～流量关系图Fig.4 Test study of water level～flow rate relationship

由图4 可以看出，数值计算结果与模型试验最大误差不超过2%。在Q=120 m3/s下的流态对比如图5、6所示。

由图5（a）可以明显看到，在物理模型试验中，侧槽内过堰水舌掺气后在侧槽轴线附近形成顺时针旋转螺旋流，沿侧槽抖动前行，形状沿水流方向由细到粗；在图5（b）数值计算中，流速矢量沿侧堰边界潜入槽底，并在边墙阻挡下向上翻卷形成螺旋流，与试验流态基本吻合。

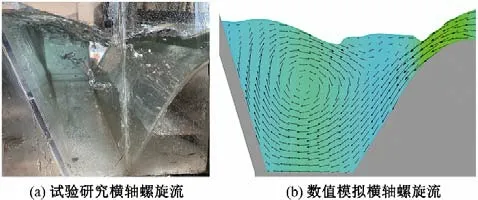
图5 侧槽横轴螺旋流Fig.5 Side channel of cross-axis spiral flow

由图6可以看出，过堰水流在侧槽内形成翻卷，使得岸坡侧水面壅高，翻卷回淹水流与过堰水舌之间形成倒三角状水流，数值计算所得到的流态与试验研究是吻合的。

图6 侧槽水面流态图Fig.6 Side channel water surface flow pattern

2 数值模拟成果

2.1 侧堰过流能力

通过模拟计算，得到不同底坡条件下，侧槽溢洪道的过流能力（图7）。

由图7可以发现，不同底坡下，水位流量关系曲线上均出现一个拐点，使得库水位上升趋势由平缓变得陡峻，并且底坡越大，拐点出现越早。拐点的出现意味着侧槽内水流开始对侧堰形成顶托，致使库水位壅高明显，表明侧槽溢洪道遭遇超标准洪水时，超泄能力下降，可能危及水库枢纽工程防洪安全。

图7 数值模拟水位～流量关系图Fig.7 Numerical simulation of water level ～flow rate relationship

根据模拟计算，得到侧槽溢洪道侧堰考虑淹没系数σs影响的综合流量系数M（M=σsm），详见表1。

由表1可以看出，对于不同底坡的侧槽，考虑淹没系数影响的综合流量系数均表现为先增大后减小的趋势。此外，当底坡i=0 时，最大综合流量系数M=0.507；随着底坡的增加（i=0.02），最大综合流量系数M下降为0.489，降幅为3.55%；当底坡增加至i=0.04 时，最大综合流量系数M下降为0.462，降幅增加至5.52%，当底坡进一步增加至i=0.06 时，最大综合流量系数M仅为0.435，降幅为5.84%，表明底坡的增加，导致侧槽首端水深被抬高，使得侧堰淹没度增大，过流能力降低明显；与此同时淹没发生的临界流量值下降：侧槽纵坡不变时（i=0），拐点处对应流量为113.95 m3/s；但随着底坡增大到0.02、0.04 和0.06，拐点对应流量相继减小为112.86、111.46、109.43 m3/s，亦即底坡增量不变，但拐点流量降幅却逐渐增加，由0.96%、1.20%增大至1.80%。

表1 不同底坡下的侧堰过流能力Tab.1 Flow capacity of side weirs under different bottom slopes

2.2 侧槽淹没度

侧槽溢洪道往往有着较长的溢流前缘长度，即使侧槽首端水位已经对溢流堰产生淹没，但就全堰来看，对过流能力的影响尚未显现，这时的淹没度称为临界淹没度。根据各底坡情况下流量变化拐点所对应的侧堰沿程临界淹没度（图8）、槽首临界淹没度，通过实用堰淹没系数图［12］查得与之对应的淹没系数（图9）。

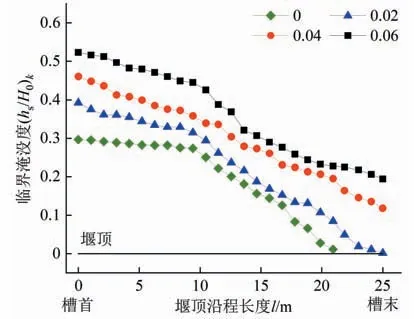
图8 不同底坡下的侧堰沿程临界淹没度Fig.8 Critical submergence degree along side weirs with different bottom slopes

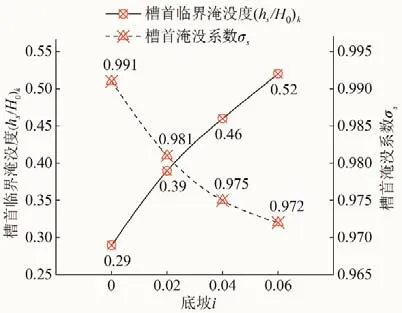
图9 不同底坡下的侧堰槽首临界淹没度与淹没系数Fig.9 Critical submergence degree and submergence coefficient of side weir head under different bottom slopes

由图8和图9可以发现，底坡为平坡（i=0）时，流量增幅趋缓时的淹没度在侧槽首端为0.29，但沿侧堰长度方向依次递减：在距离侧槽末端3.14 m处，槽内水深低于堰顶，不再形成淹没。

随着底坡由i=0.02 增大至i=0.06，尽管拐点流量值在下降，但侧槽首端淹没度依然由0.39 增加至0.52，且侧堰已呈全部淹没状（侧槽末端淹没度由0.004 上升至0.19），侧堰淹没系数也由0.991（i=0）下降为0.972（i=0.06）。

2.3 侧堰长度变化对淹没度的影响

2.3.1 堰长变化的影响（底坡不变）

在实际应用时难免会遇到侧槽首端底板高程无法满足开挖深度的情况，此时，若抬升底板高程，会使得槽首形成淹没，导致库水位壅高，危及水库枢纽防洪安全。考虑到侧堰常沿等高线布置，可以通过适当延长侧堰长度，改善其淹没长度来降低堰顶水头。

在流量Q=120 m3/s，并保持侧槽首端与末端底板高差Δz=0 m（i=0）的情况下，延长侧堰长度，分别得到侧槽沿程堰顶水头和槽首淹没度变化情况如图10和图11所示。

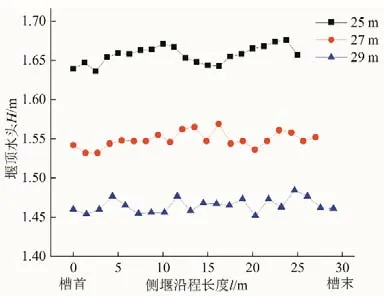
图10 侧堰长度变化情况下的堰顶水面线（i=0）Fig.10 Water surface line at the top of the weir for the case of changing length of the side weir（i=0）

图11 侧堰长度对槽首淹没度与淹没系数的影响（i=0）Fig.11 Effect of side weir length on the submergence degree and submergence coefficient of the channel head（i=0）

由图10 可以看出，侧槽（底坡i=0）堰顶水面线沿侧槽长度方向均呈波动状，但堰顶水头降幅随侧堰长度增加而减小：堰长L=25 m时，堰顶平均水头1.657 m；堰长增加到27、29 m，堰顶平均水头下降到1.549 m（降幅6.5%）和1.465 m（降幅5.4%）。

由图11可以看出，堰长增加，槽首淹没系数逐渐增大（淹没度下降），但增幅减小（由1.5%减小至0.5%），淹没系数变化曲线呈“凸”型。

保持侧槽首端与末端底板高差不变，延长侧堰长度，能有效降低侧槽溢洪道淹没度（增大综合流量系数），同时降低堰顶水头。

2.3.2 堰长变化的影响（底坡增大）

当流量Q=120 m3/s 时，增加侧槽首端与末端底板高差（同步增加侧堰长度），得到侧槽沿程堰顶水头和槽首淹没度变化情况如图12和图13所示。

由图12可以发现，同时增大侧槽首端与末端底板高差与侧堰长度，堰顶平均水头呈下降趋势（由1.657 m 下降为1.584、1.473 m），且降幅逐渐增大（4.4%增加至7.1%），表明堰长增加效果明显。

图12 底坡及侧堰长度变化情况下的堰顶水面线Fig.12 Water surface line at the top of the weir for changes in bottom slope and side weir length

由图13 可以看出，随着侧槽首端与末端底板高差的增大（同步增加侧堰长度），侧堰槽首淹没系数曲线变化由缓到陡，增幅逐渐增大（0.6%→1.1%），曲线近呈“凹”型。

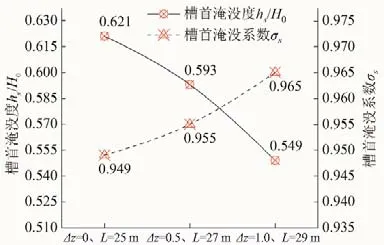
图13 底坡及侧堰长度对槽首淹没度与淹没系数的影响Fig.13 Effect of bottom slope and side weir length on the submergence degree and submergence coefficient of the channel head

2.3.3 侧槽首、末底板高差与堰长的关系

通过抬高槽首底板高程，增大底坡，客观上使得溢流堰堰顶水位壅高；保持侧槽首端与末端高差不变，延长侧堰长度，有利于降低堰顶水头。

若在增大侧槽首、末底板高差的同时，延长侧堰长度，便可在相同来流条件下保证侧堰的自由出流。对此，通过模拟计算得到保持堰顶水头不变的侧槽首、末底板高差Δz与堰长L的关系如表2所示。

表2 侧槽首、末底板高差Δz～堰长L关系表Tab.2 Relationship between the height difference Δz of the head and end bottom slopes of the side channel and the length L of the weir

对表2数据进行公式拟合，得到相关系数为0.97的侧槽首、末底板高差Δz与堰长L关系式如下：

式中：L为计算堰长，m；L0为初始堰长，m；Δz为侧槽首、末底板高差，m。

在进行侧槽设计时，可在公式（1）计算结果的基础上适当增加侧堰长度，以避免由于槽首淹没原因所导致的溢洪道超泄能力不足。

3 结 论

通过研究侧槽不同底坡变化对溢洪道侧堰过流能力、槽首临界淹没度以及槽首、末底板高差与堰长之间相互变化关系，得到如下成果：

（1）不同底坡（i=0、0.02、0.04、0.06）下，水位-流量关系曲线上均存在由缓到陡的拐点：侧堰过流能力增幅先增大，后减小。底坡为平坡（i=0）时，槽首临界淹没度仅为0.29（淹没系数0.99）；随着底坡增大，槽首临界淹没度逐渐由0.39（i=0.02）、0.46（i=0.04）增加至0.52（i=0.06），淹没系数由0.991 减小至0.972。说明单纯加大侧槽底坡，会导致侧槽溢洪道淹没度增加，降低侧堰过流能力。

（2）在保持侧槽首、末两端底板高差不变的情况下，适当增加侧堰长度，有利于降低堰顶水头和槽首淹没度；或者可以通过增加侧堰长度，抵消侧槽首、末底板高差Δz增大的负面影响，使得侧槽溢洪道在不改变来流条件的情况下，维持原设计库水位。

为了避免侧槽式溢洪道在下泄超过校核流量的洪水时，超泄能力不足，可适当增加按照拟合公式计算得到的侧堰长度。