固定导叶数对混流式水轮机水力波动影响分析

徐良玉，郭俊勋，顾承庆，厉洪祥，周大庆，程永光，郑 源，阚 阚

（1.国网新源水电有限公司新安江水力发电厂，杭州 311699；2.河海大学水利水电学院，南京 210024；3.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

0 引 言

水力扰动往往是大型旋转水力机械结构振动的主要激振源［1］。我国许多大型水电机组都存在不同程度的水力激振现象，严重的会导致机组出现非正常振动［2］，缩短了机组检修周期，影响机组的稳定运行和经济效益。因此，研究水轮发电机组内部流场与结构振动特性具有重要意义。

学者及工程师们针对机组的水力波动问题的不良影响进行了多方位研究，其中不乏许多具有针对性的解决方案。如唐拥军等通过有限元分析发现张河湾抽蓄电站的过大振动与导叶间的压力脉动有关，对转轮进行水力优化后大大缓解了振动及噪声的问题［3］。杨梦起等及李佳楠等以电站为研究对象，用现场试验及数值模拟的方式证明了采用长短叶片的转轮设计可以有效降低无叶区压力脉动幅值，使得电站的振动性能得以改善［4，5］。

水轮机中水流的压力脉动往往成为了众多学者研究的热门方向。随着科学技术的进步，数值模拟方法的运用也越来越广泛，学者也对水体压力脉动［6］对机组振动［7］的影响做了许多工作，崔秋雯通过对比不同导叶开度、不同单位转速及变流量的边界条件，寻求各种工况条件下的压力脉动分布特点及传播规律［8］。Chirag Trivedi 等通过对两台混流式水轮机模型的试验研究，探究其压力脉动幅值在工况变化时的变化规律，展现了同步与非同步压力脉动幅值之间的差距［9］。汪昊蓝等通过研究混流式水轮机内部若干个监测点的数值模拟结果，展示了混流式水轮机内压力脉动主要受叶片通过频率的影响，以及不同的导叶开度对压力脉动的分布及大小影响状况［10］。而水轮机稳定性的研究包括多种因素的共同作用。前人也有对机组稳定性的研究做了一些总结。桂中华等总结了国内外水轮机压力脉动与水力稳定性模型试验、水轮机压力脉动与振动数值模拟以及水轮机转轮动应力与叶片振动研究方面的最新成果［11］。徐连琛等总结了国内外研究人员对压力脉动在无叶区引起的结构振动及其研究方法，同时也介绍了抑制无叶区压力脉动的若干方法成果［12］。

有许多电站为了节约建设资金，采用半数固定导叶的安装方式，如24 只固定导叶改成12 只固定导叶的形式，前人的研究中鲜有提及导叶数量对水轮机机组振动特性的影响，以新安江电站某两台12 只固定导叶机组出现振动异常对比同电站其余24只固定导叶数机组进行三维数值模拟，探求固定导叶数对机组水力性能的具体影响，为解决机组不稳定性的研究提供参考。

1 计算模型

1.1 模型及网格

根据已有资料，建立混流式水轮机模型。计算体包括蜗壳、导叶、转轮、尾水管，为了便于计算，构建一段蜗壳进口输水管道与尾水管出口管道。新安江电站某台机组的主要参数见表1，混流式水轮机整体模型如图1所示。

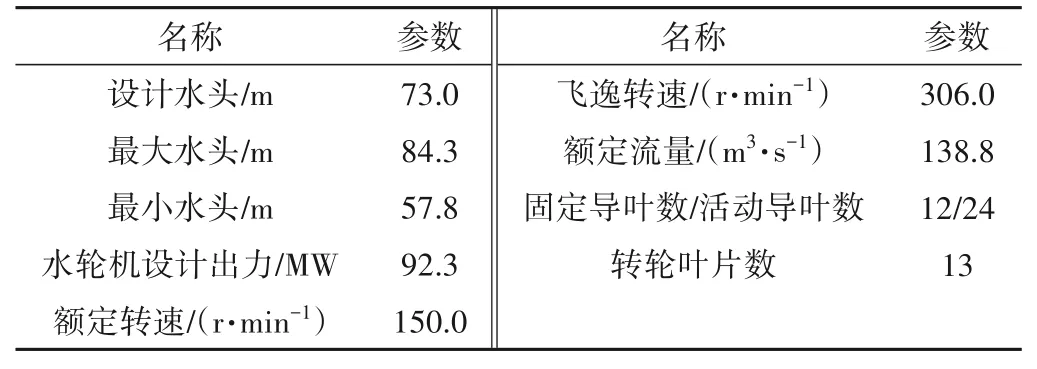
表1 混流式水轮机机组参数表Tab.1 Parameters of the Francis turbine unit

图1 混流式水轮机总体模型Fig.1 Overall model of the Francis turbine

1.2 网格划分

混流式水轮机机组三维几何模型皆采用ICEM 软件对其进行网格划分。流体域中的网格划分全部采用结构化网格的划分方式。通过网格独立性验证，最终确定各部分网格数量约536万，各部分网格划分如图2。

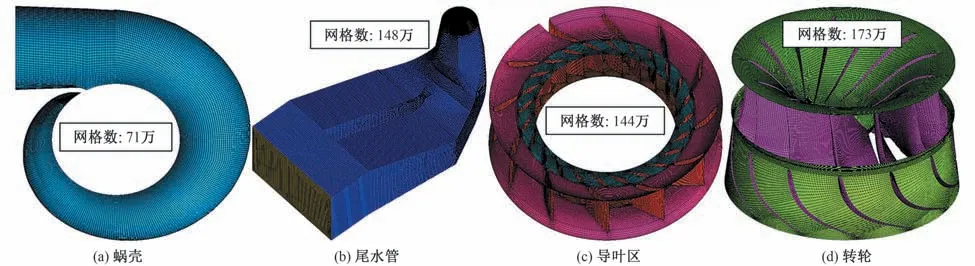
图2 网格划分Fig.2 Meshing

1.3 边界条件设定

计算采用商业软件ANSYS FLUENT 19.2。湍流模型选用RNGk-ε湍流模型，采用自动壁面函数。将固壁面设置为无滑移壁面，数值计算精度设置为10-5。边界条件：蜗壳进口和尾水管出口处均设为压力边界；各计算区域之间通过interface 进行数据交换。活动导叶开度根据计算工况需求设定。稳态计算时，转轮区域采用多重参考坐标系（MRF）方法模拟，在非稳态计算时，采用滑移网格（Sliding Mesh）方法模拟，计算步长取0.003 s，转轮每个步长旋转角度约2.7°。求解过程中，速度场和压力场的解耦采用SIMPLEC 算法，时间和空间的插值精度均采用二阶精度。

1.4 验证工况及精度评价

为了进一步验证混流式水轮机数值模拟结果的准确性，选取电站2021年12月份某机组甩负荷试验报告，计算工况以试验进行时的水头77.25 m为边界条件，计算了试验中的4组经典工况进行对比。CFD 模拟时给定压力进口与压力出口边界条件。

模型可靠性验证：模拟的4 组工况与试验工况保持相同的导叶开度，对比其负荷的大小，如表2 所示，所有工况误差均小于5%，计算精度满足要求。

表2 稳态工况CFD结果与试验对比Tab.2 Comparison of CFD results and test results under steady condition

CFD模拟计算不同导叶开度的4个工况点的结果见表3。

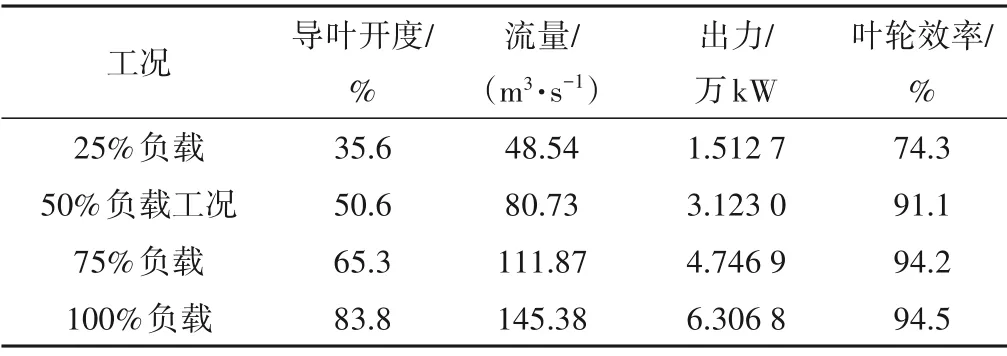
表3 定常计算结果Tab.3 Result of steady calculation

2 结果与分析

2.1 计算说明

流体对转轮的激振力也是影响机组稳定性的重要因素，为此基于新安江电站4、6 号机组采用12 只固定导叶与其他机组24 只固定导叶的区别上进行研究，如图3 为两种导叶数量的模型图对比，对两种模型在100%负载工况下的计算进行对比，计算中所有的边界条件均一致。整个轴系的振动与转轮的受力密不可分，所以计算对比主要针对转轮的各种力学参数，为了更方便对比，所有力学参数均进行了归零化处理，即计算值减去平均值。

图3 固定导叶模型对比Fig.3 Comparison of fixed guide vane models

2.2 导叶区流场对比

转轮处的水力扰动与其距离最近的活动导叶这一过流部件密切相关，因此，分析不同固定导叶数布置对活动导叶区的流态的影响如图4，其中活动导叶的压力分布仅在迎水面的尾部区域略有不同如图中红圈区域，在活动导叶出口处压力分布几乎一致；在理论上固定导叶的减少将增加过流面积，影响径向流速，而由速度分布对比图可以看出，在相同的压力边界条件下，导叶区的流速在大小和分布上接近一致，说明转轮区的水力扰动与来流流速关系不大。

图4 导叶区压力与流速分布对比图Fig.4 Comparison diagram of pressure and velocity distribution in guide vane region

如图5 为导叶区的局部流态图，不同固定导叶数布置对活动导叶区的影响除了速度矢量近乎一致外，还需关注到涡量分布的不同，图5 中的红色涡量为level 值0.03 下的Q 准则生成活动导叶区的涡量，对比可知活动导叶区在该水平值下的涡量主要发生在流道靠近顶盖和导叶迎水面的位置，图5 中红圈的对比可以看出较少固定导叶数布置的工况出现的涡量更多，表明水力扰动更大。

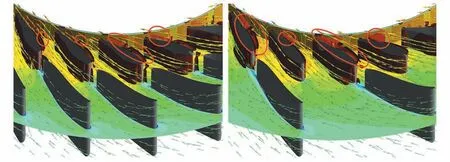
图5 导叶区流态及涡量对比图Fig.5 Comparison of flow pattern and vorticity in guide vane region

2.3 转轮力学特性分析

图6 为不同固定导叶数机组的转轮力矩波动对比图，可以看出较少固定导叶数的力矩波动明显高于24叶固定导叶，观察图7 两种导叶数的力矩频谱分析对比图验证了这一观点，首先力矩频谱图除去了10 Hz以下的低频脉动成分，研究10～120 Hz间的主要脉动点，其中主频为32.5 Hz 为转轮的叶片通过频率，在所有边界条件相同的前提下，通过对比可以得出12只固定导叶的力矩在转轮叶片通过频率的振动幅值是24 只固定导叶的4.83 倍；在同样拥有24 只活动导叶的前提下，固定导叶数量的减半使得导叶和转轮间动静干涉的作用加强，使12只固定导叶出现了小幅度的2倍转轮叶片通过频率（65 Hz），而该频率是厂房振动问题的高发频率［13］。

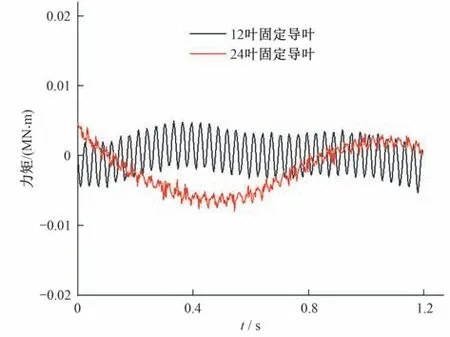
图6 固定导叶数对转轮力矩波动的对比图Fig.6 Influence of guide vane number on torque fluctuation of runner

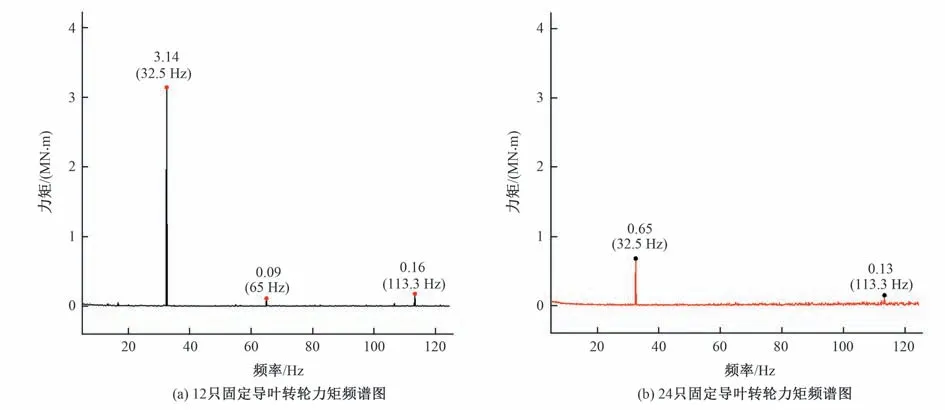
图7 两种导叶数的转轮力矩频谱分析对比图Fig.7 Comparison of torque spectrum analysis of two guide vane numbers

如图8，由两种固定导叶数量下的转轮升力和阻力对比中可以看出，其转轮叶片通过频率的振动幅度差距不大，但24 只固定导叶数在单位时间内振动次数更多即高频成分更明显。

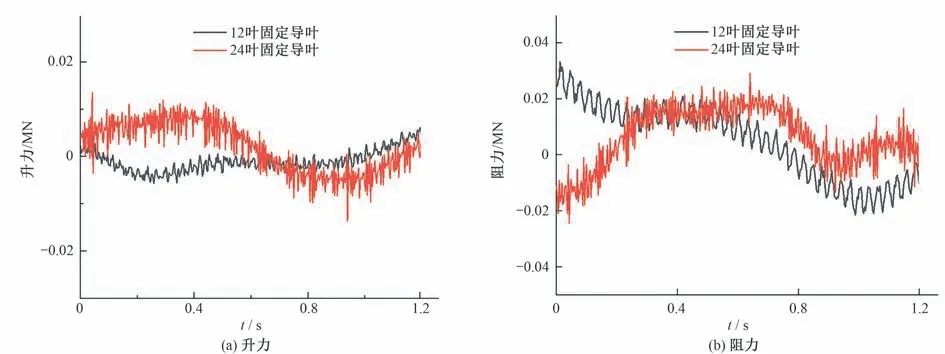
图8 不同导叶数的转轮升力/阻力波动对比图Fig.8 Contrast diagram of lift/drag fluctuation of runner with different guide vane numbers

机组中转轮和主轴振动的大小主要是水流对转轮产生的径向力的作用为主导因素，因此如图9 为水轮机叶轮整体受水流作用的X、Y方向径向力经过归零化处理后的对比，在相同的边界条件下，计算得到的径向力其整体的变化趋势基本一致，但明显可以看出24只固定导叶的高频波动更小；通过对径向力的频谱分析，如图10 中12 只固定导叶的X方向径向力在32.5 Hz 时的振幅是24 只固定导叶的2.75 倍，而12 只固定导叶的Y方向径向力在32.5 Hz 时的振幅是24 只固定导叶的4.63 倍，同样12 只固定导叶在径向力上也表现出2 倍转轮叶片通过频率（65 Hz）振动幅度的加强效应。

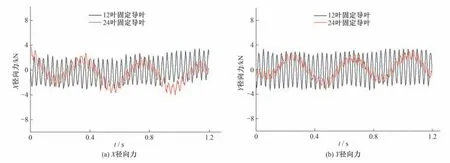
图9 不同导叶数的转轮X径向力/Y径向力波动对比图Fig.9 X radial force/Y radial force fluctuation of runner with different guide vane numbers

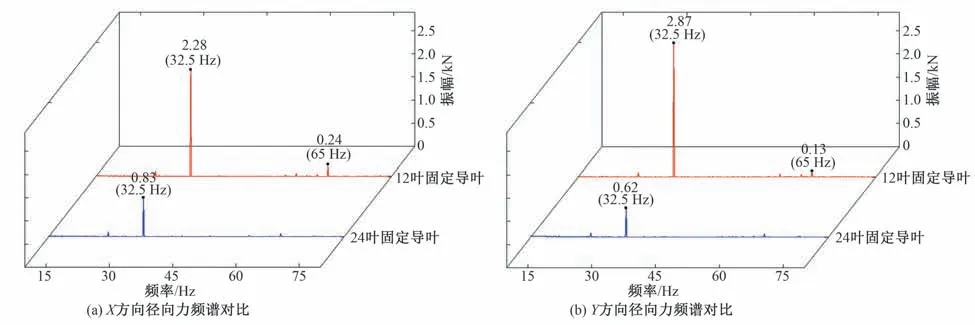
图10 转轮X径向力频谱分析对比图/转轮Y径向力频谱分析对比图Fig.10 Comparison diagram of X-radial force/Y radial force spectrum analysis of runner

3 结 论

以国内某大型混流式水轮发电机组为原型，通过全流道三维数值模拟，并以额定工况点为基准，对所建立的模型进行计算验证，结果验证了计算模型的准确性与可靠性，同时也针对不同的固定导叶数量对流场的影响进行了研究，结果表明。

（1）相同压力边界条件下，固定导叶数的差异对转轮进口流速影响不大，更多的固定导叶数降低了涡量的分布，而活动导叶区涡量的差异主要发生在流道靠近顶盖和导叶迎水面的位置。

（2）在相同边界条件下，半数固定导叶数的机组转轮的升力和阻力波动差距并不明显，而力矩的波动幅值存在明显的倍数关系，12只固定导叶的机组力矩波动频率处于转轮叶片通过频率（32 Hz）时，其幅值是24只时的4.83倍。

（3）转轮振动最根本的来源是水流对它的作用力，更少的固定导叶数量会明显加剧这种作用力的不稳定性，而1 倍叶片通频时，12只相比24只固定导叶拥有2.75倍的X径向力振幅和4.63 倍的Y径向力振幅；在同样拥有24 只活动导叶的前提下，固定导叶数量的减半使得导叶和转轮间动静干涉的作用加强，使12只固定导叶出现了小幅度的65 Hz振动即2倍的转轮叶片通过频率。