基于修正形函数的Euler-Bernoulli开口裂纹梁单元刚度矩阵

徐 训，朱亚杉，吴 浩

(武汉理工大学 土木工程与建筑学院，武汉 430070)

裂纹是土木工程结构最常见的损伤形式，裂纹会造成结构局部刚度降低，影响结构的动力特性。带裂纹构件的受力特性可采用有限元软件进行研究，如ABAQUS常用无厚度的Cohesive单元对裂纹进行模拟[1-2]，也可用指派裂纹或VCCT(virtual crack closure technique)等方法进行裂纹模拟[3-4]，上述方法在裂纹处需要进行网格加密以适应裂纹尖端应力场的奇异性，这将大幅增加计算自由度。工程中以结构固有频率或模型修正等为代表的损伤识别方法要求裂纹模型能准确的描述损伤特性[5-7]，并具有模型简单、参数少的特点。因此，以结构损伤识别为导向的裂纹梁有限元建模问题仍然是充满挑战的课题。

裂纹单元刚度矩阵的建立是有限元分析的关键。目前裂纹单元刚度建立方法主要包括基于应变能释放的方法和传统方法。在基于应变能释放的方法中，裂纹产生的弹性应变能被加到非裂纹单元的弹性应变能中[8]，单元刚度矩阵可采用柔度计算法和直接刚度计算法两种方法。柔度计算法是根据裂纹单元的应变能，应用卡式第二定理先推导柔度矩阵，再通过传递矩阵或直接求逆等方法得到裂纹单元的刚度矩阵，Papadopoulos等[9-11]对一维裂纹梁的刚度进行了研究。此外，文献[12-14]对其在二维有限元中的应用也进行了讨论。直接刚度计算法是直接利用卡式第一定理求得裂纹单元的刚度矩阵，该方法由Potirniche等[15]推导出二维裂纹单元，然后由Hall等[16]推导出带有单边裂纹的三维裂纹单元。Yazdi等[17]充分比较了基于应变能释放的两种方法，他们的研究表明用卡式第一定理生成裂纹单元刚度矩阵的不足之处，也证明了由Potirniche等[16]提出的方法在裂纹宽度较大时可能会导致解出现较大的误差。

传统方法是直接利用刚度折减[18]、单元截面参数折减[19]或弹性模量折减[20]等方法得到裂纹单元刚度矩阵。前者在非裂纹单元刚度矩阵中直接通过折减系数与刚度矩阵的表征裂纹对刚度矩阵的影响，无法表征裂纹深度和位置对刚度矩阵影响。后两者的实质是通过截面惯性矩、弹性模量的变化反映裂纹单元的抗弯刚度的变化，再通过抗弯刚度与形函数的二次导乘积的定积分得到裂纹单元刚度矩阵。如Shen等[21-23]通过指数型函数、阶跃函数来描述抗弯刚度变化，这类方法认为形函数是始终不变的。

事实上，裂纹会影响裂纹附近一定距离的应力场变化，但这一变化不会直观对应构件截面惯性矩的改变。且构件的弹性模量应只与材料相关，折减弹性模量物理意义不明确，则裂纹对单元刚度的影响可认为主要是改变了形函数。本文以Euler-Bernoulli梁为研究对象，在Euler-Bernoulli梁单元中，形函数的物理意义为两端固定梁只产生一个单位位移(或转角)时梁弯曲成的形状[24]。有限元方法中，位移场用形函数和结点位移的乘积表示，裂纹对单元位移场的影响，必然导致裂纹单元形函数的改变。

有限元分析中通常利用位移场的改变去描述形函数的变化。Babuska等[25]利用无裂纹单元形函数的单位分解性质提出了单位分解有限元法，通过附加位移自由度向量描述裂纹单元位移场，裂纹对位移场的影响通过增强函数和无裂纹单元形函数的乘积产生作用[26-27]。值得注意的是，这种方法丢失了常规有限元的插值属性，会把有限元中的边界条件应用复杂化，但增强函数这一概念极大促进了扩展有限元和广义有限元方法的发展[28]。通过增加额外自由度，广义有限元法有效描述了裂纹单元位移场函数变化[29]，并给出了广义形函数的具体形式，但广义有限元法需要设置与局部加强函数数目相等的额外自由度，这种依赖额外自由度的方法会造成线性相关性问题[30]，部分基于增加额外自由度的有限元方法还需考虑单元交界面的连续性问题[31]。针对该问题，Tian等[32]提出了无额外自由度广义有限元法，该方法中结点自由度与标准有限元相同，增强函数直接附加在形函数上。

本文以单边贯穿非扩展Euler-Bernoulli开口裂纹梁为研究对象，本文研究的最终目标是通过修正形函数，再利用抗弯刚度与修正后形函数的二次导乘积最终得到裂纹单元刚度矩阵。首先根据无额外自由度和增强函数的思想得到Euler-Bernoulli裂纹单元位移场，再通过位移场得到裂纹单元的形函数，最后利用虚位移原理导出Euler-Bernoulli裂纹的单元刚度矩阵。本文将讨论裂纹单元形函数的性质和所提单元刚度矩阵的有效性，研究结果将为基于静力分析和振动分析的损伤识别方法提供新的研究思路。

1 Euler-Bernoulli裂纹梁单元位移场函数

单位分解有限元法通过在有限元插值函数中引入不连续函数来考虑裂纹的影响，其位移场函数uh(x)是传统有限元位移场函数uFE(x)和增强位移函数uenh(x)之和[25]，如式(1)所示：

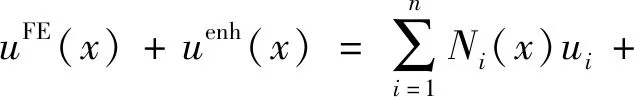
(1)

式中：ui是传统有限元i结点位移自由度向量，Ni(x)是与i结点对应的形函数；ak是附加位移自由度向量，m为增强结点数，ψ(x)是增强k结点形函数的支撑域内的增强函数。Nk(x)是与k结点对应的形函数。利用形函数单位分解的性质，ψ(x)与形函数Nk(x)相乘可以全局或局部表征裂纹对uh(x)的影响。但增强函数ψ(x)依赖于附加自由度ak，附加自由度会导致求解规模增大等问题。针对此问题，Tian等提出了无额外自由度的有限元方法，其位移场函数如式(2)所示。

(2)

上述无额外自由度的有限元方法形函数为NiG(x)=∑Ni(x)∑ψ(x)，而增强函数ψ(x)需要由定义在该结点附近的单元结点进行构造，计算比较复杂。结合单位分解有限元单元增强函数和无额外自由度的想法，本文Euler-Bernoulli梁裂纹单元计算模型如图1所示。

图1中，le代表裂纹单元的长度，x0代表裂纹位置与单元i结点的距离(x0∈[0,le])，a代表裂纹的深度，h代表计算单元高度，b代表计算单元宽度，ui，θi，uj，θj分别代表i，j结点位移和转角，Vi，Mi，Vj，Mj分别代表i，j结点的竖向力和弯矩，假定i，j结点处所示的位移与转角均为正方向，增强函数ψ(x)只“附加”在本单元的i，j结点上，结合冯新等[33-34]的研究，梁单元位移场uh(x)用式(3)表示。

图1 Euler-Bernoulli梁裂纹单元分析模型Fig.1 Euler-Bernoulli beam crack element analysis model

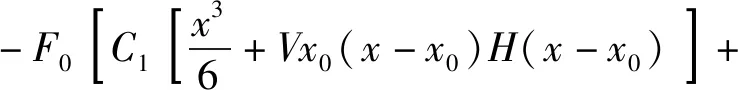
(3)

式中，F0=EI0表征未损伤构件的抗弯刚度，E为弹性模量，I0为完好梁截面的截面惯性矩。式中H(·)为Heaviside函数，C1，C2，C3，C4与梁的边界条件相关。V是表征裂纹深度a的函数，根据文献[33-35]，其具体形式如式(4)所示。

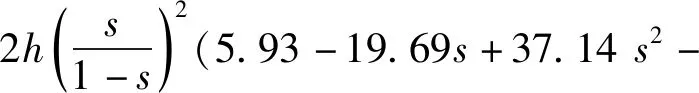
35.84s3+13.125s4)

(4)

式中，s=a/h，代表裂缝深度的归一化参数。

将式(3)转化为Euler-Bernoulli裂纹的挠度表达式如下

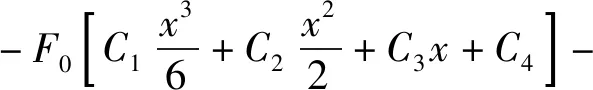
(F0C1Vx0-C2V)xH(x-x0)+

(5)

相较式(3)，式(5)清晰的表明位移场函数uh(x)是传统非裂纹单元位移场Hermitian三次多项式F0(C1x3/6+C2x2/2+C3x+C4)与增强位移函数g(x)= (F0C1Vx0-C2V)xH(x-x0)-(F0C1Vx02-C2Vx0)H(x-x0)之和。可通过修改g(x)以适用多裂纹及更符合裂纹构件工程实际的情形。由式(5)知，如图1所示的单元裂纹左端的位移场用Hermitian三次多项式拟合，而在右端位移场则由Hermitian三次多项式和g(x)共同拟合。g(x)与裂纹位置x0和裂纹深度a均有关系。值得注意的是，裂纹影响Hermitian三次多项式系数值，以适应增强函数在裂纹处出现的跳跃情形。

2 Euler-Bernoulli裂纹梁的形函数和单元刚度矩阵

2.1 Euler-Bernoulli裂纹梁的形函数

不引入额外自由度，根据图1所示的计算模型，边界条件可以写为

x=0,uh(0)=ui,uh′(0)=θi

x=le,uh(le)=uj,uh′(le)=θj

(6)

假定i，j结点的位移ui，uj与转角θi，θj为已知，则由上述边界条件可以求出式(3)中的常数C1，C2，C3，C4如下

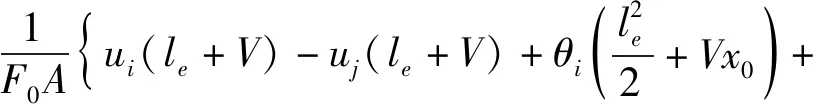
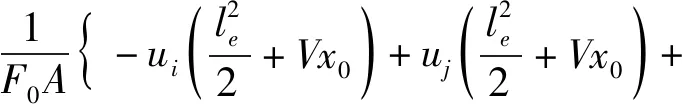
(7)

其中

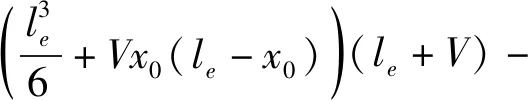
(8)

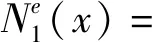
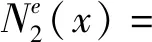
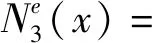
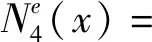
(9)

Euler-Bernoulli梁非裂纹单元的形函数如式(10)所示。

(10)

式(10)和式(9)对比知，裂纹单元形函数曲线Nie(x)(i=1,2,3,4)是三次多项式曲线fi(x3,x2,x)与函数ψi(x)的叠加。fi(x3,x2,x)与Ni(x)具有相同的函数阶次，但函数fi(x3,x2,x)的系数与裂纹位置x0和表征裂纹深度影响的参数V有关，其主要原因是适应函数ψi(x)在裂纹处出现的跳跃情形。函数ψi(x)主要表现裂纹对形函数曲线Nie(x)的附加影响，这一特征通过线性函数V(x-x0)和阶跃函数H(x-x0)的乘积实现。

当x分别为0和le时，代入式(9)得到的计算结果和式(10)计算的结果一致，表明在单元边界上裂纹引起的位移和转角为0，式(9)的形函数并不改变式(10)的边界值，自然满足单元截面连续性，无需任何手段来解决单元交界面不连续问题。

值得注意的是，当裂纹深度a=0时，表征裂纹深度的参数V=0，式(9)和式(10)等价，式(10)只是式(9)的一个特例。即当裂纹深度a=0时，Nie(x)=Ni(x)(i=1,2,3,4;x∈[0,le])。

式(3)可进一步写为

(11)

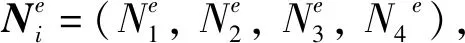
2.2 单元刚度矩阵

如图1所示的Euler-Bernuolli裂纹梁单元，假定该单元在单元结点力Vi，Mi，Vj，Mj作用下处于平衡状态。此时梁单元的挠曲线如式(11)所示，在此平衡状态下，给该单元任一虚位移δu(x)，则单元i，j结点处产生虚位移δui，δθi，δuj，δθj。根据虚位移原理有

(12)

式中，δu(x)=δδeTNeT，I为截面惯性矩，将上式写为矩阵形式如式(13)所示。

(13)

式中，Fe=(Vi，Mi，Vj，Mj)，结合式(11)～(13)得到单元刚度矩阵的计算公式如式(14)所示。

(14)

本文认为裂纹对弹性模量E和截面惯性矩I没有影响，式(14)中的抗弯刚度EI(x)为常数，再将式(9)带入式(14)就可得到裂纹单元刚度方程。值得注意的是，根据Heaviside函数的数学性质，式(14)计算过程中需要计算Dirac函数平方的积分。但Dirac函数平方的积分并没有解析解，根据Dirac函数的定义，得到Dirac函数的乘积可表示如式(15)所示。

(15)

同样，将式(15)与x2、x在单元内的积分以及式(15)自身在单元内的积分计算结果列为式(16)，并令三者的值分别为α1、α3和α2。

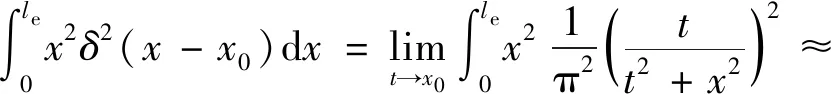
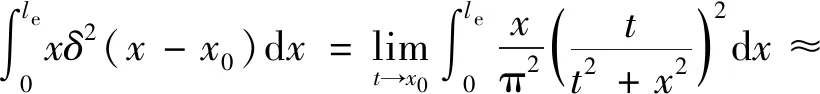
(16)

再令

(17)

最终得到裂纹梁单元各刚度项如式(18)所示。

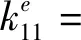
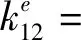
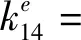
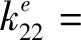
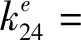
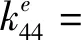
(18)

Euler-Bernoulli梁裂纹单元刚度矩阵如式(19)所示

(19)

3 裂纹参数对形函数的影响

3.1 裂纹位置的影响

假定构件长L为43 mm，构件高h为10 mm。单元长度le=L。图2给出了裂纹深度a=5 mm时，裂纹位置x0从i结点移动到j结点Nie(x)曲线变化情况。图中x/L表征归一化的位置(下同)，x0/L表示归一化的裂纹位置(下同)。

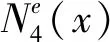
3.2 裂纹深度的影响

同等构件长度和截面高度条件下，裂纹位置x0取10 mm，图3给出了裂纹深度a从0变化到9 mm时Nie(x)曲线的变化情况，图中a/h代表归一化的裂纹深度。为方便查看Nie(x)曲线在不同裂纹深度a下的幅值变化范围，在图3中一并给出了其在平面xoNie上的投影情况。

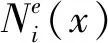
4 动静力分析验证

为说明本文修改形函数的正确性和裂纹单元刚度矩阵的有效性，分别讨论两者在实际构件静力分析和振动分析中的应用。

4.1 静力挠度分析

结构挠度是桥梁检测中常用的损伤识别指标，其主要原理是通过损伤前后结构挠度的变化对损伤进行定量和定性分析。本文将以二维纯弯简支梁和悬臂端承受集中荷载的悬臂梁为例来说明本文所提方法对结构挠度的拟合情况，简支梁和悬臂梁计算模型如图4所示，图中xc为裂纹在构件中的位置。

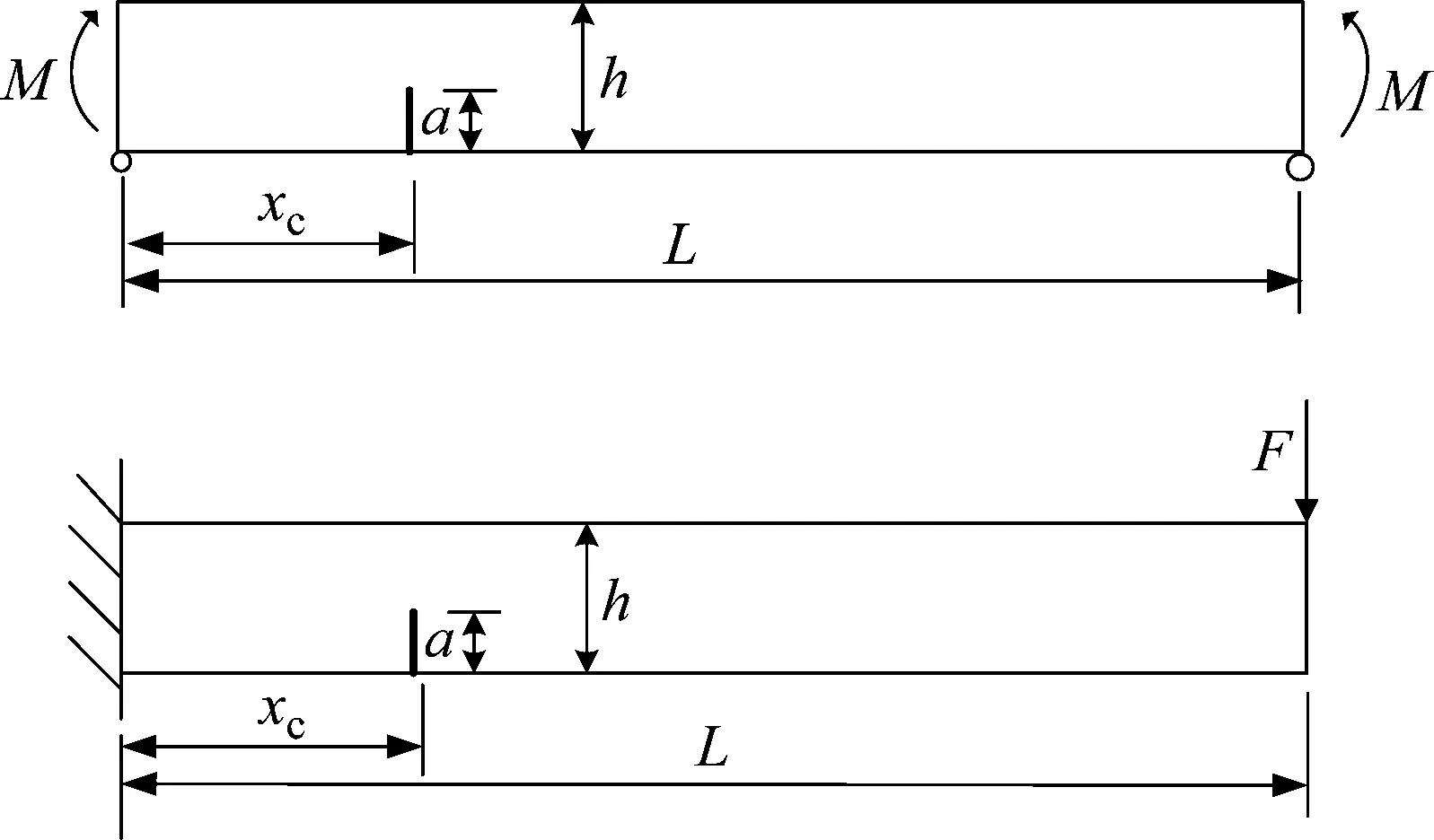
图4 二维简支裂纹梁和悬臂裂纹梁模型Fig.4 The 2-D simply supported and 2-D cantilevered beams with crack

为说明本文的有效性，同样定义挠度相对误差Re表征拟合效果的优劣。以ureal(x)表示通过有限元软件ABAQUS仿真得到的构件挠度曲线，uiden(x)表示利用式(11)的得到的构件挠度曲线，其具体表达式如下。

(20)

如图5所示，利用商业软件ABAQUS建立了Euler-Bernuolli梁的二维有限元模型，并通过数值分析方法进行了计算。简支梁和悬臂梁模型均采用CPS4R单元。其中，简支梁模型整体尺寸为0.5 mm，悬臂梁网格的横向尺寸为5 mm，竖向尺寸为1 mm。裂纹通过ABAQUS直接指派，考虑到裂纹尖端处应力场的奇异性，中间结点参数设为0.27，裂纹尖端退化单元设置为重复节点。裂纹部分的设置如图5(c)所示。

(a) 简支梁网格划分模型

4.1.1 纯弯简支梁挠度分析

如图4所示简支梁，简支长度L为43 mm，构件高度h为10 mm。弹性模量E=203.8 GPa，泊松比υ=0.3。两端施加大小为1 075 N·m的弯矩M。裂纹位置xc分别取5 mm，10 mm，15 mm，21.5 mm。裂纹深度a分别取2 mm，3.5 mm，5 mm。

整个简支梁作为一个单元，根据裂纹位置和深度由式(9)得到单元形函数Nie(x)，单元结点的转角和位移由有限元软件ABAQUS给出，根据式(11)得到本文挠度计算值uiden(x)。本文挠度计算值与有限元仿真挠度计算值比较如图6所示。

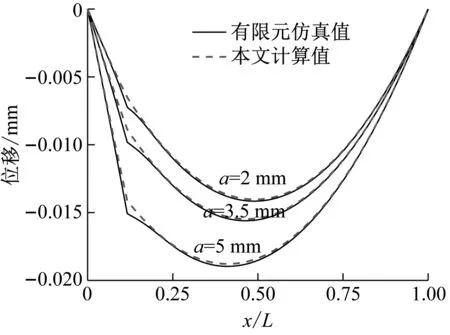
(a) xc=5 mm

图6表明不同裂缝位置处，随着裂纹深度a的增大，有限元仿真值与本文计算值整体吻合越好，裂缝附近拟合效果一般，且整体来看本文计算值在裂纹附近范围小于有限元仿真值。随着裂纹位置xc的增加，有限元仿真值与本文计算值的拟合效果的变化情况不明显。为准确描述拟合效果随裂纹位置xc的变化，将上述工况的相对误差计算结果列于表1中。

表1表明，同等裂纹深度下，越靠近支座处，有限元仿真挠度值和本文计算值的相对误差越大，越靠近跨中，有限元仿真挠度值和本文计算值的相对误差越小。当xc=5 mm时，相对误差分别为1.443%，1.714%以及1.496%。而当裂纹位于跨中(xc=21.5 mm)时，相对误差分别为0.862%，0.973%和0.731%。但表1相对误差最大值为1.714%，可以认为本文值与仿真值吻合很好。

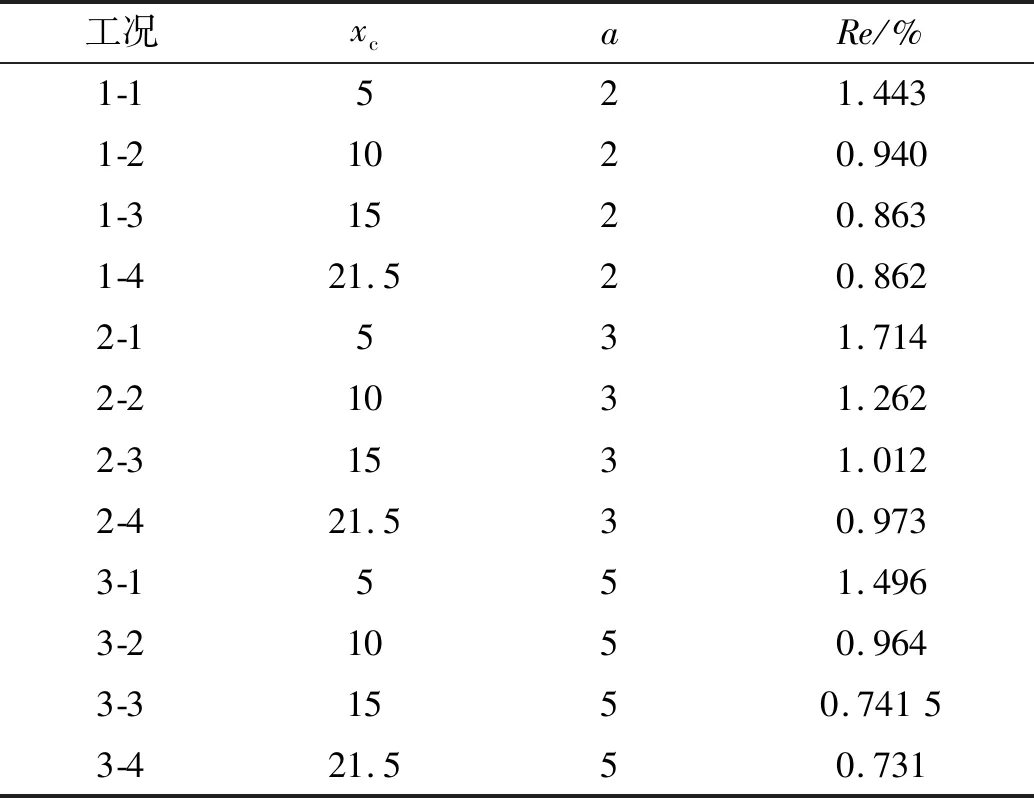
表1 各工况条件下简支梁的挠度相对误差计算Tab.1 RE of simply supported beam with different conditions

4.1.2 悬臂梁挠度分析

如图4所示悬臂梁，该悬臂梁高h为20 mm。长L为300 mm，弹性模量E=203.8 GPa，泊松比v=0.3，裂缝距固定端距离xc分别为30 mm，80 mm，100 mm，150 mm，裂缝深度a分别为4 mm，7 mm，10 mm，在自由端承受大小为100 N的集中力，方向竖直向下。

整个悬臂梁作为一个单元，根据裂纹位置和深度由式(9)得到单元形函数Nie(x)，单元结点的转角和位移由有限元软件ABAQUS给出，根据式(11)得到本文挠度计算值uiden(x)，将本文挠度计算值与有限元仿真挠度计算值比较如图7所示。

(a) xc=30 mm

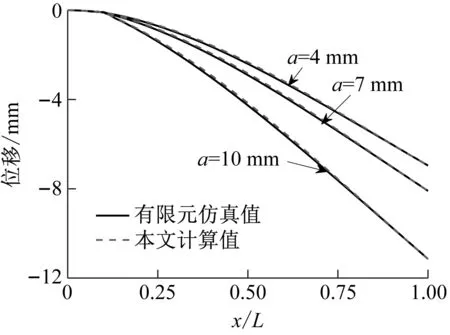
由图7知，随着裂纹向悬臂端移动，裂纹对悬臂梁挠度的影响越小。整体来看，有限元仿真值与本文计算值整体吻合很好。同样，将不同工况下的挠度值代入式(20)中量化，计算结果列于表2中。

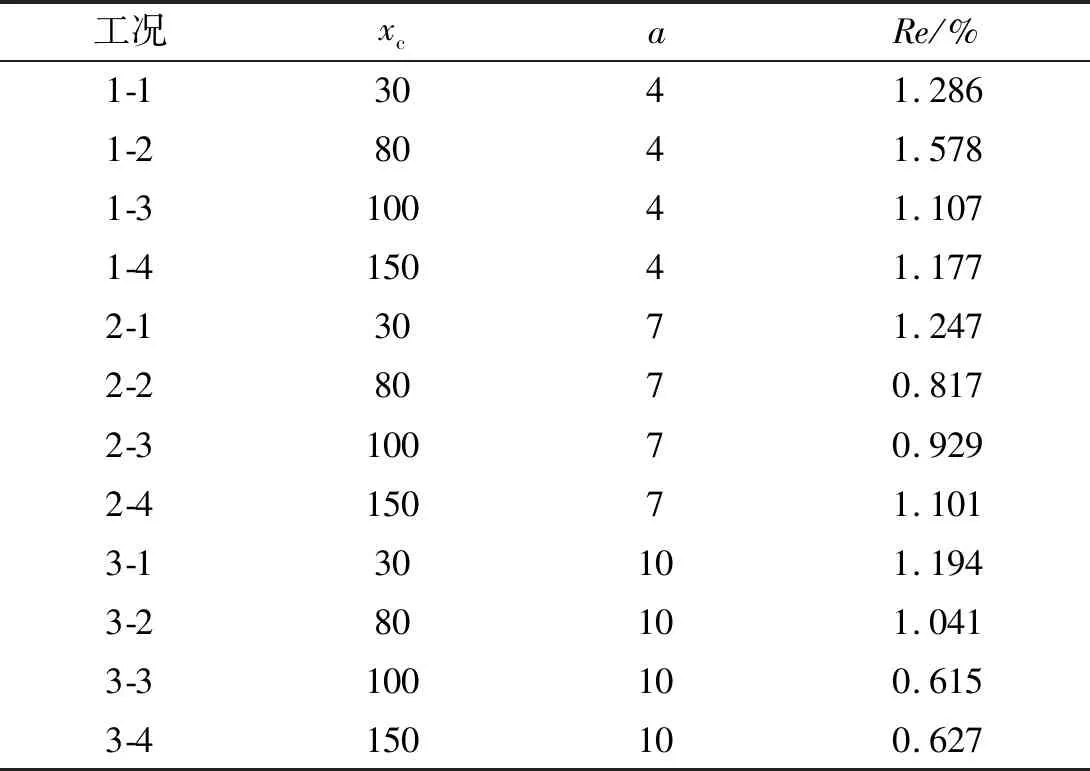
表2 各工况条件下悬臂梁的相对误差计算Tab.2 RE of cantilever beam with different conditions

整体来看，裂纹越深，本文方法拟合效果越好。越靠近支座处，拟合效果越差。与简支梁不同的是，裂纹深度a为4 mm时，悬臂梁挠度曲线在裂纹处不再出现突变的情况，而是随着裂纹位置的不同呈现出形状相似、各点位移值差距小的特征。

a=4 mm(a/h=0.2)条件下，不同裂纹位置xc时，悬臂梁自由端位移最大差值为0.496 mm，而a=10 mm(a/h=0.5)条件下，其值为3.666 mm。这表明浅裂纹(a/h≤0.2)条件下，基于静力挠度的损伤识别很难对结构损伤进行定位和分析，基于测点挠度变化分析的传统损伤识别方法更适合裂纹深度更大的工程实际。

4.2 裂纹梁振动分析

为了验证单元刚度矩阵的有效性，需要对Euler-Bernoulli梁单元振动分析。假定裂纹不引起质量矩阵的变化，截面为等截面时，沿梁长方向梁线密度ρA为常量，单元长度为le，Euler-Bernoulli梁单元的质量矩阵为：

(21)

根据裂纹几何参数，由式(19)和式(21)分别求得单元刚度矩阵和单元质量矩阵，将所有单元的单元刚度矩阵和质量矩阵分别进行叠加，以形成总体刚度矩阵K和质量矩阵M，结构的固有频率可以通过下式求得

|K-ω2M|=0

(22)

式中，ω为结构的圆频率，由圆频率ω可得结构的自振频率f如下

f=ω/2π

(23)

构件选取Sinha等用于试验的悬臂铝制梁，弹性模量E为69.79 GN/m2，质量密度ρ为2 600 kg/m3，泊松比v为0.33，梁长L为1 m，宽b为0.05 m，高h为0.025 m。根据试验过程，将悬臂边界条件转化为竖向弹簧和旋转弹簧，其中竖向支撑刚度kt为26.6 MN/m，转动刚度kθ为150 kNm/rad，计算模型如下图所示。

图8中不带圈的数字代表结点号，带圈数字代表单元号。计算工况根据Sinha等的工况选取以方便比较计算结果。同样，悬臂梁分为16个单元，共34个自由度，得到不同裂缝深度条件下的铝制悬臂梁的固有频率如表3所示(表中试验值来自文献[23])。

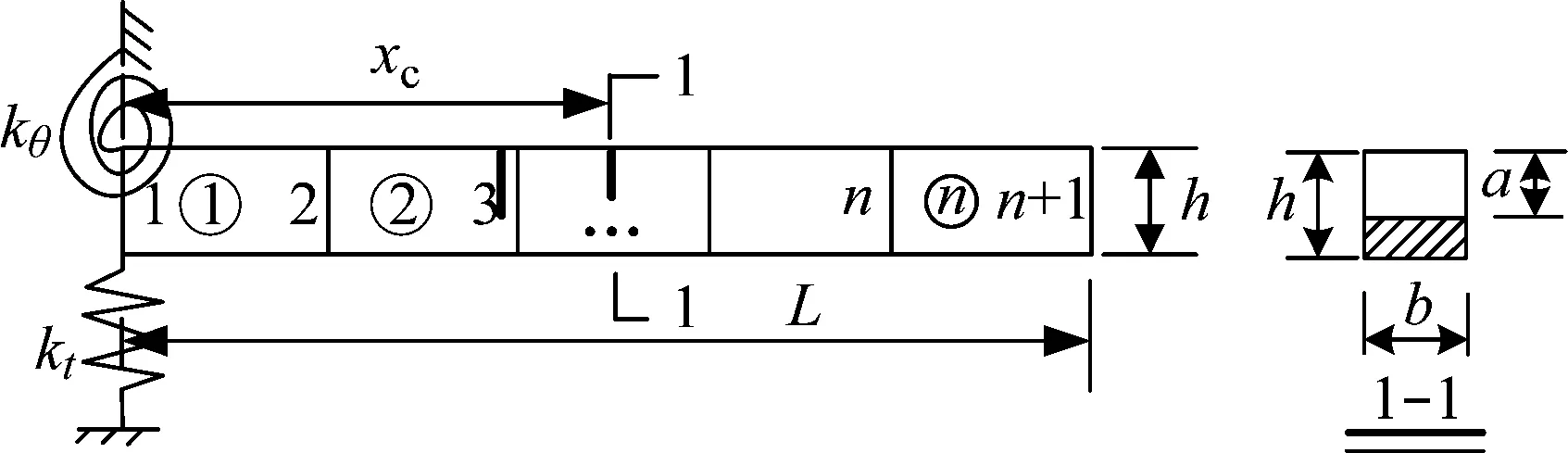
图8 悬臂裂纹梁有限元计算模型Fig.8 The FE model for the cantilever cracked beam

表3 不同裂纹深度下悬臂梁的固有振动频率Tab.3 The natural frequencies of the cantilever beam with different depth

表4可知，a/h<0.4时，本文计算值和Sinha等的计算值小于结构的实际频率；而a/h=0.48时，本文计算值和Sinha等的计算值大于结构的实际频率；a/h<0.32时，本文求解一阶固有频率的误差小于Sinha等利用抗弯刚度EI(x)折减得到一阶固有频率的误差。当裂纹深度为a/h=0.48时，本文求解一阶固有频率的误差为0.936%，大于Sinha等的计算结果0.863%，但本文一阶固有频率值的变化接近试验测得的一阶固有频率值的变化。因此可以认为本文求解结构固有频率在a/h<0.5时计算结果准确，计算结果较文献[23]的方法更好。

表4 悬臂梁的第一阶固有频率两种求解方法对比Tab.4 Comparison of two methods for solving 1st natural frequency of cantilever beam

下面具体讨论裂纹位置和深度对裂纹构件固有频率的基本影响以分析悬臂梁的自由振动特性和刚度矩阵的正确性，以fc表示裂纹构件的固有频率，fib表示完整构件的固有频率，设置参数fr表征裂缝位置和深度对构件频率的影响，表达如下。

fr=1-fc/fib

(24)

图9给出了上述悬臂构件的前三阶固有频率随着裂纹位置、深度的变化情况。

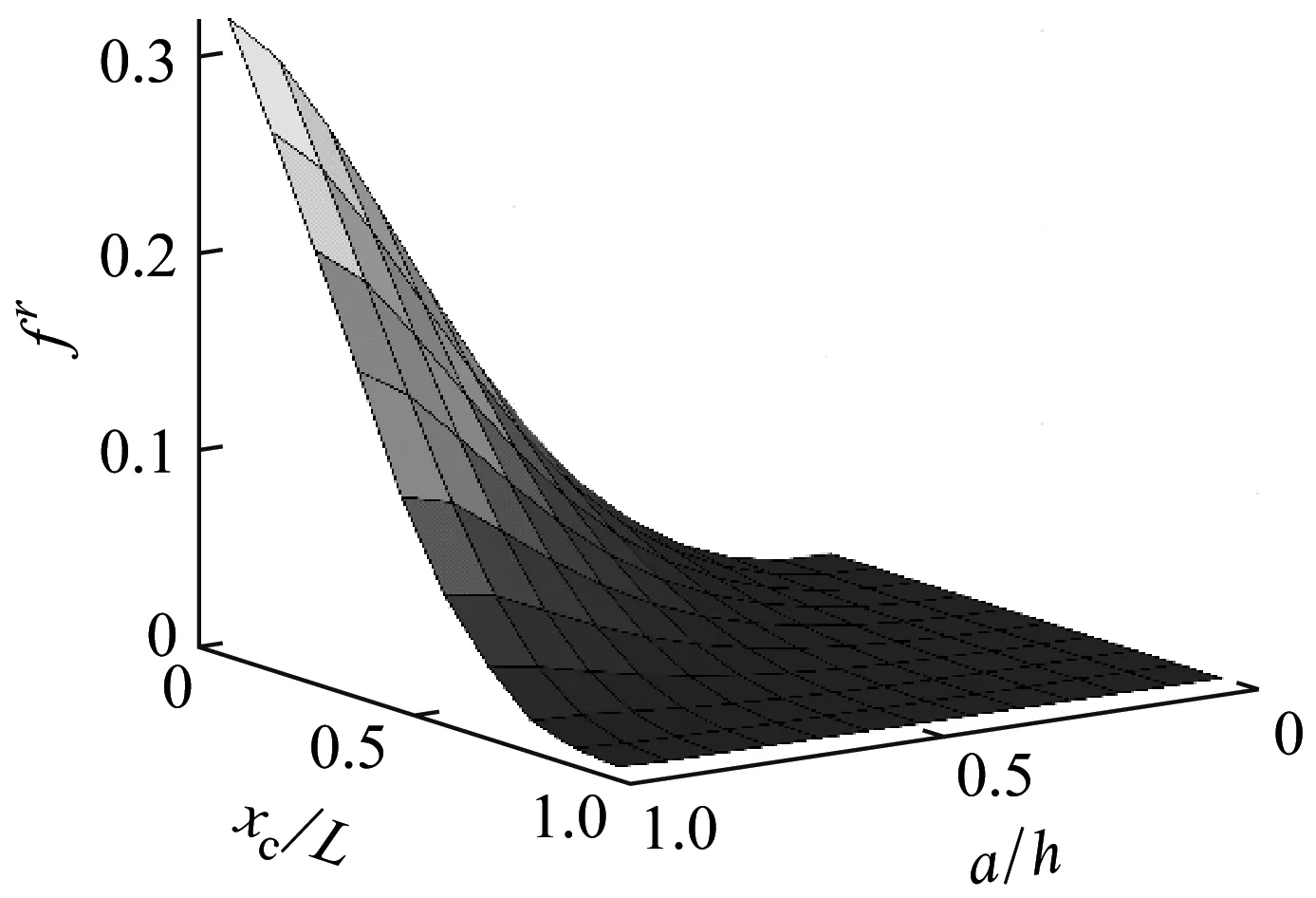
(a) 悬臂裂纹梁的一阶固有频率变化率

图9表明在裂纹位置相同条件下裂纹越深，其fr值越大，固有频率降低越明显。结构一阶固有频率呈现单调变化，裂纹距离固定端越近，裂纹越深fr值越大，反之越小。而结构二阶、三阶固有频率的fr值并不随着裂纹位置的改变呈单调性变化，二阶固有频率fr值出现两处局部最大值，三阶固有频率fr值出现三处局部最大值。上述计算结果与已有文献[35]中对悬臂构件前三阶段的振动分析结论保持一致，证明了本文裂纹单元刚度矩阵的正确性和有效性。

5 结 论

本文根据单位分解有限元思想，把增强函数附加在单元结点上，在不增加自由度的基础的给出了Euler-Bernoulli裂纹梁单元形函数和刚度矩阵的具体形式，并进行了静力分析验证和振动分析验证，主要结论如下：

(1) 该形函数能直观表现裂纹位置和深度的影响。裂纹在该形函数中表现为裂纹处幅值的突变，裂纹位置、深度与该形函数呈非线性关系。且该形函数自动满足单元协调条件，当裂纹深度为0时，该形函数退化为传统形函数。

(2) 通过简支开口裂纹梁和悬臂开口裂纹梁数值仿真，该形函数能准确拟合单元位移场。对于裂纹构件，裂纹深度越大，裂纹位置越远离结点，拟合效果就越好。

(3) 通过悬臂开口裂纹梁自由振动分析，本文所提的刚度矩阵模型能准确的描述开口裂纹对结构频率的影响。