基于复解析带通滤波器的ZFFT 算法分析与仿真

张雅希，张 琴，林 梅

（江西工业工程职业技术学院，江西 萍乡 337000）

0 引言

本文针对实时频谱分析中的关键算法进行分析研究。通常情况下，使用快速傅里叶变换（Fast Fourier Transform，FFT）算法，需在全频带内进行计算，得到的是整个采样频率上的全景频谱。而在实际的工程应用中，常常只关心某一频带范围内的局部频谱，此时若仍使用FFT 算法，进行的选定频带范围外的计算变得多余。也就是说，FFT 算法在进行局部频谱分析时存在运算量大、速度慢的缺点。目前，比较合理有效的解决方法是利用频谱细化算法对选定的频带范围进行细化频谱分析，在保证FFT 运算量不变的前提下，提高信号的频率分辨率。

常见的频谱细化算法包括线性调频Z 变换CZT 算法和基于复解析带通滤波器的ZFFT 算法［1］。考虑到CZT 算法对于谱线之间干涉较严重时的细化效果有限，本文选择对复解析ZFFT 频谱细化算法进行研究，并通过MATLAB 平台对FFT 算法和复解析ZFFT 算法进行仿真，验证频谱细化算法的有效性。

1 复解析ZFFT 频谱细化算法的原理及特点

复解析ZFFT 算法的原理如图1 所示。在对信号进行频谱细化时，首先通过复解析带通滤波器滤除无关的频率成分，而后重采样，对抽取的信号进行移频和FFT 变换处理，最终得到的频谱即为细化频谱。

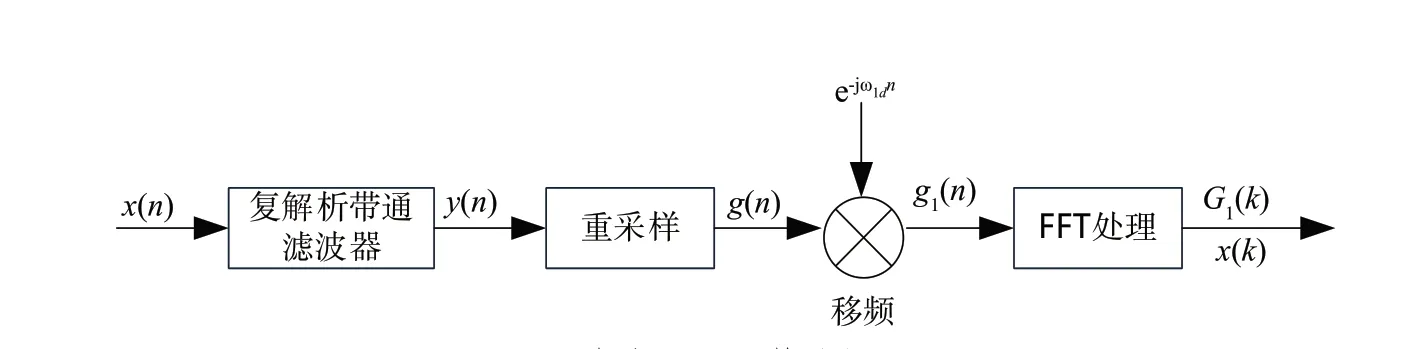
图1 解析ZFFT 算法原理图

设x(n)为待细化的数字信号序列，信号采样频率为fs，细化频带区间为f1～f2，细化频带的中心频率为，滤波器的半阶数为M且M＜＜ND，细化倍数设为D，FFT 分析点数为N，信号长度为ND+2M。算法具体原理流程如下。

1.1 带通滤波

复解析带通滤波器的带宽设为fs/2D。为了保证细化频带外的成分被完全滤除，滤波器的带宽fs/2D应等于细化带宽f2-f1［2］。为平滑滤波器的过渡带，添加汉宁窗，一般选取半阶数M=4D［3］。

对信号x(n)进行复解析带通滤波后得到信号y(n)为

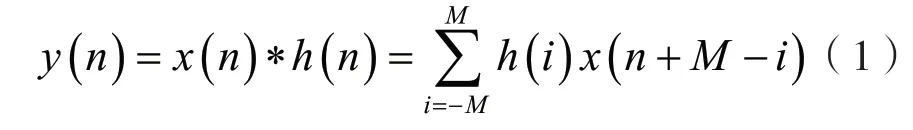
式中：h(n)为带通滤波器的冲激响应，n=0,1,…,ND-1。滤波之后，细化频带f1-f2的频谱被保留［2］，其余无关频带的频谱被完全滤除。

1.2 重采样

对y(n)重采样，每隔D点抽取出一点，信号采样频率由原来的fs降低为，信号的长度由ND降为N。重采样后的信号g(n)为

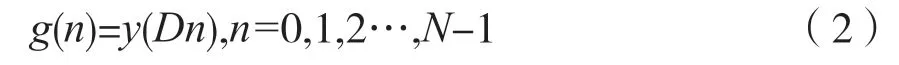
1.3 移频

对重采样后的信号g(n)进行移频，将f1移至零频点。设移频量为ω1d：

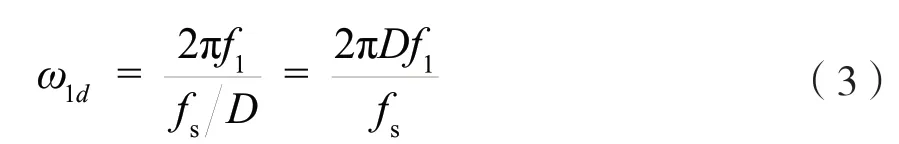
(2) 若控制有眼/无眼性状的基因位于常染色体上，请用上表中杂交子代果蝇为材料，设计一个杂交实验来确定无眼性状的显隐性(要求： 写出杂交组合和预期结果)。

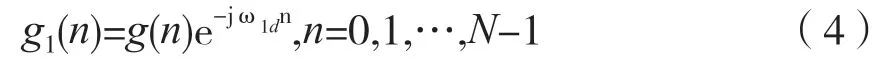
1.4 FFT 谱分析

对移频后的N点复序列g1(n)进行FFT 处理，得到相应的频谱G1(k)，G1(k)和X(k)的关系为

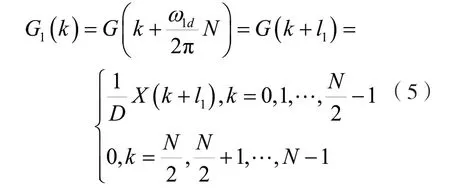
式中：l1为带通滤波时f1在Y(k)中对应谱线的位置，因为M＜＜ND，l1也可近似认为是f1在X(k)中的对应谱线的位置。

对G1(k)和X(k)的表达式进行变换后可得到：

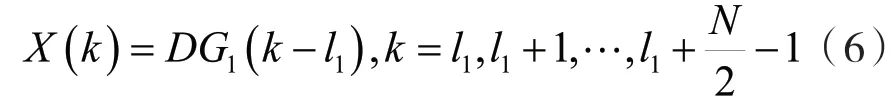
此时频谱的频率分辨率为Δf′=fs/ND，用N/2条谱线即可表示出信号选定频带的细化谱。

对于采用FFT 算法得到的频谱，其频率分辨率Δf=fs/N。如果使用FFT 算法，对长度为ND+2M的序列x(n)进行分析，对应的频率分辨率为Δf=fs/(ND+2M)；使用复解析ZFFT 算法对同样的x(n)进行分析，对应的频率分辨率为Δf′=fs/ND。因M＜＜ND，可以近似认为这两种算法分析得到的频谱频率分辨率相等，但前者需进行ND点的FFT 运算，而后者只需进行N点的FFT 运算。即复解析ZFFT 算法在保证频率分辨率的同时，减小了FFT运算量。或者说，在相同FFT 运算量的情况下，复解析ZFFT 算法的频率分辨率更高，即可实现频谱的选带细化。

2 仿真验证

通过MATLAB 平台对FFT 算法和复解析ZFFT算法进行仿真，以验证频谱细化算法的有效性。仿真测试信号涉及单频信号和密集多频信号。

2.1 单频信号的频谱仿真

用MATLAB 生成包含单个频率成分的正弦信号x1：

信号采样频率设为fs=5 120 Hz，FFT 分析点数设为2 048，则FFT 的频率分辨率为2.5 Hz。使用复解析ZFFT 算法分析时，细化频带设为60～80 Hz，细化频带中心频率70 Hz，细化倍数50，对应的频率分辨率为0.05 Hz。

在无噪声情况下和外加高斯白噪声情况下［4］（信噪比SNR=-5 dB，SNR=-10 dB）分别采用FFT算法、复解析ZFFT 算法对信号x1进行频谱分析，频谱测量结果为：在三种情况下，FFT 算法仿真估计出的信号频率均为70 Hz，误差1.15 Hz；复解析ZFFT 算法仿真估计出的结果均为68.85 Hz，误差0 Hz。图2 和图3 为在有信噪比为-10 dB 的高斯白噪声情况下，分别采用FFT 算法、复解析ZFFT算法分析得到的频谱图。观察易得，在单频信号情况下，复解析ZFFT 算法在频谱测量精度上比FFT算法更高。

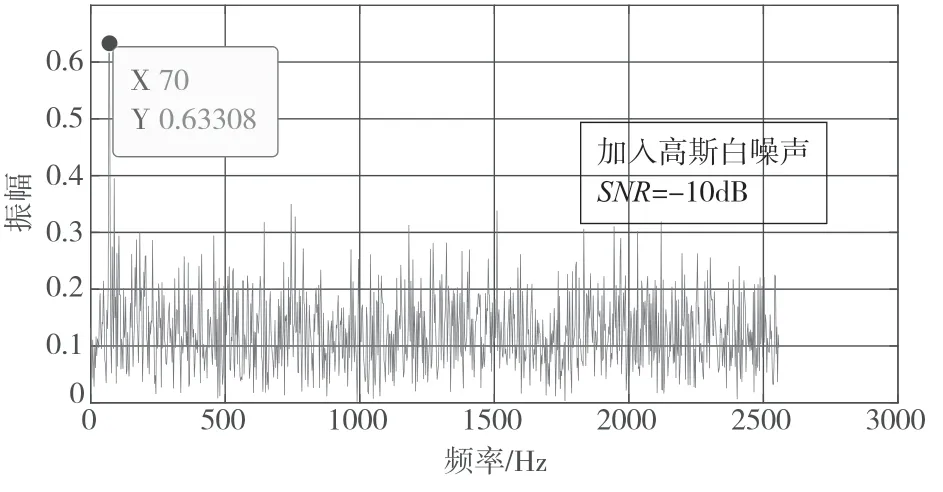
图2 FFT 频谱图（单频）

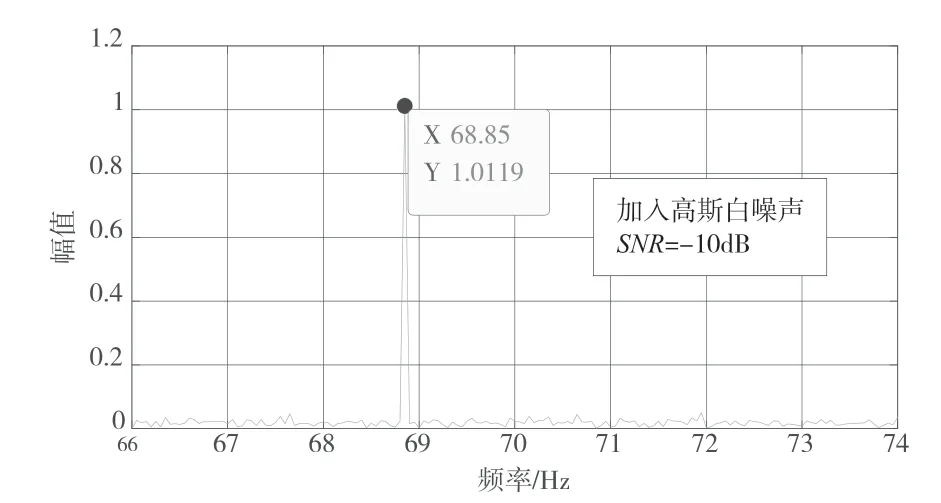
图3 复解析ZFFT 细化频谱图（单频）

2.2 密集多频信号的频谱仿真

用MATLAB 生成包含多个密集频率成分的正弦信号［5］x2：

式中：信号频率fx2=68.35 Hz，fx3=69.70 Hz，fx4=70.23 Hz，fx5=70.85 Hz，fx6=71.06 Hz，信号幅度分别为3，5，4，3.5，6。

信号采样频率设为fs=5 120 Hz，FFT 分析点数设为2 048，则FFT 的频率分辨率为2.5 Hz。使用复解析ZFFT 算法进行分析时，将细化频带设为60～80 Hz，细化频带中心频率70 Hz，细化100 倍，相应的频率分辨率为0.025 Hz。

与单频信号的仿真类似，在无噪声情况下和外加高斯白噪声（信噪比SNR=-5 dB，SNR=-10 dB）情况下分别采用FFT 算法和复解析ZFFT 算法对信号x2进行频谱分析，频谱测量结果为：在三种情况下FFT 算法仿真估计出的结果均为70 Hz，不能将5 个频率相差很近的信号区分开；对应的复解析ZFFT 算法仿真估计出的结果68.35 Hz，69.70 Hz，70.225 Hz，70.85 Hz 和71.05 Hz，误差分别为0 Hz，0 Hz，0.005 Hz，0 Hz 及0.01 Hz。图4 和图5 为在有信噪比为-10 dB 的高斯白噪声情况下，分别采用FFT 算法、复解析ZFFT 算法分析得到的频谱图。观察发现，图4 频谱图上只能看到一个谱峰，而图5 频谱图中5 条谱线清晰可见，在有噪声情况下，也能够完全区分开这5 个频率成分。

图4 FFT 频谱图（密集多频）

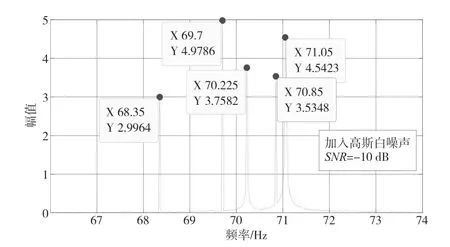
图5 复解析ZFFT 细化频谱图（密集多频）

3 结语

本文主要针对基于复解析带通滤波器的ZFFT频谱细化算法进行分析研究，同时设计合理的仿真方案，通过MATLAB 平台对传统FFT 算法和复解析ZFFT 算法进行仿真。仿真结果表明，无论是在单频信号、多频信号还是密集多频信号的情况下，使用复解析ZFFT 算法进行局部频谱分析都具有明显优势，在相同FFT 运算量的情况下，其频率分辨率远远高于FFT 算法。特别是在密集多频信号的频率估计中，复解析ZFFT 算法能够将FFT 根本无法分辨出的多个密集频率成分准确地细化出来，实现局部细化频谱。