三丝型质点振速传感器的模型分析

王绥昌，郭轩瑞，朱林辉，张 颖，郭 航*

(1.厦门大学 萨本栋微米纳米科学技术研究院，福建 厦门 361005; 2.厦门大学马来西亚分校 新能源科学与工程系,马来西亚 雪邦 43900；3.厦门大学马来西亚分校 电子信息工程系，马来西亚 雪邦 43900)

声学测量系统在环境监测、汽车工业、军事国防等领域都发挥着重要作用。要完整地描述一个声场，需要知道标量声压和矢量质点振速两个参数。1994年荷兰de Bree提出了一种采用微机电系统即MEMS技术来加工制造的质点振速传感器(Particle Velocity Sensor,PVS)[1]，它以气团运动代替质量块振动，通过测量热源对称位置的温度差变化，从而确定引起器件微通道内气体流动的声场的质点振速。在随后的十多年间，以此技术为基础的荷兰Microflown Technology 公司所开发的由声压计与PVS所构成的声学探头，即矢量传声器，在军用与民用领域都得到了广泛应用[2-3]，目前仍在深入研究当中。国内对PVS的研究起步较晚，2014年中国电子科技集团公司第三研究所对矢量传声器技术进行了研究探索，微加工制备了两丝型PVS[4]，对其性能进行了测试分析与优化；2019年北京大学微加工制备了三丝型PVS，进行了测试研究[5-6]。国内其他单位如中国计量学院[7]、厦门大学[8]等也做了深入研究。

PVS是矢量传声器的核心部件，目前主要有两种结构形式：一种是两丝型，包含两根平行排列、具有一定间距的热阻丝结构，如图1所示，这两根丝既是加热丝，又被用作传感器的敏感丝；另一种结构是三丝型，如图2所示，是包含三根平行排列具有一定间距的热阻丝结构，两边的是敏感丝，中间的是加热丝。虽然两丝型结构灵敏度比三丝型较高，但不是特别显著，并且三丝型与两丝型相比将热源和传感器隔离开来，可有效避免热噪声的影响。

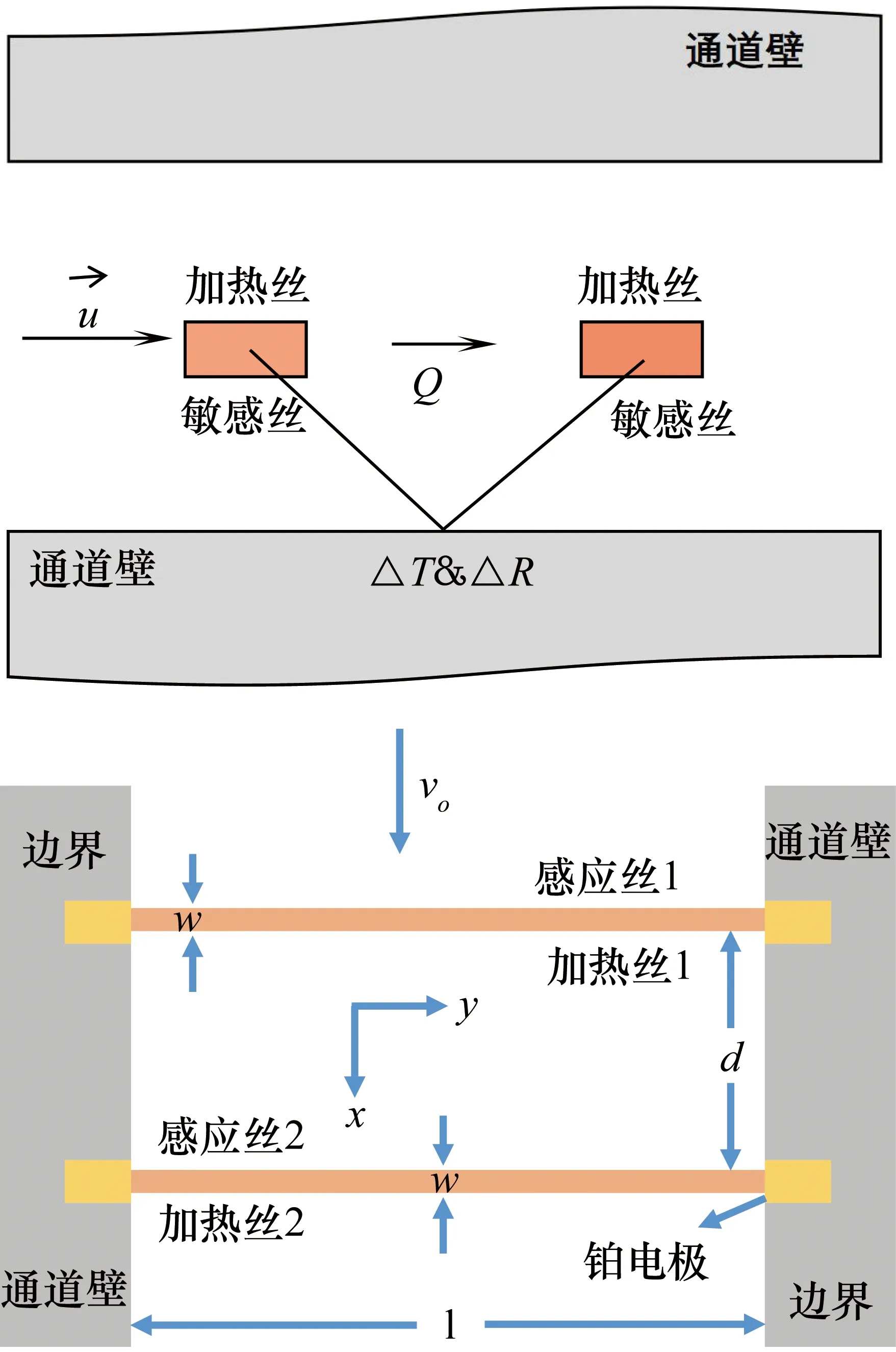
图1 两丝型PVS横截面及俯视示意图

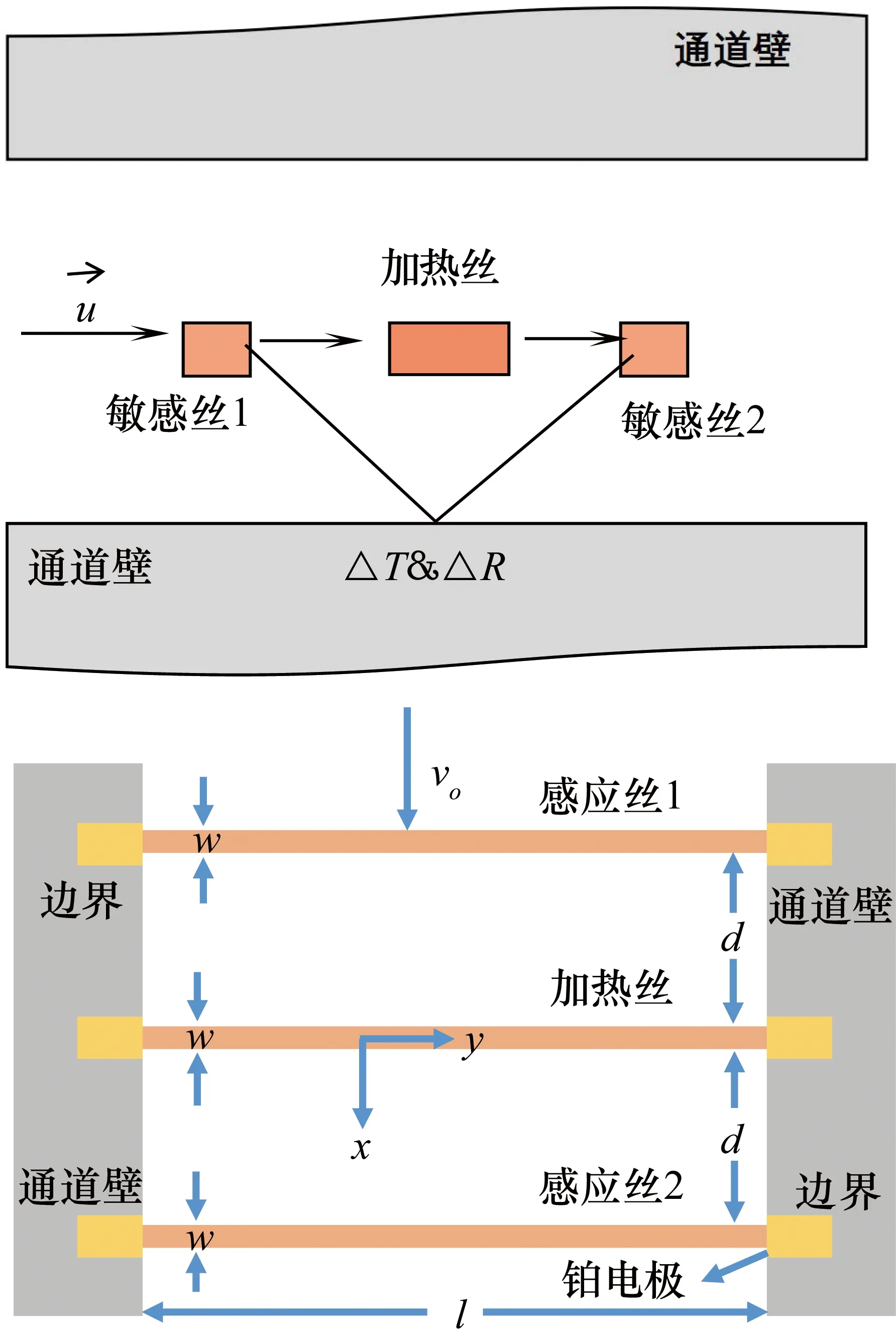
图2 三丝型PVS横截面及俯视示意图

PVS是目前唯一的一种能够直接测量空气质点振速的传感器，其灵敏度、噪声、功耗、工作频段等直接决定矢量传声器的性能。因此，其分析设计至关重要。

目前已有对两丝型PVS的分析模型的研究，对于三丝型则较少。本文对三丝型PVS的模型进行研究，从稳态与瞬态的热传导分析出发，建立起三丝型PVS的解析模型，并与数值模型进行对比验证，从而为三丝型PVS的优化设计与微加工制造提供理论基础。

1 三丝型PVS的解析分析

如图2所示，在三丝型PVS中，两根热阻丝在中间的加热丝的左右两边对称平行放置，作为敏感单元。整个传感器的腔壁为热绝缘且不可渗透的边界，使通道内部尽可能小地受外界环境影响。当没有声场且加热丝所受恒定电压不变时，微通道内部温度场处于稳态，两根敏感丝的温度差为0，即ΔT=0。当外界施加一个声场时，离声源较近一侧的粒子会产生振动[9]，从而在靠近声源一侧的微通道入口处引起通道内介质发生受迫对流运动，形成一个热扰动场，使两根敏感丝温度不相等，即ΔT≠0。设中间加热丝的长度、宽度、厚度分别为l、w、h;左右两根细丝仅作为敏感器件长度与加热丝相同，与加热丝的距离均为d。

两根敏感丝的温度差可以通过热电阻效应转变为电阻值之间的差异，经过惠斯通电桥电路分别得到两者的阻值。质点振速与敏感丝温度差的关系为

(1)

式中：Ub为施加在敏感丝上的电压值；r为敏感丝材料的温度系数；v为腔体内质点振速；ΔT(v)为敏感丝的温度差，是关于质点振速v的函数。经过相关计算与比较，后续的讨论中将微通道内总温度场拆分为稳态温度场和热扰动场的耦合。

1.1 稳态温度场模型

如前所述，温度场是由中间的加热丝产生的。通道中气体的低速运动可以近似为层流，其粒子沿平行于通道的直线平滑移动。因此，从加热丝到空气的传热模式是基于热传导方式。有热源的热方程[9]可以用来描述这种导热模式：

(2)

式中：U为腔体内各位置的温度分布；α为热扩散系数；F(x,y,z,t)为与时间相关的腔体内的热量分布函数；K为空气的导热系数；p为空气的密度；s为空气的比热；Q为腔体内每单位体积的热能。通过变量分离，可得：

U(x,y,z,t)=T(x,y,z)L(t)

(3)

式中：T(x,y,z)为与时间无关的稳态温度分布；L(t)为温度场与时间相关的变化幅度。假设温度场在距离加热丝l/2点处的衰减为0，因此，稳态热传导方程可以简化为

-k2T=Q

(4)

假设加热丝在y方向的长度为无限长(l≫w,l≫h)且在x和z方向上无限薄。然后，可以近似认为温度场沿y轴没有发生变化。因此，可以化简并省略三维解析模型中的y方向温度场的分析，只考虑温度在x和z方向的分布，从而将三维模型转化为二维模型。假设施加在加热丝的电功率为P，则单位长度的功率为P/l，那么加热线每体积产生的热量为

(5)

式中：δ(x)和δ(z)为冲激函数，表示加热丝被近似认为沿y方向没有厚度和宽度。将式(5)代入式(4)可得：

(6)

将式(6)转化为极坐标并进行积分运算，则其通解为

(7)

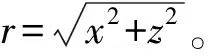
(8)

从而将三维解析模型化简为一维解析模型。然而，由于在上述分析中忽略了加热丝的宽度，当x接近零时，T(x)不能完全描述从-w/2到w/2的温度分布。可以通过将宽度视为连续点源从-w/2到w/2的连续对称分布来计算加热丝的平均温度。因此，式(8)可通过设置x=0来计算平均值：

(9)

PVS几何参数与物理常数如表1所示。将表1中参数代入式(9)可得加热丝上温度约为621.8 K，再经式(8)计算，可得三丝型PVS微通道内稳态温度场分布，如图3所示。从图3中可以看到图像左右对称，表明在没有声源情况下，两根敏感丝的温度差为0。

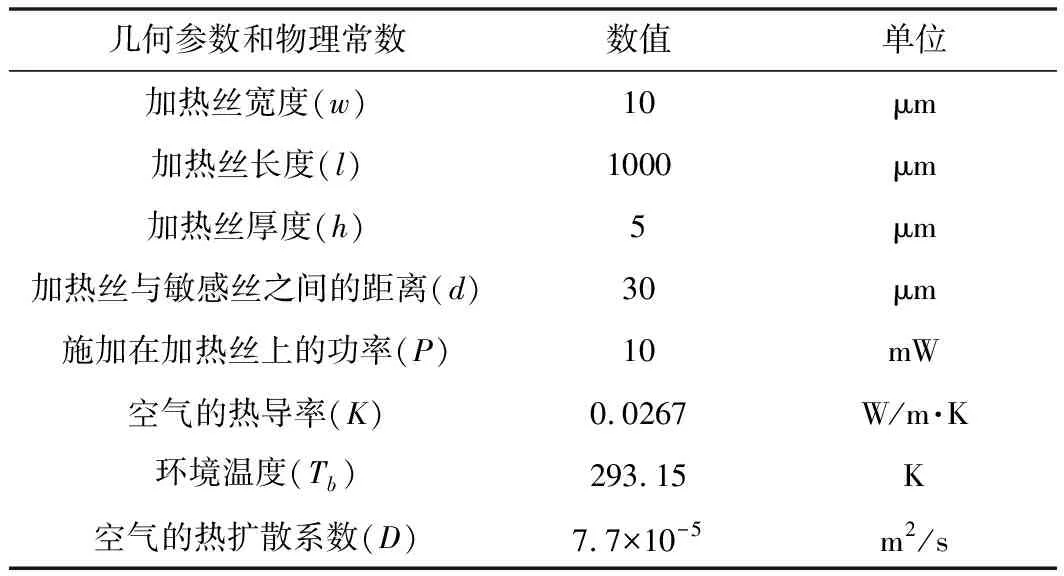
表1 PVS几何参数与物理常数

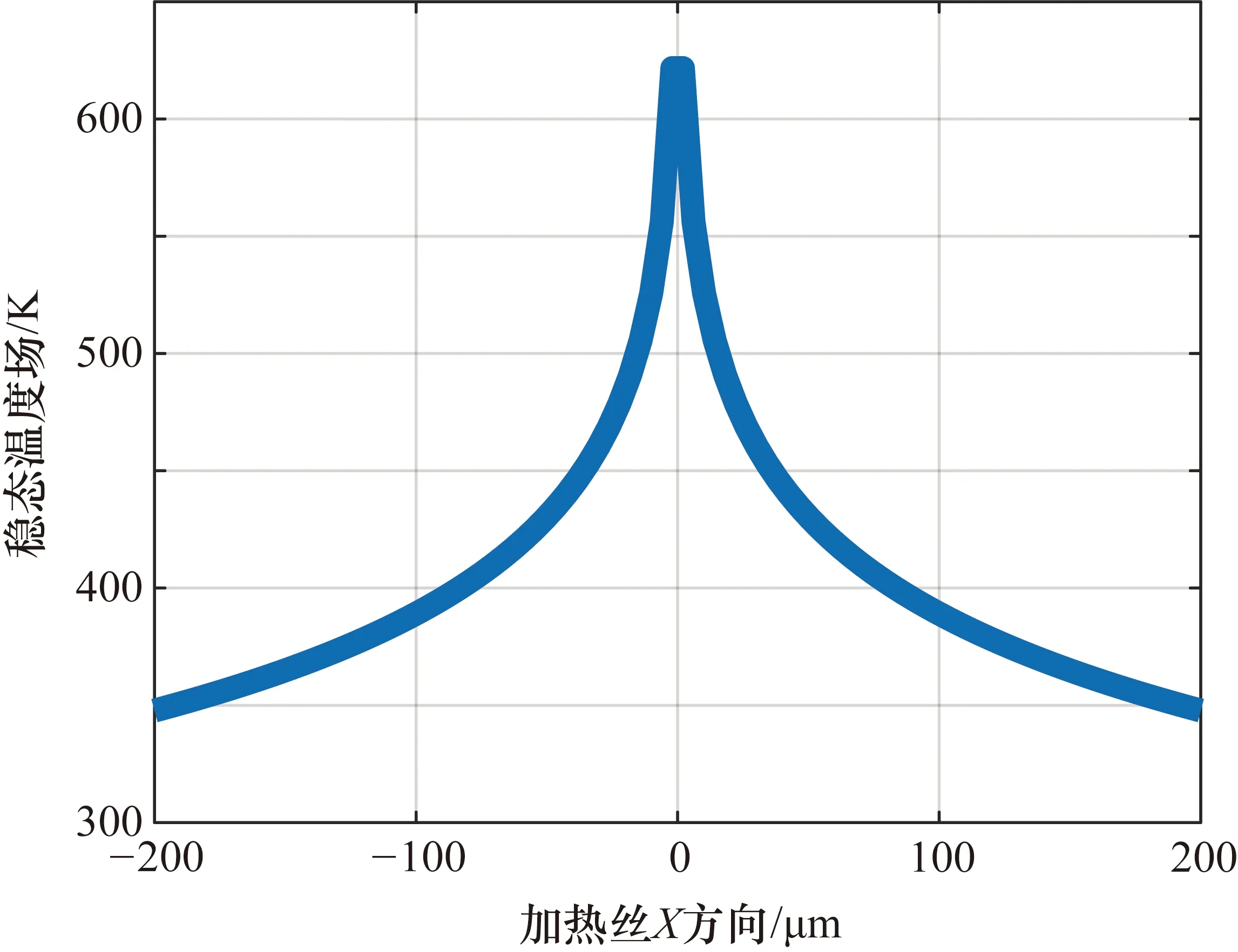
图3 PVS稳态温度场

1.2 动态温度场模型

当声波进入传感器的微通道时，靠近声源的粒子将开始振动，导致气体在通道中移动。

对于粒子的这种运动，假设总温度场是稳态温度场和热扰动场的叠加。温度可以从热方程中求出

Ps(∂tTe+vTe)-K2Te=Q

(10)

式中：Te为当声波进入微通道后的总温度场；v为质点振动的速度；vTe为由进入微通道声波所带来的强迫对流运动;Q为由式(5)定义的热功率密度。

当比较热扩散过程和强迫对流运动时，由于一个粒子从一根丝扩散到另一根丝的时间为l2/D，而强迫对流运动的时间为l/v。比较这两次运动的时间，可得

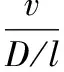
(11)

式中：热扩散系数D=k/ps≈1.9×10-5m2/s(空气)；强迫对流的速度v=4.4 mm/s(对应100 dB下的较高的声压)。由于热扩散速度D/l≈0.2 m/s远大于质点振速v。假设温度为T+δT，其中T是稳态情况下的温度分布，δT是对流引起的校正。因此，用T+δT替换Te，将公式(9)转换为

(12)

从前面的分析可知，三丝型PVS的物理模型已简化为一维解析模型，即仅为x方向的温度分布。可知，∂tT=0,vT=v∂xT,vδT=v∂xδT,-K2T=Q。根据Mailly等[10]的实验，x方向的温度分布梯度远大于扰动梯度。因此，位于x方向的项∂xδT，在方程(12)中可以忽略，从而得到：

(13)

在声学分析中，声波的振动是周期性变化的，声波引起的质点振速可定义为

v=v0ei(2πft+φ0)

(14)

式中：f为声波的频率；φ0为声波的初始相位，则温度校正可以被表示为

(15)

将式(7)、式(14)和式(15)代入式(13)，式(13)可写为

(16)

当x和z趋近于0时，式(16)无法直接求解。因此，可以通过z坐标上对该式进行傅里叶变换来求解

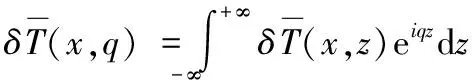
(17)

式中：q是沿z方向的温度梯度，通过将式(17)代入式(16)，表达式可以转换为

(18)

(19)

式中：q应解释为绝对值|q|。此时，式(18)的解在x=0时是连续的，并一直衰减，其表达式为

(20)

通过对式(20)进行傅里叶逆变换并用贝塞尔函数求解，可以得到简化的热扰动场

(21)

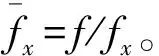
当声场振动频率为 300 Hz、声压级为 94 dB、质点振速为v0=2 mm/s时，在式(21)中代入表1中数据，可得到沿微通道中心方向上的热扰动场分布，如图4所示，声波从微通道一侧(x负方向)进入腔体内，引起的热扰动场在靠近通道入口处腔体一侧为负，靠近出口一侧为正，从而使两根敏感丝温度值不相等。

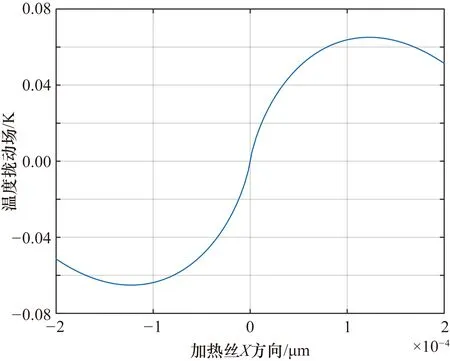
图4 PVS热扰动场

总温度场是稳态温度场和热扰动场的叠加，可以表示为

(22)

上述方程为三丝型PVS的基本解析模型，传感器墙体内稳态温度场于声波传来时的总温度场分别如图5蓝色实线与红色虚线所示，证明了当声波引起空气中质点发生振动使静态温度场与热扰动场耦合时，使两根敏感丝温度不再相等，产生温度差。

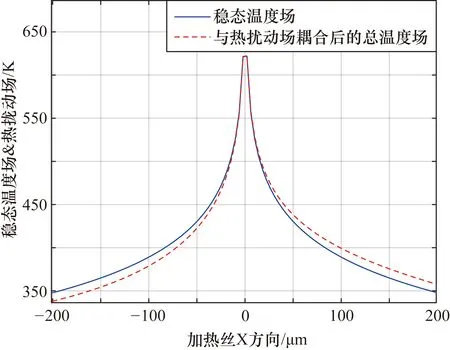
图5 PVS总温度场

2 三丝型PVS的有限元分析

为了验证上述解析模型的准确性和探讨解析模型与实际器件性能上的差别，本文采用数值模拟的方法对矩形通道内单热源自然对流和强制对流进行了仿真以贴近实际传感器腔内换热情况。该模型采用有限元的方法(Finite Element Method,FEM)[11]将PVS的腔体、流体介质和热阻丝等沿坐标轴方向划分为有限数量控制单元。本文利用有限元分析软件ANSYS中的Fluent模块对上述问题进行求解。

传感器简化三维模型的微通道如图6所示，其长、宽、高分别为0.6 mm、0.6 mm、0.3 mm，两根敏感丝与中间加热丝的距离均为0.08 mm。当声波引起微通道入口处质点发生振动后，会使腔体内部空气发生受迫对流运动，并在出口处流出。之后，对该模型进行网格划分如图7所示，在三根热阻丝附近采用了更高精度的网格划分以提高仿真的精度，本次共选用15303个网格，兼具了简洁与准确性。

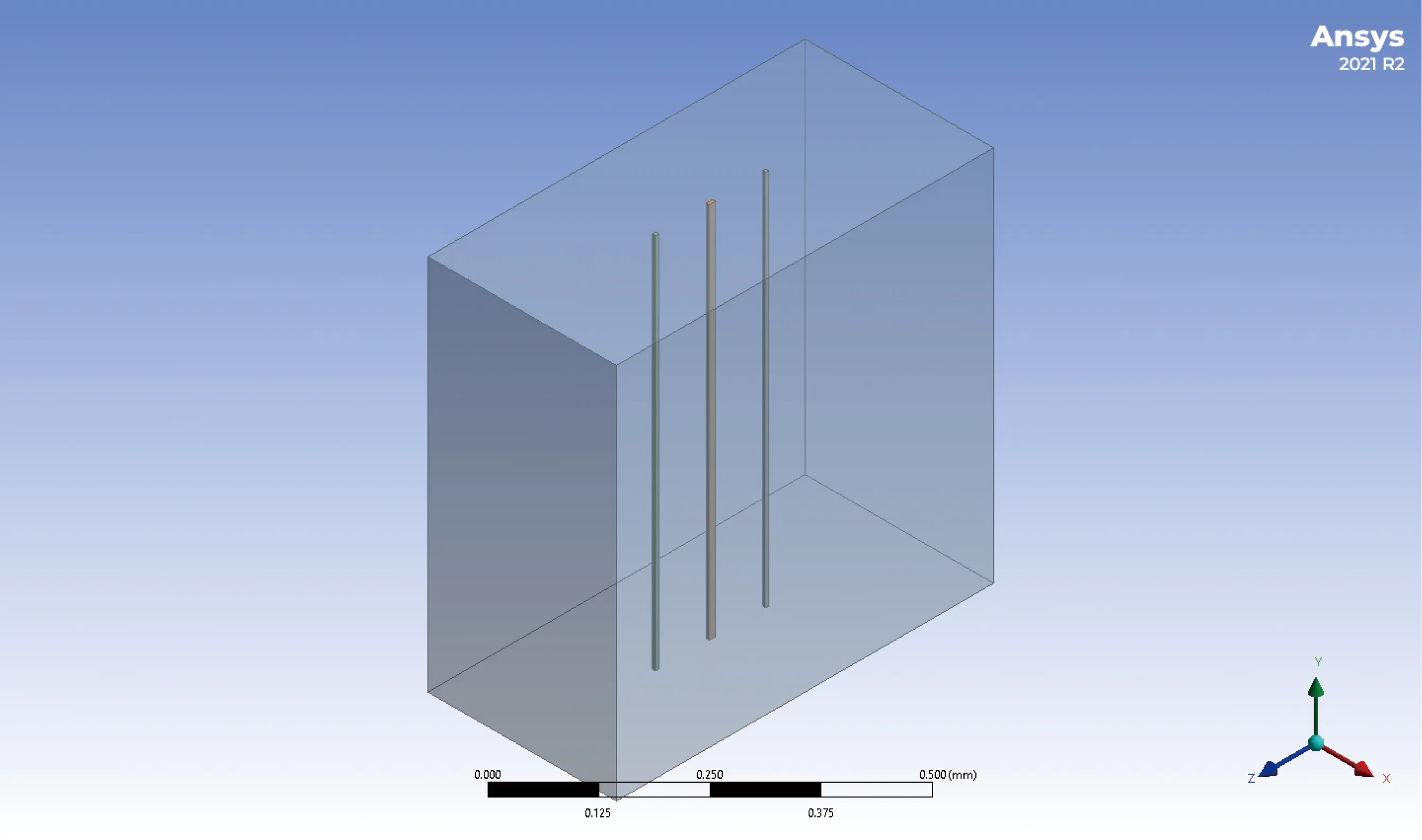
图6 PVS数值仿真模型

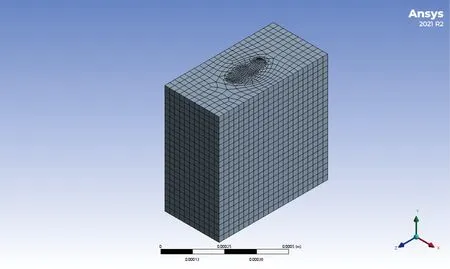
图7 PVS数值仿真网格节点

加热丝和感应丝以铂为材料且密度和比热为21450 kg/m3和130 J/kg·K。对于密度和比热，空气在流体域的边界条件分别为1.225 kg/m3和1006.43 J/kg·K。以上述条件为基础，ANSYS Fluent进行了如图8所示的稳态温度场仿真。其结果表明在没有热扰动的情况下，加热丝产生的热量均匀且逐渐地分布到两侧，使两敏感丝具有相同的温度。

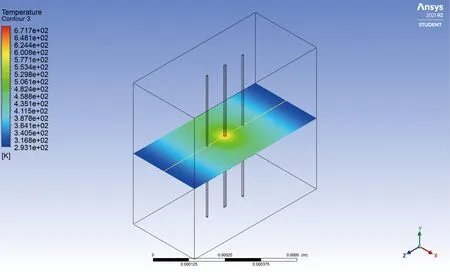
图8 PVS数值仿真稳态温度场

为了验证这两个部分的准确性以及可靠性，数值仿真与解析模型进行对比验证如图9所示。在稳态温度场中，数值仿真与解析模型中间丝的最高温度分别为621.0 K和621.8 K，这显示了解析模型体现了与理论值极相似的最高温度值，两者间只有0.13%的误差。在有温度扰动的情况下，入口速度为 2 mm/s时，以模拟缓慢稳定的流动，数值仿真与解析模型有少许变动如图 10 所示，两感应丝之间会有温度偏差。模型与理论值，中间丝的最高温度分别为620.2 K和621.4 K。与稳态温度场相比，中间丝的最高温度，在数值仿真与解析模型中分别减少了0.8 K和0.4 K。数值仿真与解析模型具有相似的温度趋势，只是当中解析模型的整体温度比数值仿真的整体温度较低。

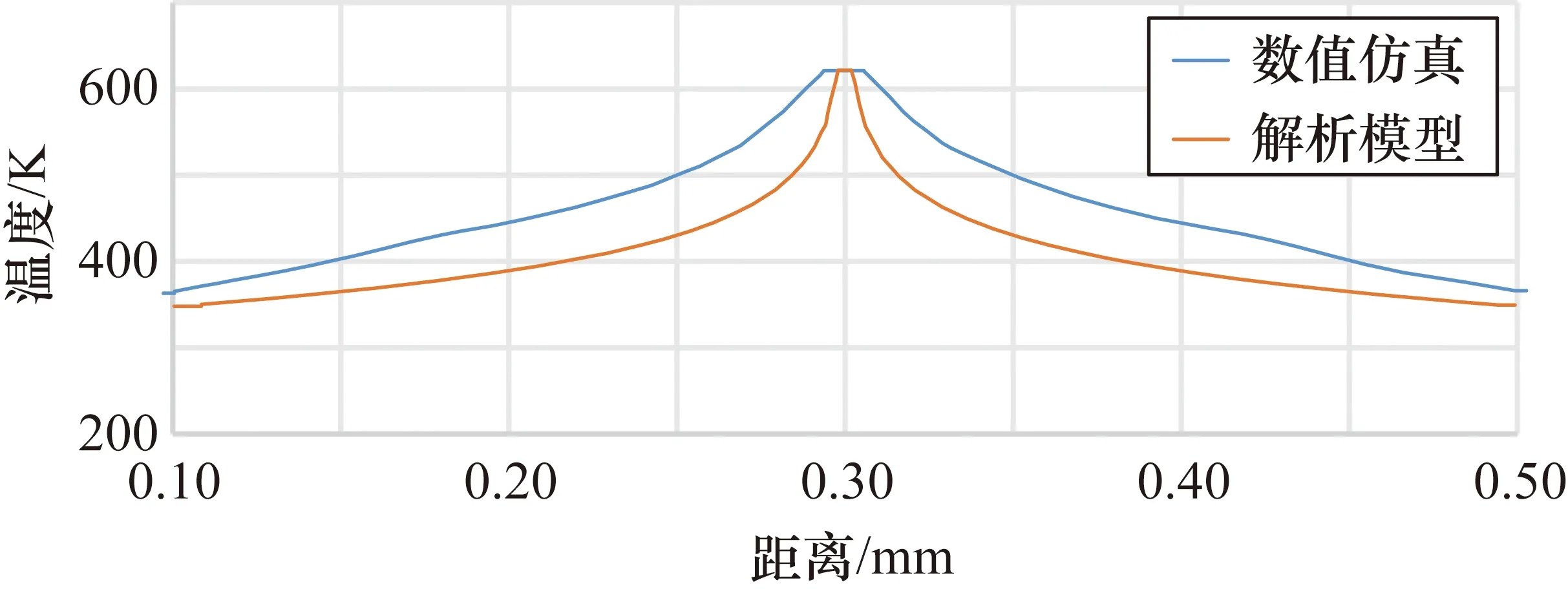
图9 稳态温度场PVS数值仿真与解析模型验证

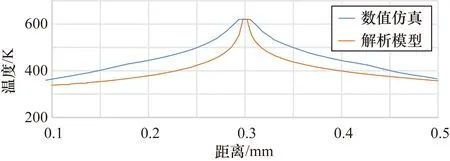
图10 热扰动场PVS数值仿真与解析模型验证

3 结束语

本文从热传导方程出发，初步建立了三丝型PVS的稳态温度场模型和热扰动场模型，利用ANSYS 软件建立三维模型，对三丝型PVS进行了热传导与层流运动耦合的数值仿真，并验证解析模型的准确性，结果表明数值模拟和解析模型均具有很好的可靠性。