基于FADS/IMU信息融合的大气数据测量方法研究
肖地波,蒋保睿,刘 鹏
(成都信息工程大学 自动化学院,四川 成都 610225)
对于飞行器而言,传统的空速管、攻角传感器等大气数据测量装置在高速、高机动性的飞行时会产生较强干扰,且对飞行器的隐身效果有一定的影响。嵌入式大气数据传感(Flush Air Data Sensing,FADS)系统依靠机体表面的压力分布,通过一系列算法间接获得动静压、攻角、侧滑角等大气数据,具有维护成本低、经济性良好等特点,被广泛用于航空航天领域[1]。
目前,美国[2]与欧洲[3]对FADS系统开展了大量研究,并已开发出成熟产品。国内学者王鹏[4]研究了用于尖楔前体飞行器的FADS系统算法,并且对算法进行了验证和测试。王禹等[5]提出了适合工程应用的飞翼布局飞机的FADS 算法模型。
然而,由于气压传感器的测量噪声和延迟等问题,导致其单独使用时对数据的估计精度有限[6],而惯性测量元件(Inertial Measurement Unit,IMU)的数据的瞬时精度较高、延迟较低,可以用于FADS的辅助计算。以IMU测量的加速度、角速度作为飞行器模型的输入量,以FADS获得的角度和速度信息作为观测量构建卡尔曼滤波是一个常用的方法[7]。因为飞行器飞行时涉及到坐标系转换和当地声速变化的计算,所以需要对原有的卡尔曼滤波进行改进,以满足非线性系统的计算要求。陆辰等[8]提出了一种基于 FADS 的扩展卡尔曼滤波(Extended Kalman Filtering,EKF)实时估计大气参数的方法,验证了惯性数据测量大气数据的可靠性,同时建立了大气数据传感信息融合测试平台,能提高大气数据系统的精度和稳定性。程超[9]采用卡尔曼滤波理论,设计了捷联惯性导航系统/大气数据系统组合导航滤波算法,并对算法的有效性进行了仿真验证,证明了惯性导航系统和大气数据系统两者进行融合是有效的。Nourmohammadi等[10]将容积卡尔曼滤波(Cubature Kalman Filter,CKF)用于惯性导航系统和卫星导航系统的信息融合上,获得了比EKF更高的导航精度。
针对高马赫数飞行器的大气数据测量与估计的方法进行研究,提出了基于CKF的FADS/IMU耦合的大气测量方法,利用大气与飞行器飞行数据建立滤波算法模型,对飞行器的马赫数、攻角、侧滑角等重要大气数据进行高精度估计,并完成大气数据测量仿真分析。
1 系统设计
1.1 算法流程概述
基于CKF的FADS/IMU数据融合大气数据估计系统包括直接测量大气数据的FADS解算、IMU数据解算和CKF信息融合估计。算法流程如图 1所示。
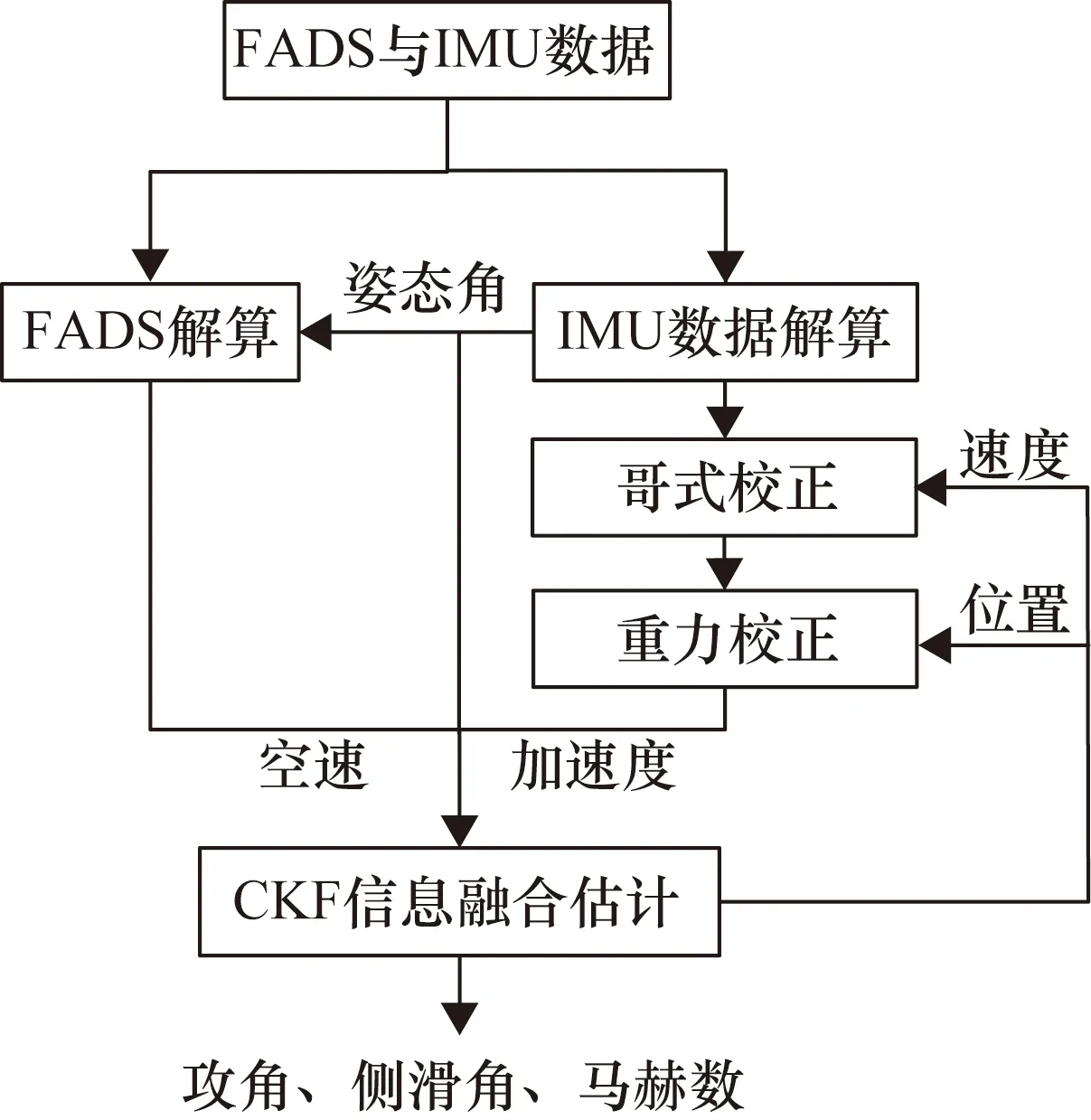
图1 算法流程图
CKF是贝叶斯滤波中的一种可广泛应用于非线性滤波问题的滤波器,相比于UKF算法,CKF避免了因矩阵分解可能会出现的矩阵奇异问题,而且对于高维非线性系统,其状态估计精度更高。文献[11]经过分析对比得出:当系统状态维数大于3时,CKF算法的估计精度高于UKF算法。
1.2 FADS与IMU数据预处理
研究的FADS算法通过飞行器表面特定区域的压力分布反推得到飞行参数,解算顺序一般为:动静压、攻角侧滑角、马赫数和气压高度。构建以5个测压点为输入的FADS系统,其中一个点位于机头中心,其余4个点均匀分布在四周,以球形机头为例,开孔位置示意图如图2所示。
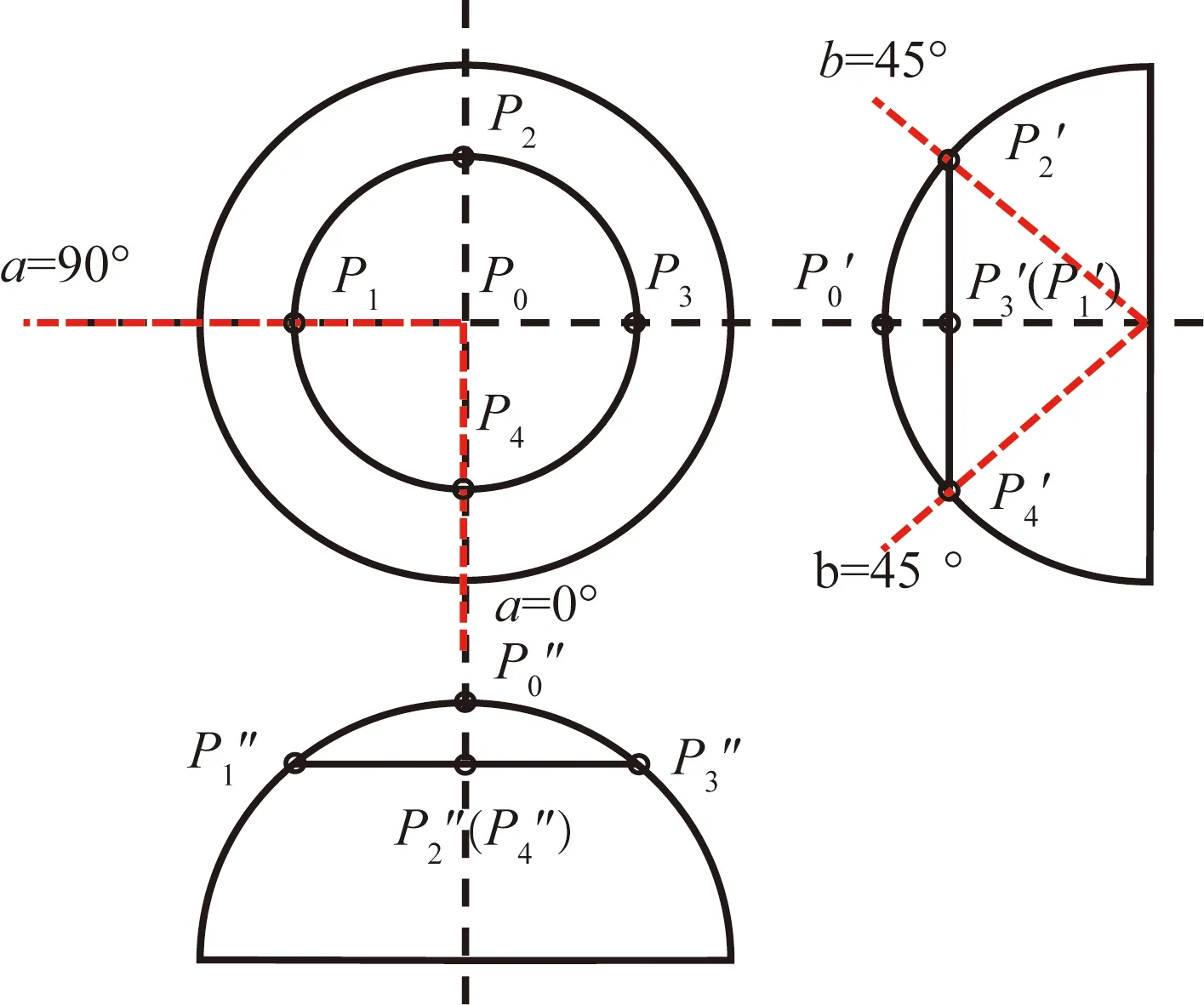
图2 开孔位置示意图
FADS测压孔位置参数如表1所示。
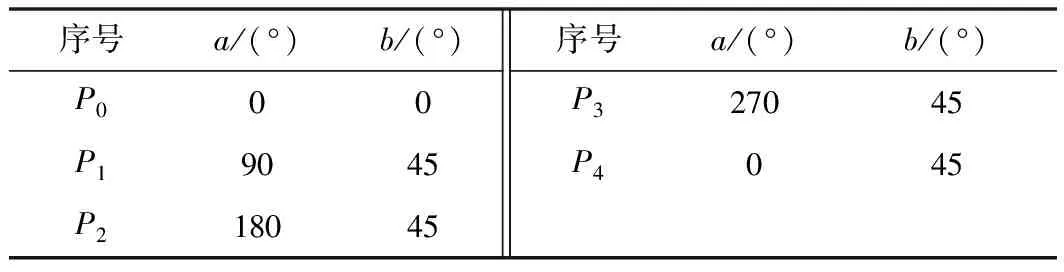
表 1 FADS测压孔位置参数
表1中a为圆周角;b为圆锥角。
由测压孔的位置参数和每个孔的压力值,可列出方程求解动静压:
(1)
式中:pi为第i个测压孔在当前时刻所测压力;σi为第i个孔对应的气流方向;孔的数量为5,即n=5;f为一个单调增函数,其自变量为动静压之比,因变量为修正系数,可由实验或牛顿理论确定,用于修正高马赫数下测压孔数据的偏差。利用5个方程组成的方程组迭代即可求解qc与P∞两个未知数。
为了减少计算量,可使用矩阵伪逆的方法将式(1)化简为
(2)
化简后的方程组在迭代求解qc与P∞时计算更为简单。
基于均匀分布的测压孔,可以使用“三点法”求解攻角和侧滑角数据,但由于三点法涉及反三角函数的计算,在大攻角(α>45°)与小攻角(α<45°)的计算方法不同,原有经典方法[12]仅说明了不同攻角范围时的结算步骤,但未给出相应的判断方法,可以使用如图3所示的攻角计算改进流程进行判断与校正。
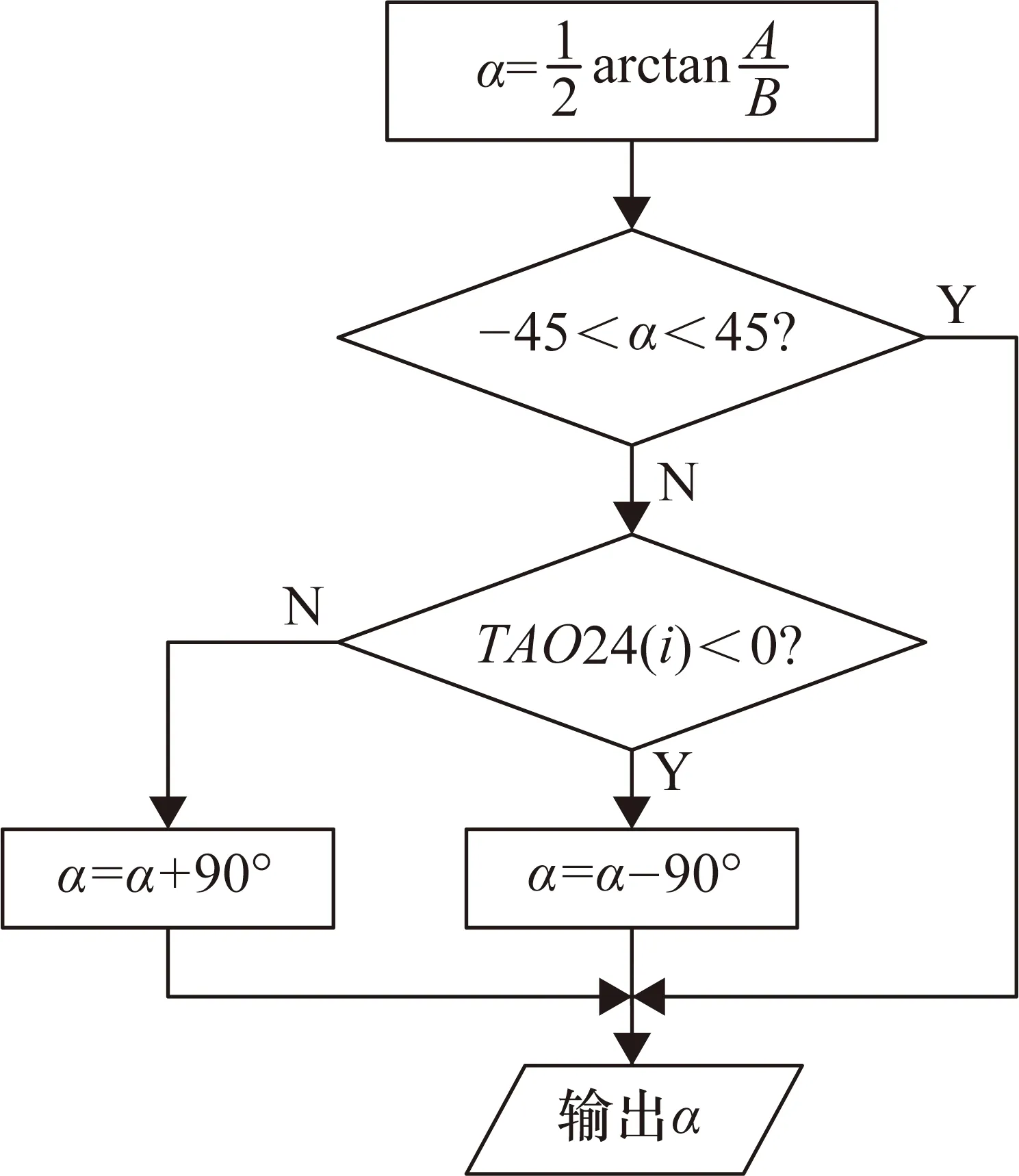
图3 攻角计算改进流程图
图3中TAO24为P2孔与P4孔压力数据的差值。

(3)

(4)
式中:l11为L第1行第1列的数;l12为L第1行第2列的数;以此类推。
1.3 CKF设计与计算
本文提出一种融合IMU数据与FADS数据的大气数据参数估计算法。算法以飞行器飞行速度、加速度、姿态角、角速度为状态量建立系统状态方程;以FADS所测的空速为状态量,建立系统量测方程;考虑到状态方程和量测方程均有较强的非线性特性,采用CKF对马赫数、攻角、侧滑角进行估计,结合测量的动、静压获取较为全面的大气参数。
选取飞行器的三轴速度分量作为状态量X,即:
(5)
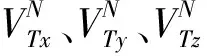
大气的基本风场可以分为平均风、大气紊流、风切变和突风4种形式,其中前两者最为普遍。平均风是风速的基准值,表现为无风或风速、风向不变,此时地速与空速的加速度一致,大气紊流的时间短、速度及其改变量小,也可以认为地速与真空速的加速度基本一致[13],即:
(6)
经整理可得状态方程:
(7)
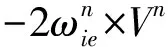
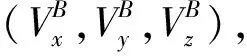
(8)
式中:L为式(3)中的旋转矩阵。
由于地速与真空速的加速度一致,Z可直接由IMU的数据输出,即IMU可提供所需的量测信息。其关系如下:
Z=[X(1),X(2),X(3)]T+v
(9)
式中:X(1)、X(2)、X(3)分别为状态量X的第1~第3项;v为量测噪声向量。因为IMU的数据经惯导系统修正后通常都可以提供较高的角速度,所以此处旋转矩阵直接使用状态量中的(θ,φ,ψ)。
CKF 滤波采用三阶容积法则,用数值积分来近似高斯加权积分,利用一组等权值容积点加权求和来代替加权高斯问题,尤其在高维非线性系统中,可以获得较高的估计精度[14]。针对式(5)~式(9)的非线性系统,CKF滤波算法具体流程如下[15]。
① CKF滤波初始化。
(10)
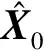
② 时间更新。
对于k-1时刻的状态滤波误差阵,将其因式分解为
(11)
估计容积点为
(12)
式中:
(13)
m为系统向量维数的2倍,这里即为18。
估算状态为
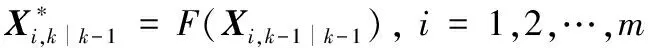

(14)
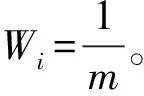
估计误差协方差预测值为

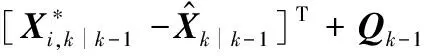
(15)
式中:Qk-1为第k-1时刻的系统过程噪声的协方差矩阵。
③ 量测更新。
将Pk∣k-1分解为
(16)
估计容积点为
(17)
估计量测预测值为
Zi,k∣k-1=h(Xi,k∣k-1)

(18)
式中:h(*)为观测方程,用于取状态量X的第1~第3维。
估计新息协方差矩阵为

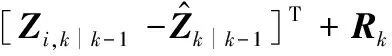
(19)
式中:Rk为第k时刻的测量噪声的协方差矩阵。
估计互协方差矩阵与增益为
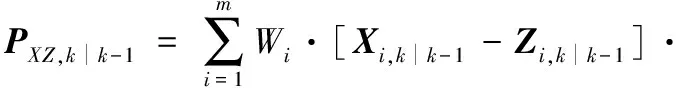
[Xi,k∣k-1-Zi,k∣k-1]T
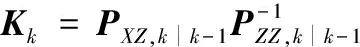
(20)
估计误差协方差为
(21)
④ 滤波值输出。
(22)
2 仿真实验
2.1 仿真参数设置
使用MATLAB对前述CKF算法进行仿真实验,将滤波前测量结果的误差、EKF算法[16]误差和本文提出的CKF滤波的误差进行对比实验,参数设置如下。
飞行高度起始值为1 km,0~200 s(上升段)内上升至巡航高度20 km并保持500 s,最后700~1000 s(下降段)下降至1 km;马赫数上升段从0.1提升至7,巡航段保持不变,下降段由7降为0.1;初始航向角为0°,初始时刻飞行器坐标系与地面坐标系朝向相同,飞行器坐标系0点位于地面坐标系的(0,0,-1000 m)处。飞行总时长1000 s,采样周期T=1 s。
为验证论文算法,设置仿真条件中IMU和FADS的噪声:加速度计0.06 m/s2(3σ);陀螺仪0.03°/s2(3σ);各孔压力数值由马赫数、攻角、侧滑角等参数的实际值求解并添加噪声而得;噪声由加性噪声和乘性噪声组成,服从一阶高斯-马尔科夫过程,相关时间系数0.5,标准差约为20 Pa。
2.2 仿真结果分析
对于上述仿真模型,分别采用前述CKF和文献所述的EKF进行参数估计,图 4和图 5为各滤波方法下滤波前后飞行器三轴速度分量和误差分量的对比。

图4 不同滤波方法估计速度对比

图5 不同滤波方法估计速度误差对比
两种滤波方法对速度均有很好的估计能力。但随着时间增加,EKF在线性化过程中泰勒展开导致非线性部分数据丢失,出现输出结果抖动较大的情况,在100 s时即出现较强的振荡。
两种滤波算法估计的马赫数误差曲线如图 6所示。在整个仿真过程中,CKF的效果都更好。EKF 由于采用了一阶近似的泰勒逼近方法,只能对非线性的系统做到粗略的近似,损失部分精度,且此现象在飞行器高机动性飞行时尤其显著,所以在图6中100 s附近EKF估计的马赫数产生了较大误差。
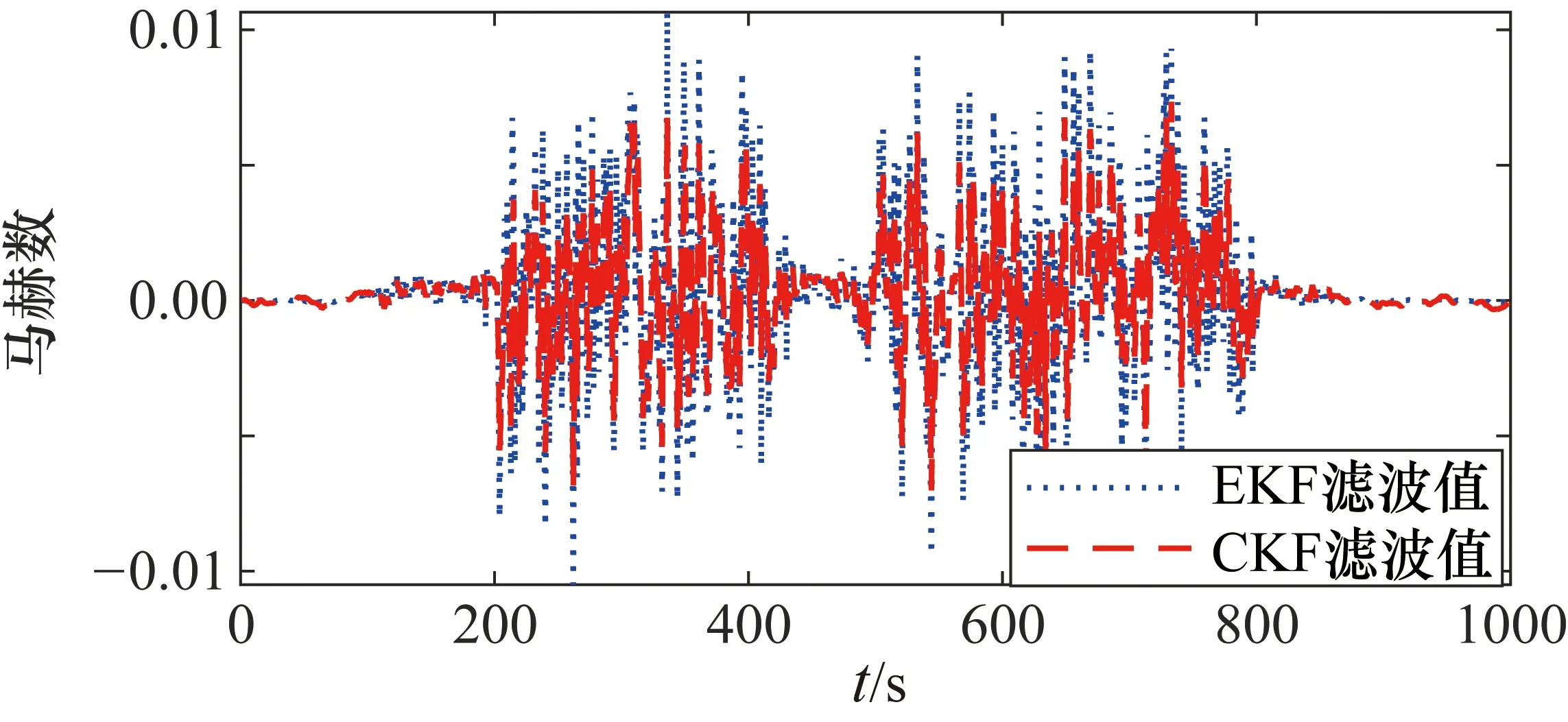
图6 马赫数误差曲线
在马赫数为0.1~7的变化范围下,进行100次的仿真实验,统计各方法估计马赫数误差的最大误差、平均误差和误差标准差,结果对比如表 2所示。

表2 不同方案估计马赫数的误差结果对比
图7和图8分别为不同滤波算法对攻角与侧滑角的估计效果。
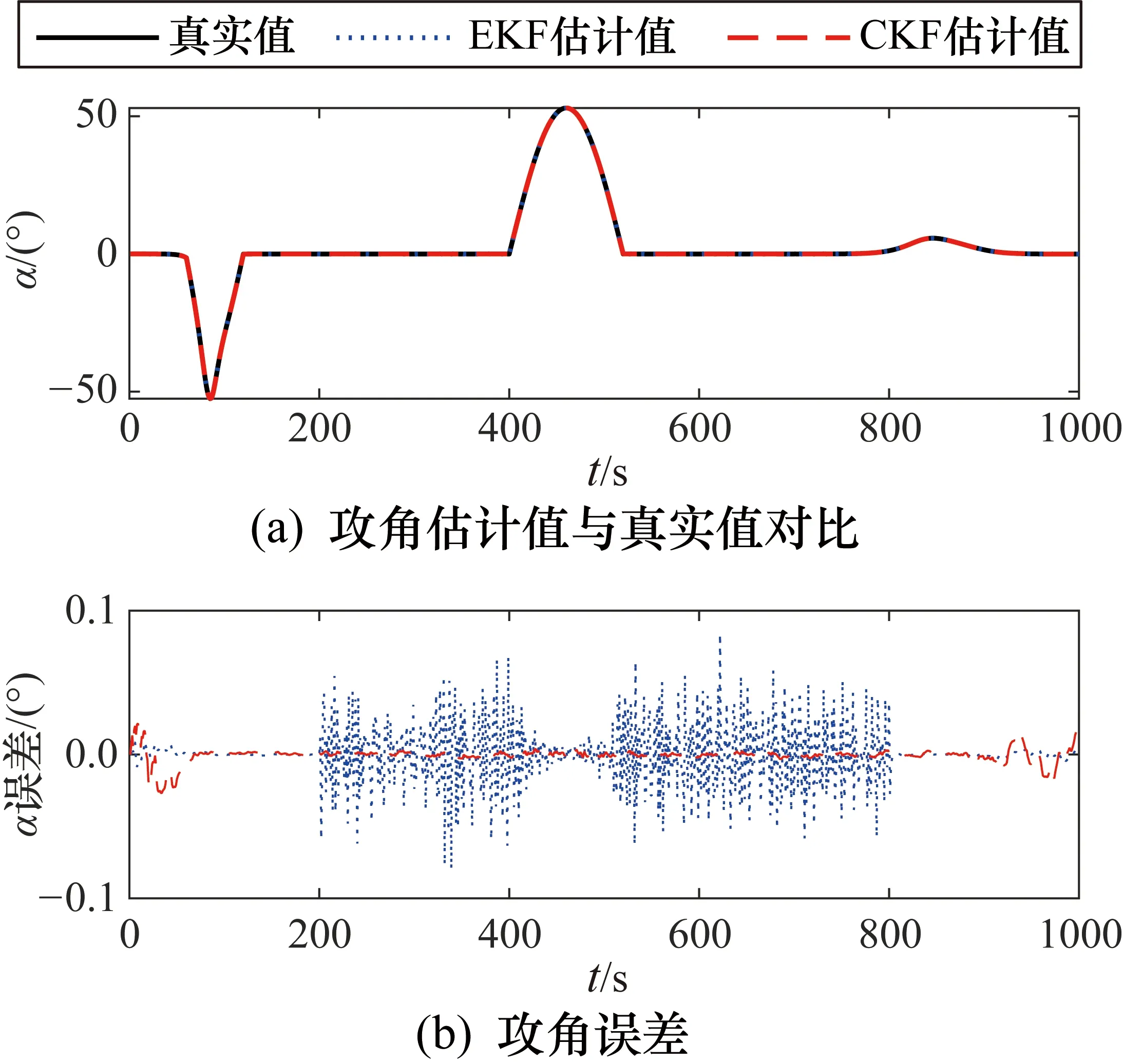
图7 不同方案估计攻角的值与误差
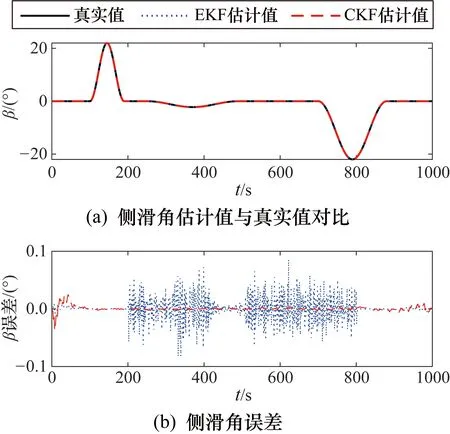
图8 不同方案估计侧滑角的值与误差
从仿真结果可以看出,当攻角范围在±50°,侧滑角范围在±20°的条件下,CKF滤波算法对飞行器的攻角和侧滑角的估计效果更好,尤其在机动状态时具有更强的稳定性。在此条件下进行100次的仿真实验,每次实验持续1000 s,采样周期1 s,表 3和表 4为所有采样点得到的误差的统计结果。

表3 EKF估计α和β的误差结果对比(100次)
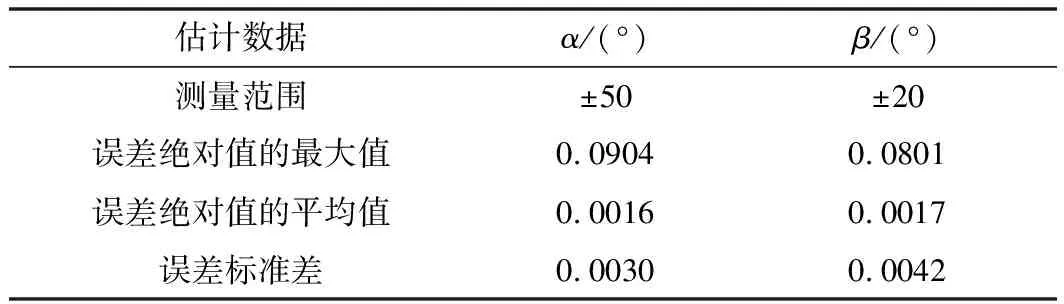
表4 CKF估计α和β的误差结果对比(100次)
从表4中可以看出,利用CKF滤波算法估计的攻角最大误差和侧滑角最大误差,比EKF所得最大误差分别减少了39%和47%。
3 结束语
以容积卡尔曼滤波的FADS和IMU为研究对象,针对现有飞行器面临的马赫数、攻角、侧滑角测量不准确的问题,设计高精度和高可靠性为特色的滤波方法,并采用飞行曲线数据对其进行测试。结果表明该算法能快速准确地计算出各大气参数:攻角误差小于±0.1°,侧滑角误差小于±0.1°,马赫数误差小于±0.01,满足飞行器大气数据估计的基本精度要求。
但是滤波算法在使用时忽略了风场变化等外界扰动带来的不确定性误差,后续需要进一步研究此类偏差存在时的估计方法以提高算法的普遍适用性。

