Phase synchronization and energy balance between neurons＊

Ying XIE ,Zhao YAO ,Jun MA†‡,2

1Department of Physics,Lanzhou University of Technology,Lanzhou 730050,China

2School of Science,Chongqing University of Posts and Telecommunications,Chongqing 430065,China

†E-mail:hyperchaos@lut.edu.cn;hyperchaos@163.com

Abstract:A functional neuron has been developed from a simple neural circuit by incorporating a phototube and a thermistor in different branch circuits.The physical field energy is controlled by the photocurrent across the phototube and the channel current across the thermistor.The firing mode of this neuron is controlled synchronously by external temperature and illumination.There is energy diversity when two functional neurons are exposed to different illumination and temperature conditions.As a result,synapse connections can be created and activated in an adaptive way when field energy is exchanged between neurons.We propose two kinds of criteria to discuss the enhancement of synapse connections to neurons.The energy diversity between neurons determines the increase of the coupling intensity and synaptic current for neurons,and the realization of synchronization is helpful in maintaining energy balance between neurons.The first criterion is similar to the saturation gain scheme in that the coupling intensity is increased with a constant step within a certain period until it reaches energy balance or complete synchronization.The second criterion is that the coupling intensity increases exponentially before reaching energy balance.When two neurons become non-identical,phase synchronization can be controlled during the activation of synapse connections to neurons.For two identical neurons,the second criterion for taming synaptic intensity is effective for reaching complete synchronization and energy balance,even in the presence of noise.This indicates that a synapse connection may prefer to enhance its coupling intensity exponentially.These results are helpful in discovering why synapses are awaken and synaptic current becomes time-varying when any neurons are excited by external stimuli.The potential biophysical mechanism is that energy balance is broken and then synapse connections are activated to maintain an adaptive energy balance between the neurons.These results provide guidance for designing and training intelligent neural networks by taming the coupling channels with gradient energy distribution.

Key words:Hamilton energy;Coupling synchronization;Synapse enhancement;Neural circuit

1 Introduction

Each functional region in the brain consists of a large number of neurons.Eighty percent of neurons in the nervous system are excitatory,while the rest are inhibitory.Biological neurons can be considered as complex charged bodies because of their abundant intracellular ions,and the distribution of field energy is affected by extracellular ions and adjacent neurons.When some neurons are excited,the energy balance in the local region is disturbed due to the external energy injection.As a result,action potentials are induced and propagated for energy release,and the adjacent neurons are coupled by enhancing the synaptic connections for stabilizing the dynamic energy balance.For an isolated generic neuron and a specific neuron (Shilnikov and Cymbalyuk,2005;Herz et al.,2006;Rossant et al.,2011;Yang N et al.,2011;Lin et al.,2020;Liu Y et al.,2020) with special function,the bifurcation parameter and external stimulus can be carefully changed to induce different firing patterns(Szűcs,1998;Shinomoto et al.,2009;Song et al.,2019;Zandi-Mehran et al.,2020).In particular,stochastic disturbances such as noisy driving will induce possible nonlinear resonance(Deng et al.,2009;Blankenburg et al.,2015;Uzuntarla et al.,2015;Andreev et al.,2017;Baysal et al.,2019;Guo et al.,2021) in the neural activities.The activation and release of biophysical functions rely on the cooperation of neurons via different kinds of synapse connections(Pereira et al.,2007;Miller et al.,2015;Liu ZL et al.,2019;Ujfalussy and Makara 2020).The biophysical properties of the coupling channels and synaptic plasticity are important for enhancing the self-adaption of neurons.Appropriate firing modes can be regulated and maintained to maintain energy balance and a synchronous state among neurons.The collective behavior of neural activities has been investigated mainly by detecting the synchronization stability and formation of spatial patterns in the network (Tang et al.,2019;Yang XL et al.,2019;Yao et al.,2019;He et al.,2021;Zhou Q and Wei,2021),in which the coupling channels,local kinetics,and external noisy disturbance can be controlled in a practical way.For more guidance and references about computational neuroscience and biophysical neurons,readers can refer to the studies described in reviews (McDonnell et al.,2015;Wang ZH and Wang,2019;Du et al.,2020;Lin et al.,2021;Yang CZ et al.,2021) and references therein.

For reliable artificial sensors,signal processors in networks,and neural networks composed of biological neurons,the controllability in coupling channels between nodes is critical,and thus the coupling intensity can be regulated adaptively.For example,the coupling intensity between chaotic oscillators and neural circuits can be increased with a constant step in each interval (Liu ZL et al.,2020;Ma et al.,2020)until reaching complete or phase synchronization.When a phototube is used to couple two neural circuits,external illumination is applied to control the photocurrent across the coupling channel and the synchronization approach(Xie et al.,2021a,2021b).When a thermistor is used to connect the output ends of two chaotic circuits,the channel current is controlled by the temperature and the synchronization stability is completely dependent on the external temperature(Zhang XF et al.,2020,2021).When a Josephson junction is used to bridge a connection between two neural circuits,an external magnetic field has a distinct impact on the current along the coupling channel,and thus the synchronization approach becomes dependent on the external magnetic field (Zhang Y et al.,2020).From a dynamic viewpoint,the involvement of the Josephson junction activates effective phase coupling,and this nonlinear coupling is often used in coupled Kuramotor oscillators(Daniels et al.,2003;Trees et al.,2005;Cumin and Unsworth,2007;Breakspear et al.,2010;Ansariara et al.,2020;Wang XB et al.,2021).The abovementioned schemes for synchronization control in chaotic and neural circuits regulate synchronous behavior by injecting and consuming certain energy,and thus the coupled channels become adjustable for maintaining the energy balance between nonlinear circuits.That is,physical schemes can be applied to control chaotic circuits and neural circuits with certain self-adaption.Similar mechanisms in neurons and neural networks can be explored by detecting energy pumping and propagation.Biological neurons can be considered as charged bodies,each maintaining intrinsic electromagnetic field energy.On the other hand,each neuron is surrounded by and connected to adjacent neurons in the same functional region of the nervous system,and the field energy is controlled by the electromagnetic field contributed by other neurons.Any external stimulus will break the energy balance in the local area of the neural network,energy will be propagated to those neurons with lower field energy,and synaptic current will be activated and controlled until it reaches a dynamic energy balance among the neurons.

In this study,a functional neural circuit (Xu Y et al.,2020) is developed by incorporating a phototube and thermistor,such that the output voltage becomes sensitive to external temperature and illumination.After scale transformation,a dimensionless neuron is obtained and its dynamics becomes dependent on light and temperature.The intrinsic Hamilton energy (An and Zhang,2018;Leutcho et al.,2020;Zhou P et al.,2021;Xu L et al.,2022) for this functional neuron is obtained from its physical field energy.When two functional neurons are placed in the same region,the synaptic connection will be activated and enhanced due to distinct diversity in energy.Two isolated spherical shells of different sizes are charged with different amounts of charge and they can keep balance in potential,while the field energy may differ when a wireway is used to connect them.Furthermore,energy flow will be resumed and propagated when the device is connected to a nonlinear circuit,and energy balance becomes prior to the voltage balance.We propose two criteria for activation and enhancement of synapse connections for maintaining energy balance between neurons.We confirm that the synaptic coupling intensity increases until the energy diversity between two neurons is reduced to a finite value.Thus,the two neurons are coupled to share the energy closely and then the coupling is terminated adaptively.These results can address the biophysical mechanism for activation and regulation of synapse connections to neurons and neural networks.They also provide guidance for designing artificial neural networks for intelligent control.

2 Model and scheme

For a simple resistor-inductor-capacitor (RLC)circuit composed of nonlinear electric components,the continuous exchange of magnetic field energy and electric field energy is critical to maintain oscillation.The involvement of an external stimulus is helpful in inducing a chaotic state by adjusting the frequency in the signal source carefully.A phototube can be activated to excite the nonlinear circuit,and the photocurrent across the phototube can be considered a stable signal source.Furthermore,this photocurrentcontrolled circuit can be tamed to reproduce firing modes similar to those of biological neurons,and used as an artificial eye to discuss the relevant dynamics of light-sensitive neurons.A thermistor can be incorporated into one branch circuit such that the output voltage becomes dependent on the temperature.This neural circuit is suitable for describing the temperature effect on excitability and firing modes of neurons.As a result,the biophysical function of the neural circuit can be further enhanced when both a thermistor and a phototube are incorporated into the RLC circuit,and this neuron model can be effective in estimating the dynamics of temperature and illumination synchronously.As presented in Fig.1,a thermistor and a phototube are connected to different branch circuits of the RLC circuit.The activated phototube can emit a continuous photocurrent and the output voltage from the capacitor can show a variety of firing modes.RTdenotes a thermistor and NR a nonlinear resistor.Eis a constant voltage source used as reverse voltage for the ion channel.The linear resistorRShas finite resistance,and photocurrent from the phototube is activated to stimulate this neural circuit.The negative temperature coefficient (NTC) of the thermistor isRT=R∞exp(B/T),whereB=q/K,qis the activation energy,Tdenotes the temperature,andKdenotes the Boltzmann constant.

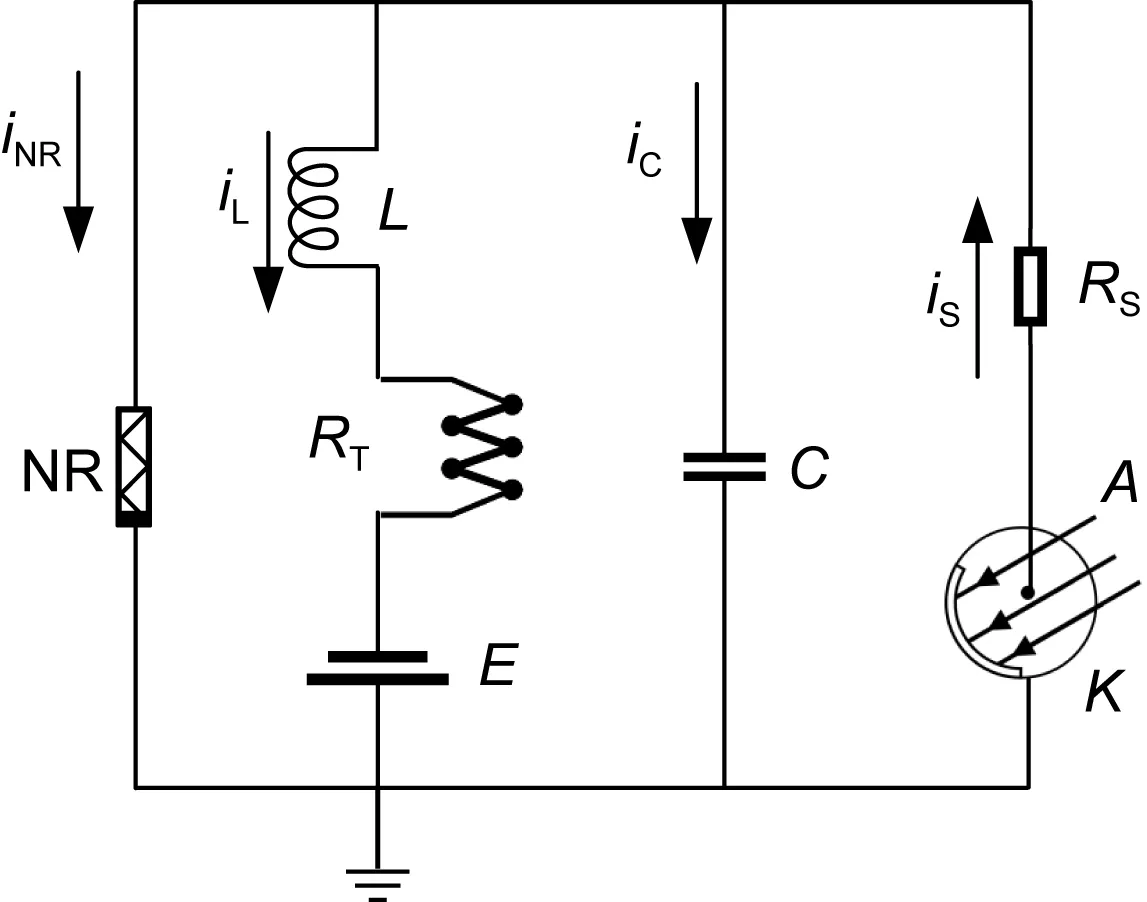
Fig.1 Schematic of a neural circuit composed of a thermistor and a phototube

Generally,a capacitor is suitable for describing the capacitive property of a cell membrane,and an induction coil is suitable for describing the inductive property of a cell.The constant voltageEalong the branch circuit connected to the induction coil is used to approach the reverse potential along the ion channel.In addition,a nonlinear resistor in the neural circuit is often used to represent the nonlinear relation of energy transmission and conversion between magnetic and electric fields during the exchange and propagation of intracellular and extracellular ions.Based on Kirchhoff’s laws,equivalent circuits for Fig.1 can be obtained by

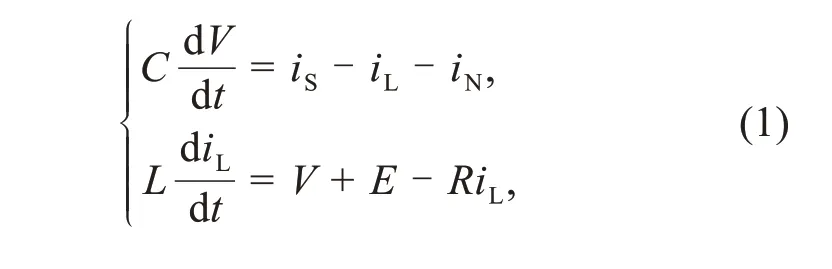
whereVandiLrepresent the output voltage and induction current across the capacitor and induction coil,respectively.The currentiNRacross the nonlinear resistor NR and the photocurrentiSgenerated by the phototube in Fig.1 are described by

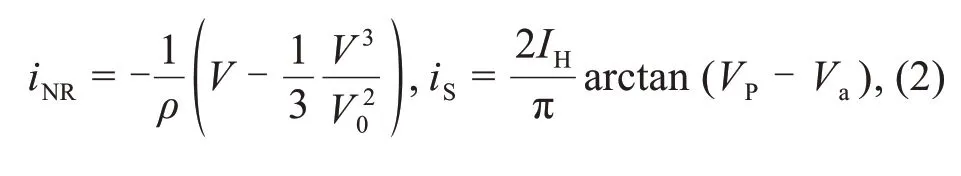
whereρandV0are normalized parameters for the nonlinear resistor,IH,VP,andVarepresent the maximum photocurrent (saturation current),output voltage,and reverse cut-off voltage for the phototube,respectively.For further nonlinear analysis,the variables and parameters for Eqs.(1) and (2) are updated using scale transformation as follows:

The circuit equations for Fig.1 can be mapped into a dimensionless functional neuron model as follows:

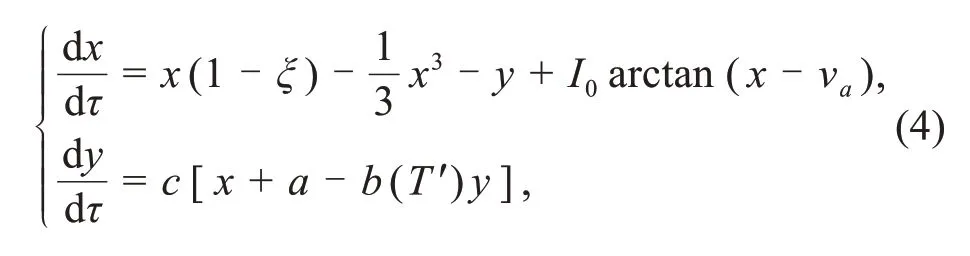
wherexandydenote the membrane potential and channel current in this temperature-sensitive neuron driven by photocurrent,respectively.The two variables are mapped from the output voltage of the capacitor and the induction current of the induction coil(Fig.1).The parameterb(T′) is controlled by external temperature for the thermistorRT,and the firing modes can be adjusted by the channel current across the thermistor.The parameterξis controlled mainly by the linear resistorRS,and the parameterais relative to the constant voltage sourceE.The parameters are often selected asa=0.8,b(T′)=0.2,c=0.1,andξ=0.175,and the external illumination can be adjusted to trigger a photocurrent for inducing mode transition and firing patterns.This neural circuit is driven by a photocurrent when the phototube is completely activated,and the photocurrentIP=I0arctan(x-va),with saturation currentI0and inverse cut-off voltage for the phototube.For a two-variable autonomous system,chaos cannot be induced.The involvement of photocurrent can be considered an external stimulus,and the two intrinsic parameters can be adjusted to induce possible occurrence of chaos in this functional neuron.The field energyWin this neural circuit can be described by the equivalent Hamilton energyHby applying scale transformation to these variables and physical parameters,as follows:

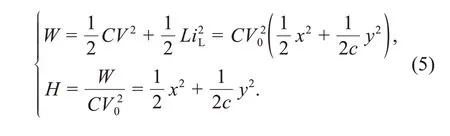
When two identical neurons are excited by different external stimuli and initial values,they will contain different Hamilton energy values.Therefore,the field energy will be shared between neurons,and propagated from one neuron to another until a stable energy balance is reached.During energy propagation between neurons,the firing modes of two neurons are changed and their synapses are awakened for building connections with an adaptive increase in the coupling intensityk.That is,the biological neurons develop possible biophysical criteria for enhancing synapse connections by increasing and regulating the coupling intensity in a self-adaptive way.Energy pumping and propagation will be activated when two neurons show distinct gradient energy(Fig.2).

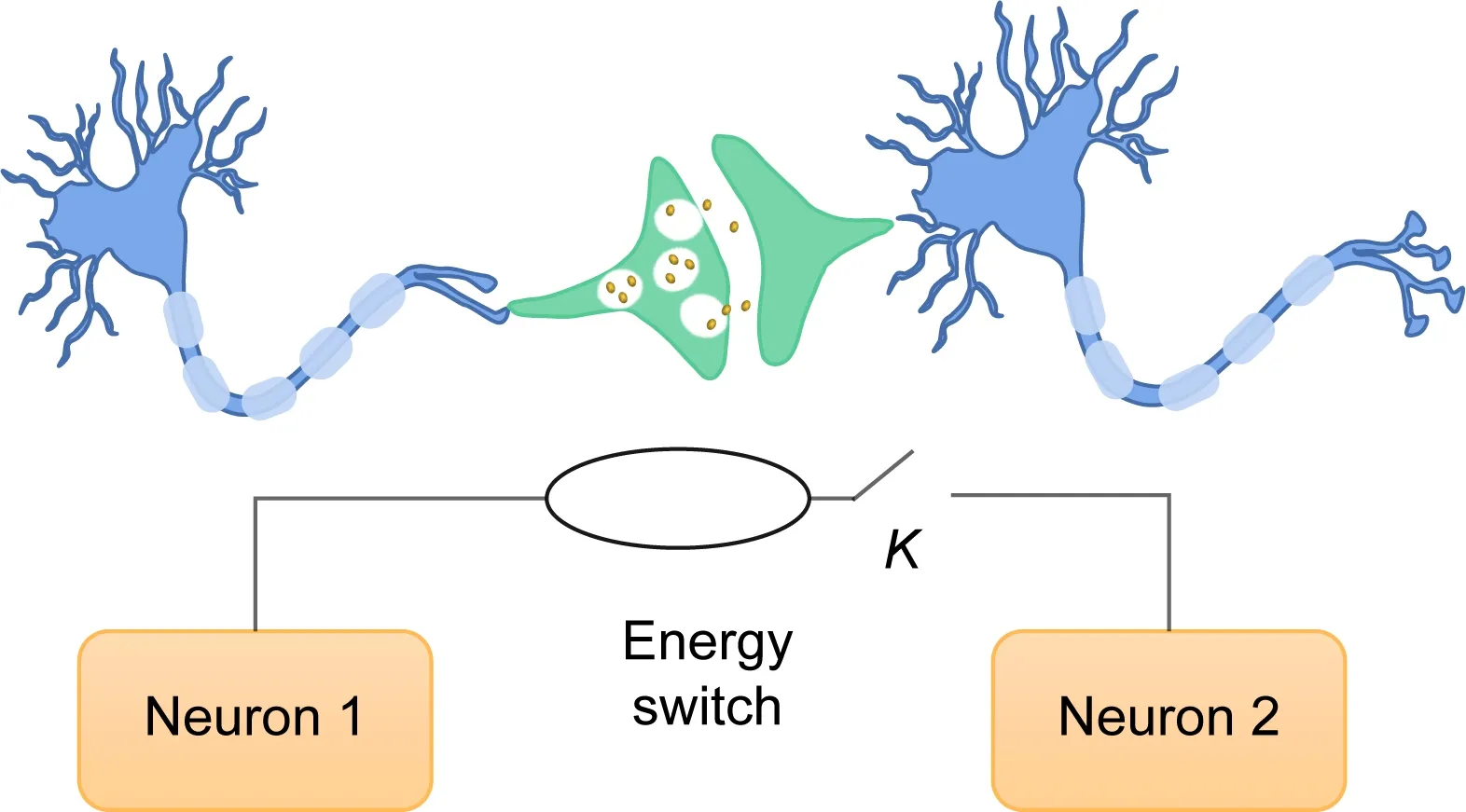
Fig.2 Schematic for neural circuits controlled by energy diversity

Due to the gradient distribution and diversity in the energy field,a synapse connection is activated and further enhanced by changing the coupling intensity until the energy diversity between neurons is reduced to within a finite value.The two neurons are coupled adaptively as follows:

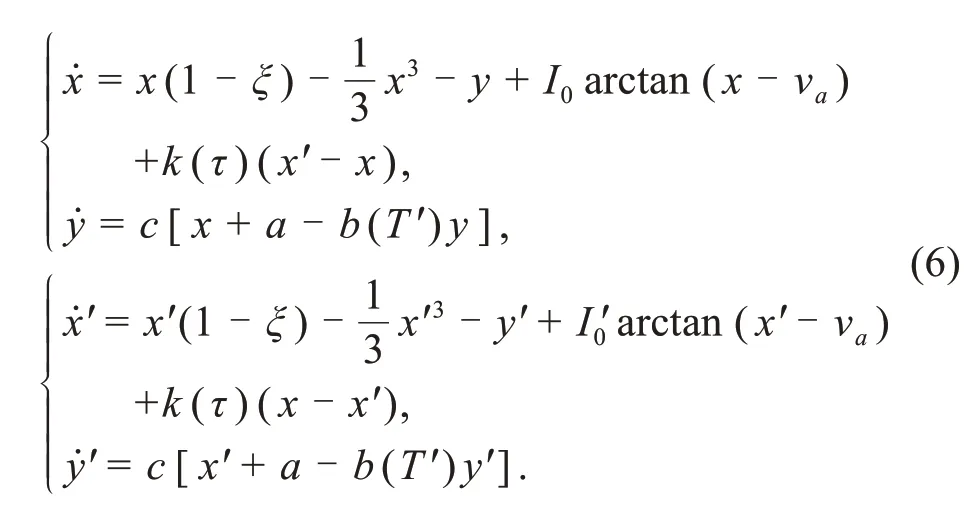
The energy diversity is controlled within a tiny rangeεwhen two neurons reach energy balance within a certain transient period.That is,the synapses are activated and the synaptic connection is further enhanced to reach a certain saturation value until the energy diversity between the neurons is reduced to the tiny valueε.

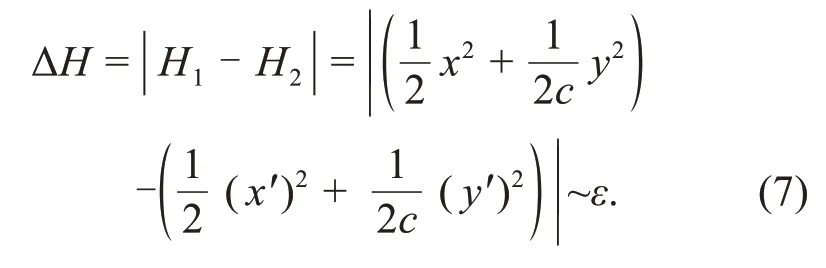
To explore the self-adaptive and synaptic plasticity,two kinds of criteria for synapse activation and enhancement are suggested,and the synaptic intensity is increased before reaching energy balance.The first criterion is similar to the saturation gain criterion,and the coupling intensity is increased with a constant step within the same period,defined by

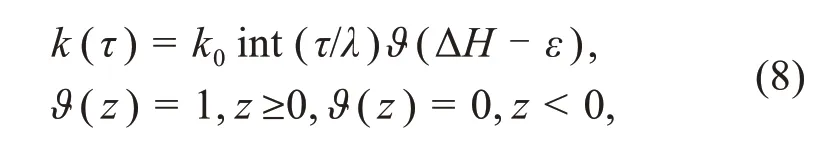
wherek0represents the step value for increasing the coupling intensity,andλrepresents the time interval(period).The operator int() calculates the integer value for timeτwithin each time interval,and the coupling intensity terminates its increase until reaching energy balance,controlled by the Heavside functionϑ().The two neurons will contain the same Hamilton energy when they are coupled to reach complete synchronization;otherwise,energy pumping is continued when the coupling intensity stops to increase below the threshold.Synaptic coupling intensity can also be increased in an exponential way when a synapse connection is enhanced to maintain balance in the field energy.Therefore,the second criterion for synaptic enhancement can be described by

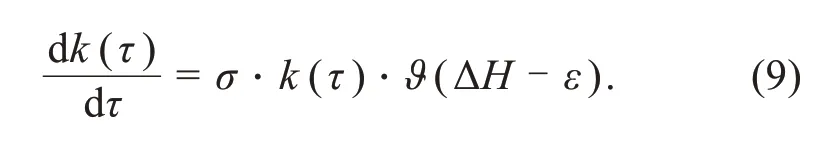
This is similar to the criterion shown in Eq.(8):the coupling intensity is fixed at a saturation value and energy balance is controlled completely.The gainσdenotes the increase in the ratio of the coupling intensity between connected neurons and the initial value for coupling intensity starting from zero.According to Eq.(6),two neurons are coupled with timevarying intensity until stable energy balance or complete synchronization is achieved.Before reaching energy balance,the coupling intensity is increased exponentially ask～exp(στ),and it can be approached byk～στwith a tiny value for the gainσ.For two identical neurons,the error function is often estimated as follows:

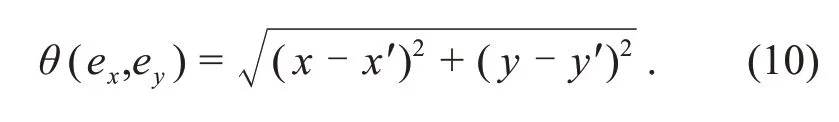
As presented in Eqs.(5) and (6),any diversity in the initial values,temperature,and photocurrents in the two neurons will induce distinct differences in Hamilton energy,parameter mismatch,and excitability in neurons.As a result,synapse connections will be awakened and enhanced in coupling intensity with time,to decrease the difference in energy.The energy pumping and propagation continues before complete synchronization is achieved.However,phase lock and phase synchronization can be stabilized for two or more non-identical neurons.

During the propagation of field energy,the spatial distribution of the electric field fluctuates,and additive noise is induced to further regulate the energy balance and synchronization between neurons.Some previous studies even confirmed that appropriate involvement of noise can enhance the synchronization approach.Therefore,the development and activation of synapse connections will change in the presence of noise.For simplicity,the additive Gaussian white noise with zero average is considered for two neurons.Its statistical properties are defined by

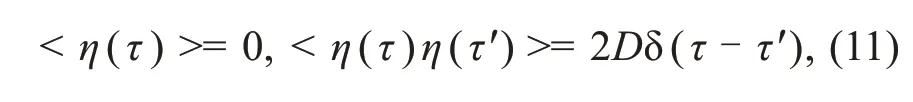
whereDdenotes the noise intensity,and different values are applied to distinguish the activation of synapse connections from the energy balance between neurons.

3 Numerical results and discussion

In this section,the fourth-order Runge-Kutta algorithm is applied to find numerical solutions for the coupled neuron models with time steph=0.01.The transient period for calculation is about 2000 time units.The photocurrent is dependent on two intrinsic parameters,and the changes in the photocurrent will adjust the excitability of the neurons.As a result,the firing modes will be regulated effectively.The Lyapunov exponent spectrum,formation of attractors,and firing patterns are calculated by changing the two parameters in the photocurrent(Fig.3).

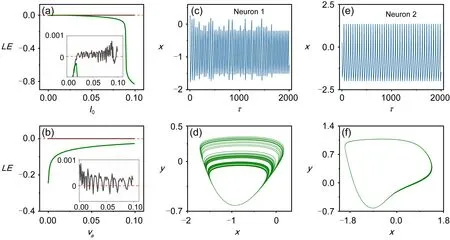
Fig.3 Distribution of Lyapunov exponents,firing patterns,and attractors for an isolated neuron at a fixed temperature:(a)va=0.01;(b)I0=0.087;(c-d)chaotic neuron 1,va=0.01,I0=0.087;(e-f)periodic neuron 2,va=0.01,=0.092

The neuron can be induced to present chaotic and/or periodical firing patterns by taming the intensity of the photocurrent and the inverse cut-off voltage of the phototube.The two neurons become non-identical when they are driven by different photocurrents,such that one of the intrinsic parameters of the phototube shows a slight difference.According to the criterion presented in Eq.(8),the coupling intensity is further increased before reaching energy balance,and the synapse connection is further enhanced(Fig.4).

Fig.4 Evolution of the coupling intensity in synapse connections during energy propagation,with the coupling intensity being controlled by the saturation gain method and different gains and thresholds(ε,k0)being applied:(a)k0=0.1,ε=10-7;(b)k0=0.1,ε=10-5;(c)k0=0.1,ε=10-3;(d)k0=0.001,ε=10-5;(e)k0=0.01,ε=10-5;(f)k0=0.1,ε=10-5

It is confirmed that the energy diversity between two neurons is not compressed to the target range,and energy balance is not realized even when the coupling intensity is further increased with a certain step.As a result,complete synchronization becomes unachievable.For better representation of the synchronization stability,the phase series for the two neurons can be calculated by applying the Hilbert transformation to the sampled time series for their membrane potentials.The evolution and phase error are presented in Fig.5.

As confirmed in Fig.5,the two neurons driven by different photocurrents can reach stable phase lock when the synapse connection is activated and increased with appropriate gain in the coupling intensity.The energy diversity between two neurons is also reduced to a finite value quickly,and energy balance is reached when synaptic coupling is further enhanced.A similar case in the presence of noise is discussed,and the results are shown in Fig.6.

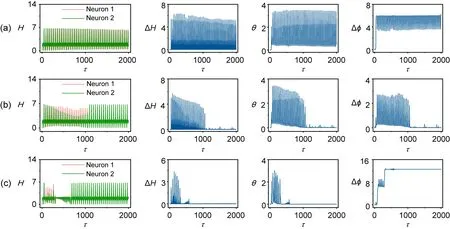
Fig.5 Evolution of Hamilton energy(H),energy error(ΔH),error function(θ),and phase error(Δφ)for coupled neurons:(a)k0=0.0001;(b)k0=0.001;(c)k0=0.005

Fig.6 Evolution of Hamilton energy(H),energy error(ΔH),error function(θ),and phase error(Δφ)for coupled neurons in the presence of noise:(a)D=5;(b)D=10;(c)D=15

The involvement of noise is helpful in maintaining perfect phase synchronization,and energy balance is controlled effectively even when the coupling intensity is increased with a smaller step value,e.g.,k0=0.0001.The reliability of the second criterion is defined in Eq.(9).The coupling intensity is controlled in an exponential way before reaching energy balance(Fig.7).

When the energy diversity is beyond the thresholdε=10-5,the synapse connection is further enhanced by increasing the coupling intensity with different gains forσ.The larger the gain applied forσ,the quicker the increase in the coupling intensity.The coupling intensity increases linearly because the gainσfor the coupling intensity is fixed as a tiny value (Fig.7a).The evolution of energy diversity and the stability of phase synchronization are plotted in Fig.8.

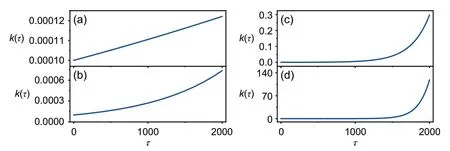
Fig.7 Growth of the synapse connection and evolution of the coupling intensity:(a)σ=0.0001;(b)σ=0.001;(c)σ=0.004;(d)σ=0.008

The sampled time series for the phase error and energy diversity confirm that the two neurons can reach a certain phase lock and complete synchronization,and energy balance is controlled effectively.As a result,the synapse connection is enhanced and coupling intensity is increased when energy diversity is reduced with time.A similar case under noise is discussed,and the results are shown in Fig.9.

When noisy driving is applied with different intensities,complete synchronization and energy balance are corrupted intermittently by applying a smaller gain value forσ.Comparing the results in Fig.9 with those in Fig.6,a stronger noise intensity is effective in controlling the phase lock,and the synapse connection is enhanced due to the continuous exchange and pumping of field energy between the neurons.Phase lock or phase synchronization,rather than complete synchronization,often occurs between non-identical neurons even when the coupling intensity is further increased.Except for the case shown in Fig.8,it is important to confirm whether complete synchronization can be stabilized between two identical neurons driven by the same photocurrent even when different initial values are used.In Fig.10,the saturation gain method is applied to predict the occurrence of complete synchronization between two identical neurons.

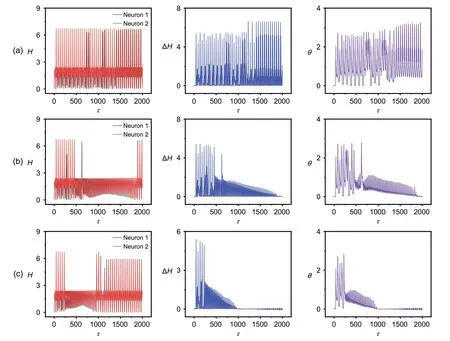
Fig.8 Evolution of Hamilton energy (H),energy error (ΔH),and error function (θ) for coupled neurons: (a) σ=0.001;(b)σ=0.004;(c)σ=0.008

Fig.9 Evolution of Hamilton energy(H),energy error(ΔH),error function(θ),and phase error(Δφ)for coupled neurons in the presence of noise:(a)D=5;(b)D=10;(c)D=15

Comparing the results in Fig.10 with those in Fig.5,the approach of complete synchronization becomes difficult even when phase lock can be realized for two identical neurons selected with the same intrinsic parameters and photocurrent.External noise is also considered,and the results are shown in Fig.11.

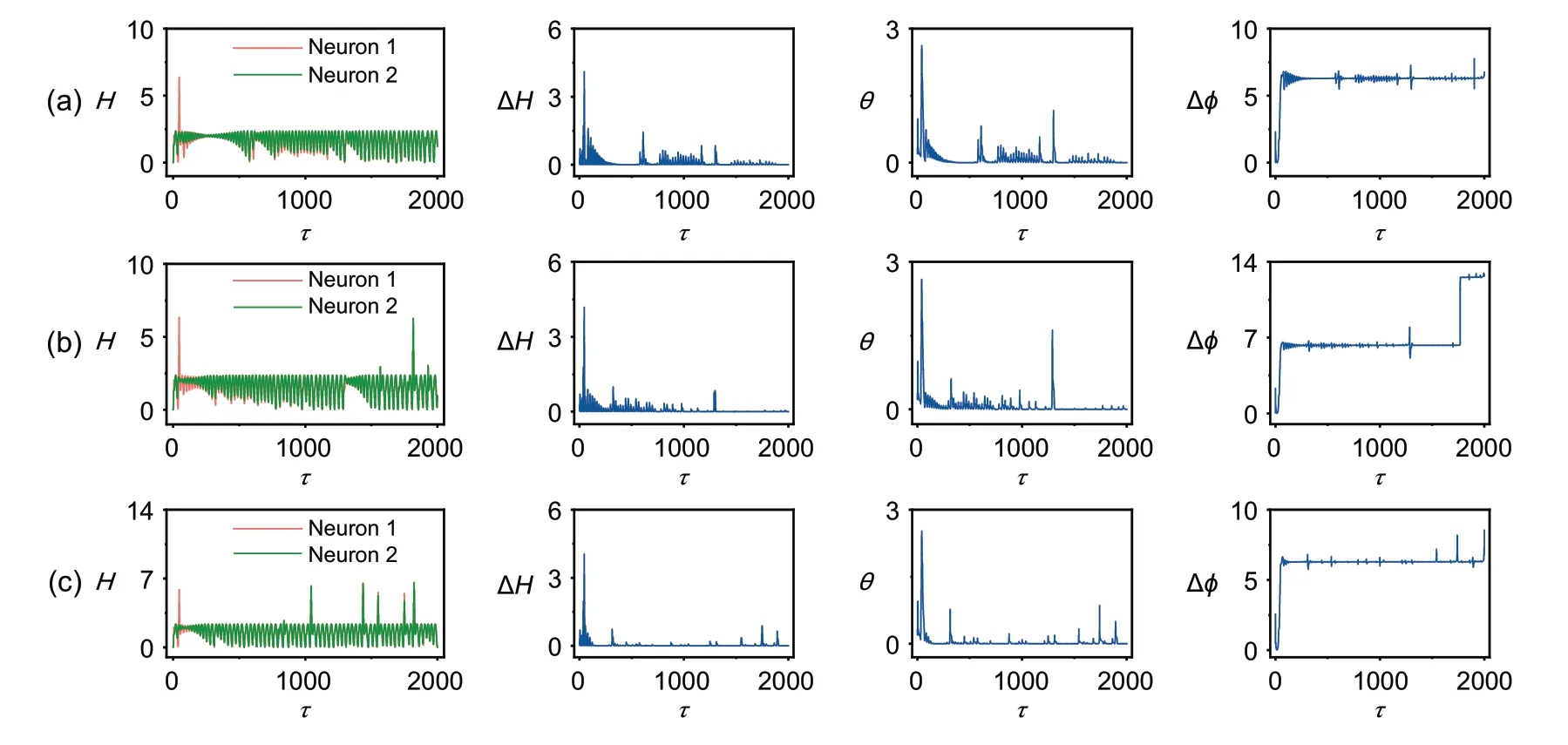
Fig.10 Evolution of Hamilton energy(H),energy error(ΔH),error function(θ),and phase error(Δφ)for coupled neurons:(a)k0=0.001;(b)k0=0.002;(c)k0=0.004

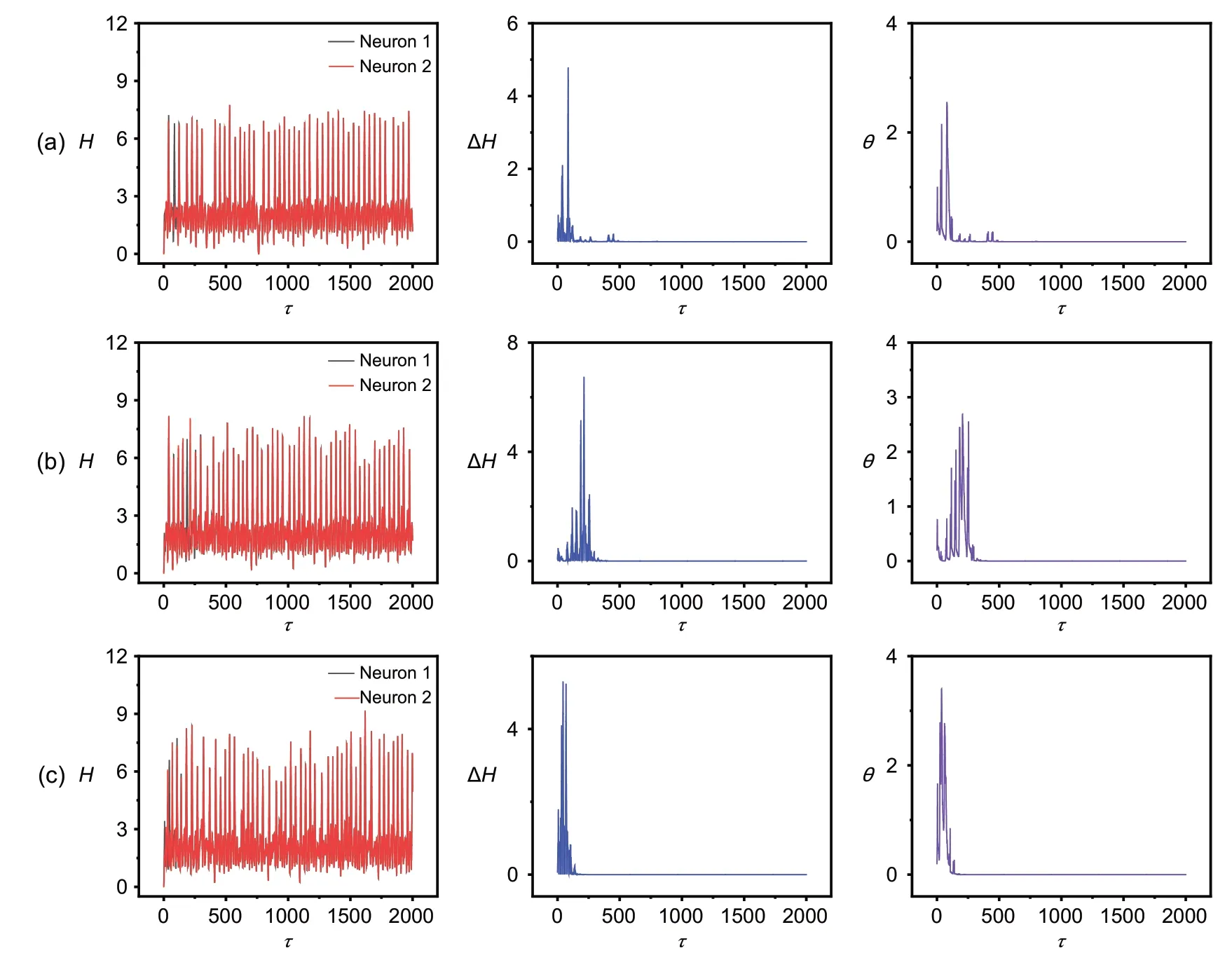
Fig.11 Evolution of Hamilton energy(H),energy error(ΔH),and error function(θ)for coupled neurons in the presence of noise:(a)D=1;(b)D=3;(c)D=5

We find that the involvement of noise is helpful in enhancing the approach of complete synchronization when the synapse connection is controlled by the saturation gain scheme.We discuss a case similar to Figs.8 and 9 when two identical neurons are coupled with an exponential increase in coupling intensity.The results are plotted in Fig.12.

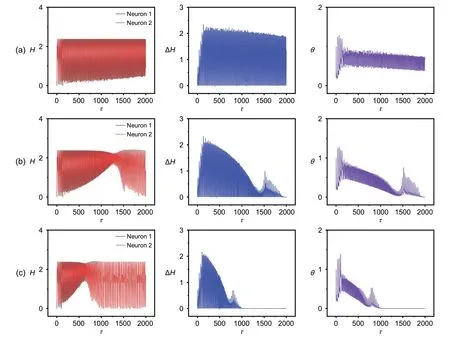
Fig.12 Evolution of Hamilton energy (H),energy error (ΔH),and error function (θ) for coupled neurons: (a) σ=0.001;(b)σ=0.004;(c)σ=0.008

The results are consistent with those in Fig.8 and complete synchronization can be stabilized only when the coupling intensity is increased with appropriate gain.In addition,the two neurons are synchronized to present the same field energy.The effect of noise is also calculated(Fig.13).

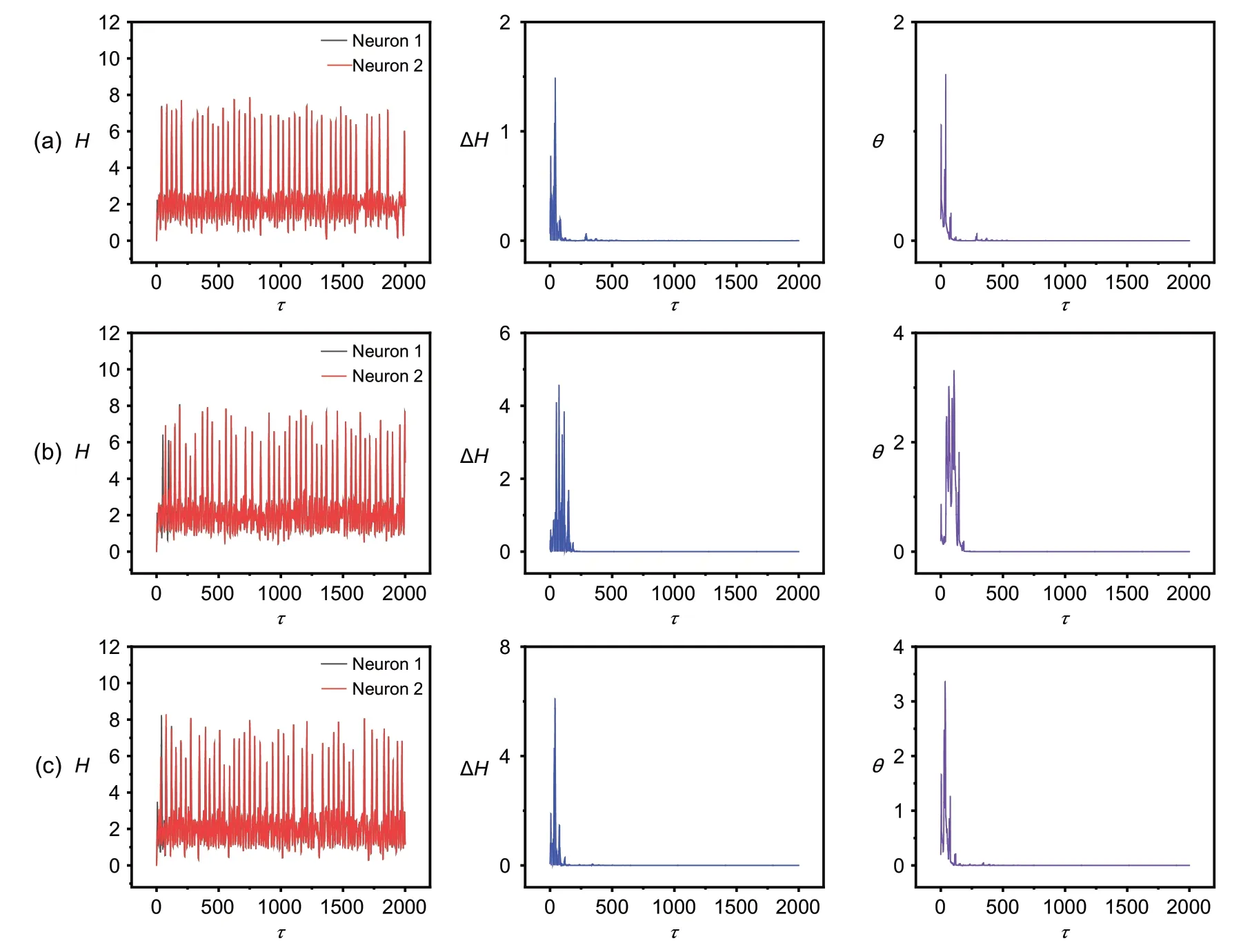
Fig.13 Evolution of Hamilton energy(H),energy error(ΔH),and error function(θ)for coupled neurons in the presence of noise:(a)D=1;(b)D=3;(c)D=5

Our results confirm that the two identical neurons can reach complete synchronization,and energy balance is stabilized even when noise is considered.In particular,the synchronization stability remains resilient to external noise when neurons with energy diversity are coupled to regulate their synapse intensity in an exponential increase with appropriate gains.For the saturation gain scheme,the involvement of noise becomes helpful in stabilizing synchronization between neurons,and energy balance can be controlled completely.

Two different criteria are suggested to explore the activation of synapse connections and enhancement of synaptic coupling when field energy is propagated and shared between neurons.For two nonidentical neurons,phase lock and phase stability can be controlled even in the presence of noise.This is because the energy propagation enables the growth and connection of synapses,and the continuous increase of coupling intensity regulates the collective synchronous patterns for reaching energy balance.From a dynamic viewpoint,the coupling intensity is increased when two neurons show distinct energy diversity.As a result,appropriate coupling intensity is effective in stabilizing synchronization.Energy diversity will be enlarged when two neurons are exposed to different temperature conditions.The parameter mismatch in the neurons will enhance the activation of synapses and their synaptic coupling because of the increased energy diversity.Extensive results confirm that two identical neurons (with the same firing modes) can be controlled to reach complete synchronization even in the presence of noise by taming the coupling intensity carefully.The results explain how a synapse is activated and enhanced to regulate synchronous firing patterns.Phase lock,phase synchronization,and complete synchronization can then be controlled to reach a perfect energy balance between two or more neurons in neural networks.In addition,biological neurons can be connected with different types of synapses.Synchronous behaviors in the neural networks are dependent on the firing modes and biophysical properties (Uzuntarla et al.,2019) in the coupling channels and synapse connections.The results from our study provide some new insights to reconsider the synaptic function and development of hybrid synapses in neural networks.Our discussions also suggest that external field energy can be used to guide and control the synapse function,and thus neurons can be tamed to present appropriate firing modes.

4 Conclusions

In this study,two criteria for activating and enhancing synapse connections to neurons with energy diversity are proposed.Each neuron contains certain field energy,and any external stimulus will change its firing mode and field energy.With more neurons,the field energy for each neuron is dependent on its intrinsic biophysical property and also the electromagnetic field emitted from other neurons.All neurons are kept in energy balance with their synapses being tamed under field coupling.Any stimulus will disturb the energy balance and the energy will be propagated and shared by those neurons with lower field energy without external stimuli.As a result,the synapse connections can be awakened and synaptic coupling is further increased with time until a dynamic energy balance is achieved.Based on a simple functional neuron model,the two control schemes are used to discuss the energy propagation and synchronization approach between two different neurons.The results confirm that they can reach synchronization and phase lock even when considering the effect of additive noise on the membrane potential,and energy balance can be well regulated when synaptic coupling is further increased.These results provide new insights to understand the synaptic function and the biophysical mechanism for activating synapse connections to neurons.Injection of external energy can be used to regulate the collective behavior of neural networks effectively.

Contributors

Jun MA designed the research.Ying XIE and Zhao YAO processed the data.Jun MA drafted the paper.Zhao YAO helped organize the paper.Zhao YAO and Jun MA revised and finalized the paper.

Compliance with ethics guidelines

Ying XIE,Zhao YAO,and Jun MA declare that they have no conflict of interest.