A novel grey wolf optimizer and its applications in 5G frequency selection surface design＊#

Zhihao HE ,Gang JIN ,Yingjun WANG†‡

1National Engineering Research Center of Novel Equipment for Polymer Processing,South China University of Technology,Guangzhou 510641,China

2Key Laboratory of Polymer Processing Engineering of the Ministry of Education,South China University of Technology,Guangzhou 510641,China

3Guangdong Provincial Key Laboratory of Technique and Equipment for Macromolecular Advanced Manufacturing,South China University of Technology,Guangzhou 510641,China

†E-mail:wangyj84@scut.edu.cn

Abstract:In fifth-generation wireless communication system (5G),more connections are built between metaheuristics and electromagnetic equipment design.In this paper,we propose a self-adaptive grey wolf optimizer (SAGWO) combined with a novel optimization model of a 5G frequency selection surface (FSS) based on FSS unit nodes.SAGWO includes three improvement strategies,improving the initial distribution,increasing the randomness,and enhancing the local search,to accelerate the convergence and effectively avoid local optima.In benchmark tests,the proposed optimizer performs better than the five other optimization algorithms: original grey wolf optimizer (GWO),genetic algorithm (GA),particle swarm optimizer(PSO),improved grey wolf optimizer (IGWO),and selective opposition based grey wolf optimization (SOGWO).Due to its global searchability,SAGWO is suitable for solving the optimization problem of a 5G FSS that has a large design space.The combination of SAGWO and the new FSS optimization model can automatically obtain the shape of the FSS unit with electromagnetic interference shielding capability at the center operating frequency.To verify the performance of the proposed method,a double-layer ring FSS is designed with the purpose of providing electromagnetic interference shielding features at 28 GHz.The results show that the optimized FSS has better electromagnetic interference shielding at the center frequency and has higher angular stability.Finally,a sample of the optimized FSS is fabricated and tested.

Key words:Grey wolf optimizer;Fifth-generation wireless communication system (5G);Frequency selection surface;Shape optimization

1 Introduction

Nature-inspired optimization techniques have made significant progress since they emerged in recent decades.They have a remarkable ability to solve nonconvex and multi-dimensional problems in engineering and science.The prevalent nature-inspired algorithms can be divided into three categories: evolutionary algorithms (EAs) (Carrasco et al.,2020),physics-based algorithms(An et al.,2015),and swarm intelligence(SI)based algorithms(Phan et al.,2020).Different natural phenomena inspire the design of the three types of algorithms.The grey wolf optimizer(GWO) is an SI optimization algorithm proposed by Mirjalili et al.(2014).It imitates the social behavior and hunting mechanism of grey wolves and learns from their intelligent approach to search for prey.GWO is a flexible and straightforward algorithm like other well-known population-based algorithms such as particle swarm optimizer (PSO) (Gutiérrez et al.,2011),monarch butterfly optimization (MBO) (Wang et al.,2019),differential evolution (DE) (Zou et al.,2011),moth search algorithm (MSA) (Wang,2018),dragonfly algorithm (DA) (Mirjalili,2016),glowworm swarm optimization (GSO) (Aljarah and Ludwig,2013),colony predation algorithm (CPA) (Tu et al.,2021),and Harris hawks optimization(HHO)(Heidari et al.,2019).In GWO,wolves can share information about the search space to find the best solution and avoid local optima.GWO has fewer operators compared to other evolutionary techniques and uses fewer parameters to explore the search space.Therefore,it can reduce computational cost for a given optimization problem.Because of these advantages,GWO has been applied to several fields and has shown favorable optimization results.For example,it has been successfully used in photovoltaic systems (Mohanty et al.,2016),interconnected power systems (Shakarami and Davoudkhani,2016),medical diagnosis (Li Q et al.,2017),welding industry,water resource optimization (Dehghani et al.,2019;Donyaii et al.,2020),antenna arrays (Khan et al.,2018),and truck scheduling problems(Peng and Zhou,2019).

In GWO,the search process,guided by three best wolves,can achieve a high convergence speed.However,this model impedes global exploration.GWO still suffers from the stagnation of local optima.Therefore,many researchers have modified GWO to better balance exploitation and exploration.For example,Cai et al.(2019) proposed an improved GWO,combined with a kernel extreme learning machine,to provide better optimization results.Hu et al.(2021) developed a GWO variant enhanced with a covariance matrix adaptation evolution strategy,Levy flight mechanism,and orthogonal learning.Yu et al.(2022) proposed a multi-stage GWO that optimizes GWO in three steps.The multi-stage GWO can better avoid local optimum trap than GWO.Gupta and Deep(2019) proposed a novel random walk to improve searchability.The novel GWO is efficient and reliable for real-life optimization problems.To exploit the potential of GWO,we propose a self-adaptive grey wolf optimizer (SAGWO),which includes three improvement strategies: (1) improving the initial distribution,(2)increasing the randomness,and(3)enhancing the local search.The aim of improving the initial distribution strategy is to acquire a better primary population.Improving the randomness strategy changes the hunting behavior and convergence steps to improve searchability.Three methods of changing convergence steps have been studied to determine the most appropriate SAGWO.Enhancing the local search strategy is used in the last stage of the algorithm to maximize exploitation.

The structural optimization problems of electromagnetic communication equipment,e.g.,antennas and frequency selection surface (FSS),are usually difficult to solve with traditional gradient-based methods,since it is difficult to obtain the derivative between the objective function and the design variables.Therefore,researchers use non-gradient optimization methods (e.g.,GWO) to solve such problems.Boursianis et al.(2019) incorporated GWO into a dual-band E-shaped patch antenna design.Goudos et al.(2019)combined the Jaya optimization algorithm and GWO to optimize a fifth-generation wireless communication system (5G) E-shaped patch antenna.Saxena and Kothari (2016) compared GWO with other metaheuristic algorithms to design array antennas.Results showed that GWO can provide considerable enhancements.Liu et al.(2020)proposed a dynamic cooperative GWO and used it in array antenna design.In this study,the proposed SAGWO,with intensified global searchability,is adapted to electromagnetic equipment optimization to design a new type of electromagnetic equipment,5G FSS.

5G FSS is used for electromagnetic interference(EMI) shielding in the micro/millimeter-wave band due to its bandpass and bandstop characteristics(Li D et al.,2017,2018;Paul et al.,2021).In most cases,FSS is an array structure composed of a series of periodically arranged passive resonant units,which have selective permeability to electromagnetic waves in different frequency bands.FSS has many advantages such as small volume,convenient design,and simple manufacturing operation due to its special structure.The work function of FSS is determined by the structure and configuration of the units (Parker et al.,2001).Therefore,traditional FSS optimization can be regarded as a multi-parameter optimization problem of FSS units,and is solved mostly by common meta-heuristic algorithms such as the genetic algorithm(GA) (Villegas et al.,2004;Ge et al.,2007;Crevecoeur et al.,2010) and PSO (Genovesi et al.,2006).As a novel meta-heuristic method,our proposed SAGWO has great potential to solve the FSS optimization problem.In this study,we solve the FSS optimization problem based on the following three aspects: First,a novel FSS optimization model is proposed based on unit nodes;Second,SAGWO is introduced into the FSS design process to design a double-layer ring FSS that works at 28 GHz;Finally,a sample of optimized FSS is fabricated and tested to verify the validity of the novel method.

2 Grey wolf optimizer

GWO manifests the behaviors of grey wolves,including their social hierarchy,encircling,hunting,attacking,and searching for prey.In this section,these five steps of GWO are introduced.

1.Social hierarchy

In the wolf society,all individuals can be categorized into four types,α,β,δ,andω,according to their status.The mathematical description of different roles is that the three individuals with the best solutions in the last iteration are treated as belonging toα,β,andδcategories,and all the remaining solutions are regarded asω.The subsequent process preserves these categories.

2.Encircling prey

To describe the step of encircling prey,the following equations are used:

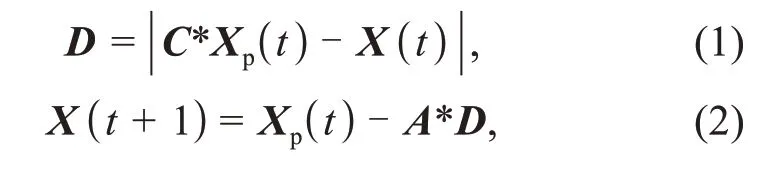
wheretandt+1 represent two adjacent iterations,“*”is the Hadamard product operator,Xprepresents the position vector of the prey,Xindicates the position vector of a grey wolf,and |·| is the absolute value operator.AandCare coefficient vectors.The decreased distances between the wolves and their prey depend on vectorsAandD.VectorsAandCare calculated as follows:

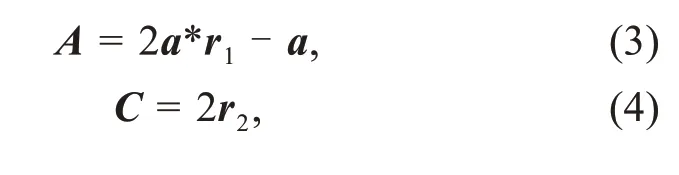
whereais a vector whose elements linearly decrease from 2 to 0 throughout the iteration,andr1andr2are the vectors whose elements are ranged in[0,1].

3.Hunting

In the hunting stage,wolves find the location of the prey and then encircle the prey according toα,β,andδ.The mathematical equations that simulate the hunting process fromttot+1 generation are given by Eqs.(5)-(7):

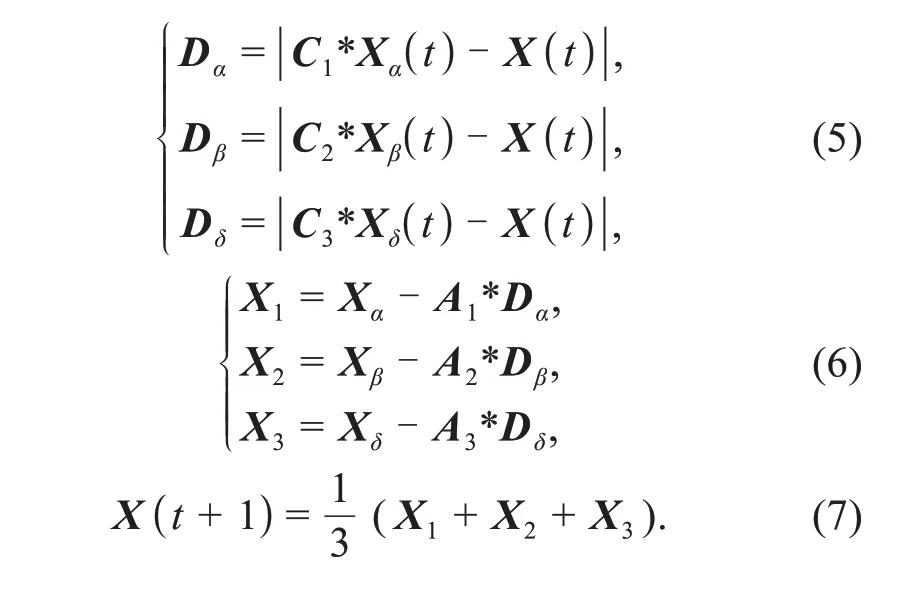
After the positions of all wolves are updated based on the above equations,they are sorted by the fitness calculated from the objective function.Then the three wolves with the best results are set asα,β,andδ,separately.

4.Attacking prey

Ais in the range of [-a,a] and changes withawhose elements decrease from 2 to 0 during the search process.This simulates the behaviors of wolves closing in and attacking prey.When the absolute values of all the elements ofAare less than 1,grey wolves actively approach their prey and prepare for the final attack.

5.Searching for prey

The search efficiency of GWO is affected byα,β,andδ.When |A|≥1 (i.e.,the absolute values of all the elements ofAare not less than 1),wolves tend to search for better prey in the search space.This situation occurs more frequently in the early development phase of the algorithm.C,a random vector whose elements are in the range of [0,2],is another critical parameter for global search.It offers random weights for exploration and alleviates the local optimum problem.Fig.1 is an illustration of the original GWO in a two-dimensional(2D)situation.

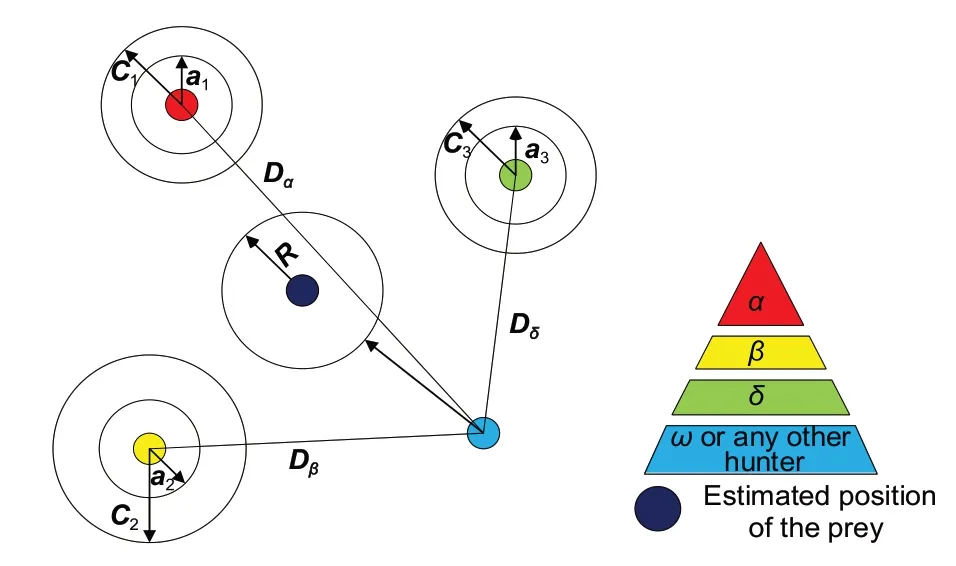
Fig.1 Illustration of the grey wolf optimizer(GWO)

3 Self-adaptive grey wolf optimizer

GWO is a direct and valid swarm intelligence algorithm.GWO needs only to determine the population size and the maximum number of iterations before solving an engineering problem.Compared with other swarm intelligence algorithms,GWO requests fewer parameters in the whole search process and has a more straightforward implementation.

However,experimental analysis shows that GWO is prone to local optima in some cases due to the insufficient exploration ability of grey wolves.In unimodal tests,the increase in dimensionality slows down the convergence of GWO.Avoiding local optima and accelerating convergence are two research priorities for GWO.Hence,in this study,we propose three improvement strategies to enhance the explorative ability of GWO.Fig.2 shows the three strategies: Fig.2a shows the improvement of the initial distribution strategy,Fig.2b shows the improvement of the randomness strategy,and Fig.2c shows the improvement of the local search strategy.The novel GWO is selfadaptive;it can change its parameters in response to different situations.Therefore,we call it SAGWO.

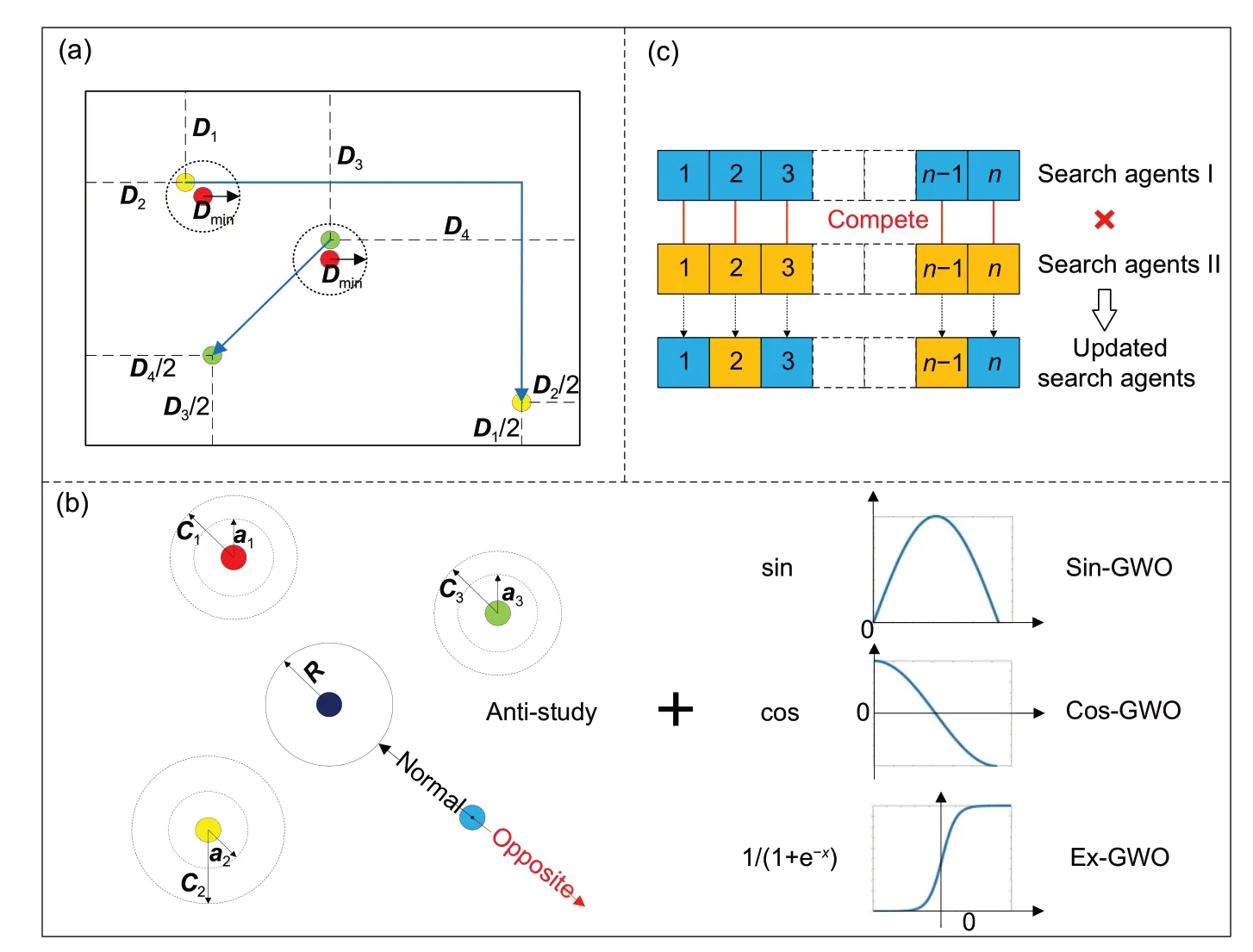
Fig.2 Three improvement strategies for SAGWO: (a) improvement of the initial distribution strategy;(b) improvement of the randomness strategy;(c)improvement of the local search strategy

3.1 Improved initial distribution

The initial population,especially the positions of the three leaders,has an obvious influence on the early exploration of GWO.If,by coincidence,the leaders enter a local optimal solution at the beginning of the algorithm,they may fail to update in subsequent iterations.This will affect the efficiency of the entire optimization process and the accuracy of the final result.An improved initial distribution strategy based on the Euclidean distance is introduced at the early stage of the algorithm to avoid this problem.The idea of this method is to disperseα,β,andδproperly so that the algorithm has better performance during initialization.After randomly obtaining the initial population,the algorithm calculates the Euclidean distanceEpbetweenαand the remaining individuals by Eq.(8):

wherenrepresents the dimension of the problem,Epis a limit value to judge whetherα,β,andδcluster,and the value ofEpis determined by the specific optimization problem.xpiis theithposition variable of the prey,andxaiis theithposition variable of the leader wolf.In the examples,one-tenth of the maximum Euclidean distance between the upper and lower limits is used as the limit value,as shown in Eq.(9):

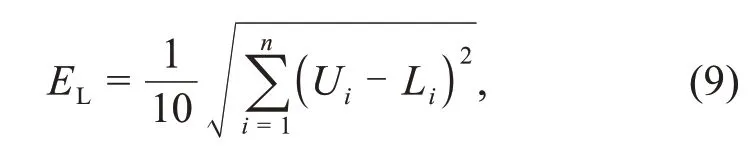
whereU=(U1,U2,…,Un) is the upper limit andL=(L1,L2,…,Ln)is the lower limit.

If an individual’s Euclidean distance is less than the default limit valueEL,the individual is moved in the following way:

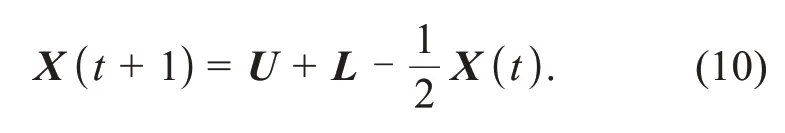
Eq.(10) disperses the initial population and avoidsα,β,andδall falling into the same local optimum.Simultaneously,the movedβandδare closer to the boundary of the search range,which enhances the algorithm’s ability to search at the boundary.A 2D schematic is shown in Fig.2a.

3.2 Increased randomness

Appropriately increasing the randomness of algorithm iteration is an effective method for enhancing the exploration of the algorithm and avoiding local optima.In the original GWO design,Cis a random variable throughout the process,which imitates the natural environment’s influence on the hunting of wolves.AlthoughCprovides randomness that emphasizes GWO exploration,the evolutionary direction of GWO still constantly approaches the direction of the prey indicated by the leaders,lacking the ability to break out of this trend.

The proposed increased randomness strategy consists of anti-study and random step size.Anti-study provides the ability to eliminate the leaders’control,and wolves can reverse movement during the algorithm convergence process.The random step size strategy changes the linear step sizea,mentioned in Section 2.2,to non-linear.Fig.2b is an illustration of the increased randomness method.

The proposed anti-study strategy offers the reverse movement in the agent moving process.Even if the leaders fall into local optima,reverse movement can provide the ability to search for better results again.The specific steps are given in Eq.(11).When the individual updates its position,it is likely to move in the opposite direction to the current potential prey.The optimization situation at that time adjusts the probability of the occurrence of reverse movement.

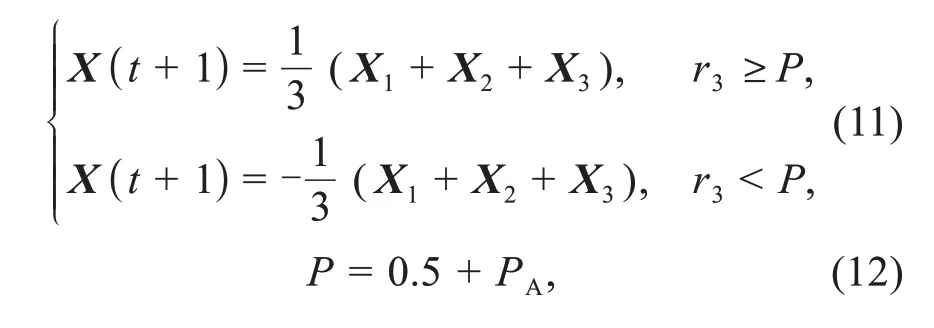
wherer3is a random parameter in the range of[0,1],andPis the probability of reverse movement.The initial value ofPAis 0,and equals 0.2 whenαis stagnant during the exploration phase.This improves the algorithm’s ability to break out of local optima.

The convergence process of the algorithm is driven by linear step sizea.In GWO,the elements ofalinearly decrease from 2 to 0.At the early stage of the algorithm,when the elements ofaare close to 2,the algorithm has a larger step size to increase exploration.When the elements ofadecrease to 0,a smaller step size tends to emphasize exploitation.However,the linear reduction step size is not required when dealing with practical problems.Adding randomness to the reduction parameteracan cooperate with antistudy to mitigate the local optima.Three types of functions have been studied to determine the most appropriate randomastrategy:

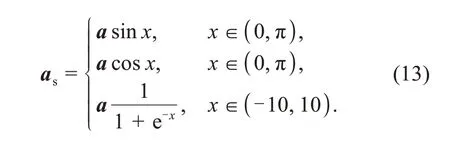
Eq.(13) shows three introduced functions.The parameterareduction process is transformed into a non-linear formas.Parameterxis a random variable.Subsequently,asis used in SAGWO:

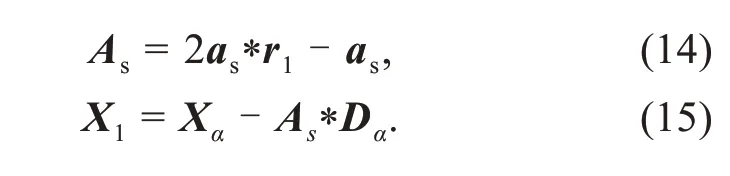
In Section 5.2,three types ofasare tested by 15 benchmark functions.

3.3 Enhanced local search

Based on the “no free lunch theorem,” no metaheuristic can solve all types of problems.GWO,with an increased randomness strategy,emphasizes exploitation,but partly sacrifices the performance of exploration.

To balance the exploitation and exploration of SAGWO,we propose an enhanced local search strategy in the final stage of the algorithm.This strategy causes each individual to be calculated twice within an iteration,using Eqs.(14) and (15) and Eqs.(5)and(6).Adding an extra calculation takes the original GWO back to the search process so that each individual has two iteration results.One result is from the traditional part,and the other is from the novel part.Only a better result can be formed in the next population (Fig.2c).This method can counteract the negative effect of an increased randomness strategy and improve the accuracy of local exploitation.

GWO requires a small number of search individuals to complete the optimization,which improves the algorithm’s efficiency.The repeated calculation increases the overall computation time,but it is controlled byaand performes only when the elements ofaare less than 0.5.So,extra computation time generated by the novel algorithm is controllable.Combined with the increased randomness strategy,SAGWO has a better overall performance.The implementation of SAGWO is depicted in Fig.3.

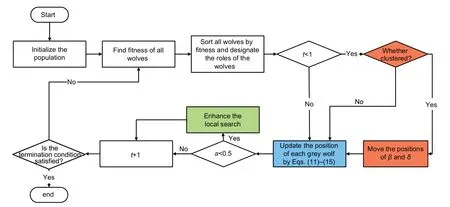
Fig.3 Flowchart of the SAGWO algorithm (The three strategies are highlighted in red,blue,and green.References to color refer to the online version of this figure)

3.4 Time complexity analysis

Time complexity of the proposed SAGWO is determined by eight steps:(1) initialization,(2) fitness evaluation,(3) sorting,(4) parameteraupdating,(5) position updating,(6) improving the initial distribution,(7) enhancing the randomness distribution,and (8) increasing the local search.The fitness evaluation needs to be calculated in combination with specific problems,so the subsequent analysis focuses on other steps.The time complexity of both initialization and position updating isO(ND),whereNis the number of individuals andDis the dimension of the objective function.The time complexity of parameteraupdating isO(1).The time complexity of sorting isO(NlogN).Among the three improved strategies in SAGWO,the amount of calculations for improving the initial distribution is very small and can be ignored.The time complexity of enhancing the randomness distribution isO(3N).In the final stage of SAGWO,the additional time spent on enhancing the local search strategy isO(0.25N).Therefore,the total complexity of SAGWO isO[T(1+N(D+logN+3.25))+ND],where the maximum number of evaluations isT.

4 FSS unit optimization model

Traditionally,the geometric size of an FSS unit structure is considered an optimization variable in a swarm intelligence algorithm.Traditional methods are simple and efficient in the FSS optimization process,but do not make full use of the searchability advantages of the intelligent optimization algorithm.In most FSS optimizations,the unit shape is limited by the traditional variable types,making it difficult to change greatly.To fully exploit the ability of SAGWO optimization,we propose a coordinated unit deformation method that uses the node coordinates of the unit structure as variables.The novel model has a larger design space,which is suitable for SAGWO global searchability.Fig.4 illustrates the eight-node FSS unit modeling method.The method consists of the following three steps:

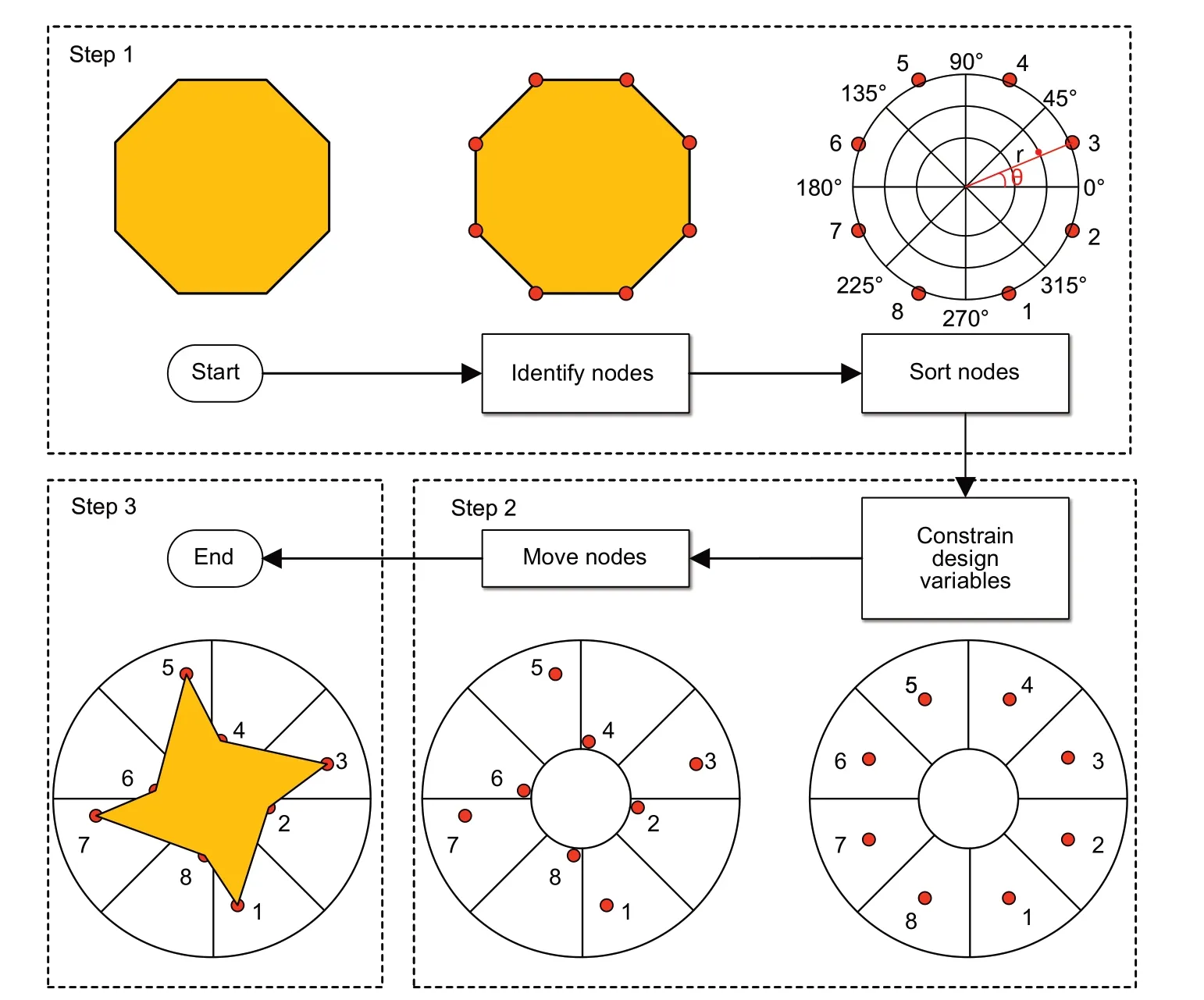
Fig.4 Illustration of the eight-node FSS unit modeling method

1.Determine the constituent unit nodes.Analyze the unit’s basic structure,mark the nodes on their outline,and number each node in counterclockwise order.Since FSS units are mostly centrally symmetrical,we establish a polar coordinate system that uses the centroid as the midpoint to record the relative position information of each node.The location of each node is determined by the azimuthθand radiusr.To parameterize the expression of the unit shape,we store all the information of the nodes in a real number array.SAGWO changes the FSS unit by changing the data in the array.The dimensionality of the optimization problem can be reduced by the symmetric relationship between nodes.

2.Change the positions of the nodes in the limited interval.When the FSS shape changes,the active area of each node must be constrained to maintain the unit’s stability.The size range of the FSS is restricted to a specific design space.After the nodal variables are constrained,the real number array of nodal information is transmitted to SAGWO.The nodal information is updated in the SAGWO iteration,and the results are turned back to the real number array.

3.Re-establish the shape of the FSS unit according to the new node coordinates.According to the nodal position information in the real number array,the new 2D graph of the units’ shape is re-plotted.Simultaneously,the information of the current nodes is transmitted to step 1 for the next iteration.

The novel FSS optimization model breaks the traditional limitation that the length of the line segment can change only in the one-dimensional space,and the shape of the unit changes in a certain area of the 2D space.

The whole FSS optimization process is shown in Fig.5.The FSS optimization model is used at the beginning to initialize the FSS parameter,and then is combined with SAGWO in the iteration process(marked in red in Fig.5).In this case,the population size is 20 and the maximum number of iterations is 50.The dimension of the optimization problem is equal to twice the number of nodes that need to be optimized.

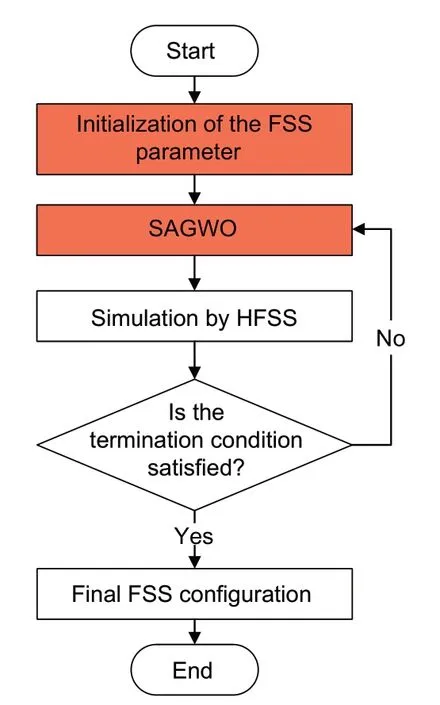
Fig.5 Flowchart of FSS unit optimization (References to color refer to the online version of this figure)

The electromagnetic simulation is performed by the commercial electromagnetic simulation software High-Frequency Structure Simulator (HFSS).After the simulation,HFSS returns the imaginary transmission coefficientS21,which is the ratio of the input power to the output power.This is used to judge the ability of FSS to transmit electromagnetic waves of various frequencies.Using our proposed method,the optimization should reduce theS21of FSS in the working frequency band.Therefore,the fitness function can be set according to Eq.(16),which transforms imaginaryS21into a real number:

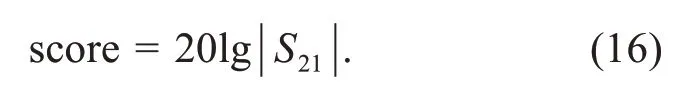
In SAGWO,the three FSS unit structures with the smallestS21values are used for leaders.

5 Numerical results

5.1 Benchmarks

Fifteen common benchmark functions were used to test the performance of SAGWO,among which formulae 1-5 are unimodal benchmark functions,formulae 6-10 are multimodal benchmark functions,and formulae 11-15 are fixed-dimension multimodal benchmark functions.Detailed expression of the 15 functions is given in Table S1,and the 2D graphic is depicted in Fig.S1.

5.2 Performance of GWO with different increased randomness strategies

We introduced three GWOs with different increased randomness strategies: Sin-GWO,Cos-GWO,and Ex-GWO.None of them include the strategy described in Section 3.3,so this test is able to reflect the difference between the three randomastrategies.Benchmark functions were used to test three algorithms (Table S1) to select an optimal one.In this subsection,the population size for each algorithm was set to 50,and the maximum number of iterations was 500.To obtain statistical results,each algorithm was independently calculated 30 times,and the average value was obtained.Tables S2-S4 show the results of these three algorithms.

According to Tables S2-S4,Ex-GWO had the lowest value in 10 benchmarks (f1,f3,f4,f5,f7,f8,f9,f13,f14,andf15),and showed the best performance.These three algorithms gave similar results for the other benchmarks.

Table 1 shows the Wilcoxon sign rank test results of these three algorithms,which can test the significance of differences.In pairwise comparisons of two algorithms,+/-indicates that the first algorithm is significantly better/worse.The ranks of mark +are recorded inR+,andR-is the sum of ranks of mark -.If there is no significant difference between the results of two algorithms,the rank is squared byR+andR-.“=” indicates no significant difference between two algorithms.The statistical significance valueαwas 0.05.Thep-value was calculated usingthe ranksum function in Matlab.Ap-value less thanαindicates a significant difference between the two groups of data.

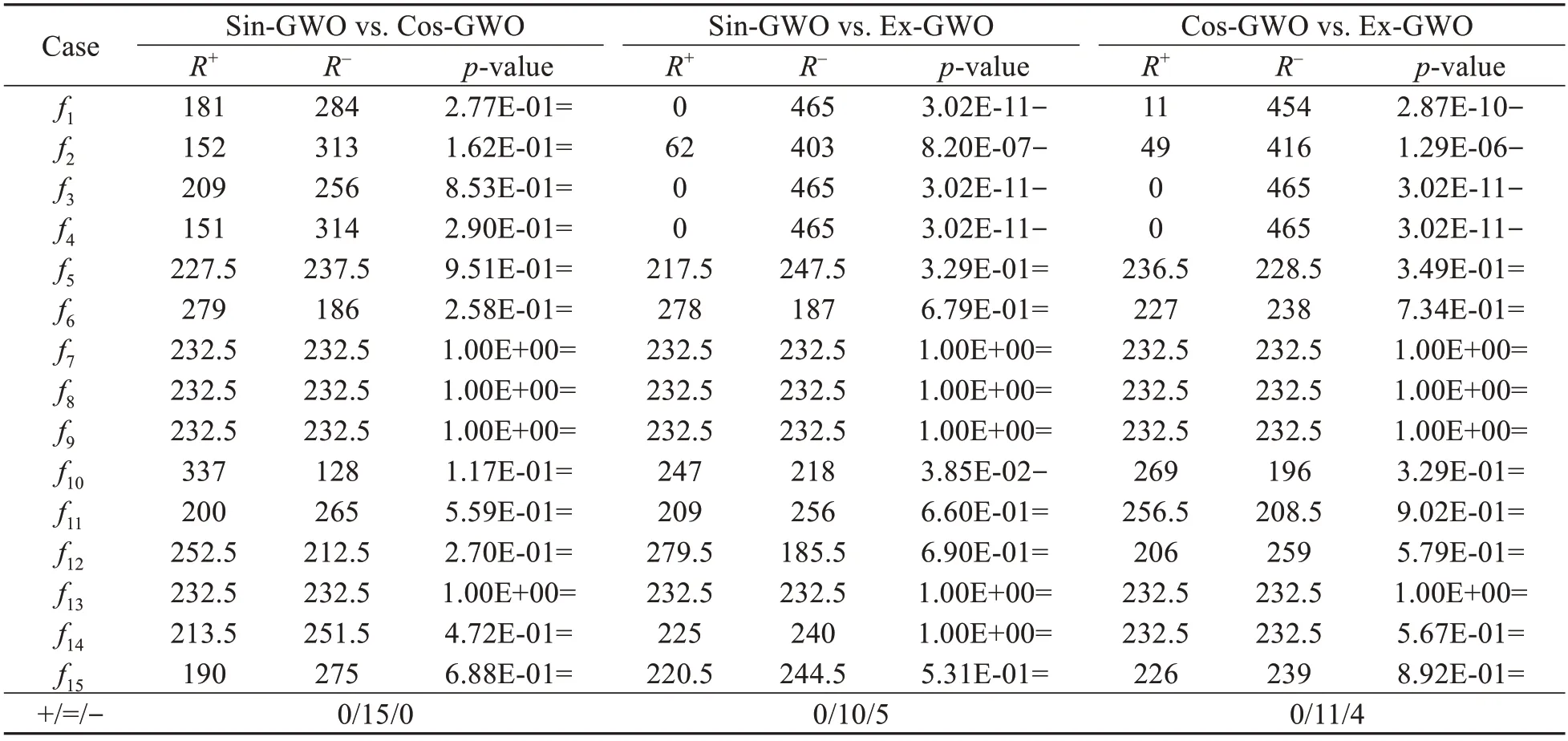
Table 1 Wilcoxon sign rank test on the solutions obtained by different algorithms for benchmarks in Tables S2-S4 (α=0.05)

After comparison analysis,three conclusions could be drawn.First,anti-study and random step size can cooperate.Different random strategies have different effects on the algorithm.Second,the effect of sin and cos is the same.Third,Ex-GWO is the clear leader in the unimodal benchmark,and the improvement of the algorithm is reflected mainly in stronger exploration.Therefore,SAGWO was built based on Ex-GWO and enhanced the local search strategy.

5.3 Comparison of the proposed algorithm with other algorithms

To study the optimization performance of SAGWO,we compared it with GWO,GA,and PSO.The test conditions were the same as in Section 5.2.The crossover rate of GA was 0.8,and the mutation rate was determined by Gaussian analysis.The calculation results of three types of benchmark functions are recorded in Tables S5-S7.

According to Table 2,SAGWO had the best statistical result in 10 of 15 tests,indicating that it was the best among the four algorithms.GWO was ranked the second,PSO third,and GA fourth.

Table S5 shows that SAGWO had advantages in most unimodal function tests,and that the standarddeviation was the smallest in multiple tests,showing high stability.This demonstrates that the proposed SAGWO has better global search ability compared to conventional GWOs.

Table 2 Numerical results of the rank of different algorithms

In the multimodal and composite function tests,the results were similar.PSO performed best inf10andf11,and GWO performed best inf14andf15.GA could not converge to the best results on any problem.Compared to the results obtained by Ex-GWO,SAGWO was better in the multimodal and composite benchmarks.The partial basic GWO assists SAGWO in achieving a better balance between exploitation and exploration.To further explore the test results,the Wilcoxon sign rank test was used to verify the significant differences among the four algorithms.In general,SAGWO showed the best optimization results(Table 3).

Furthermore,SAGWO was compared with two other improved GWOs: improved GWO (IGWO)(Nadimi-Shahraki et al.,2021) and selective oppositionbased GWO (SOGWO) (Dhargupta et al.,2020).The calculation results are recorded in Tables S8-S10.Table 4 shows the Wilcoxon sign rank test results obtained by these two improved GWOs.

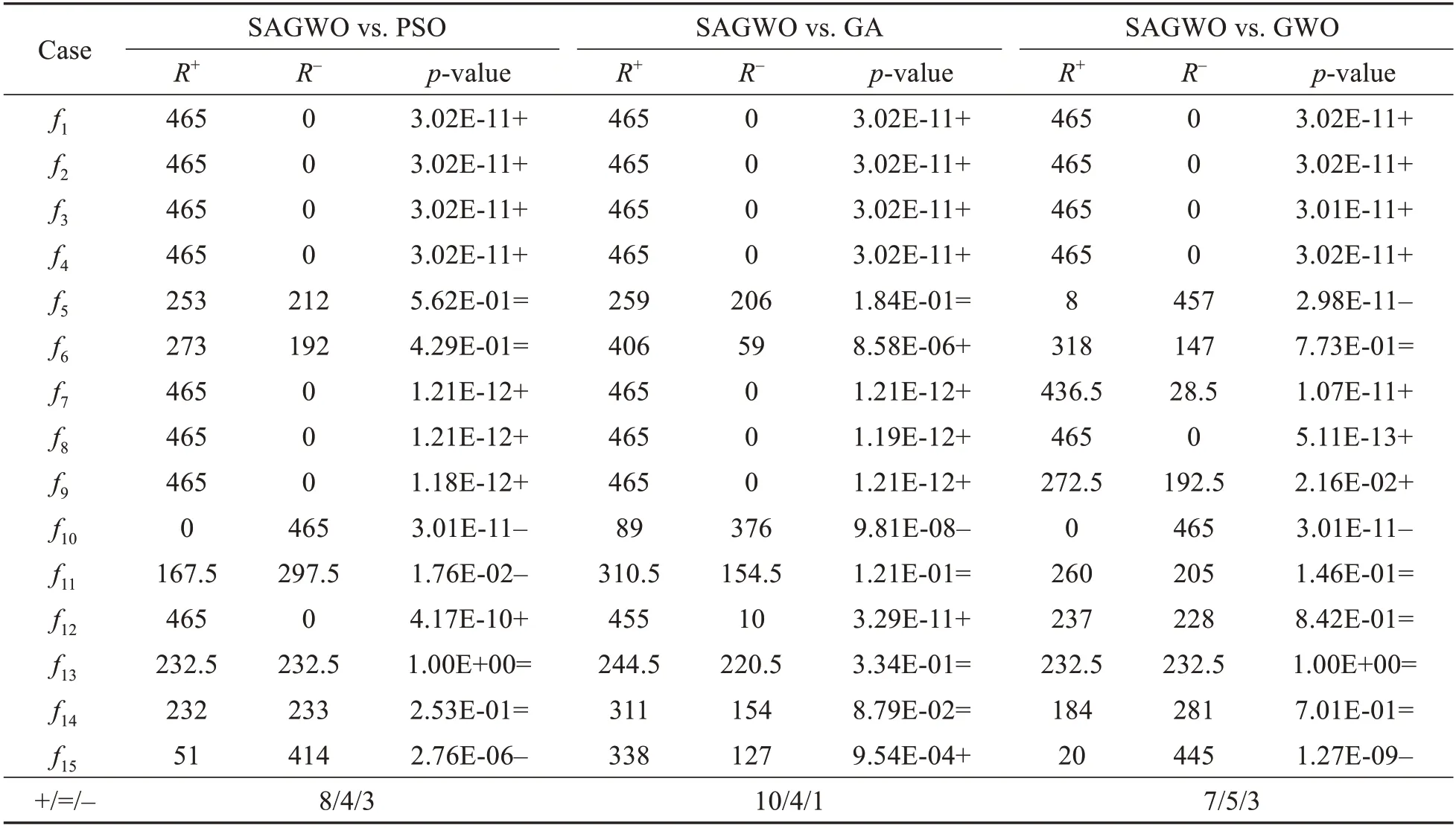
Table 3 Wilcoxon sign rank test of the solutions obtained by different algorithms for benchmarks in Tables S5-S7(α=0.05)

Table 4 shows that SAGWO had obvious advantages over IGWO and SOGWO in the unimodal function tests.Only inf5,did IGWO have slightly better results than SAGWO,but the difference was very small.In the multimodal benchmark tests,IGWO and SOGWO surpassed SAGWO inf10.SAGWO obtained the best average results fromf6tof9(Table S9).Inf14andf15,the results of SAGWO were worse than those of the two other algorithms,but the gap between these three was very small (Table S10).Compared with the recently proposed improved GWOs,SAGWO showed superior performance under most circumstances,especially for unimodal functions.

Table 4 Wilcoxon sign rank test of the solutions obtained by the two improved GWOs for benchmarks in Tables S8-S10(α=0.05)

5.4 Comparison of the convergence speeds of SAGWO and GWO

Fig.6 shows the curves of SAGWO and GWO in different benchmark optimization processes,indicating the convergence speed of these two algorithms.In the unimodal functionsf1-f5,SAGWO’s convergencespeed and optimization effect surpassed those of GWO.

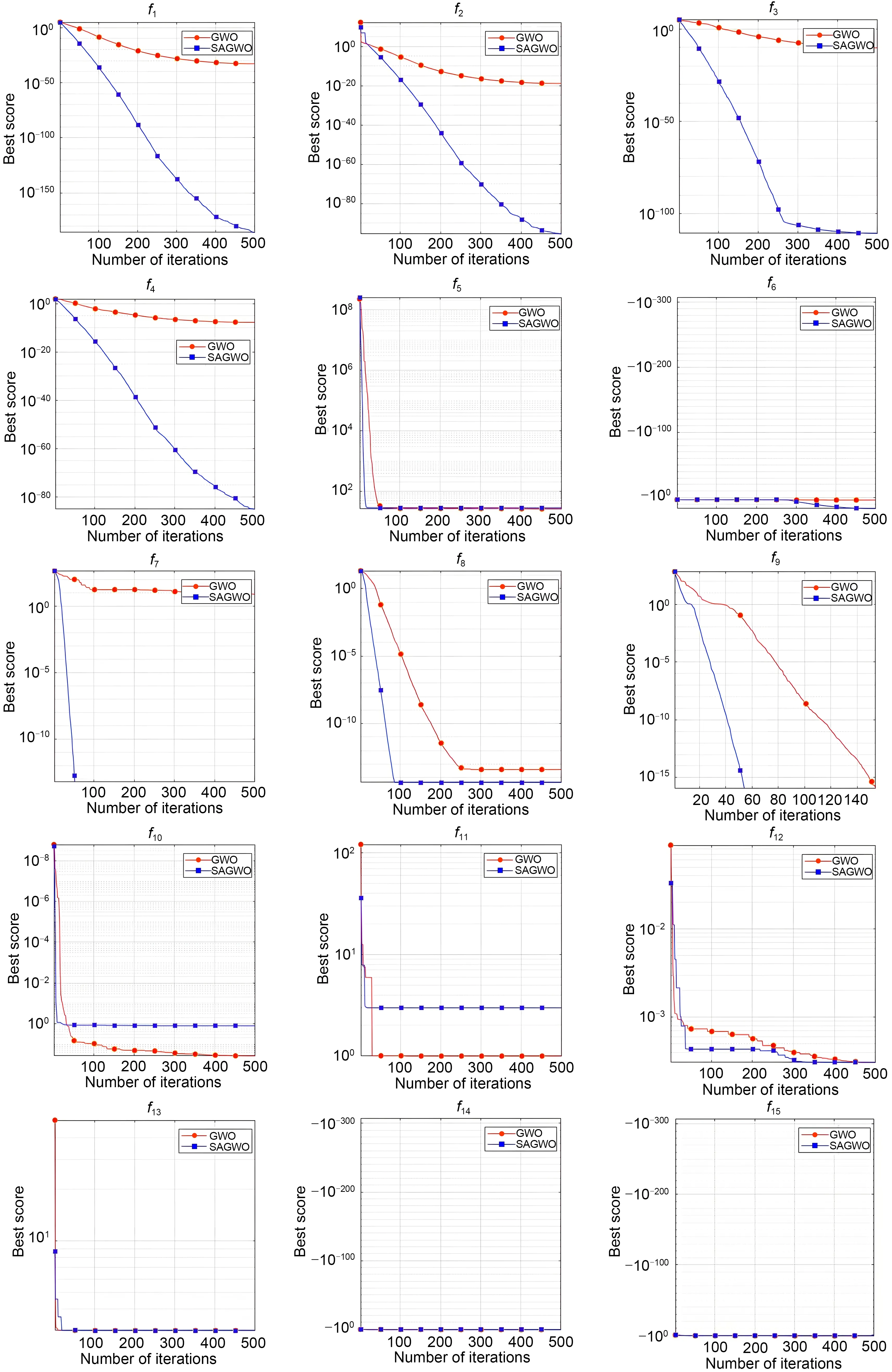
Fig.6 Convergence graph of benchmark functions

SAGWO’s result of the 100thiteration was close to the GWO’s final result (after 500 iterations).Inf6andf10,the convergence speeds of the two algorithms were very close.Inf7-f9,SAGWO had better performance.GWO surpassed SAGWO inf11andf12.Inf13-f15,these two algorithms had almost the same convergence speed.The first two proposed strategies contributed to SAGWO’s higher convergence speed.

5.5 FSS unit optimization results

In this study,we presented a double-layer hexadecanoic ring FSS.We optimized the shape of a regular hexadecanoic FSS unit to give electromagnetic shielding characteristics at 28 GHz.The shape of the unit before optimization is shown in Fig.7.The width of each side of the ring was 0.3 mm,and the width of the inner side was 1 mm from the center.The ring was copper,and the FR4 material was used as the substrate with a thickness of 1.5 mm.

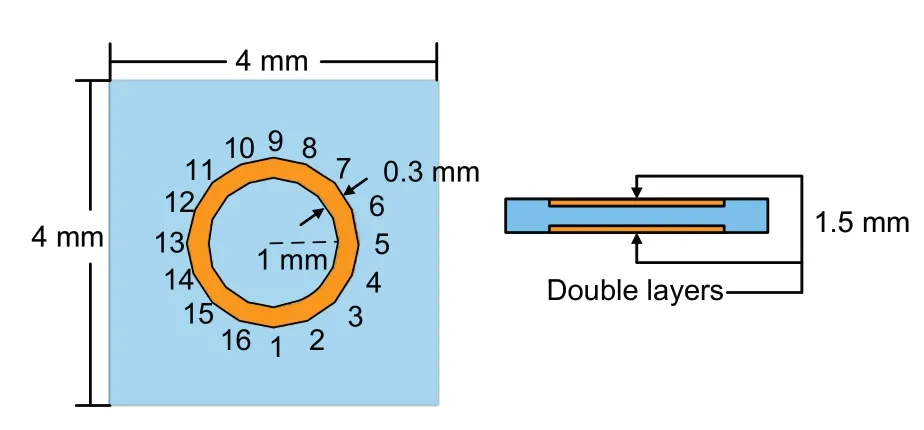
Fig.7 Design domain of ring units

According to the number of nodes,the nodes of the ring unit can be divided into 16 sectors of 22.5°.The distance between the nodes and the center should be greater than 0.5 mm and less than 1.4 mm.The width of the ring remained constant.The results obtained by SAGWO optimization are shown in Fig.8,and Table 5 shows the coordinates of nodes 1-4.Since the FSS unit was a centrally symmetrical graph,the coordinates of the remaining nodes can be obtained by adding 90°,180°,and 270° to the azimuth angle in Table 5.

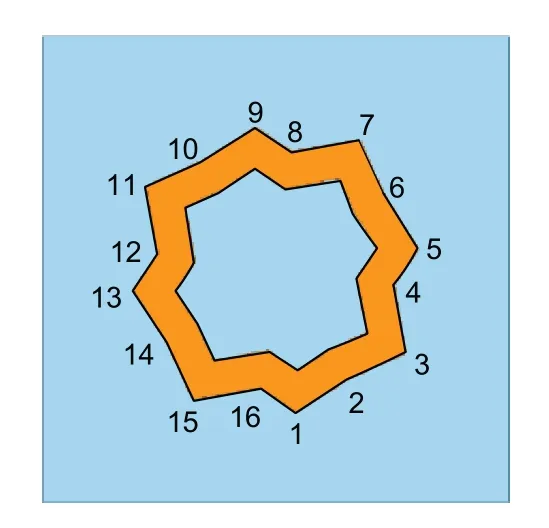
Fig.8 Shape optimization results of ring units

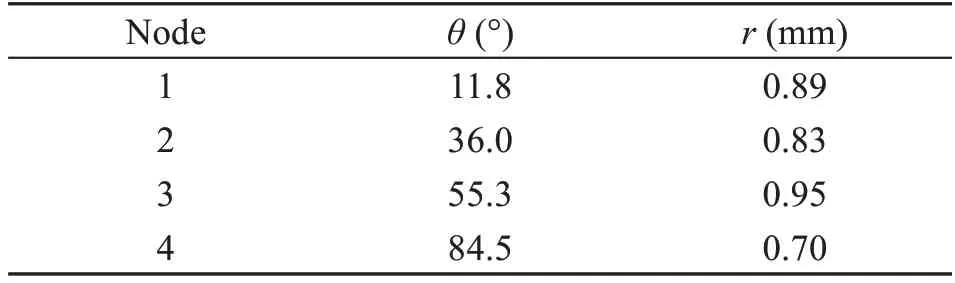
Table 5 Optimization results of ring unit nodes

The simulation results in TE mode are shown in Fig.9.The original unit had a resonance point at 25.8 GHz,andS21was -34.4 dB.S21was -18.7 dB at 28 GHz.After optimization,the resonance point moved to a high frequency.The optimized unit had a resonance point at 27.8 Hz,andS21was at least-34.2 dB.The bandwidth below -20 dB was about 2.6 GHz (26.8-29.4 GHz).The simulation results showed that the electromagnetic shielding effect of FSS near 28 GHz has been enhanced by 14.5 dB after optimization.Fig.9b shows theS21curves for different incident angles in TE mode.As the incident angle increased,the resonance point shifted only slightly.The 27.8 GHz resonance point moved to 27.4 GHz when the incident angle increased to 40°,a shift of 0.4 GHz to the low frequency.Fig.9c shows theS21curves in TM mode.The TM mode resonance point shifted to 27.2 GHz at an incident angle of 40°.With an increasing incident angle,the TM modeS21curve shifted more than the TE mode one.The TM mode resonance pointS21was -28.3 dB at 40°,where the TE modeS21was still below -30 dB.In conclusion,the optimized FSS can achieve angle stability around 28 GHz,but the TM modeS21curve fluctuated slightly.In future work,the angular stability of FSS needs further investigation.

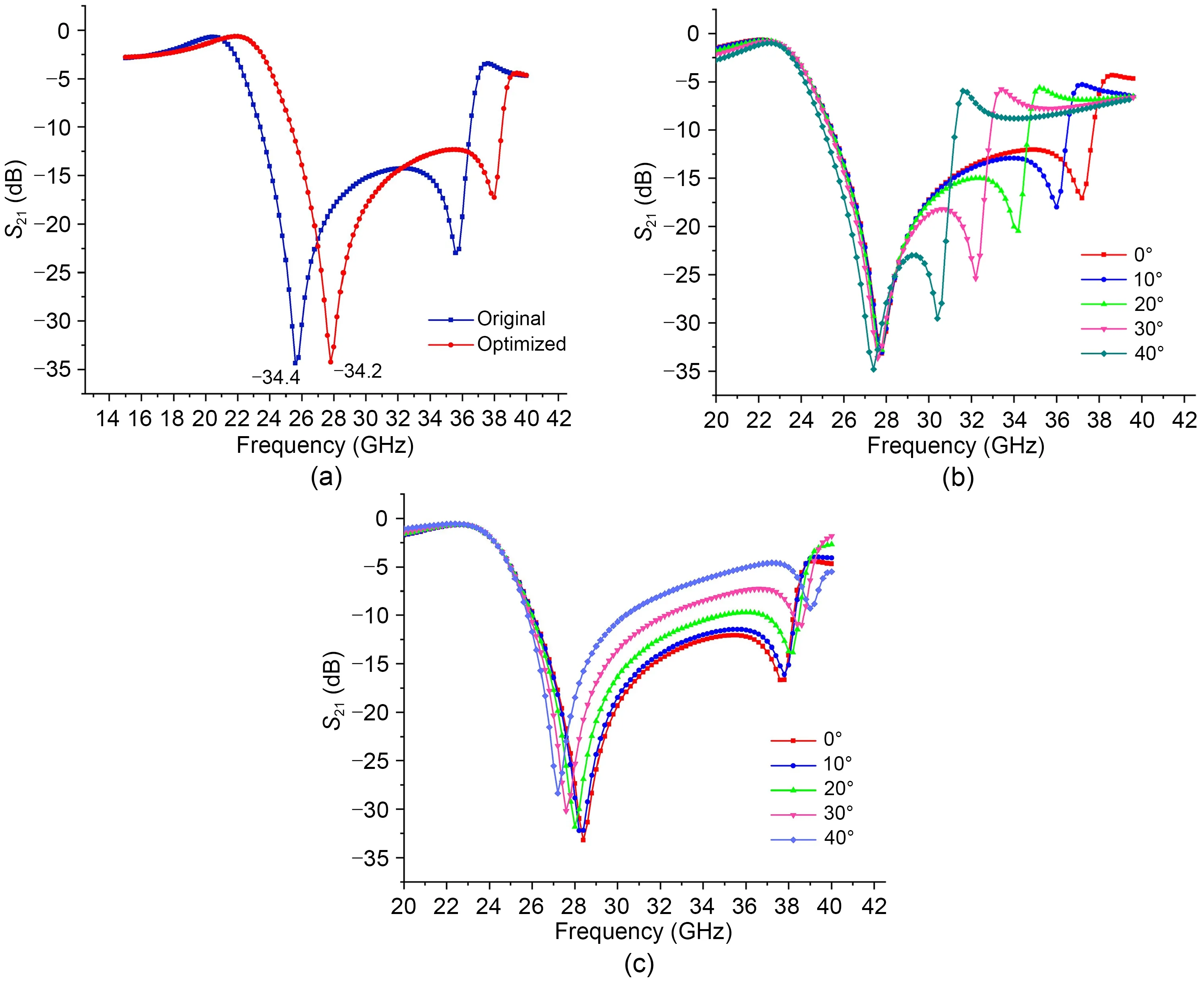
Fig.9 Simulation results S21 of the ring unit: (a) original and optimized results;(b) with different incident angles in TE mode;(c)with different incident angles in TM mode

To verify the reliability of the novel design method,a sample of the optimized FSS was fabricated and measured using the free-space method.The sample,including 50×50 units with an overall size of 20 cm×20 cm,was manufactured by the printed circuit board technology(Fig.10).

Fig.10 FSS sample

Fig.11a shows the schematic of the free-space method,and Fig.11b shows the test instruments in a microwave anechoic chamber.The main measuring instruments were the Agilent E8363B vector network analyzer and two horn antennas.

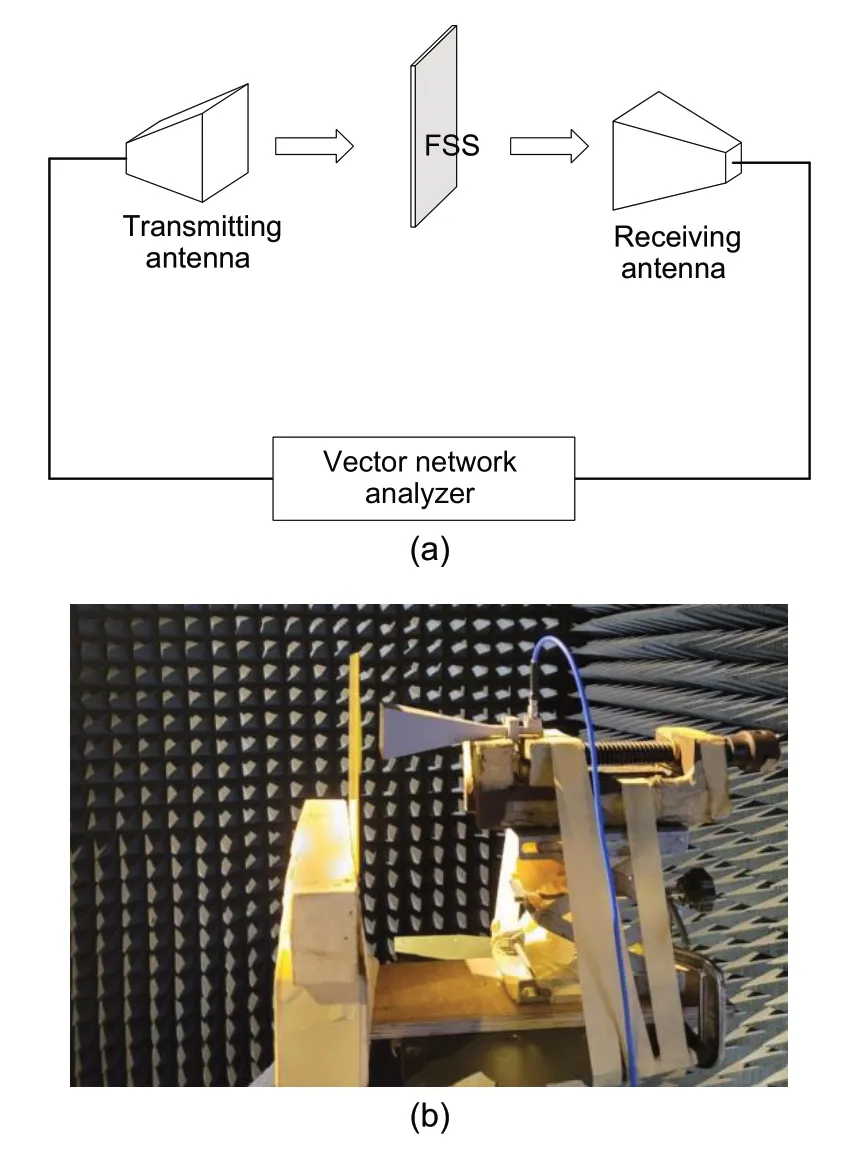
Fig.11 FSS measurement: (a) free-space method;(b) test instruments

Fig.12 shows theS21of the sample.The measured resonance point appeared at 28.6 GHz,a 0.8 GHz shift compared to the simulation result.The main reasons for this shift are the inevitable errors in manufacturing the sample and the sensitivity of the horn antenna when receiving high-frequency electromagnetic waves.However,the measured-20 dB stopband was 27.6-30 GHz,which is sufficient to meet the actual electromagnetic shielding requirements.Therefore,the measurement error is acceptable,and the test results verified the reliability and validity of the new FSS design method.

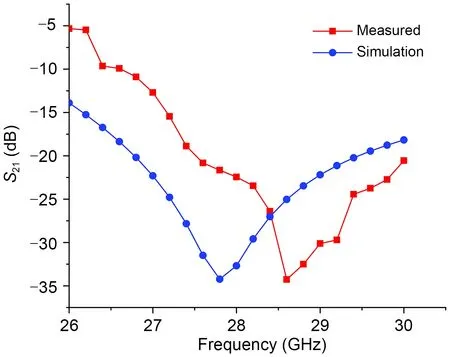
Fig.12 Measured and simulation S21 of the ring unit

6 Conclusions

In this study we proposed a novel SAGWO and applied it to the design of an 5G FSS.Before confirming SAGWO,we proposed three randomness strategies:Sin-GWO,Cos-GWO,and Ex-GWO.Ex-GWO was chosen to build SAGWO since it performed the best in 10 benchmarks.Due to three improved strategies,improving the initial distribution,increasing randomness,and enhancing local search,SAGWO obtained the best results in 10 of 15 benchmarks compared with the original GWO,GA,and PSO.Compared with IGWO and SOGWO,SAGWO had obvious advantages in the unimodal test.SAGWO converged faster than the original GWO in most tests.We also optimized a double-layer ring FSS using SAGWO with the novel FSS shape optimization method.The optimized FSS was suitable for 5G EMI shielding at 28 GHz and was verified by a free-space method test.In future work,SAGWO could be used in more fields to further evaluate its ability to solve practical engineering problems.

Contributors

Zhihao HE and Yingjun WANG designed the research,processed the data,and drafted the paper.Gang JIN helped organize the paper.Zhihao HE,Gang JIN,and Yingjun WANG revised and finalized the paper.

Compliance with ethics guidelines

Zhihao HE,Gang JIN,and Yingjun WANG declare that they have no conflict of interest.

List of supplementary materials

Fig.S1 Two-dimensional graphics of benchmark functions Table S1 Benchmark functions and their properties

Table S2 Comparison results of differentasvalues in unimodal benchmarks

Table S3 Comparison results of differentasvalues in multimodal benchmarks

Table S4 Comparison results of differentasvalues in fixeddimension multimodal benchmarks

Table S5 Comparison results of the unimodal benchmark functions

Table S6 Comparison results of the multimodal benchmark functions

Table S7 Comparison results of the fixed-dimension multimodal benchmark functions

Table S8 Comparison results of the unimodal benchmark functions of different improved grey wolf algorithms

Table S9 Comparison results of the multimodal benchmark functions of different improved grey wolf algorithms

Table S10 Comparison results of the fixed-dimension multimodal benchmarkfunctionsofdifferentimprovedgreywolfalgorithms