Competitive binary multi-objective grey wolf optimizer for fast compact antenna topology optimization＊#

Jian DONG,Xia YUAN,Meng WANG

School of Computer Science and Engineering,Central South University,Changsha 410083,China

E-mail:dongjian@csu.edu.cn;yuan0927@csu.edu.cn;mwang2@csu.edu.cn

Abstract:We propose a competitive binary multi-objective grey wolf optimizer(CBMOGWO)to reduce the heavy computational burden of conventional multi-objective antenna topology optimization problems.This method introduces a population competition mechanism to reduce the burden of electromagnetic (EM) simulation and achieve appropriate fitness values.Furthermore,we introduce a function of cosine oscillation to improve the linear convergence factor of the original binary multi-objective grey wolf optimizer (BMOGWO) to achieve a good balance between exploration and exploitation.Then,the optimization performance of CBMOGWO is verified on 12 standard multi-objective test problems (MOTPs) and four multi-objective knapsack problems(MOKPs) by comparison with the original BMOGWO and the traditional binary multi-objective particle swarm optimization(BMOPSO).Finally,the effectiveness of our method in reducing the computational cost is validated by an example of a compact high-isolation dual-band multiple-input multiple-output (MIMO) antenna with high-dimensional mixed design variables and multiple objectives.The experimental results show that CBMOGWO reduces nearly half of the computational cost compared with traditional methods,which indicates that our method is highly efficient for complex antenna topology optimization problems.It provides new ideas for exploring new and unexpected antenna structures based on multi-objective evolutionary algorithms(MOEAs)in a flexible and efficient manner.

Key words:Antenna topology optimization;Multi-objective grey wolf optimizer;High-dimensional mixed variables;Fast design

1 Introduction

In recent years,antenna design has been given considerations for multiple performance indicators simultaneously,e.g.,wideband or multiband,high gain or efficiency,and compact size (Dong et al.,2019a).Electromagnetic (EM)simulation has always been an integral part of the evaluation and optimization of antenna systems (Pietrenko-Dabrowska et al.,2020).In the traditional approaches,hundreds or even thousands of design cycles are implemented to optimize the antenna parameters of an initial antenna topology.However,this process usually relies on the designers’expertise and involves tedious work,which might not generate satisfactory results.

Antenna optimization based on evolutionary algorithms (EAs) opened a new door for antenna design because it relieves the reliance on antenna design experience.Multi-objective EAs have been successfully applied to antenna design,such as the genetic algorithm (GA) (Panduro et al.,2005;Lin et al.,2012;Chirikov et al.,2013),particle swarm optimization (PSO) (Li YL et al.,2013;Gupta et al.,2020),the differential evolution (DE) algorithm (Chen and Wang,2012;Li R et al.,2017;Kaur et al.,2019),the non-dominated sorting genetic algorithm (NSGA)(Kim and Walton,2006;Panduro et al.,2013;Bin et al.,2020),and the multi-objective evolutionary algorithm based on decomposition(MOEA/D)(Carvalho et al.,2012;Li QQ et al.,2020a).Among these optimization methods,some transform multiple optimization goals into an objective function in particular ways,while others adopt the multi-objective version of intelligent optimization algorithms.However,the abovementioned antenna optimization methods based on continuous EAs require a particular antenna shape as a starting point,and then search for and optimize part of the antenna sizes within a given range,which poses the challenge of relying on the knowledge of antenna designers and also limits the diversity of antenna geometries.

Due to the limitation of antenna optimization designs based on continuous EAs,automatic antenna topology optimization based on binary EAs has been developed to optimize the antenna topology.Topology optimization,also known as pixel optimization,discretizes the design space into small pixels represented by a matrix with “1” (conductor) and “0” (air).Zhang L et al.(2019) designed antenna topology for maximum bandwidth combining GA with the method of moments.Dong et al.(2018)proposed an improved binary particle swarm optimization (BPSO) algorithm to acquire a high-dimensional,multifunctional,and compact fragment-type antenna.Jia and Lu (2019)applied a hybrid Taguchi BPSO to EM optimization problems.Zhu et al.(2019) used a hybrid topology optimization method to realize the isolation structure of a multiple-input multiple-output (MIMO) antenna.Li QQ et al.(2020b) integrated PSO and MOEA/D to design a compact high-isolation MIMO antenna.A multi-objective evolutionary algorithm based on decomposition combined with enhanced genetic operators (MOEA/D-GO) was used to design an ultrawideband planar antenna (Du et al.,2020).The above methods based on binary EAs no longer restrict the initial antenna structure.However,they also face the challenge that the EM simulation cost tremendously increases with the number of iterations and populations in EAs.Therefore,the problem of high computational cost remains.

The combination of neural network and antenna design reduces the computational burden of antenna optimization design to a certain extent.However,there is a non-negligible computational cost to obtain the training and test datasets of the neural network.In antenna design,the cost of acquiring training datasets through physical testing or EM simulation software is very high.Moreover,the size of the dataset of the training neural network is often related to the antenna variables to be optimized,and the more variables there are,the larger dataset is needed (Bataineh and Marler,2017;Li CM et al.,2020).To optimize 10 antenna variables,Dong et al.(2019b) obtained 190 sets of training data and 10 sets of testing data to train and test the back propagation neural network(BPNN).Our research team collected 220 sets of data to train and test the radial basis function neural network (RBFNN) to optimize 10 design variables for the antenna(Dong et al.,2019a).Dhaliwal and Pattnaik(2017) used 40 sets of data to train artifical neural network (ANN) to optimize two design variables for a compact fractal antenna.Pietrenko-Dabrowska et al.(2020)found that 400 sets of training data were appropriate for training Kriging surrogates to optimize a triple band uniplanar dipole antenna and a quasi-Yagi antenna with 10 design variables.The abovementioned antenna design types based on neural networks all belong to the size design with continuous design variables,and the number of antenna variables to be optimized is always around 10.In antenna topology optimization,there are usually tens or even hundreds of design variables,and the number of training sets will also increase greatly,which requires a huge computational cost.Therefore,it is currently not feasible to train neural networks with tens and hundreds of datasets for antenna topology optimization.

In this work,a competitive binary multi-objective grey wolf optimizer (CBMOGWO) for improving the efficiency of antenna optimization is proposed to pose the challenges of high-dimensional mixed variables and multiple objectives.The multi-objective grey wolf optimizer (MOGWO) (Mirjalili et al.,2016)shows superior search performance compared with the classic multi-objective particle swarm algorithm(MOPSO) (Coello et al.,2004) and MOEA/D (Zhang QF and Li,2007) due to its social leadership and hunting technology.Based on MOGWO,the contributions of this work are given below: (1) introducing the competition mechanism to divide the population into several parts,so as to reduce the difficulty of calculation (Aldhafeeri and Rahmat-Samii,2019);(2) replacing the linear convergence factor with the cosine oscillation convergence factor to achieve a better balance between exploration and exploitation;(3) designing a compact high-isolation dual-band MIMO antenna topology with high-dimensional mixed variables.In our example,CBMOGWO obtains the Pareto solution sets with only half the time of the original BMOGWO and BMOPSO,which indicates that the proposed CBMOGWO method not only has good optimization performance but also greatly improves the design efficiency.

2 Background

2.1 Problem formulation of multi-objective antenna topology optimization

Antenna is a converter between EM waves propagating in free space and guided waves propagating on a transmission line.Due to different application scenarios,the types and shapes of antennas are highly diverse.However,any antenna can be topologically optimized to obtain satisfactory antenna performance.Take a planar monopole antenna as an example.Figs.1a and 1c show the antenna before and after topology optimization,respectively.In the multiobjective antenna topology optimization process,the design vectorxis formed by the material of all pixels of the antenna patch.The constraint is thatxis a vector of 0 and 1 in the binary code.Binary code “0”means that the material is non-conductive (like air),and binary code “1” means that the material is a conductor,as shown in Fig.1b.The objective functionfk(x)(k=1,2,...,K)is usually a function related to antenna performance indicators such as return loss,gain,and isolation (Balanis,2016).In general,the problem of multi-objective antenna topology optimization is formulated as follows:

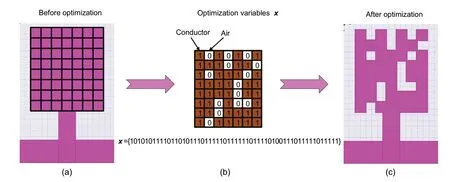
Fig.1 Diagram of antenna topology optimization: (a) antenna structure before optimization;(b) mapping between the physical antenna structure and binary vector x;(c)antenna structure after optimization

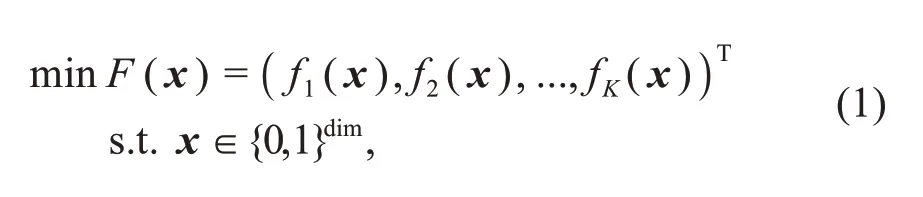
where dim represents the dimension of the optimization problem.The goal of multi-objective antenna topology optimization is to achieve non-dominated solutions,which is also known as the Pareto front(Koziel and Ogurtsov,2013;Koziel and Bekasiewicz,2016).In other words,multi-objective antenna topology optimization aims to find a trade-off among the performance indicators of the antenna without knowledge of the detailed structure of the antenna.

2.2 MOGWO and binary MOGWO

The powerful optimization ability of the grey wolf optimizer (GWO) (Mirjalili et al.,2014b) promotes the development of MOGWO to solve multi-objective problems (MOPs).The details of GWO are described in Section 1 of the supplementary materials.In MOGWO,the social hierarchy components of a grey wolf population are still the three leaders(alpha(α),beta(β),and delta (δ) wolves) and the candidate solutions (omega(ω) wolf).Note that the social leadership relationship of MOGWO is different from that of GWO in that there is no dominant relationship among its three leaders.

The hunting process of the MOGWO algorithm is the same as that of GWO.The following formulae are the same as Eqs.(S5)-(S7) in the supplementary material for the mathematical modeling of prey hunted by grey wolves in MOGWOs:

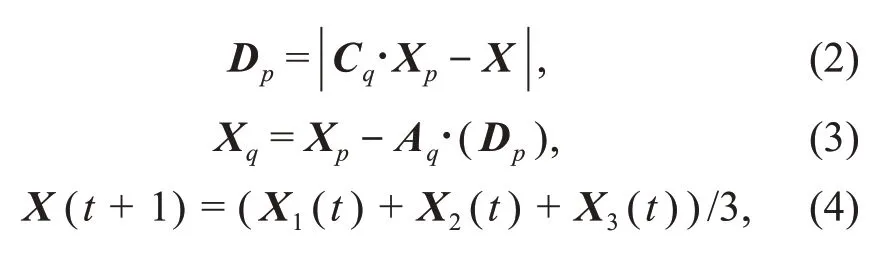
where (p,q) ∈{(α,1),(β,2),(δ,3)},tis the current iteration,Xpis the position vector of the prey,Xindicates the position vector of a grey wolf,andAandCare coefficient vectors,calculated as follows:

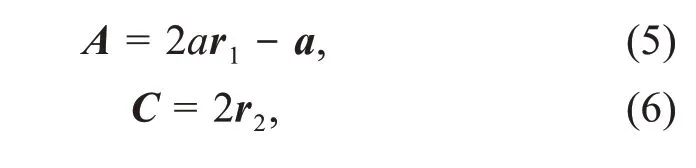
wherer1andr2are random vectors in [0,1],and the convergence factora=2-2t/T,linearly decreasing from 2 to 0 throughout the iterations.Ais an important parameter that affects the exploration and exploitation of algorithms.The candidate solutions tend to diverge from the prey when |A|＞1,and converge towards the prey when|A|＜1.Details onAcan be found in the description of GWO in supplementary materials (the roles ofAin MOGWO and GWO are exactly the same).

MOGWO adopts two important components that are very similar to those in MOPSO (Coello et al.,2004),the archive and the leader selection strategy,which are described in detail in the supplementary materials.MOGWO is designed to solve the MOP of continuous space as the grey wolf continuously moves to any point in the search space.When MOGWO is applied to antenna topology optimization,the solution vectors can be restricted to binary values.Then,the continuous MOGWO evolves to BMOGWO.This mapping relation refers to the method proposed by Emary et al.(2016).In this approach,the updated grey wolf position vector is forced to be binary,described mathematically below:

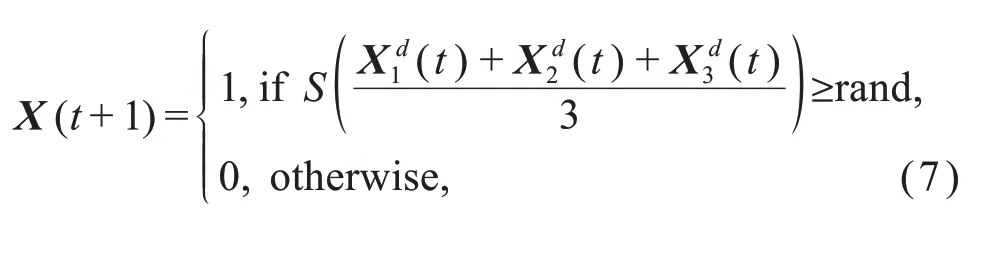
where rand represents a random number in [0,1],drepresents thedthdimension ofX,andS(·) denotes the sigmoid function,whose mathematical expression is as follows:

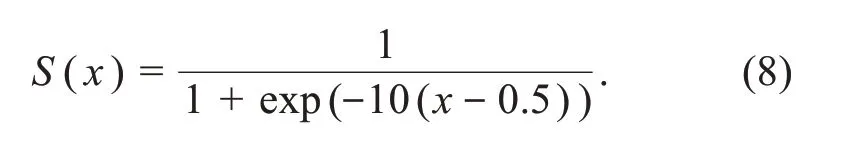
3 Competitive binary MOGWO

In antenna optimization,the number of calculations of the fitness value is equivalent to the number of EM simulations.They both increase proportionally with the population size and the number of iterations,resulting in high computational cost.To overcome this difficulty,we apply the idea of competition to BMOGWO to reduce the number of EM simulations.Then,the convergence factors are changed from linear to cosine oscillations to achieve a better balance between exploration and exploitation than the original BMOGWO.

3.1 Population competition

In this subsection,a competition mechanism is proposed to reduce the computational cost,and its general concept and idea of competition to CBMOGWO are illustrated in Fig.2.The mechanism has two main components:population division and population position update.In this competition mechanism,the population size isN.Grey wolves are randomly selected to compete in pairsxi,xj∈X(i,j=1,2,…,N,i≠j),and each grey wolf participates in the competition only once.

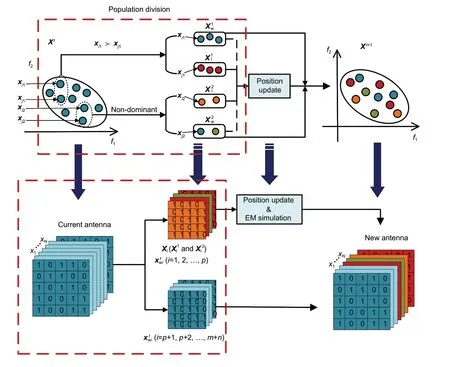
Fig.2 Competition mechanism and its application to antenna topology optimization

The application of the competition mechanism to antenna topology optimization is depicted in the lower part of Fig.2.We can observe that one part of the current antenna topologies needs to perform position update and EM simulation calculation using the competition mechanism.The other part of the antenna does not need to be updated;thereby,much time originally used for EM simulation can be saved.It is reasonable that our proposed CBMOGWO can reduce considerable computational cost due to the existence of the competitive mechanism.

3.2 Convergence factor of cosine oscillation

In the competition mechanism,not all grey wolves are updated in each iteration,which greatly reduces the diversity of the population.Otherwise,the balance of exploration and exploitation will need to be improved.A detailed analysis of the development and exploration in MOGWO can be found in Section 2 of the supplementary materials.

Improvement of convergence factora: We make up for the above shortcomings by improving the convergence factor (a) of(i=1,2,…,p).We improveathat decreases linearly with the number of iterations to cosine oscillation in this population.(i=1,2,…,p) are affected by the improved convergence factor of cosine oscillation,so they hunt in a way different fromXl,and their position changes are more random,which increases the diversity of the population to a certain extent.The improved convergence factor is calledanew,and its mathematical formula is as follows:

where rand represents a random number in [0,1].Accordingly,wheni=1,2,…,p,ai=anew;wheni=p+1,p+2,…,N,ai=a.The comparison ofabefore and after the improvement(aandanew)is shown in Fig.3.We can see that,whent＜2/T,anew＜aleads toAnew＜A,bringing the expected weaker exploration capability compared toXl.Whent≥2/T,the cosine oscillation ofanewabove and belowasometimes makesAnew＞Ato avoid the local search being too concentrated,whereAnewcorresponds toanew.Therefore,the updating of(i=1,2,…,p) withanewcould balance the exploration intensity,different froms strong exploration at the initial stage of iteration.At the later stage of iteration,anewmakes the local search intensity of the population more reasonable compared with the fixed reduction ofa,and it helps explore more areas where possible solutions exist.

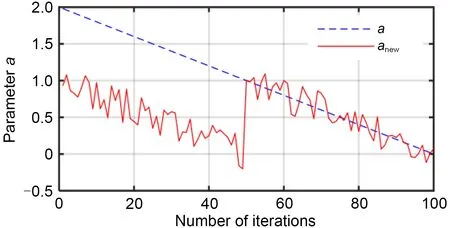
Fig.3 Convergence factors before and after improvement

The basic framework of CBMOGWO is shown in Procedure 1 in the supplementary materials.It is expected that the method proposed in this paper can not only improve the optimization performance of BMOGWO but also significantly reduce the calculation cost of antenna optimization design.

4 Numerical experiments

In this section,our proposed CBMOGWO is compared with two well-known algorithms,BMOPSO and the original BMOGWO.

4.1 Experimental setup

For BMOPSO,the following initial parameters are chosen:

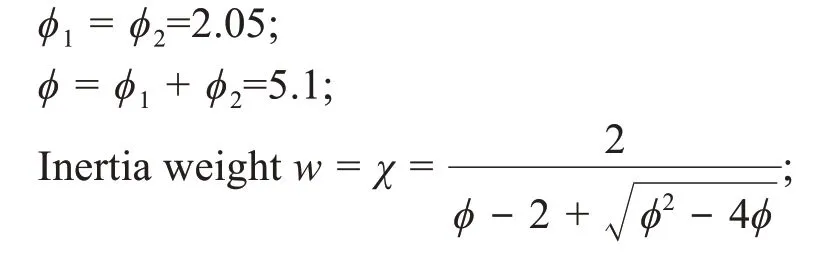
Personal coefficientC1=χ×φ1;

Social coefficientC2=χ×φ2.

For common parameters in the three algorithms,the following initial parameters are chosen:

Grid inflation parameterα=0.1;

Leader selection pressure parameterβ=4;

Number of grids per each dimension:10.

To evaluate the performance of CBMOGWO,12 standard multi-objective test problems (MOTPs)proposed in CEC2009 (Zhang QF et al.,2009)were selected,ranging from UF1 to UF12,including seven bi-objective test problems,three tri-objective test problems,and two five-objective test problems.These are shown in Tables S1-S3 in the supplementary materials.The above 12 test problems are all continuous test problems,and thus 15 bits were used to represent each continuous variable in binary form(Mirjalili et al.,2014a;Zhang QF et al.,2009).Therefore,the dimensions of grey wolves are calculated as follows:

where Dimgreywolfindicates the dimension of each grey wolf in CBMOGWO,and Dimfunctionis the dimension of a particular test problem.The population size and the maximum number of iterations were both set to 100,and the dimension of the design variable was set to 10;in other words,the grey wolves’ dimension was 150 (10×150).Furthermore,we evaluated the performance of the proposed algorithm for the multiobjective knapsack problems(MOKPs).The test problems of MOKPs were provided on the evolutionary multi-objective optimization platform PlatEMO (Tian et al.,2017).A binary MOKP withmknapsacks anddcandidate items can be described as

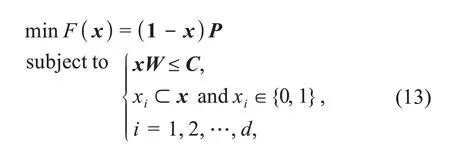
wherex=(x1,x2…,xd) represents a scheme.Ifxi=1,theithitem is selected in schemex;otherwise,it is unselected.F(x) is anm-dimensional vector that records the total profit of unselected items in each knapsack.PandWrepresent the profit and weight matrices ofditems in each knapsack,respectively.Cis the maximum capacity vector ofmknapsacks.Since the variable dimension of our designed antenna was not too high,we conducted only MOKP experiments with 250 items (i.e.,d=250).Regarding the number of targets,the performance of the proposed CBMOGWO on MOKPs with 2,3,4,and 5 targets was evaluated(i.e.,M=2,3,4,5).

The value ofΘalso affects the performance of the proposed algorithm.IfΘis too small,there will be fewer updated individuals,and the algorithm’s optimization ability will be poor.IfΘis too large,the computational cost will be greatly increased,especially of the antenna design problem.Θis set to balance the likelihood of updates toand,thus helping balance the exploration and exploitation of the algorithm.Sinceandare generated in different ways (is generated by the dominance relationship,whereasX2w is randomly generated),to make the algorithm more efficient,as manyas possible should be updated,butshould not be updated at all.We find that settingΘ=0.1 maintained the probability ofandupdates in a good dynamic balance.Note thatgives priority to update,and whenis less than 10% of the total population,will make up the difference.

To quantitatively compare the performance of each algorithm,the inverted generational distance(IGD) (Ishibuchi et al.,2015) and hypervolume (HV)(Zitzler and Thiele,1999) were selected to evaluate the convergence and diversity of the algorithm.The first metric,IGD,was proposed,and its calculation formula is as follows:

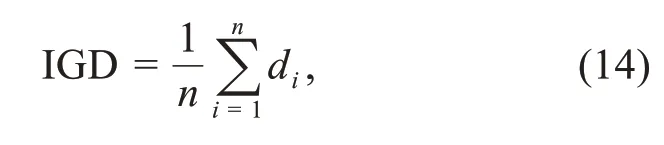
wherenrepresents the number of points in the true Pareto front.The true Pareto fronts of the standard MOTPs are obtained by Zhang QF et al.(2009)through mathematical derivation and extensive experiments.In some engineering problems there is no true Pareto front,such as MOKPs and antenna design.The parameterdiis the distance between theithpoint on the true Pareto front and the closest point in the obtained Pareto solution set,calculated using the Euclidean distance formula.Although the Euclidean distance calculation method is used,diis essentially different from the Euclidean distance because the objective function does not have the dimension of distance.Furthermore,IGD is flawed as a metric when the dimensions of multiple objective functions are not exactly the same (unless the objective functions are converted to dimensionless ones) (Marler and Arora,2004,2009).Regarding the metric of IGD,the smaller the IGD value,the better the comprehensive performance of the algorithm.Since some engineering problems do not have a true Pareto front,IGD cannot be used to evaluate the performance of the algorithm.HV is a test metric that can evaluate the performance of the algorithm in this case,and the mathematical description of HV is as follows:

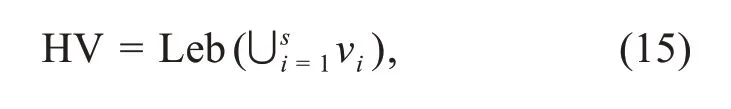
where Leb stands for the Lebesgue measure and is used to measure the volume,srepresents the number of Pareto solutions obtained,virepresents the HV formed by the reference point and theithsolution in the solution set.In the numerical experiment,since the true Pareto fronts of the 12 test problems all exist,the reference point we chose is the true non-dominated solution set.The larger the HV value,the better the convergence,uniformity,and universality of the algorithm.

4.2 Discussion of results on MOTPs

Fig.4 shows the distributions of the Pareto optimal solutions obtained by BMOPSO,BMOGWO,and CBMOGWO on the bi-and tri-objective test problems in the objective function space.The Pareto optimal solution obtained by CBMOGWO was closest to the true Pareto front.Therefore,CBMOGWO had better optimization performance according to the solution set distribution.All algorithms were run independently 30 times on each test problem,and the statistical results of IGD for these 30 trials are provided in Table S4 in the supplementary materials.The number of objectives considered in the corresponding test is shown in parentheses.It can be observed from Table S4 that CBMOGWO had lower average IGD values than the original BMOGWO and traditional BMOPSO for all instances.Meanwhile,CBMOGWO provided the best IGD values except for UF2,UF5,and UF11.Even for the worst IGD measurements of non-dominated solutions,CBMOGWO outperformed the two other algorithms.In terms of the median IGD value,CBMOGWO still provided the best non-dominated solution for all the test problems.According to the statistical results of the standard deviation,CBMOGWO yielded the smallest IGD variance,which verified the stability of its optimization performance.The significance of the above results is also illustrated in Fig.S1 in the supplementary materials.The boxplots of CBMOGWO were lower than that those of BMOGWO and BMOPSO for all test problems,and narrower than those of BMOGWO except for UF7 and UF11.IGD is a valuable metric to test the overall performance of the algorithm.Through the above analysis of the statistical results of IGD values,it can be concluded that CBMOGWO has better convergence and diversity.Fig.S2 in the supplementary materials presents the evolution curves of the average IGD value for each algorithm at each test instance.These results indicated that CBMOGWO was better than BMOGWO and far superior to BMOPSO in all instances.For most of the test problems,CBMOGWO converged the fastest,which is meaningful in dealing with complex engineering problems,such as antenna topology optimization.

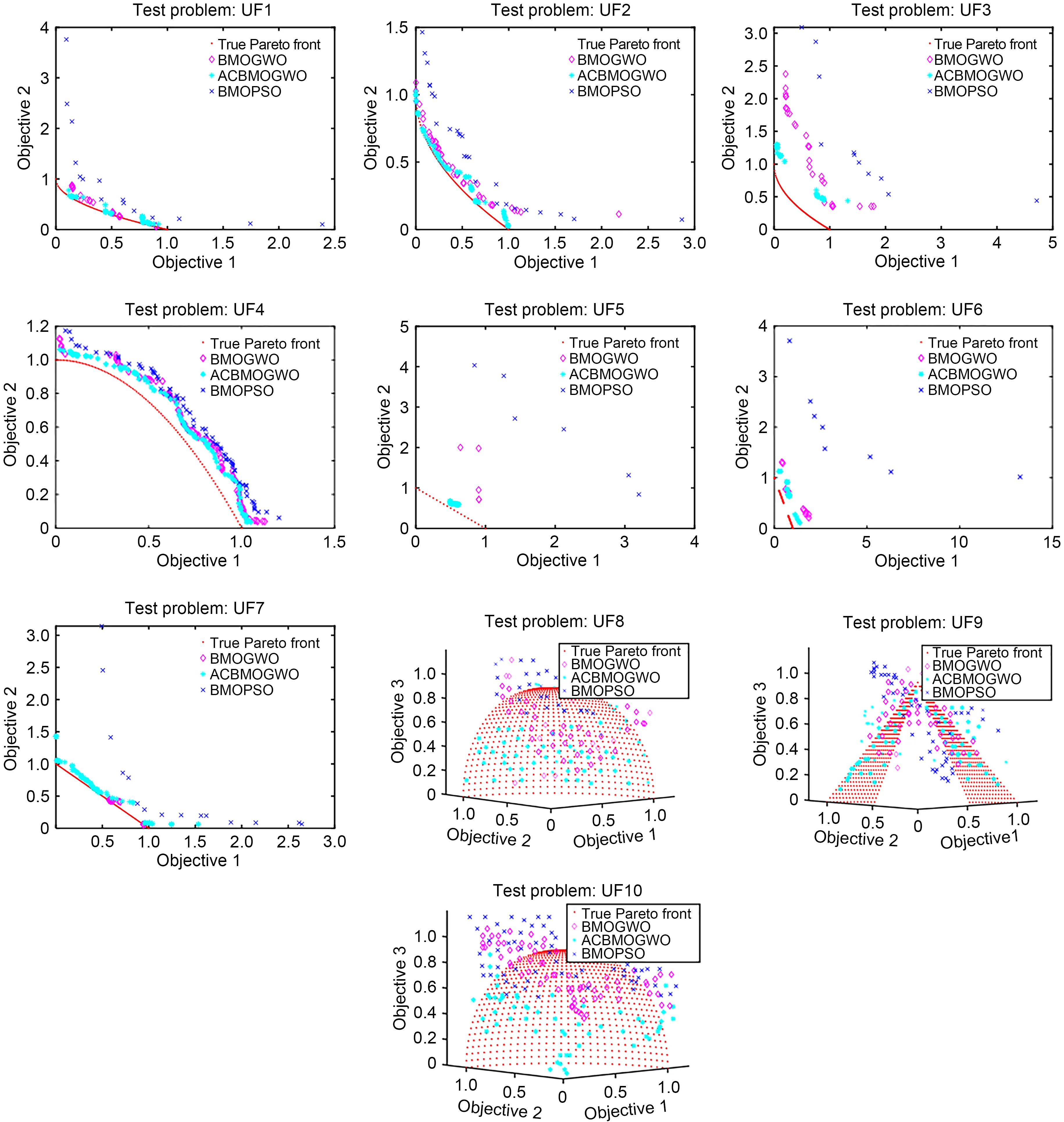
Fig.4 Obtained Pareto optimal solutions by BMOPSO,BMOGWO,and CBMOGWO for UF1 to UF10

The statistical results of HV values for another metric to MOP are shown in Table S5 in the supplementary materials.In all instances,CBMOGWO provided the largest average HV value.With the exception of UF10,CBMOGWO obtained the non-dominated solution with the best HV value.From the statistical results of the worst HV value,CBMOGWO was highly advantageous over BMOPSO,and CBMOGWO was also superior to the original BMOGWO,except for UF1,UF3,UF8,and UF9.As for the non-dominated solution with a median HV value,it can be observed that CBMOGWO provided a larger HV value except for UF9.Regarding the standard deviation of HV values,the solution set obtained by CBMOGWO was more stable than those obtained by the original BMOGWO and traditional BMOPSO,except for UF1,UF7,UF10,and UF11.Fig.S3 in the supplementary materials describes the significance of the above statistical variables from another perspective.The boxplots of CBMOGWO were higher than those of BMOGWO and BMOPSO in all instances and narrower than those of BMOGWO except for UF3 and UF11.The larger the HV value,the better the convergence,uniformity,and diversity of the algorithm.Therefore,it can be stated that CBMOGWO has stronger optimization ability in dealing with MOP.Fig.S4 in the supplementary materials presents the evolution curves of the average HV value for each algorithm for 12 test problems.It is obvious that CBMOGWO not only converged faster but also achieved a larger HV value,which shows that CBMOGWO has achieved a good balance between exploration and exploitation.

In addition,it is known that CBMOGWO updates only about half of the population in each iteration due to the characteristics of the competition mechanism.However,through the above statistical analysis of the two metrics including IGD and HV,it can still obtain better optimization capability than the original BMOGWO and is far superior to the traditional BMOPSO.Therefore,it can be concluded that our proposed CBMOGWO has robust optimization performance.

4.3 Discussion of results on MOKPs

Furthermore,we conducted a series of tests on binary MOKPs to eliminate the effect of rewriting continuous variables in binary form.Fig.5 shows the Pareto optimal solutions obtained by BMOPSO,BMOGWO,and CBMOGWO on the bi-and tri-objective MOKPs.MOKPs are minimization problems,so the closer the obtained Pareto optimization solution to the negative direction of each coordinate axis,the better the optimization performance of the corresponding algorithm.From the comparison of Pareto optimization solutions obtained by different algorithms in Fig.5,the solution set obtained by CBMOGWO was closer to the negative direction of each coordinate axis than the two other.In addition,we performed quantitative statistical analysis.Since there is no true Pareto front for MOKPs,the IGD value cannot be obtained to evaluate different algorithms.Therefore,this problem can be evaluated using only the HV value.From the statistical results on the MOKP problem in Table S6 in the supplementary materials,the HV values (average,best,and worst)of the Pareto solution set obtained by CBMOGWO were larger.In terms of the standard deviation,although the standard deviation of the CBMOGWO was not always the smallest,it was still within an acceptable range.Fig.S5 in the supplementary materials depicts the degree of dispersion of the HV values.First,it can be observed that the boxplot of the HV value obtained by CBMOGWO was higher,which indicates that the Pareto solution set obtained by this algorithm more uniform and diverse.Second,the boxplot obtained by CBMOGWO was much narrower than that of BMOGWO in MOKP withM=3,and close to that of BMOGWO for other instances,which shows that CBMOGWO has stable optimization ability.Fig.S6 in the supplementary materials presents the evolution of the HV value with the number of iterations on MOKPs.The HV value of the Pareto solution set obtained by CBMOGWO was always significantly higher than those of the two other algorithms in the evolution process.From the above discussion,it can be concluded that our proposed CBMOGWO performs better than the original BMOGWO and the classic BMOPSO.

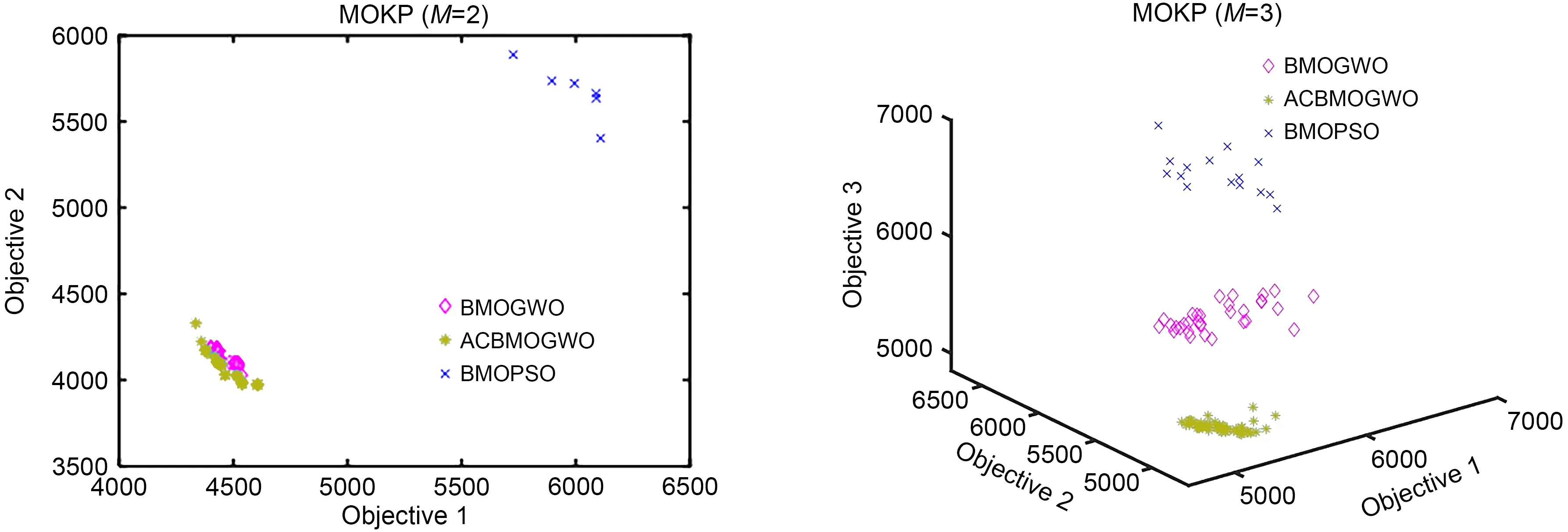
Fig.5 Pareto optimal solutions obtained by BMOPSO,BMOGWO,and CBMOGWO for MOKPs

5 Compact high-isolation dual-band MIMO antenna design with high-dimensional mixed variables

The high efficiency of the proposed CBMOGWO in antenna topology optimization was verified by a design example of MIMO antenna.With the development of wireless terminal equipment,the space for placing the antenna is becoming gradually smaller,and the antenna structure is getting more compact.In the miniaturized MIMO antenna,the coupling between the antennas becomes stronger due to the more compact antenna structure.These coupled energies can greatly affect the radiation performance of the antenna;therefore,compact MIMO antennas with high isolation are in high demand in current fifth-generation technology,as well as in the forthcoming sixth-generation wireless communication systems(Jehangir and Sharawi,2020).In general,in the conventional antenna optimization design using EAs,there is usually only one type of optimization,either size optimization with continuous variables or topology optimization with binary variables.Moreover,automatic multi-objective antenna designs usually deal with only two optimization objectives(Dong et al.,2019a,2019b).In our MIMO antenna design,we used CBMOGWO to optimize both the continuous design variables and the binary design variables with highly variable dimensions and multiple optimization objectives.

The initial MIMO antenna model to be optimized is shown in Fig.6.The antenna was fed by a 50-Ω microstrip line and printed on an FR4 substrate with a thickness of 1.6 mm,a permittivity of 4.4,and a loss tangent of 0.02.The design goal was to make sure that the isolation was more than 10 dB in the 3.5 GHz WiMAX and 5.2/5.8 GHz WLAN bands,whileS11maintained a value lower than-10 dB within working frequencies.S11is a performance indicator of the antenna.The larger the absolute value ofS11(that is,return loss),the better the impedance matching of the antenna in this frequency band,and the more the radio waves that can be transmitted.In general,ifS11＜-10 dB,the antenna can work in this frequency band.Isolation is another performance indicator of the antenna (represented byS12in dual-port antennas),referring to the degree of interference between two antennas.The greater the isolation,the less the interference between the antennas,and the better the antennas can transmit and receive radio waves.The multi-objective functions can be described as

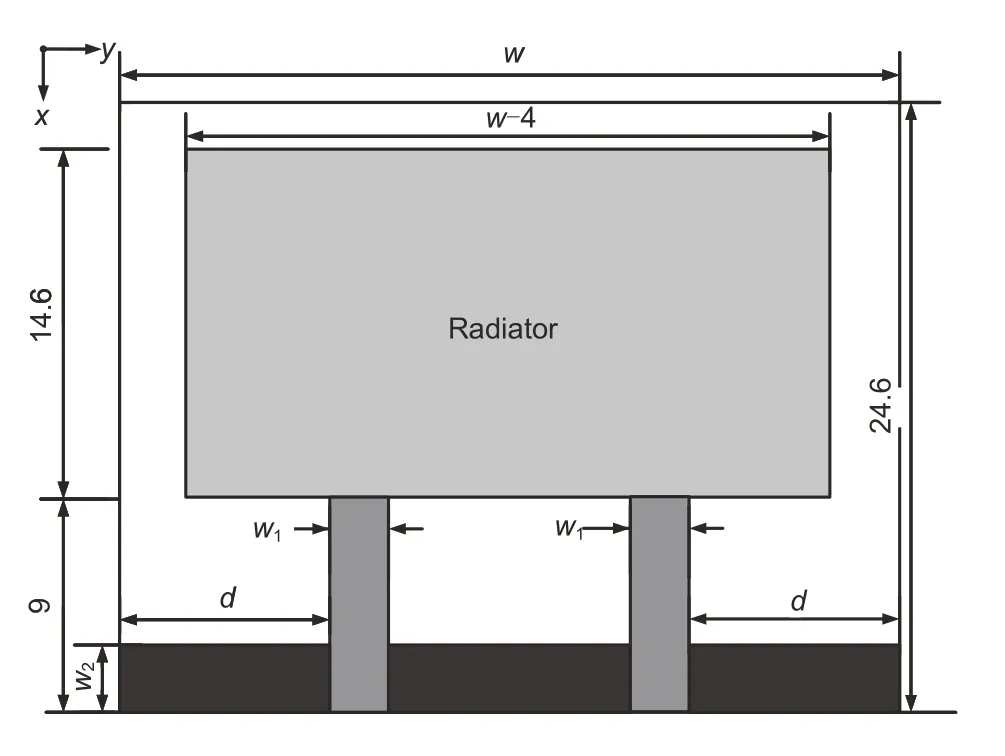
Fig.6 Initial structure of the MIMO antenna

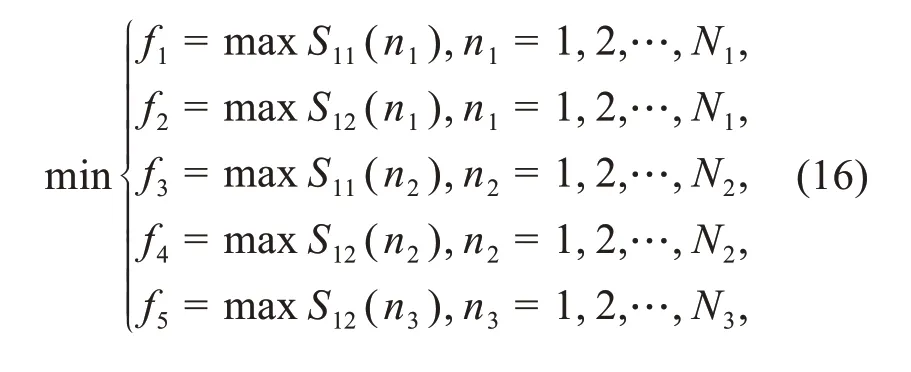
wheref1andf2are to ensure that the working frequency band around the 3.5 GHz WiMAX bands is available,whilef3andf4are for 5.2/5.8 GHz WLAN bands.The parameterf5is to ensure that the isolation is still more than 10 dB in the remaining frequency band.n1,n2,andn3are the particular sampling frequency points in the first,second,and remaining frequency bands,respectively.N1,N2,andN3represent the numbers of sampling points in the three frequency bands.

In this MIMO antenna design,the continuous variables included the width of the substratew,feederw1,and groundw2,and the distance between the feeder and substrated,where 20≤w≤30,2≤w1≤3,3≤w2≤5,and 4≤d≤6 mm.The binary parameters were related to the topology optimization of the shape of the radiator with a bilaterally symmetric structure.The left half of the radiator was dispersed into 10×10 small elements,and the size of each element was (w-4)/20×14.6/10 mm2.The overlap length of each small element was 10% of the side length to ensure the accuracy of the EM simulation.As for the parameter setting of the algorithm,the population size and iteration number were both set to 30,andΘ=0.1.The algorithm’s dimensions are composed of 100(half of the number of pixels in the radiator) binary variables and four continuous variables.Each algorithm was run independently 10 times.

Some of the MIMO antenna topologies obtained by CBMOGWO are shown in Fig.7,and their corresponding continuous design variables are shown in Table 1.Due to limited space,we present only four antenna topologies and their performance results.As seen from Fig.8,all MIMO antennas realized over 10 dB return loss and isolation levels within the preset operating frequency bands of 3.5,5.2,and 5.8 GHz.The simulation and measurement results were in good agreement with the acceptable error range.Fig.9 presents the simulated and measured radiation patterns in the three principal planes for elements 1 and 2 at 3.5,5.2,and 5.8 GHz,showing a good agreement between the simulation and measurement results.Furthermore,some complementary characteristics for the two-element patterns were observed at the same frequency,indicating the pattern diversity to combat multipath fading.Fig.10 shows the calculated envelop correlation coefficient (ECC) of the optimized MIMO antenna 2.In the whole operation band,the ECC values were better than the acceptable criterion of less than 0.3,which indicated that a desirable diversity capability was achieved by the optimized MIMO antenna.

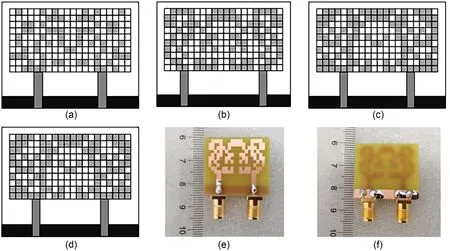
Fig.7 Part of the MIMO antenna optimized by CBMOGWO: (a) antenna 1;(b) antenna 2;(c) antenna 3;(d) antenna 4;(e)top view of the fabricated antenna 2;(f)bottom view of the fabricated antenna 2

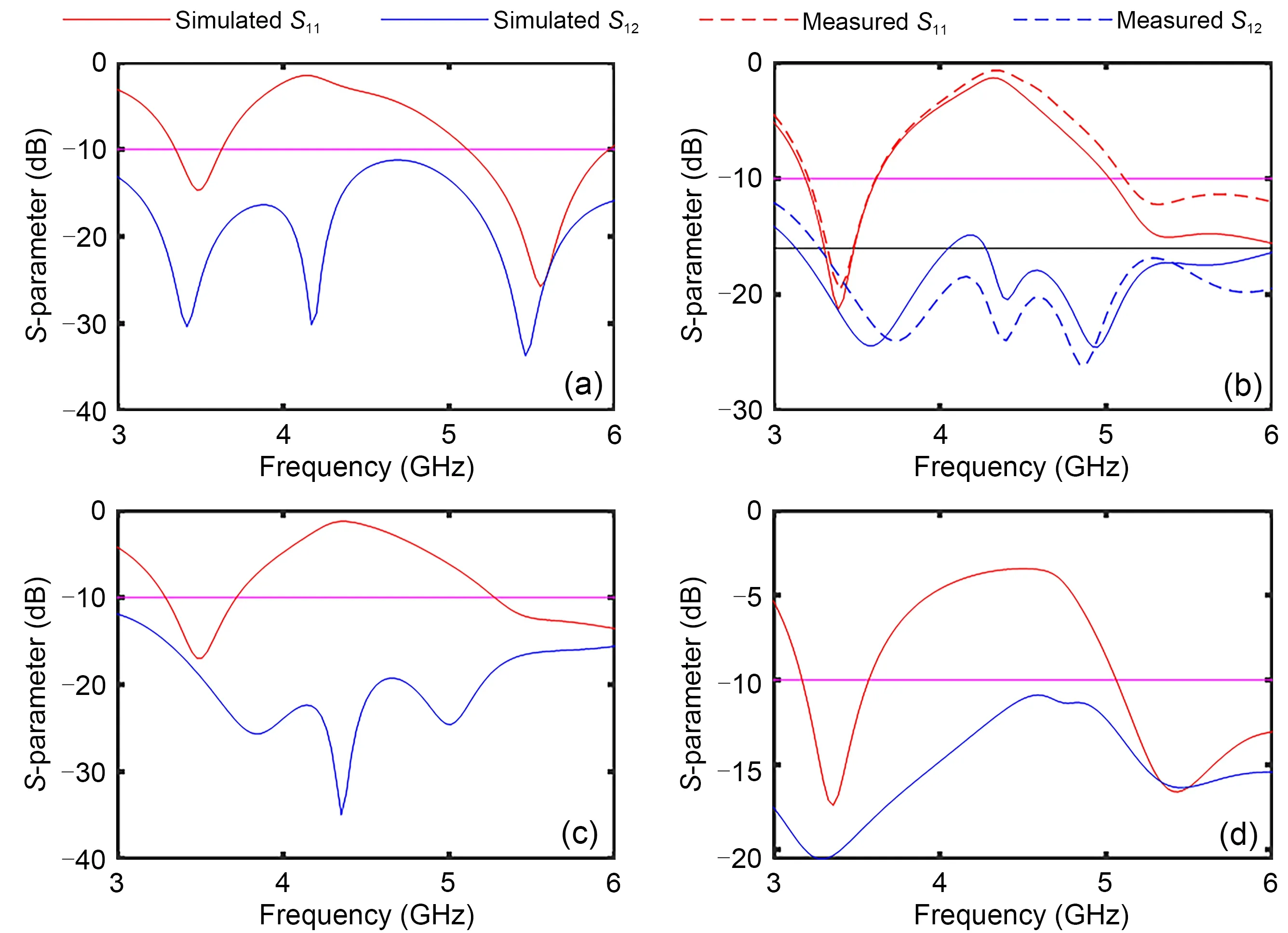
Fig.8 Simulated and measured S-parameter of the MIMO antenna(only antenna 2 is fabricated and measured):(a)antenna 1;(b)antenna 2;(c)antenna 3;(d)antenna 4.References to color refer to the online version of this figure

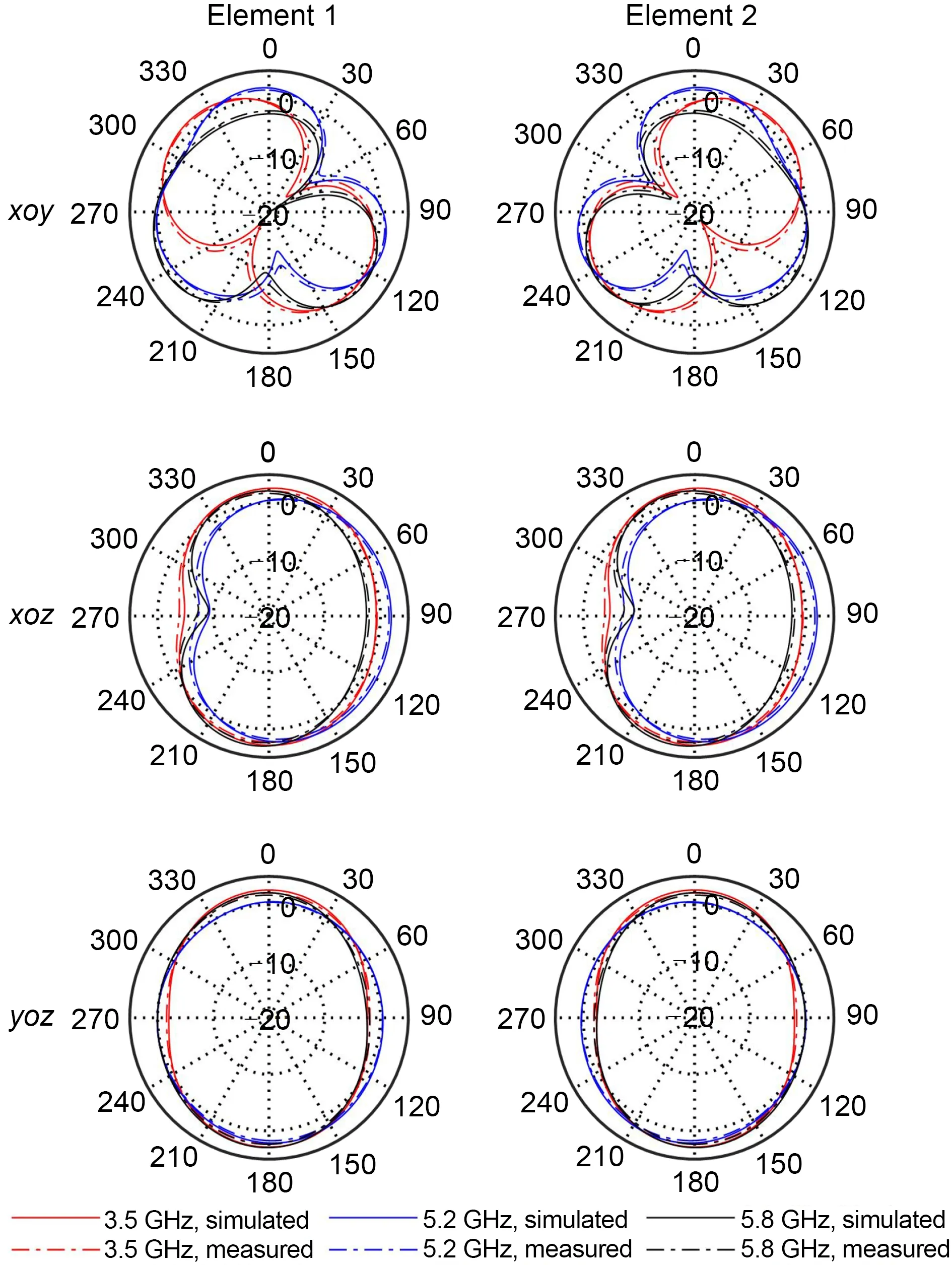
Fig.9 Radiation patterns for the obtained MIMO antenna 2 at different frequencies (elements 1 and 2 are the two element structures of the antenna).References to color refer to the online version of this figure

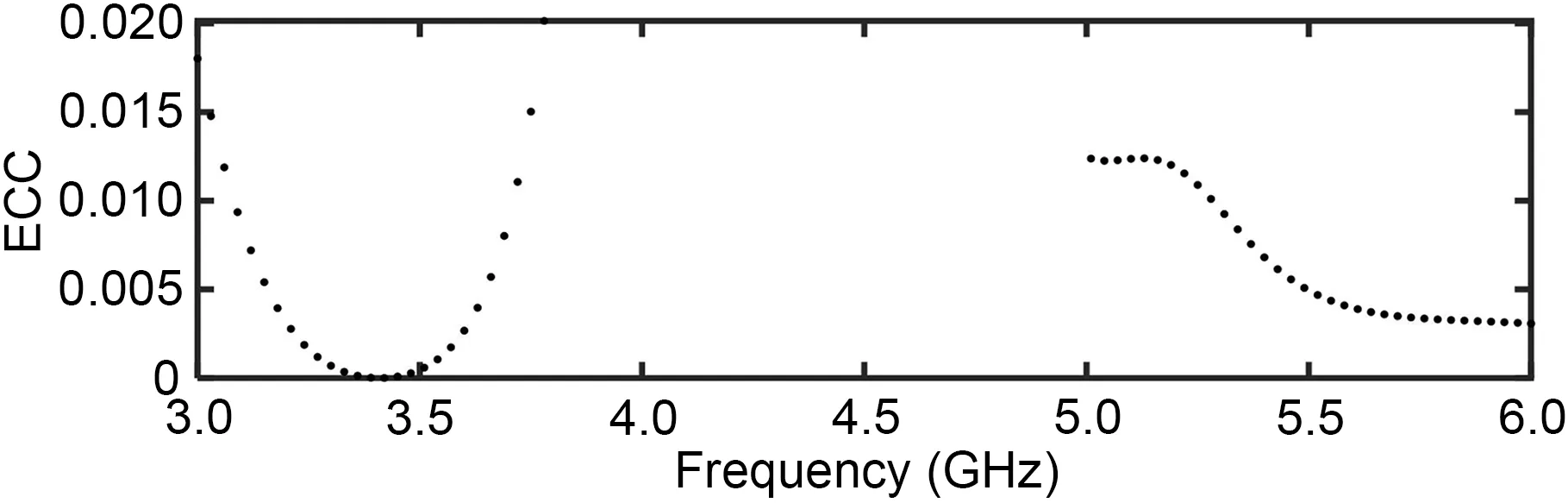
Fig.10 Calculated ECC of the optimized MIMO antenna 2

Furthermore,compared with previous MIMO antenna design results (Table 2),our designed dualband MIMO antenna had smaller size and higher isolation degree with lower design complexity.Compared with the design methods in the literature (Sharawi et al.,2012;Kumar,2016;Ding et al.,2017;Ren and Zhao,2019) that rely on antenna designers and EM software,our CBMOGWO-based design method had the lowest design complexity.In addition,compared with previous optimization methods (Table 3),our design had a higher variable dimension,more variable types,and more design objectives.Obviously,our design also had the highest complexity compared to the designs in the literature(Dong et al.,2019b;Jia and Lu,2019;Du et al.,2020).The above demonstrated that the proposed CBMOGWO is the most effective among the antenna topology designs.

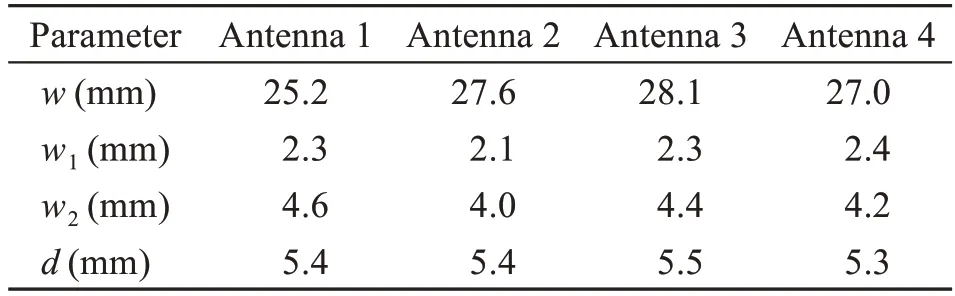
Table 1 Continuous parameters obtained in the topology optimization of the MIMO antenna

To verify the optimization capability of the proposed CBMOGWO in antenna topology optimization,we still used multi-objective metrics for evaluation.The calculation of the IGD value requires the true Pareto solution set,which is difficult to obtain for engineering optimization problems such as antenna topology optimization.Therefore,the HV value was used to evaluate the optimization ability of the three algorithms.Since the true Pareto solution set was unknown,[1,1,1,1,1] was selected as our reference point.The evolution of the average HV value of 10 times with the number of iterations is shown in Fig.11.It can be observed that the convergence curve of CBMOGWO was always higher than those of the two other algorithms.The final average HV values are shown in Table 4.The HV value of the Pareto solution set obtained by CBMOGWO was obviously larger.The above analysis demonstrates that the Pareto solution set obtained by CBMOGWO in this compact MIMO antenna topology optimization example was better compared with the original BMOGWO and traditional BMOPSO.

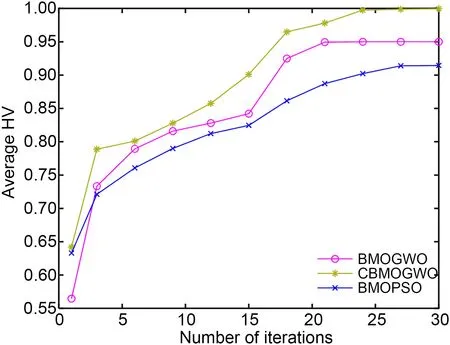
Fig.11 Evolution of the average HV value in antenna topology optimization

Next,our proposed method was compared to BMOGWO and BMOPSO in terms of CPU time.Each EM simulation took about 144 s on a 64-bit operating system with 16 GB RAM and a 3.7 GHz i5 processor.To improve the experimental efficiency,we carried out parallel calculation on the population of the algorithm in each iteration (simultaneous calculation of four populations each time was supported).In CBMOGWO,the computational cost was greatly reduced due to the reduction in the number of populations requiring location updates and the number of EM simulations.Table 4 shows that the number of EM simulations of BMOGWO and BMOPSO was 930,while that of CBMOGWO was only 570.The design time of CBMOGWO was only 59.71% of that of BMOGWO.This reduction of optimization time is significant for antenna topology optimization.

Table 2 Performance comparison between the optimized MIMO design and previous work

Table 3 Optimization comparison between the proposed CBMOGWO and previous work

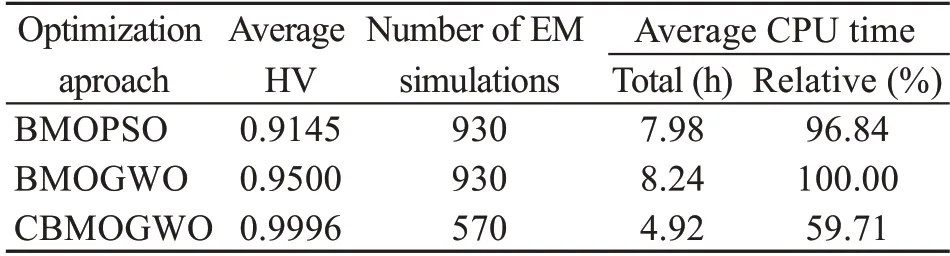
Table 4 Comparison of optimal performance and computational cost between different antenna optimizations

6 Conclusions

In this paper,an efficient and cost-effective algorithm,named CBMOGWO,is proposed for antenna topology optimization.First,the competitive mechanism is used to reduce the number of calls to EM simulation to reduce calculation costs.Then,we introduce the cosine oscillation function into the linear convergence factor of the original BMOGWO to balance exploration and exploitation.Furthermore,we verify the effectiveness of CBMOGWO on 12 standard MOTPs and four MOKPs.Finally,the high efficiency of our method in antenna topology optimization is validated with the design example of a compact dual-band MIMO antenna with high-dimensional mixed design variables and multiple objectives.CBMOGWO requires only about 60% of the time consumed by the traditional BMOGWO and BMOPSO,which shows that our method is highly adaptable even for complex design problems.It provides new ideas for fast antenna optimization design based on MOEAs with increased degree of freedom and helps explore new and unexplored antenna structures with satisfactory performance.Moreover,our proposed competition mechanism is not only applicable to BMOGWO,but can be migrated to more EAs.The proposed time-saving CBMOGWO is not limited to antenna topology optimization,but can also be applied to other computationally complex engineering problems such as filter design and microwave circuit design.In the future,we aim to explore the dimension reduction of antenna design variables to further reduce the computational cost.

Contributors

Xia YUAN designed the research.Xia YUAN and Jian DONG processed the data.Xia YUAN drafted the paper.Jian DONG helped organize the paper.Jian DONG and Meng WANG revised and finalized the paper.

Compliance with ethics guidelines

Jian DONG,Xia YUAN,and Meng WANG declare that they have no conflict of interest.

List of supplementary materials

1 Gery wolf optimizer and multi-objective grey wolf optimizer

2 Exploration and exploitation analysis

3 Procedure 1

4 Multi-objective test problems and multi-objective knapsack problems

Table S1 Bi-objective MOTPs

Table S2 Tri-objective MOTPs

Table S3 Five-objective MOTPs

Table S4 Statistical results for IGD on UF1 to UF12 on MOTPs

Fig.S1 Boxplot of the statistical results for IGD on UF1 to UF12 on MOTPs

Fig.S2 Evolution of the average IGD value on UF1 to UF12 on MOTPs

Table S5 Statistical results for HV on UF1 to UF12 on MOTPs

Fig.S3 Boxplot of the statistical results for HV on UF1 to UF12 on MOTPs

Fig.S4 Evolution of the average HV value on UF1 to UF12 on MOTPs

Table S6 Statistical results for HV on MOKPs

Fig.S5 Boxplot of the statistical results for HV on MOKPs

Fig.S6 Evolution of the average HV value on MOKPs