A power resource dispatching framework with a privacy protection function in the Power Internet of Things＊

Shuanggen LIU,Shuangzi ZHENG,Wenbo ZHANG,Runsheng FU

School of Cyberspace Security,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

†E-mail:liusgxupt@163.com;zhangwenbo@xupt.edu.cn

Abstract:Smart meters in the Power Internet of Things generate a large amount of power data.However,data privacy in the process of calculation,storage,and transmission is an urgent problem to be solved.Therefore,in this paper we propose a power resource dispatching framework (PRDF) with a privacy protection function,which uses a certificateless aggregate signcryption scheme based on cloud-fog cooperation.Using pseudonyms and aggregating users’ power data,PRDF not only protects users’privacy,but also reduces the computing cost and communication overhead under traditional cloud computing.In addition,if the control center finds that a user has submitted abnormal data,it can send a request to the user management center to track the real identity of the user.Our scheme satisfies security requirements based on the random oracle model,including confidentiality and unforgeability.Furthermore,we compare our scheme with other certificateless aggregate signcryption schemes by simulations.Simulation results show that compared with traditional methods,our method performs better in terms of the computation cost.

Key words:Power Internet of Things;Cloud-fog cooperation;Elliptic curve;Random oracle model;Certificateless aggregate signcryption

1 Introduction

Power Internet of Things (PIoT) is an industrial Internet of Things.It can connect everything with com‐puters in power systems.For example,it can connect users,power grid enterprises,and power generation enterprises with suppliers to generate shared data and to serve users,power grids,power generation suppli‐ers,governments,and society.Based on the deep per‐ception and advanced communication technology,it improves the level of precise control and intelligent dispatching of power grids.Moreover,PIoT promotes the transformation of traditional power systems to an energy Internet.The specific structure is shown in Fig.1.Power grid intelligence brings great conve‐nience to our lives.However,with the enrichment of smart grid functions and service improvements,some problems also occur.The concurrent access of a large number of terminal devices in the PIoT leads to sig‐nificant delay and low security.For example,when smart meters are used in the PIoT,the volume of electricity consumption data which is generated by many electricity meters and usually collected during the same period creates higher data storage and pro‐cessing capacity requirements.Moreover,there is a privacy protection issue when power data is transmit‐ted in smart grids(Jin,2021;Li HJ and Gao,2021).

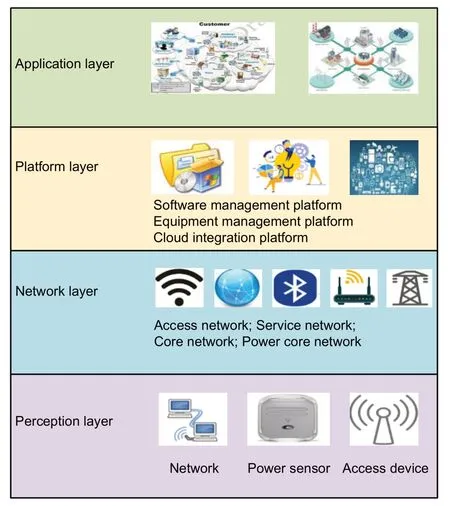
Fig.1 Structure of the PIoT

In view of the problem of data computing and storage,cloud computing can gather many comput‐ing resources on cloud platforms to form a virtual huge computing resource and data center.Users can obtain the required computing and storage resources at a relatively low cost (Cai,2021;Zhang LY,2021).However,unacceptable delay caused by long distance transmission of data makes cloud computing unsuit‐able for delay-sensitive devices.Fog computing is closer to users than traditional cloud computing.By introducing fog layers between the remote cloud lay‐ers and terminal devices,fog nodes (FNs) can use batch verification to relieve computing and storage pressure in power grids (Ma B et al.,2019;Ma JJ et al.,2021).It can also reduce the data transmission distance,data transmission delay,and the cost of data sending by terminal devices (Jia and Zhou,2018;Xu et al.,2018).

1.1 Related works

The common methods for protecting user privacy in the PIoT are anonymity,data aggregation,and adding noise.Most of existing schemes are based on homomorphic encryption (Guo et al.,2020;Shen et al.,2020;Wang XD et al.,2021;Xia et al.,2022).However,homomorphic encryption is not efficient.For resource-constrained devices,more efficient schemes should be considered.Lyu et al.(2018) and Ul Hassan et al.(2019) proposed aggregate schemes using differential privacy.Yu CM et al.(2014) pro‐posed a ring signature scheme in smart grids.Wang L(2019) proposed an aggregate signature scheme,and Wang QY et al.(2020) proposed a batch-verifiable linkable ring signature scheme.They both used digi‐tal signatures to achieve integrity and authentica‐tion.However,signatures cannot meet confidentiality requirements.User data transmitted in the PIoT should preserve confidentiality and integrity at the same time.Therefore,user data should be encrypted and transmitted in the PIoT.Sui and de Meer (2020)proposed a secure aggregate signcryption scheme based on certificates,which creates a certificate man‐agement problem.Chen (2016) proposed a scheme that combines certificateless aggregate signcryption and a masking value,which successfully solves the problem of key escrow.Xie and Li (2020) proposed a certificateless aggregate signcryption scheme with noise.On one hand,the scheme added noise to blur user data.On the other hand,low efficiency opera‐tions,such as bilinear pairing and exponential opera‐tions,were not used.Consequently,the efficiency of signature verification was improved.However,the scheme could not preserve anonymity or track the real identity of an abnormal user.

Table 1 gives an overview of existing aggrega‐tion schemes.

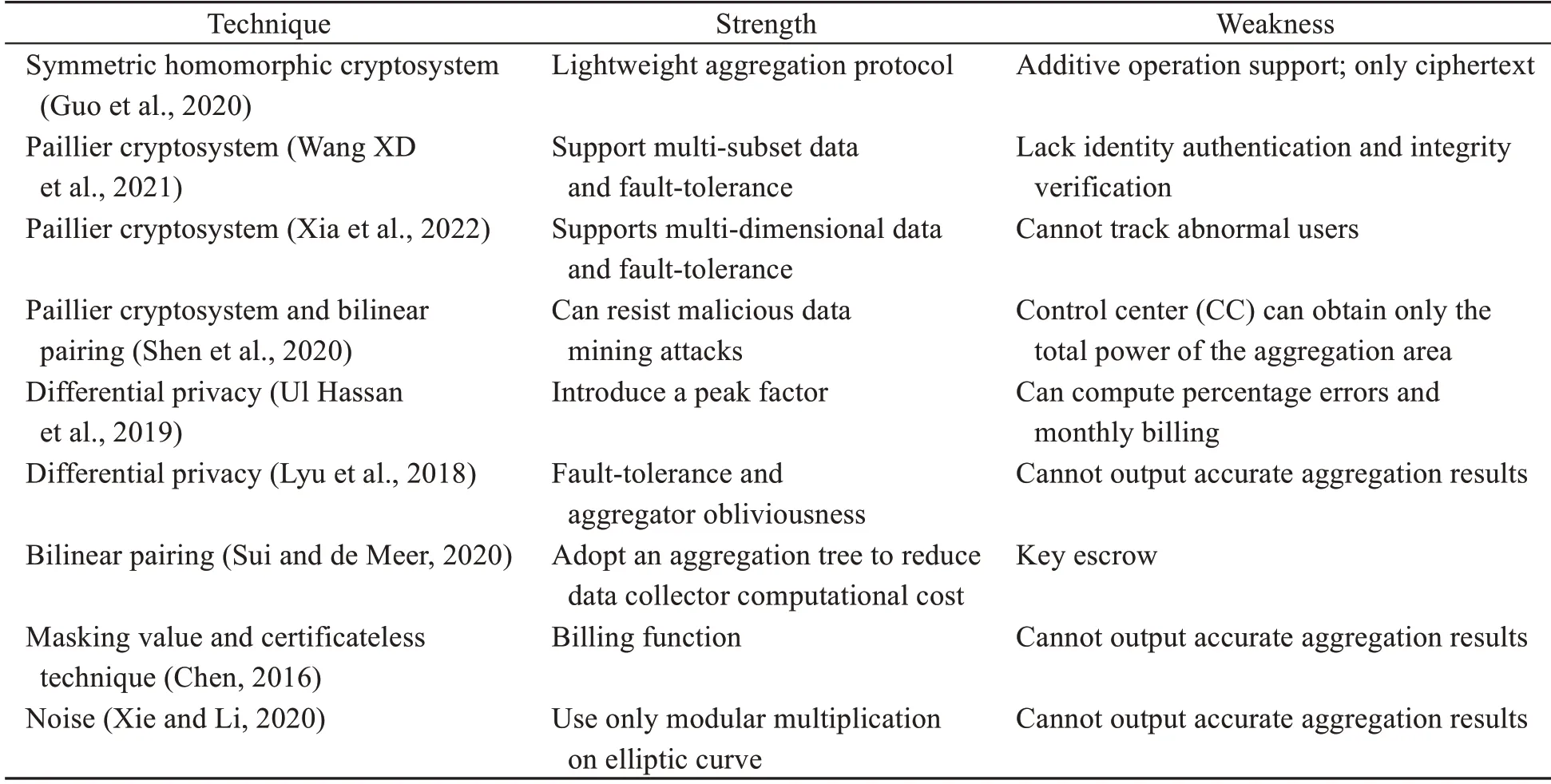
Table 1 Overview of secure aggregation schemes

1.2 Motivations

Most of existing certificateless aggregate sign‐cryption schemes are based on bilinear pairing and exponential operations.However,these two operations are much less efficient than scalar multiplication and point addition on elliptic curves.In addition,existing schemes hardly consider the anonymity of every user and the methods for tracking abnormal users.

1.3 Our contributions

To improve the efficiency and protect user privacy,in this paper we propose a power resource dis‐patching framework (PRDF).The framework uses a certificateless aggregate signcryption scheme with only scalar multiplication and point addition,by which the efficiency is improved.Moreover,users can send data anonymously,which can protect every user’s privacy.Our scheme can track the true identity of a user who submits abnormal data,which is of great significancefor managing users and protecting user privacy.The ar‐chitecture of cloud-fog cooperation in PIoT is shown in Fig.2.The main contributions of this paper are as follows:

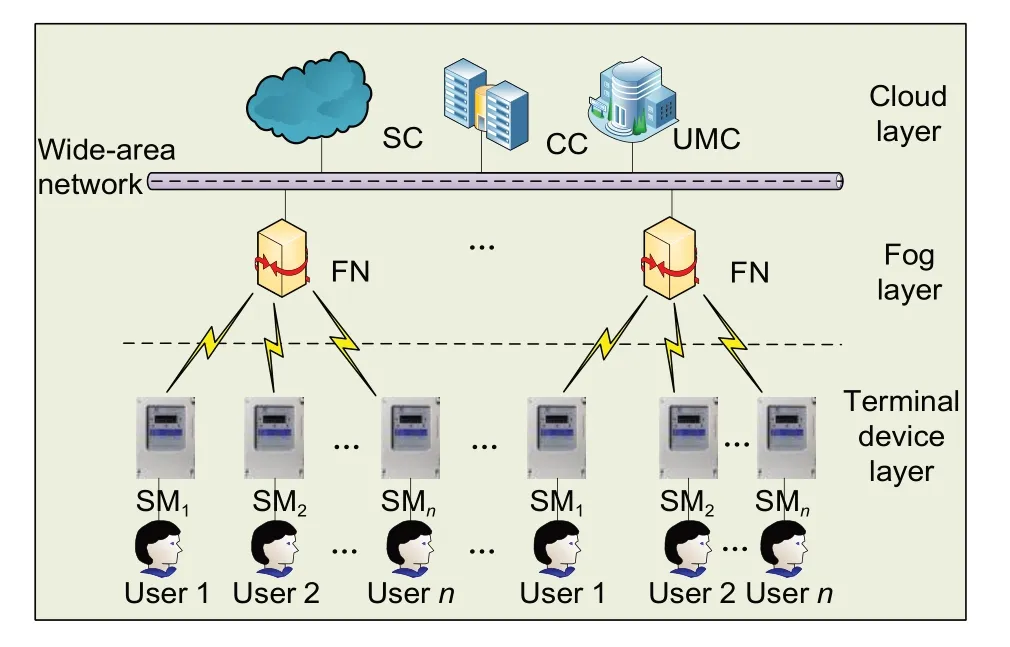
Fig.2 Architecture of cloud-fog cooperation

(1)PRDF manages power data and the real iden‐tity of users separately.In this way,it can prevent attackers from directly obtaining the corresponding relationship between the users’ identity and their data.

(2) PRDF combines the cloud-fog cooperation mode with certificateless aggregate signcryption technology using pseudonyms.Control center (CC)can analyze power consumption of the whole area and formulate the regional power dispatching strat‐egy without knowing the real identity of the users.Moreover,if a user’s data is abnormal,CC will notify the user management center (UMC) to track the abnormal user’s real identity.

2 Preparatory knowledge

2.1 Relevant difficult problems

1.Elliptic curve computational Diffie-Hellman problem(ECCDHP)

LetGbe an addition cyclic group of orderq,andpbe a generator of it.GivenaP,bP∈G,for any unknowna,b∈,calculateabP.

2.Elliptic curve discrete logarithm problem(ECDLP)

LetGbe an addition cyclic group of orderqon an elliptic curve,andpbe a generator of it.GivenP,aP∈G,for any unknowna∈,calculatea.

2.2 Formal definition

2.2.1 Frame definition

The certificateless aggregate signcryption scheme in this study consists of the following participants:storage cloud (SC),CC,key generation center(KGC),UMC,FN,and users belonging to the same aggrega‐tion area with real identity IDi(each user has a smart meter SMi).The PRDF model is shown in Fig.3.

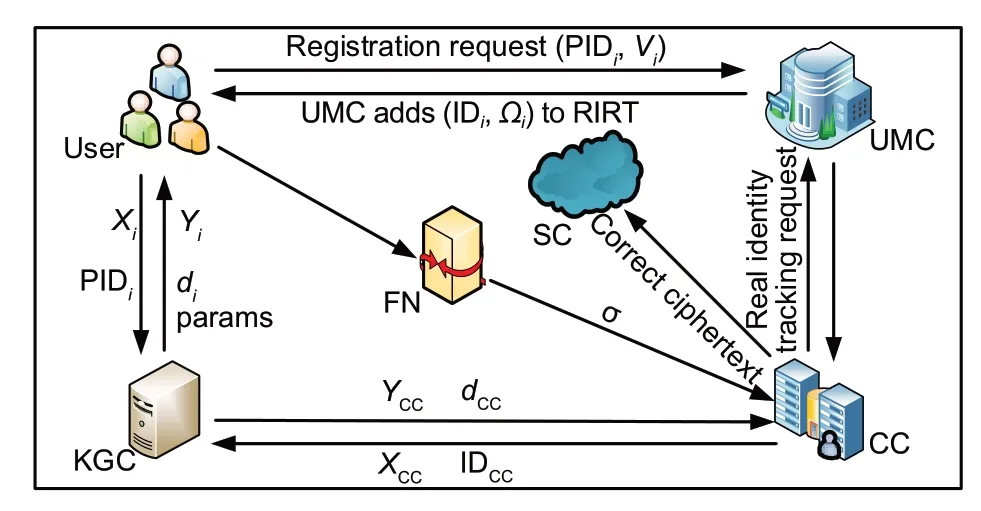
Fig.3 Model of the power resource dispatching framework(PRDF)

As shown in Fig.3,Useriexecutes the pseud‐onym generation algorithm to obtain his/her pseud‐onym PIDiand sends a registration request to UMC.Then,UMC stores (IDi,Ωi) in the real identity rela‐tionship table (RIRT) of SMi.Next,KGC and Userigenerate the full keys together.Then,Useriencrypts datami,outputs a signature,and sends the signcryp‐tion to FN.After receiving the signcryption,FN veri‐fies whether the signature is valid.After passing the verification,FN aggregates the signature and sends the aggregated result to CC,or refuses to accept it.Finally,CC decrypts the ciphertext and verifies the aggregated signature.After verifying the signature successfully,it accepts the decryption result and sends the ciphertext to SC for storage,or refuses to accept it.Moreover,if a user submits abnormal data,CC will notify UMC to track the user’s real identity.

2.2.2 Formal definition of certificateless aggregate signcryption scheme

The certificateless aggregate signcryption scheme consists of seven algorithms: system parameter gener‐ation,user’s key generation,partial key generation,signcryption,aggregation,decryption,and aggre‐gate verification.

(1) System parameter generation: Given a secu‐rity parameterk,KGC calculates a secret master keysand public parameters.

(2) User’s key generation: Userirandomly se‐lects a secret valuexito calculate public keyXi,and then sends IDiandXito KGC.

(3) Partial key generation: Entering IDiandXi,KGC generates the corresponding partial public key and partial private key,and then sends them to Useri.

(4) Signcryption: Entering the parameters,mes‐sage,IDi,private key SKi,public key PKi,and CC’s identity IDCCand public key PKCC,Usericalculates the signcryption and sends it to FN.

(5) Aggregation: Entering signcryptionsσi(i=1,2,…,n),FN aggregates signcryptionsσiintoσand sendsσto CC after the validation ofσi.

(6) Decryption: Entering parameters,ciphertextsCi,Useri’s public key PKi,IDCC,and SKCC,CC can obtain messages by decrypting ciphertexts.

(7)Aggregate verification: Entering parameters,aggregated signcryptionσ,Useri’s public key PKi,IDCC,and SKCC,CC can verify whether the aggregated signature is valid.If the verification is passed,CC accepts and sends the ciphertexts to SC;otherwise,σis discarded.

2.3 Pseudonym generation algorithm and real identity tracking algorithm

2.3.1 Pseudonym generation algorithm

When Userisends a registration request to UMC,Algorithm 1 is executed to generate a pseudonym for Useri.

2.3.2 Real identity tracking algorithm

When there are some errors in the data of Useri,CC sends a real identity tracking request to UMC.Next,UMC executes Algorithm 2 to track the real identity of the abnormal user.

2.4 Safety model

A certificateless aggregate signcryption scheme must satisfy indistinguishability under the adaptive chosen ciphertext attacks and unforgeability under the adaptive chosen message attack security in the random oracle model.Queries relevant to the sender and receiver having the same identities are not al‐lowed in the random oracle model (Yu HF and Ren,2022).In this study,all entities are semi-honest and may try to infer some useful information of users.The security model of our scheme contains two types of attackers:A1andA2.

A1can replace the user’s public key,but cannot obtain the system master private keys.It refers to ma‐licious users primarily.The proposed scheme containsA11(attacking the confidentiality of our scheme) andA12(attacking unforgeability of our scheme).

A2can obtain the system master private keys,but cannot replace the user’s public key.It refers to malicious KGC primarily.The proposed scheme con‐tainsA21(attacking the confidentiality of our scheme)andA22(attacking the unforgeability of our scheme).Definition 1(Confidentiality) Assume that adversar‐iesA1andA2cannot win Game 1 or Game 2 with a non-negligible advantage.Then the scheme is secure.Game 1(Confidentiality under adversaryA11) Sys‐tem parameter generation: Entering a security parame‐terk,challengerCexecutes the system parameter gener‐ation algorithm to generate system parameters “params”and system master keys,and sends params toA11.

Stage 1:query stage

AdversaryA11performs polynomial boundedtime queries as follows:

Public key extraction queries:A11enters the user’s identity IDifor inquiry,andCreturns the public key PKitoA11.

Private key extraction queries:A11enters the user’s identity IDifor inquiry,andCreturns the pri‐vate key SKitoA11.

Public key replacement queries:A11forges a new public key=(,)to replace the original public key PKitoA11.

Signcryption queries:A11enters messagemi,signer’s identity IDi,and receiver’s identity IDBfor inquiry,andCreturns ciphertextσitoA11.

Aggregation queries:A11enters power datami,IDi,and IDBfor inquiry.Next,Creturns aggregated signcryptionσtoA11.

Decryption queries:A11entersσand IDBfor in‐quiry.Next,Creturns power datamitoA11.

Stage 2:challenge stage

After sufficient inquiry,A11selects two plaintextsmi(i=0,1) and two user’ identities IDiand IDBwith a equal length.Cdetermines whether IDBis a chal‐lenging object.If it is not,Crejects it;otherwise,Crandomly selectsξ∈{0,1} to generate an aggregate signcryptionσtoA11.A11queries in polynomial time again adaptively.It is not allowed to execute private key extraction queries or decryption queries for IDB.

Stage 3:guess stage

A11guesses a valueξ'.Ifξ'=ξ,A11wins the game.

Game 2(Confidentiality under enemyA12) The query phase is similar to that in Game 1,except that public key replacement query and private key extraction query for IDBcannot be performed.

The challenge phase and guess phase are the same in Game 1.Finally,A12wins the game.

Definition 2(Unforgeability) Assume that polyno‐mial time adversariesA1andA2cannot win Game 3 or Game 4 with a non-negligible advantage.Then the scheme is secure.

Game 3(Unforgeability under enemyA21) The sys‐tem parameter generation stage and inquiry stage are the same as those in Game 1.

Forgery stage:After the previous two stages,A21outputs a forgery signatureσ*.At least one userdoes not execute private key extraction queries and IDBdoes not execute signcryption queries.Then,A21wins the game.

Game 4(Unforgeability under enemyA22) The sys‐tem parameter generation and query phases are the same as those in Game 2.The forgery phase is the same as that in Game 3.Finally,A22wins the game.

3 Concrete scheme

3.1 Description of symbols

Symbols used in this paper are described in Table 2.

Table 2 Description of symbols

3.2 Scheme description

(1)System parameter generation

KGC executes Algorithm 3.KGC selects an el‐liptic curveE:y2=x3+ax+b.Entering a securityparameterk,KGC generates two large prime numberspandq.qis the order of the cyclic groupGonEandpis a generator ofG.KGC selects a random numbersas the system master key and generates the system parameters params=(G,p,q,P,Ppub,H1,H2,H3),as shown in Algorithm 3.

(2)User’s key generation

Useriexecutes Algorithm 4.

(3)Partial key generation

KGC executes Algorithm 5.KGC selects a ran‐dom numberand generates partial public keyYifor Useri.In addition,KGC takesYias a parameter to generate partial private keydiof Useri.Finally,KGC sends (Yi,di) to Useri.Useri’s public key is PKi=(Xi,Yi) and his/her private key is SKi=(xi,di).In this scheme,CC obtains its key in the same way as Useri.Its public key is PKCC=(XCC,YCC)and its private key is SKCC=(xCC,dCC).

(4)Signcryption

Useriexecutes Algorithm 6.Useriselects a ran‐dom numberri∈and calculatesRi,Ui,Ci,andsi.Finally,Userisendsσi=(Ri,si,Ci,t)to FN.

(5)Aggregation

After receiving signcryptionsσi(i=1,2,…,n),FN verifies the time stamp of eachσi.If the time stamp is invalid,the ciphertext is discarded;other‐wise,FN executes Algorithm 7.

(6)Decryption

CC takes the pseudonym,public key,and ci‐phertext as parameters,and then executes Algo‐rithm 8 to obtain PIDi||mi||t.

(7)Aggregation verification

CC verifies the signature by executing Algo‐rithm 9.If the result is true,the message PIDi||mi||tis valid;otherwise,the message is rejected.

4 Proof of correctness,availability,and security

4.1 Proof of correctness and availability

(1)Correctness

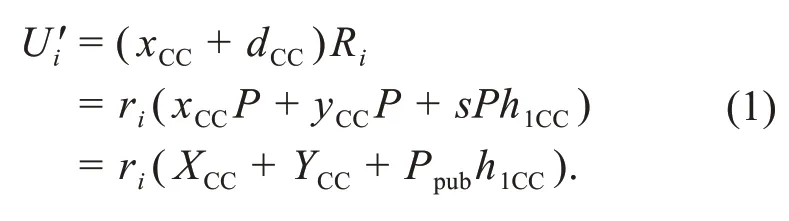
(2)Availability

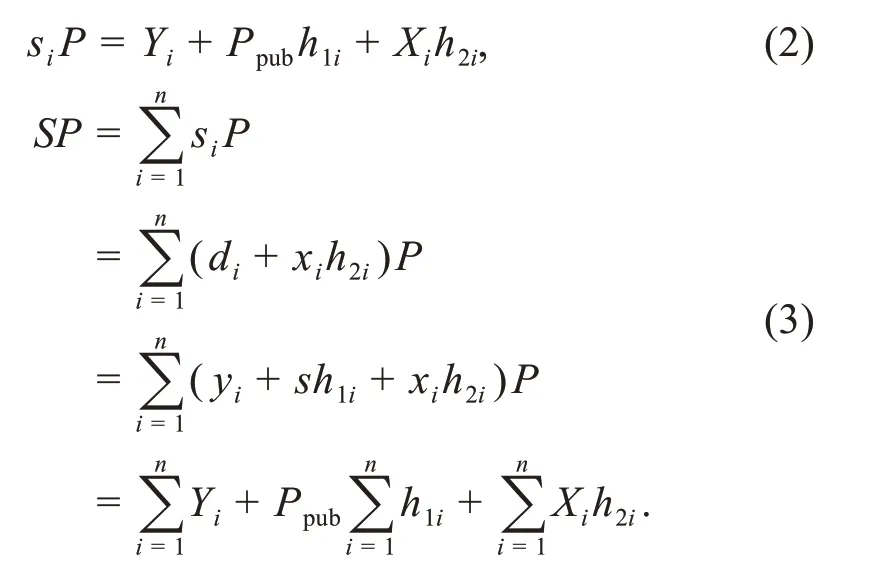
4.2 Proof of security

In this study,we will prove the confidentiality of the proposed scheme based on ECCDHP and ECDLP under the random oracle model.

Theorem 1(Confidentiality under adversaryA11)In a random oracle model,the unforgeability of the proposed scheme can be broken if adversaryA11can win Game 1 in polynomial time with a non-negligible probabilityε11(in the game,A11can doqssigncryption queries andqskprivate key extraction queries at most).Then algorithmQcan solve ECCDHP in polynomial time with at least a non-negligible probabilitywhere e is the base of the natural logarithm andkis a security parameter.

ProofQis a solver of the ECCDHP.Given the input (P,aP,bP),its goal is to obtainabPwhena,b∈and are unknown.Quses adversaryA11as a challenger for Game 1.After announcing the start of the game,Qexecutes the system parameter generation algorithm and sends the public parameters params toA11.LetPpub=aP,and letaact as the system master key.In addition,Qmaintains listsL1,L2,L3,LSK,andLPK,which are used to track the inquiries ofA11aboutH1queries,H2queries,H3queries,private key extraction queries,and public key extraction queries,respectively,for the oracle model.Initially,each list is empty.

Stage 1:query stage

AdversaryA11performs polynomial boundedtime queries as follows:

Probabilistic analysis:Qsolves ECCDHP suc‐cessfully,which means that it does not stop the simu‐lation all the time and adversaryA11breaks through the confidentiality of the proposed scheme with a non-negligible probabilityε11.Qwill succeed only if the following events do not occur:

ProofQis a solver of ECCDHP.Given the input(P,aP,bP),its goal is to obtainabPwhena,b∈and are unknown.Quses adversaryA12as a challenger to the game.After announcing the start of the game,Qexecutes the system parameter generation algorithm.Next,Qsends the public parameters params and the master keystoA12.In addition,QmaintainsL1,L2,L3,LSK,andLPK,which are used to track the inquiries ofA12aboutH1queries,H2queries,H3queries,private key extraction queries,and public key extraction queries for the oracle model,respectively.Initially,each list is empty.

Stage 1:query stage

We present the proof of the unforgeability of our certificateless aggregate signcryption scheme based on ECDLP under the random oracle model.

ProofQis a solver of ECDLP.Given the input(P,aP),its goal is to obtainawhena∈and is unknown.Quses adversaryA21as a challenger to Game 3.After announcing the start of the game,Qexecutes the system parameter generation algorithm and sends the public parameters params toA21.LetPpub=aP,and letaact as the system master key.In addition,Qmaintains listsL1,L2,LSK,andLPK,which are used to track the inquiries ofA21aboutH1queries,H2queries,private key extraction queries,and public key extraction queries for the oracle model,respectively.Initially,each list is empty.

Stage 1:query stage

AdversaryA21performs polynomial boundedtime queries as follows:

AdversaryA21performsH1queries,H2queries,public key extraction queries,private key extraction,and public key replacement queries.

Signature queries: WhenQreceives a signature query fromA21,it looks for(PIDi,Xi,Yi,ci)inLPK.

Ifci=1,the query ends and the simulation terminates.

Otherwise,Qlooks for the private key SKi=(xi,di) of PIDiinLSKand executes the signcryption algorithm to generateσi=(Ri,si,Ci,t)forA21.

Stage 2:challenge stage

QinquiriesLPKfor (PIDi,Xi,Yi,ci).Ifci=0,the query ends and the simulation terminates.

Probabilistic analysis:Qsolves ECDLP success‐fully,which means that it does not stop the simula‐tion and adversaryA21breaks through the unforge‐ability of this scheme with a non-negligible probabilityε21.Qchallenges successfully only with the follow‐ing events:

ProofQis a solver of ECDLP.Given the input(P,aP),its goal is to obtainawhena∈and is unknown.Quses adversaryA22as a challenger of the game.After announcing the start of the game,Qexecutes the system parameter generation algo‐rithm and sends the public parameters params andstoA22.In addition,Qmaintains listsL1,L2,LSK,andLPKto track the inquiries ofA22,includingH1que‐ries,H2queries,private key extraction queries,and public key extraction queries,respectively.Initially,each list is empty.

Stage 1:query stage

AdversaryA22performs polynomial boundedtime queries as follows:

AdversaryA22performsH1queries,H2queries,public key extraction queries,private key extraction queries in Theorem 2,and public key replacement queries in Theorem 3.

Signature verification inquiry:Qlooks for(PIDi,Xi,Yi,ci)and(PIDB,XB,YB,cB)inLPK.

5 Scheme analysis

5.1 Safety characteristic analysis

1.Eliminating key hosting

This scheme adopts the certificateless technology.When a user provides his/her identity information,KGC takes the master keysand the user’s identity information as parameters to generate a partial pri‐vate key for the user.The secret value selected by the user and the partial key from KGC form the whole key for the user.Consequently,the problem of key hosting is solved.

2.Resistance to replay attack

When a third party intercepts a request packet of the encryption processing sent by the client to the server,it cannot decrypt the data acquired,but can re‐peatedly send the package to the server for repetitive request operations (Ramanan et al.,2021).A server without a replay attack prevention function may in‐crease pressure and lead to data disorder.Therefore,our scheme adds a time stamp in the signcryption to effectively prevent replay attacks.

3.Relief distributed denial-of-service (DDoS)attacks

The structure of PRDF is based on cloud-fog cooperation mode.By introducing fog layer devices between cloud and the terminal devices,the distributed computing and storage of fog computing can allevi‐ate problems like the large transmission distance of traditional cloud computing and vulnerability to DDoS attacks.

Table 3 shows a comparison of safety character‐istics of different schemes for the PIoT.

5.2 Performance analysis

When comparing the computational efficiency of signcryption schemes,assuming thatnusers par‐ticipate in the signcryption and that the computational overhead depends mainly on the following opera‐tions:Ee(exponent arithmetic),Ep(bilinear pairing operation),Em(multiplication of points defined on el‐liptic curves on groupG),andEa(addition of points defined on elliptic curves).The computational overhead ofEpis more than 10 times that ofEm.A huge number of PIoT users lead to a large amount of elec‐tricity data to aggregate.Therefore,our work does not useEeorEp.The computational overhead de‐pends mainly onEmandEa.

To compare the performance of different schemes quantitatively,the execution time ofEp,Em,andEais obtained through experiments.The execution time of each operation is shown in Table 4.These operations are executed in a laptop with the In‐tel®CoreTMi7-6700HQ 2.59 GHz processor,8 GB RAM,and Windows 10 operating system.The elliptic curve isy2=x3+ax+bmodp,wherepis 160 bits.

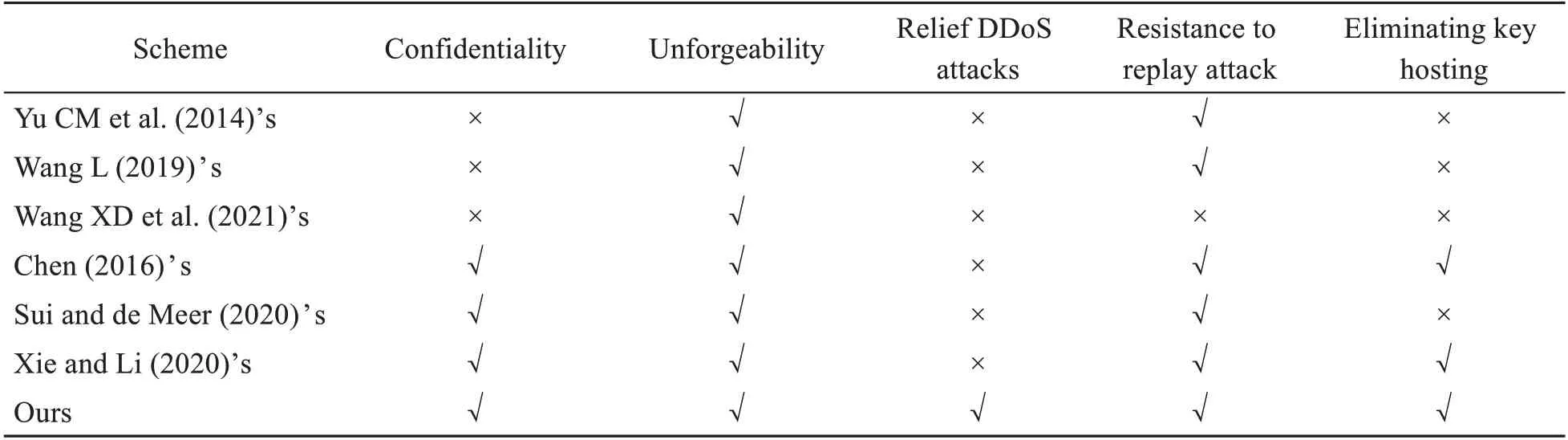
Table 3 Comparison of safety characteristics

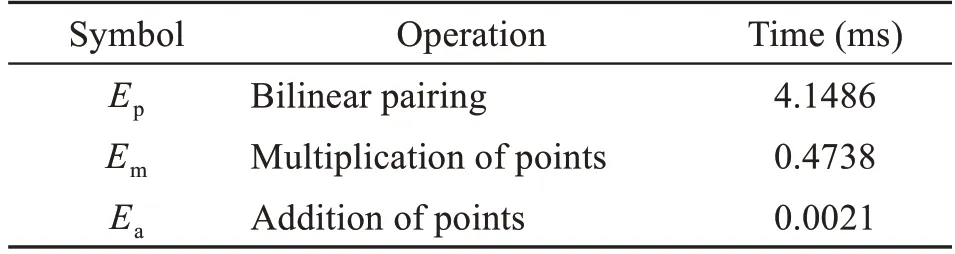
Table 4 Execution time

The performance of existing methods and the length of ciphertexts are shown in Table 5.The length of ciphertexts represents the communication overhead of each scheme.To analyze the perfor‐mance of every scheme under the same condition,we assume that the length of plaintexts is the same aslm.The communication overhead in the literature(Zhang SM et al.,2018;Cui et al.,2019;Nkenyereye et al.,2019;Yu HF and Ren,2022)is the same in this study;it is=640 bits.The ciphertext of Li C and Qi (2020) contained aggregated broad‐cast values and Kim et al.(2020) used the generating elements of two groups to calculate the signcryption of Useri.Therefore,their communication cost is the highest,=960 bits.

The signature and aggregation cost of our work is lower than that of Cui et al.(2019)’s scheme,but the decryption and verification efficienies are higher.The decryption and verification cost is lower than that in Li C and Qi (2020),but the signcryption and aggregation efficiencies are higher.Moreover,the length of ciphertext in our work is shorter than that in Li C and Qi (2020).The efficiency comparison is shown in Table 5 (the ciphertext length in each scheme includes the plaintext lengthlm,so we give only the parts other thanlm).

Table 5 Efficiency comparison among certificateless aggregate signcryption schemes

In the simulations,n(the number of users be‐longing to the same FN) is set to 1000 in Fig.4.Fig.5 shows the comparison of the calculation cost of each scheme whennis different.As can be seen from Figs.4 and 5,our scheme has more advantages compared with the other schemes.

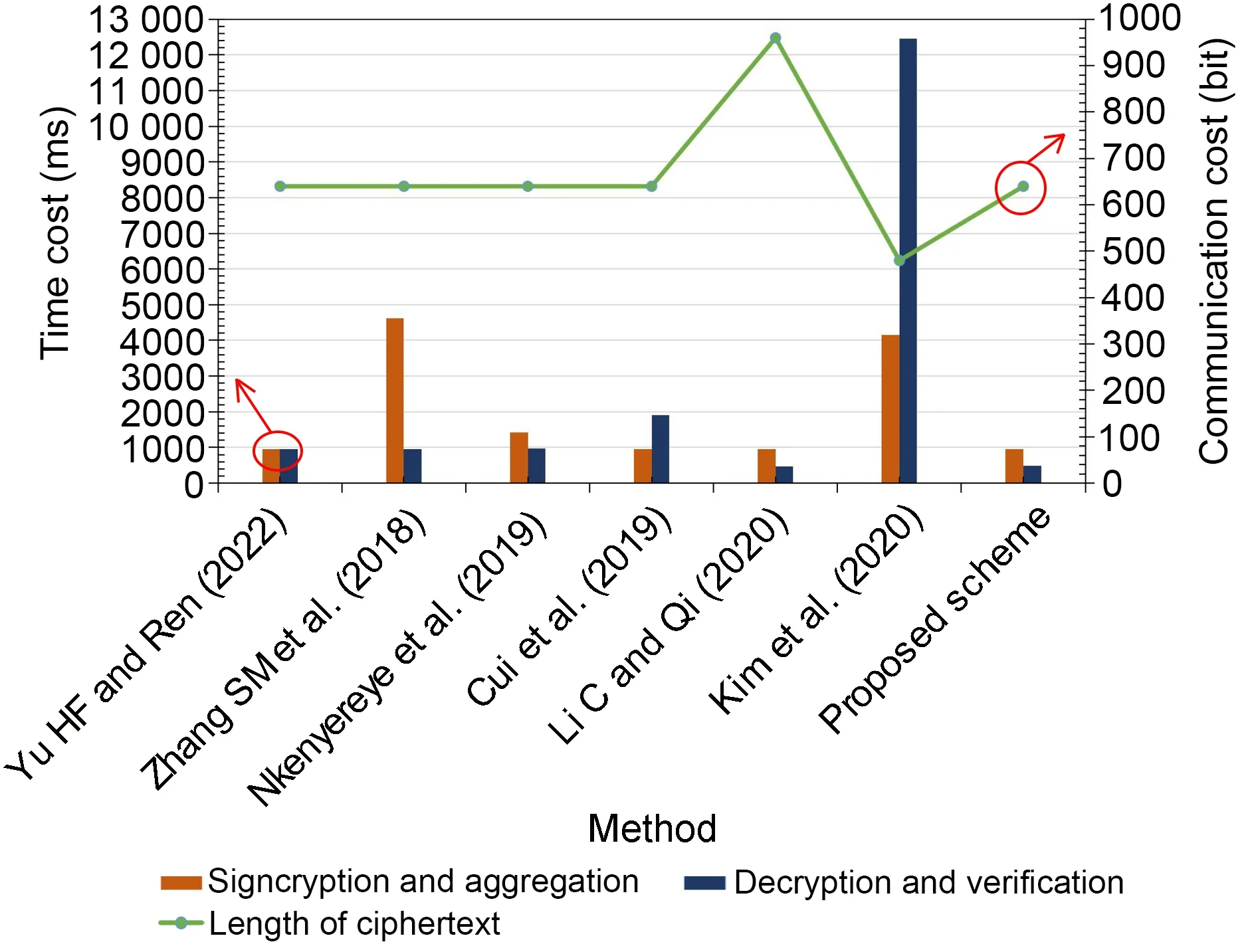
Fig.4 Comparison of calculation and communication costs of each scheme

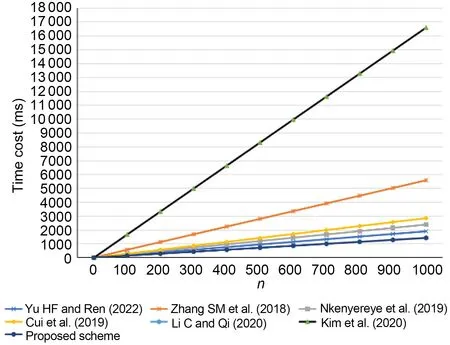
Fig.5 Comparison of calculation time cost of each scheme(0≤n≤1000)

6 Conclusions

To solve the privacy protection problem of users’power data in the PIoT and provide users with exclu‐sive power services,in this paper we proposed PRDF with a privacy protection function.PRDF is effec‐tive for facilities in the PIoT.Theoretical analysisand simulation results showed that our scheme is more efficient and has more security characteristics.

Contributors

Shuanggen LIU designed the research.Shuangzi ZHENG and Wenbo ZHANG processed the data.Shuangzi ZHENG drafted and organized the paper.Shuangzi ZHENG and Runsheng FU revised and finalized the paper.

Compliance with ethics guidelines

Shuanggen LIU,Shuangzi ZHENG,Wenbo ZHANG,and Runsheng FU declare that they have no conflict of interest.