影像测量中大视场相机畸变精确校正研究

曾志强，冯鹏鹏，李忠华

(中北大学机械工程学院，山西太原 030051)

0 前言

影像测量是基于机器视觉技术从图像中获取有用信息，从而实现测量、检测等目的。随着智能化机械发展[1]，检测和测量大尺寸零件是影像测量技术面临的又一挑战。大视场相机由于其视场较大，必然导致视场边缘处存在较大畸变。标定是保证影像测量精度的关键，而用于标定大视场相机的大规格标定板生产制造困难、标定精度较低，小规格标定板则存在标定不完全等现象，导致影像测量中大视场相机对大尺寸零件的局部精密区域(0～20 μm)测量数据不准确[2]。例如，对于大尺寸电路板上的排线检测，如果检测精度不够，容易造成误检、漏检等严重后果。另外，将相机光轴垂直下方像素当量值作为整个相机视场像素当量值，忽略像素当量值变化，也会严重影响测量结果的准确性。

针对影像测量中大视场相机的校正问题，学者进行了多方面研究。ZHANG等[3]研究了不同规格标定板对大视场相机标定结果的影响。张敏等人[4]在Hough空间中提出熵函数测量未失真曲线的直线度，计算出失真参数和畸变中心并完成对图像的校正。LI等[5]利用基于BP神经网络的近似连续函数算法得到理想图像和畸变图像之间的坐标变换函数，实现了光学畸变校正。LIAO[6]通过最小二乘算法对大视场环形透镜形成的切向图像畸变进行了校正。SAHIN和TANGUAY[7]使用空间频率等相关系数，在图像畸变校正后选择误差较大的失真测量值作为约束条件提高图像质量。KAYNIG等[8]提出一种脊线回归的校准方法，以补偿大型CCD摄像机的非线性透镜畸变。柯丰恺等[9]采用优化凸松弛多项式对相机进行了标定。祝汉锋[10]根据共线方程推导出宽视场相机的几何校正数学模型，并对相机和图像进行几何校正。以上大多数研究都是通过改进相关算法提高大视场相机标定精度，在实际工程应用中较难理解，标定过程繁琐。

本文作者针对影像测量中大视场相机畸变校正进行研究。利用棋盘格标定板和图像中心像素当量值建立转化坐标系和映射关系矩阵；然后，对标定物相邻各圆心距离进行测量；分析测量误差，建立误差补偿模型。研究结果对大视场相机测量精度提升以及畸变校正研究具有一定意义。

1 方法理论

在此研究中，主要涉及到相机标定、图像畸变以及映射矩阵建立3个研究理论。

1.1 相机标定

目前多数相机成像模型都是基于小孔成像原理建立的，物体通过一定比例投影在图像面，如图1所示。理想状况下，位于相机光轴处的投影过程为直线投影过程。相机成像过程涉及4个坐标系，标定就是4个坐标系之间的转换以及求解过程，坐标系之间的关系如图2所示。

图1 成像模型

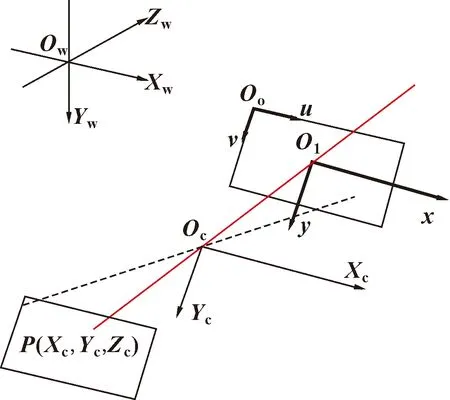
图2 坐标系示意

其中，f为相机焦距;z为物体到相机的物距。

其中：OwXwYwZw为世界坐标系;OcXcYcZc为摄像机坐标系;O1xy为图像物理坐标系，Oouv为图像像素坐标系。

1.2 图像畸变

在采集图像过程中，由于相机自身透镜非理想特征以及成像仪与透镜的非平行关系，会形成径向畸变和切向畸变，导致图像不能反映真实状态[11]。而增大相机视场会加大边缘处图像的拉伸或内缩，使用标定过程所得的相机内外参数，很难实现对图像的完全校正。在实际工程应用中，通常忽略像素当量值随相机视场发生的变化，将相机光轴垂直下方处像素当量值作为整个图像的像素当量值，也会导致图像处理结果失真[12]。

为提高处理精度，需对图像进行高精度校正。相比较而言，径向畸变对图像影响较大。径向畸变分为枕形畸变和桶形畸变，如图3所示。

图3 正常图像与畸变图像对比示意

径向畸变数学模型为

Xu=Xd+Xd(k1r2+k2r4+k3r6+…)

(1)

Yu=Yd+Yd(k1r2+k2r4+k3r6+…)

(2)

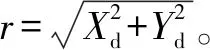
通过分析知沿图像边缘对角线处畸变最大，校正难度也最大。因此，本文作者主要分析影像测量中大视场相机视场对角线边缘处校正不完全对测量的影响，并提出误差补偿模型，以提高测量精度。

1.3 映射关系建立

1.3.1 求取特征点坐标

经分析，相机畸变若完全校正，则理想图像中任何位置的像素当量与畸变最小处的相机光轴正下方即图像中心像素当量相等或近似。基于此，在相同采集条件下，采集外形尺寸与相机视场大小接近的棋盘格标定板图像(见图4)。经校正后，求得棋盘格标定板中各交点在校正不完全图像中的坐标，并根据公式(3)将它转化到XOY坐标系中，得到(Px,Py)。图像坐标系RO1C以图像左上角为坐标原点建立。为方便建立坐标映射关系，以棋盘格图像中心为坐标原点建立转化坐标系XOY(见图5)。

图4 棋盘格标定板 图5 坐标系示意

将校正不完全图像中的坐标转化到XOY坐标系中的公式为

(3)

其中：(Px,Py)为交点在转化坐标系XOY中的坐标；(Row,Col)为交点在图像坐标系RO1C中的坐标;(Rc,Cc)为棋盘格标定板图像中心在RO1C坐标系中的坐标。

棋盘格标定板中各交点在转化坐标系XOY中的坐标求取公式为

L=N×a

(4)

其中：L为实际物理距离；N为图像中像素个数；a为像素当量值。

棋盘格标定板中正方形实际边长为30 mm，将标定所得相机光轴正下方像素当量0.114 1 mm作为大视场相机完全校正的图像全局像素当量。然后，通过公式(4)求出各交点在转化坐标系XOY中的坐标(Qx,Qy)。

1.3.2 建立映射矩阵

棋盘格标定板交点坐标转化到XOY坐标系后，(Px,Py)为校正不完全图像中的交点坐标，(Qx,Qy)为理想校正完全图像中的交点坐标，且两图像中每个交点坐标一一对应。根据其对应关系,建立映射矩阵：

(5)

其中：i为棋盘格标定板中第i个交点；M为映射矩阵。由于坐标提取存在一定误差或其他未知因素，为保证映射矩阵M的准确性，文中求取各交点对应坐标(Pxi,Pyi)与(Qxi,Qyi)在距离最小情况下的映射关系。

2 实验平台和数据分析

文中实验平台为本文作者所在课题组自行搭建的全自动影像测量仪，所有实验数据都从该实验平台上获取。

2.1 实验平台

为解决当前影像测量仪相机视场小、不能满足较大零件尺寸测量的问题，该课题组开发了全自动影像测量仪[13]，如图6所示。其基本特征是在现有影像测量仪基础上搭载一个视场较大的视觉系统(由日本Computer型号为M0814-MP的百万像素定焦镜头和型号为MV-EM510M的工业相机组成)，使测量仪能够识别较大尺寸零件类型以及确定其摆放位置的角度和坐标。通过摇杆控制，置物平台能够实现水平面上X、Y方向的移动。

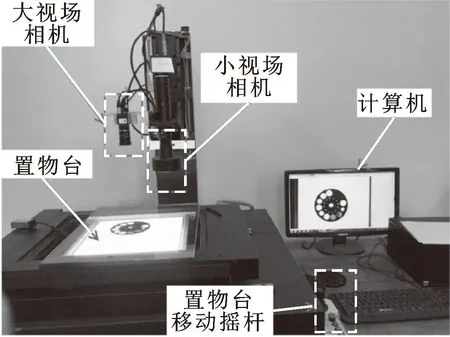
图6 全自动影像测量仪

2.2 大视场相机畸变校正不完全分析

基于该课题组自行开发的全自动影像测量仪，对影像测量中的大视场相机(视场范围为300 mm×280 mm)进行标定，并分析相机视场中心以及边缘处像素当量值。

相机标定方法有张正友标定法、Tsai两步标定法等[14]，本文作者采用如图7(a)所示的9×9圆点阵列标定板对大视场相机进行标定。

通过多次标定，得出相机光轴正下方像素当量均值为0.114 1 mm。保持相机位姿不变，采集共15个圆且相邻圆心距离为6 mm的标定物(见图7(b))在相机视场中心以及两条对角线上靠近图像边缘处的图像，如图8所示。

图7 9×9圆点阵列标定板和标定物

使用标定所得的相机内参对标定物图像进行校正，忽略图像中像素当量值变化。使用图像中心像素当量值对标定物中各相邻圆心距离进行计算，比较其相邻圆心的测量结果，如图9所示。

从图9可知：在相机视场中心a处各相邻圆心距离测量结果发生突变较小即图像校正情况良好，最大测量误差为29.3 μm，；位于相机光轴垂直处的第6、7圆心间隔的测量值最接近实际物理距离6 mm，此处图像畸变最小；而在其他相机视场边缘处所测得的相邻圆心数据均发生较大突变，且极差均约为70 μm。由以上分析可得，大视场相机存在畸变矫正不完全现象。

图9 不同位置标定物相邻圆心距离(映射前)

2.3 映射数据以及误差补偿

根据公式(5)，利用棋盘格在校正完全以及不完全情况下的各交点坐标所求出的映射矩阵为

M=

将校正不完全标定物图像中各圆心坐标通过公式(3)转化到XOY坐标系。利用映射矩阵M得到在相机校正完全图像中各圆心坐标，再次对相邻圆心距离进行测量，结果如图10所示。

图10 不同位置标定物相邻圆心距离(映射后)

从图10可知:标定物位于相机视场a处时各相邻圆心距离测量值均接近6 mm，其中最大测量误差为17.7 μm，较未校正完全图像误差减少39.6%；其他位置各相邻圆心距离数据均未发生较大突变，测量极差均约为30 μm，图像边缘处校正数据鲁棒性提高。

通过分析边缘处标定物相邻各圆心在XOY坐标系的距离，结合公式(1)(2)，利用MATLAB软件，提出一种误差补偿模型。

假设相邻圆心实际距离为y，补偿值为Δy、补偿后的相邻圆心实际距离为yt，则补偿公式为

yt=y+Δy

(6)

Δy=ax2+bx+c

(7)

其中：x为标定物相邻圆心在图像坐标系XOY的距离。通过求取x，利用最小二乘法对公式(7)进行拟合，得到方程:

Δy=0.161 6x2-16.957 4x+444.893 8

(8)

使用该补偿公式对图像边缘处相邻圆心实际距离进行补偿，结果如图11所示。

图11 映射及补偿后的相邻圆心距离

从图11可看出：补偿后的标定物在图像边缘处相邻圆心距离测量值均无较大突变且接近真实值6 mm，测量值误差均在20 μm以内且在17 μm以内的数据为91.43%。

3 补偿实验证明

为进一步证明文中影像测量中大视场相机校正方法的正确性以及误差补偿的有效性，将标定物水平放置在相机视场边缘位置进行相邻圆心距离测量，如图12所示。

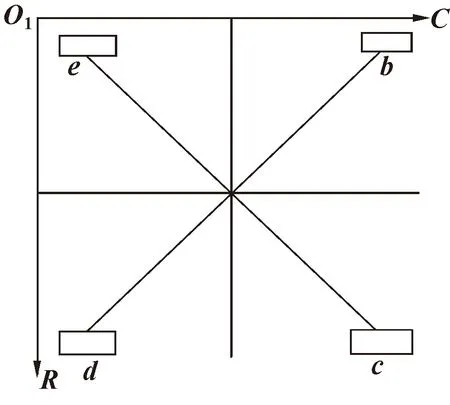
图12 补偿实验位置示意

由图13可以看出：经过坐标映射以及误差补偿后，标定物相邻圆心距离测量值均接近真实值6 mm，测量误差在17 μm以内的数据为94.64%，较好地证明了本文作者所提的大视场相机校正方法以及误差补偿公式的重复精度和可靠性。

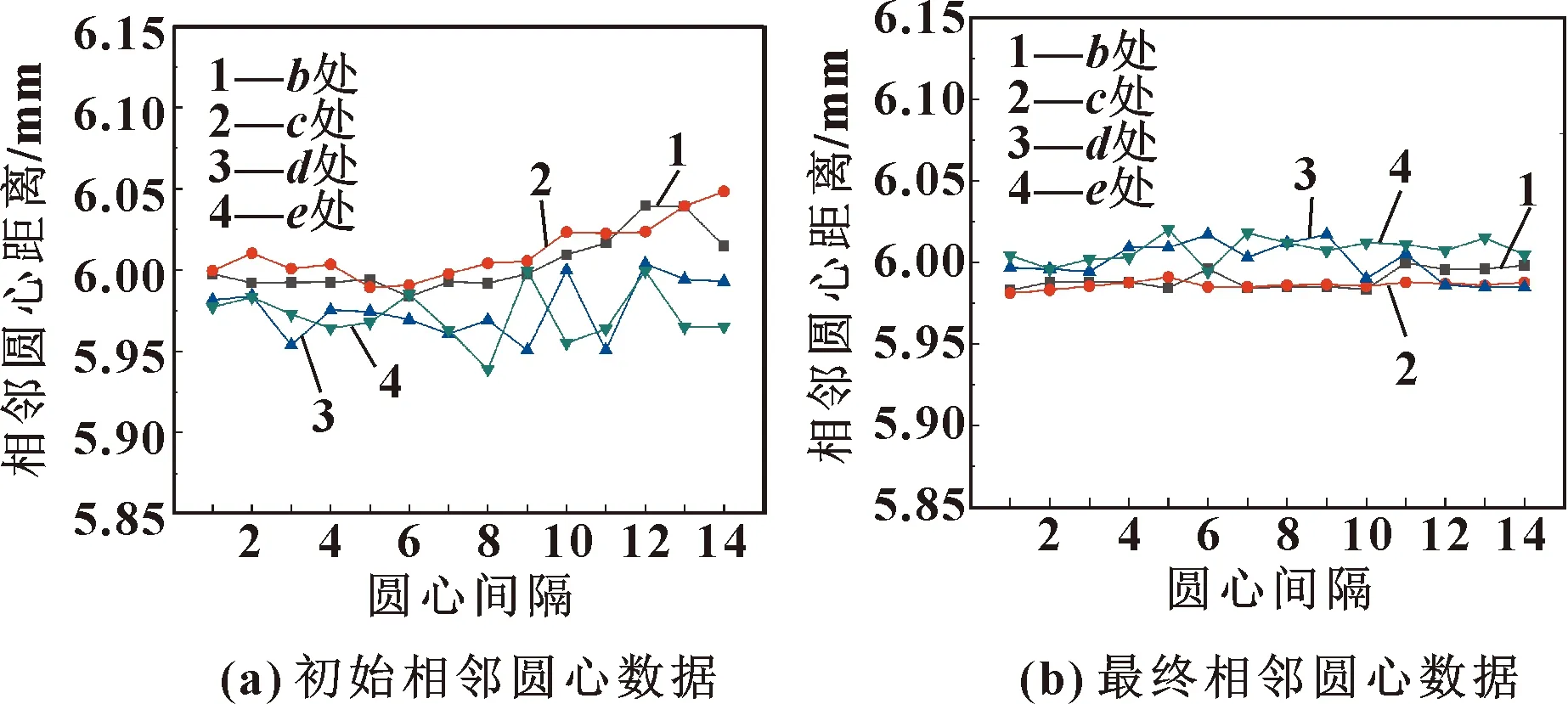
图13 补偿实验结果

4 结论

(1)本文作者针对影像测量中大视场相机畸变校正进行研究，提出一种坐标转换方法。利用棋盘格标定板，以图像中心为原点建立转化坐标系XOY;然后根据公式(4)求出校正完全情况下各交点在转化坐标系中的坐标，再将校正不完全图像中的各交点坐标根据公式(3)转化到坐标系XOY，根据交点一一对应关系建立映射矩阵。

(2)使用映射关系将标定物各圆心坐标转化并再次测量，进行误差补偿；补偿后测量误差均在20 μm以内且在17 μm以内的数据为91.43%，满足影像测量中大视场相机对局部精密区域的测量、检测要求。实验表明：本文作者提出的方法具有一定的重复精度以及误差补偿的可靠性，可有效降低大视场相机校正不完全带来的影响，为研究大视场相机校正提供了参考。