基于RBF神经网络的七自由度凿岩台车钻臂运动学研究*
崔孟豪,姬会福*,惠延波,宋 丹,张中伟
(1.河南工业大学 机电工程学院,河南 郑州 450001;2.中铁工程装备集团有限公司专用设备研究院,河南 郑州 450001)
0 引 言
目前,钻爆法是我国隧道掘进的主要施工方法[1]。凿岩台车是钻爆法施工的核心设备,通过凿岩台车对隧道掌子面进行钻孔作业[2],而钻臂是凿岩台车实现钻孔作业的关键部件[3]。通过对钻臂进行运动学分析,实现对凿岩台车钻孔精准定位,从而完成精确钻孔作业。
为了扩大凿岩台车的工作范围,使钻臂更加灵活,通常将钻臂设计为六自由度及以上的冗余机械臂,而冗余机械臂逆运动学求解是一个难题。
目前,求解机械臂逆运动学的方法有反变换法[4]、几何法[5]、数值法[6]。
覃艳明等人[7]针对八自由度机械臂,根据工作条件对钻臂进行了约束,采用矩阵逆推的方法得到了机械臂多组逆解。KUCUK S等人[8]针对偏置机械臂没有封闭解的问题,提出了一种NIKA的数值解法,能够求解具有超越方程的机器人逆运动学。童水光等人[9]根据位置子矩阵和旋转子矩阵,对满足Pieper准则的六自由度机械臂进行了逆运动学求解,并以ABB机械臂为例,验证了所用方法的有效性;但该方法仅适用于满足Pieper准则的机械臂。葛小川等人[10]采用倍四元数法建立了6R串联机器人的逆运动学方程,求解出了16组解析解,但通过该方法所得逆解不一定能满足全部要求。KOEKER R等人[11]采用神经网络算法(neural-network committee machine, NNCM),得到了六自由度机械臂的逆解。JESUS H等人[12]采用自适应差分进化方法,得到了协作移动机器人的逆运动学。
目前,针对凿岩机械臂逆运动学的研究大多是添加约束,采用解析法。
何清华等人[13]以固定2个移动关节和约束2个关节的方法,确定了爆破孔位外插角的位姿,并采用矩阵逆乘法对九自由度凿岩台车钻臂进行了逆运动学求解;但该方法具有局限性,且其求解过程也较为复杂。王宪伦等人[14]采用几何法,得到了八自由度凿岩钻臂的逆解;但该方法的求解过程复杂,且其求解精度也较低。
为提高凿岩台车钻孔定位精度,减少超欠挖现象,解决钻臂逆运动学求解困难问题,笔者将RBF神经网络算法应用于凿岩台车钻臂逆运动学求解(该算法无需进行矩阵计算,不受钻臂结构和自由度限制),以隧道掌子面真实孔位为例,对RBF神经网络所得逆解精确性进行验证,基于ADAMS-Simulink对钻臂逆解进行进一步联合仿真,以验证逆解可行性。
1 凿岩台车钻臂结构
凿岩台车在工作过程中,需要较大驱动力。而在相同的功率下,液压驱动具有体积小、结构紧凑等的优点,因此,液压驱动方式常常被作为凿岩台车钻臂的优选驱动方式。
七自由度钻臂是目前凿岩台车普遍采用的结构形式。该钻臂的结构模型图如图1所示。
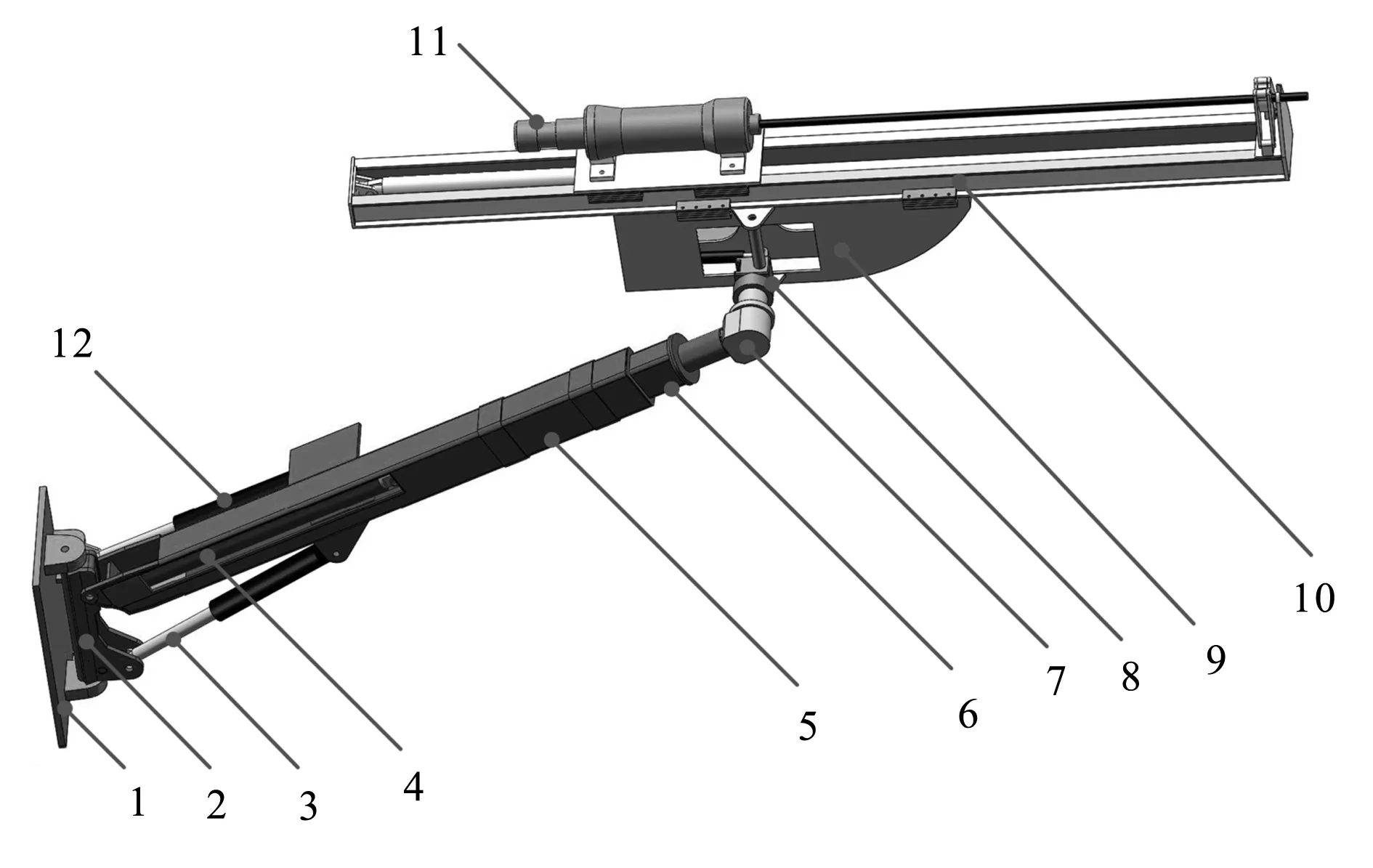
图1 七自由度钻臂结构模型图1—底座;2—摆动关节;3—大臂液压缸;4—伸缩臂液压缸;5—大臂;6—伸缩臂;7—回转关节;8—俯仰补偿关节;9—摆动补偿关节;10—末端移动关节;11—凿岩机;12—摆动液压缸
该钻臂包括2个移动关节和5个转动关节,属于冗余机械臂。
2 凿岩台车钻臂正运动学分析
笔者采用改进D-H法建立钻臂各关节坐标系,并将基坐标系建立在基座上,得到钻臂结构简图和各关节坐标系,如图2所示。
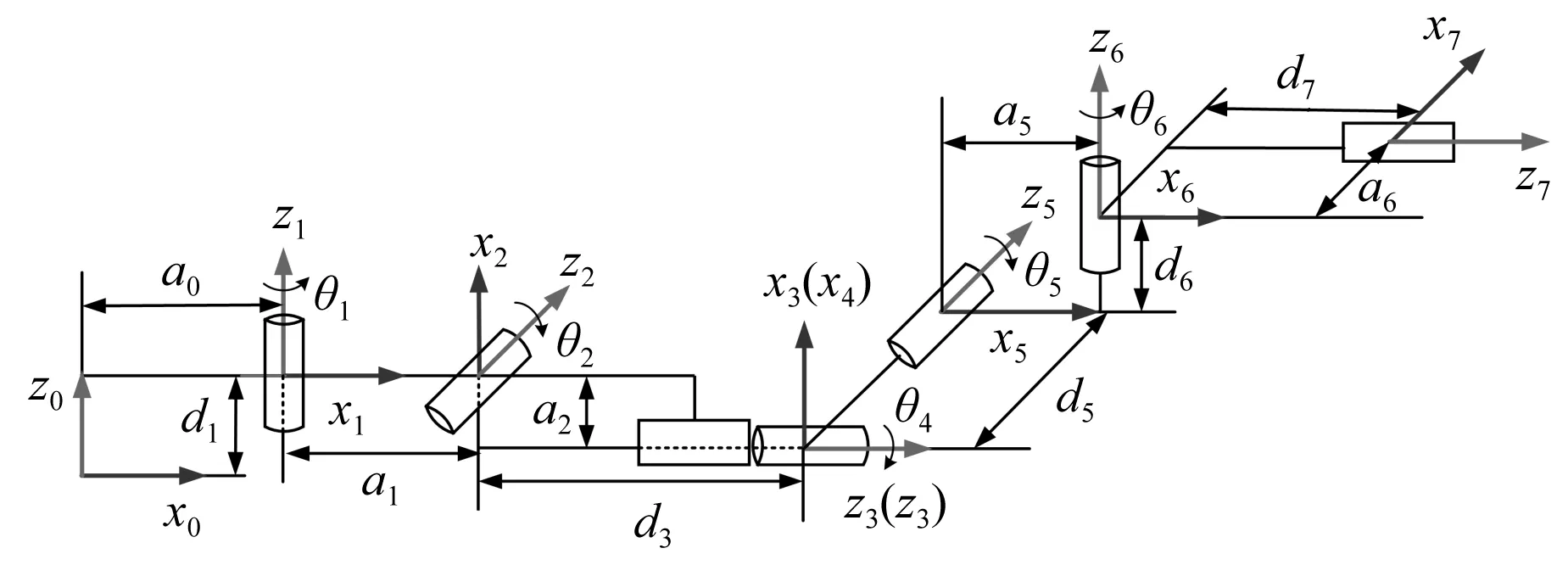
图2 钻臂结构简图和各关节坐标系
该凿岩台车钻臂具有7个关节。
结合钻臂结构相关参数和约束关系,笔者建立各关节D-H参数表,连杆偏距、关节转角、连杆长度、连杆转角分别以a、α、d、θ表示,如表1所示。

表1 七自由度凿岩台车钻臂D-H参数
根据D-H法坐标变换规则,钻臂各相邻关节之间的变换矩阵表达式为:
(1)
结合式(1),可以建立钻臂末端执行器坐标系{7}相对于基座坐标系{0}的位姿矩阵,即为:
(2)
式中:[noa]—钻臂末端相对于基坐标系的姿态;[pxpypz]—钻臂末端相对于基坐标系的位置。
将表1中钻臂各关节变量初始值代入式(2),可得凿岩台车钻臂末端执行器初始位姿矩阵为:
(3)
3 凿岩台车钻臂逆运动学分析
逆运动学是已知机械臂末端相对于基坐标系位姿,反求各关节变量值。笔者以所得钻臂正运动学采集样本数据作为RBF神经网络算法的输入,通过训练预测出钻臂逆运动学,并将逆解代入正运动学矩阵,以验证逆解的有效性。
3.1 RBF神经网络算法设计
钻臂逆运动学是非线性求解过程,RBF可将低维空间非线性不可分问题转换成高维空间线性可分问题,进而实现钻臂的逆运动学精确求解[15]。
RBF神经网络的核心是设计隐含层,为了实现数据由低纬度线性不可分转换为高纬度线性可分,隐含层使用一种高斯函数作为核函数,其激活函数表达式为:
(4)
式中:xp—输出的第P个样本;ci—第i个隐含层的激活函数的中心;σ—函数的宽度参数,即高斯函数的方差;‖xp-ci‖—第P个输入样本到中心点c的距离。
根据所求问题,笔者采用newrbe形式的神经网络,其函数形式表达式为:
[net,tr]=newbe(P,T,spread)
(5)
式中:P—输入样本数据;T—输出样本数据;spread—径向基函数的分布系数。
Newrbe是一种精确径向基神经网络,该函数在创建RBF神经网络时,能够自动选择适合的隐藏层数目,神经元个数自动选择为输入样本个数,使函数拟合更为平滑;为减少逼近误差、提高预测精度和计算速度,只需要设置合理的spread,通过多次仿真,确定spread=1。
3.2 基于RBF神经网络的钻臂逆运动学
在凿岩台车钻孔施工作业过程中,其钻臂末端需要垂直于隧道待掘进面进行钻孔工作。关节7为末端移动关节,仅对钻臂移动距离进行补偿,因此,只需确定前6个关节的姿态,末端关节7在其轴线上根据实际钻孔需求进行移动即可。
故笔者在进行逆运动学分析时,可假设关节7固定,即d7为定值,取其初始值d7=4 022 mm,此时钻臂简化为六自由度,且简化后所得逆解结果不影响凿岩台车实际钻孔作业。
样本数据采集的合适与否直接影响到RBF神经网络的预测精度。笔者通过所得钻臂正运动学方程,利用MATLAB中伪随机数的功能,结合钻臂各关节变量范围,随机生成10 000组各关节变量值,将得到的变量值代入式(2),得到钻臂末端位姿矩阵即输入矩阵为:
(6)
在输出样本矩阵P中,由于只有12个有效数据表示钻臂末端的姿态和位置,为提高预测速度和精度,同时保证求解过程中各关节变量相互独立性,笔者对输入矩阵P进行RPY欧拉角变换,用6个元素来表示钻臂末端的姿态和位置,其结果为:
P1=[α,β,λ,px,py,pz]
(7)
式中:α,β,λ—钻臂末端姿态;px,py,pz—钻臂末端位置。
RPY角欧拉变换方式为:
(8)
所求钻臂逆运动学有6个关节变量,故样本的输出矩阵T为:
T=[θ1,θ2,d3,θ4,θ5,θ6]
(9)
笔者所设计求解钻臂逆运动学的RBF神经网络结构,如图3所示。
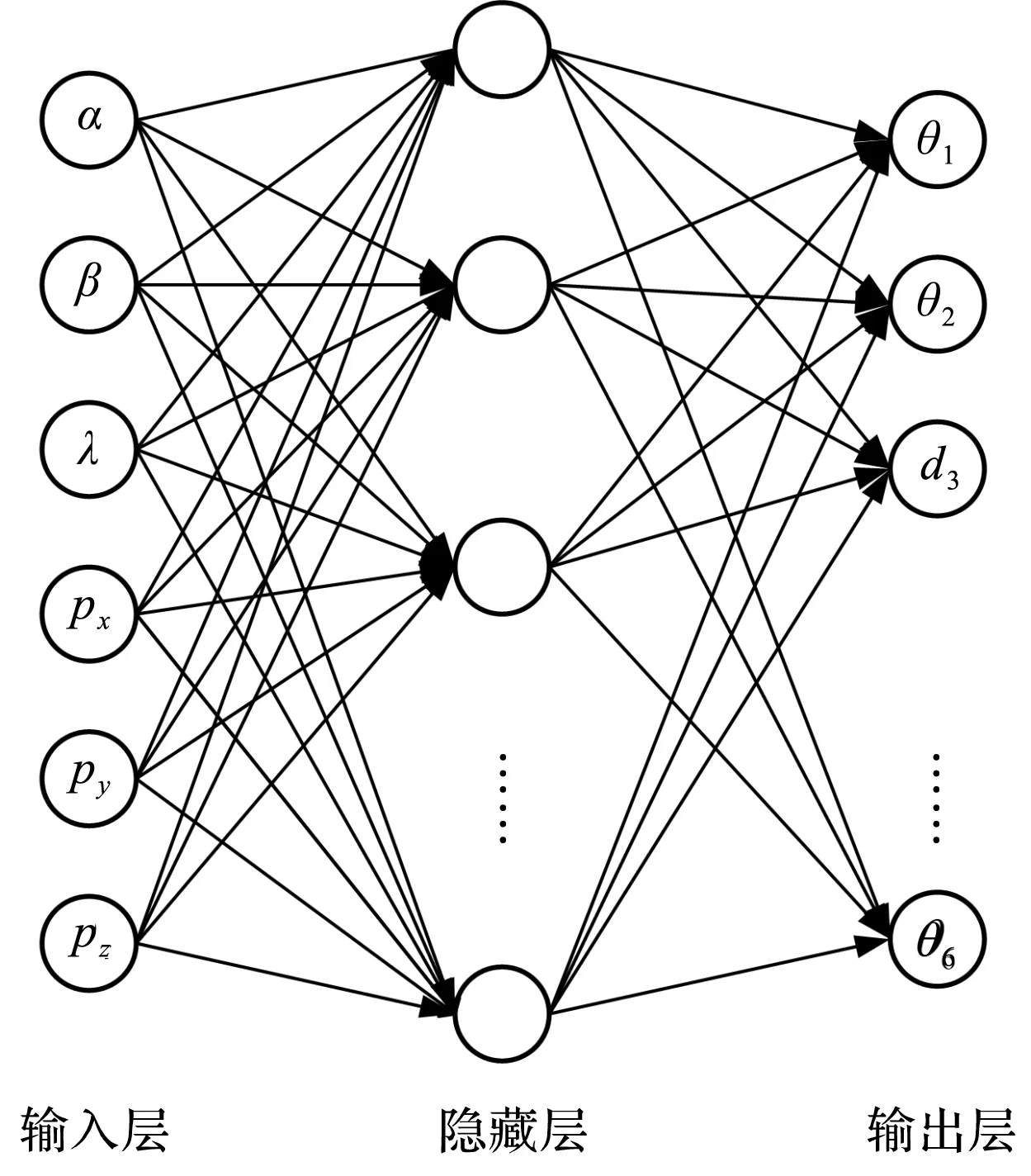
图3 RBF神经网络结构
为避免伪随机数样本中存在奇异值,导致训练时间加长,出现预测结果不收敛等问题,笔者采用最大-最小标准化的归一化方法,对所生成的样本数据进行归一化处理,即:
(10)
式中:Xmax—样本数据中最大值;Xmin—样本数据中最小值。
从所得10 000组数据中,笔者取8 800组数据作为训练数据,1 200组数据作为测试数据,从1 200组预测结果中取部分结果,如表2所示。
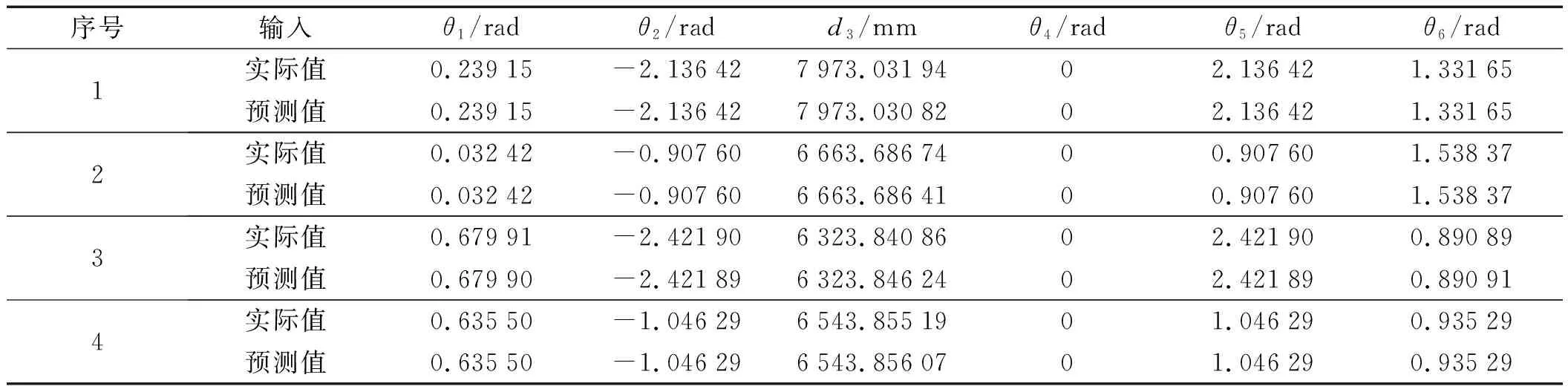
表2 RBF预测结果
由表2可以看出:预测结果误差最大为0.005 38 rad。
笔者进一步建立各关节变量值的预测误差,如图4所示(图中分别表示关节1—6的预测误差)。
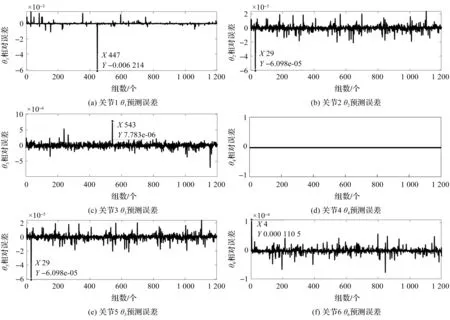
图4 RBF神经网络算法预测误差
由图4可知:
关节1预测最大误差发生在第447组数据,误差值为0.62%;关节2预测最大误差发生在第29组数据,误差值为0.006 1%;关节3预测最大误差发生在第543组数据,误差值为0.000 78%;关节5预测最大误差发生在第29组数据,误差值为0.006 1%;关节6预测最大误差发生在第29组数据,误差值为0.011%。
经过RBF神经网络预测1 200组数据中,各关节中最大误差值为0.62%。由此可以证明,该神经网络结构预测精度较为精确。
其中,关节4预测误差图4(d)中,由于约束钻臂垂直隧道掌子面,关节4的变量值保持初始值不变,经过RBF预测输出值没有误差。
3.3 钻臂预测孔位误差分析
为验证RBF神经网络所得钻臂求逆运动学结果准确性,笔者以隧道掌子面所布63个孔位为例,凿岩台车到隧道掌子面距离为9 m(每个孔位位姿已知),得到隧道孔位横截面分布图,如图5所示。
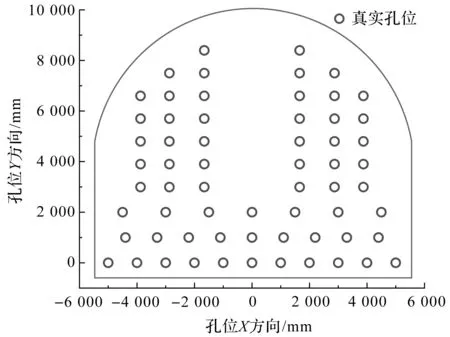
图5 隧道掌子面布孔图
笔者将隧道掌子面63个孔位位姿数据输入到上文经过训练的RBF神经网络中,基于RBF神经网络求解钻臂得到对应孔位时各关节变量值。
对比分析基于数值法获得的钻臂各关节变量值,如表3所示。
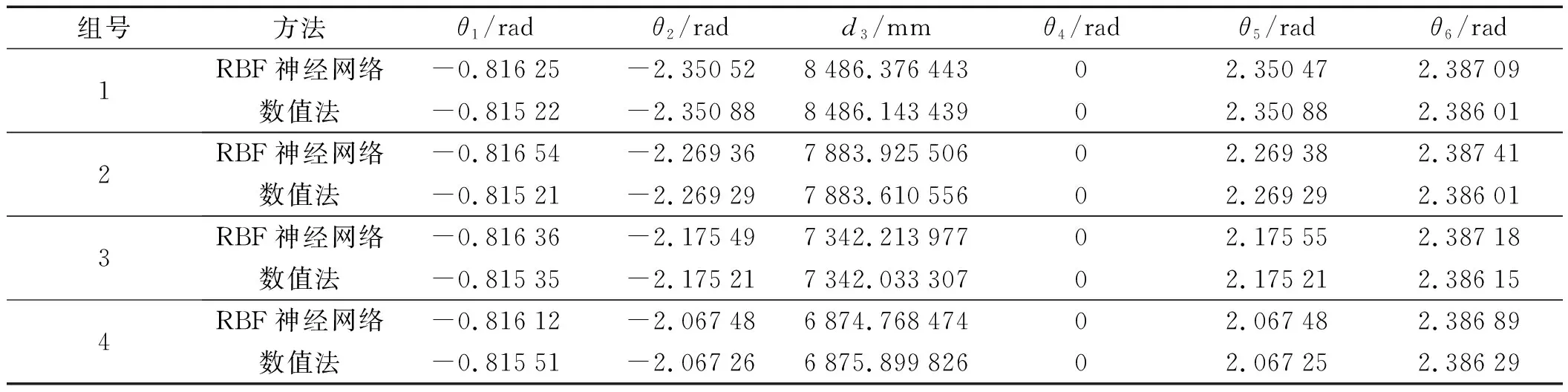
表3 不同方法所得逆解结果
由于钻臂达到每个孔位时,各关节变量值的实际值是未知的,因此,为验证所得钻臂逆解结果的准确性,笔者将RBF神经网络和数值法所得各个关节变量值代入钻臂末端位姿矩阵公式,得到钻臂末端执行器位姿,并将所得位姿与隧道掌子面对应孔位位姿进行对比,结果如图6所示。
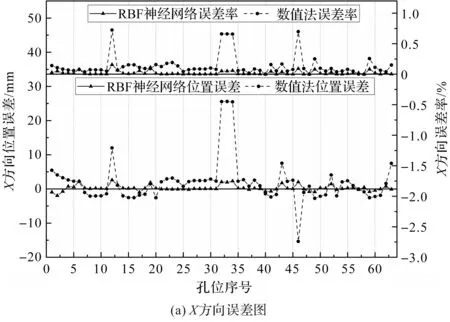
从图6中可看出:基于RBF神经网络预测孔位误差整体低于数值法所得结果。其中,在X方向上,RBF预测孔位最大误差为2.588 mm,误差率最大为0.156%,数值法所得孔位最大误差为25.589 mm,误差率最大为0.724%;Y方向上,RBF神经网络预测孔位最大误差为2.336 mm,误差率最大为0.096%,数值法所得孔位最大误差为10.611 mm,误差率最大为0.282%;
且RBF神经网络所预测63个孔位结果的X、Y方向上平均误差分别为0.591 mm、0.465 mm,数值法所得63个孔位结果的X、Y方向上平均误差分别为3.592 mm、1.168 mm;
RBF神经网络预测结果所得63个孔位,X、Y方向误差超过1 mm的仅有17个孔位,而通过数值法所得63个孔位中,X、Y轴方向误差超过1 mm的有62个。
由此可知,RBF神经网络算法所预测孔位整体精度高于数值法所得孔位,且所预测孔位误差在钻孔施工范围内。
3.4 钻臂运动学虚拟现实仿真分析
为验证所提出运动学方法应用于凿岩台车钻臂的可行性,基于ADAMS-Simulink,笔者对钻臂三维模型模拟钻孔定位过程进行联合仿真。
仿真环境中添加有重力,并对钻臂各关节设置材料属性,以模拟实际钻孔定位过程,进一步验证所得逆运动学可行性。限于篇幅,笔者取部分孔位进行钻孔验证。
钻臂运动学虚拟联合仿真结果,如图7所示。

图7 虚拟联合仿真模型
图7中,笔者首先将钻臂模型导入ADAMS,根据逆解结果及钻臂施工特点添加约束和驱动;然后在Simulink模型中,建立钻臂各关节运动模型,采用模糊PID控制算法搭建钻臂控制系统,实现对钻臂钻孔定位的控制;最后,将钻臂各关节轨迹规划结果作为Simulink中输入,由此进行ADAMS-Simulink联合仿真。
通过在ADAMS钻臂模型末端建立Mark点,笔者测量了其相对于基坐标系的位置坐标。
联合仿真结果如表4所示。
通过表4可以看出:联合仿真孔位与RBF神经网络预测孔位最大误差为第3组仿真孔位,X、Y方向误差值分别为0.9 mm、1.39 mm。
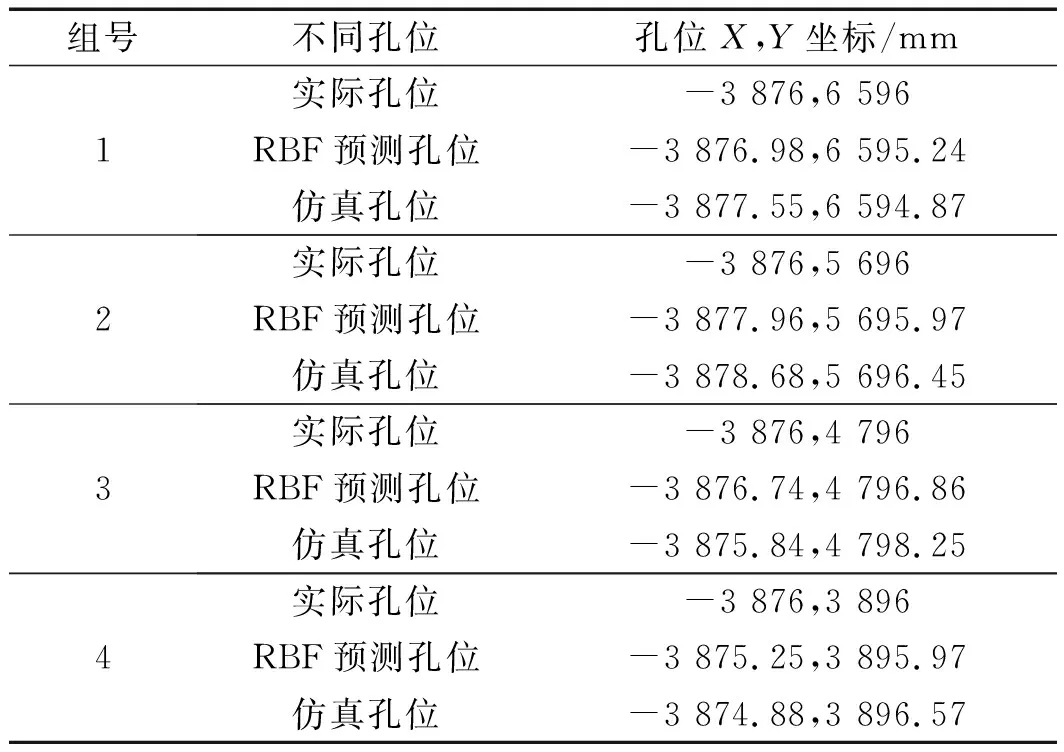
表4 联合仿真结果对比
这是由于ADAMS为钻臂实物模拟仿真,仿真环境中添加有重力等因素,使得仿真结果与理论求解值存在一定误差,但钻臂末端依然垂直于隧道断面,且该误差在钻孔施工允许的范围内,不会因此造成隧道掘进面超欠挖现象,由此可知,所求孔位对应的逆解是可行的。
4 结束语
为了提高凿岩台车钻孔定位精度,首先,笔者对七自由度凿岩台车钻臂运动学进行了研究,采用RBF神经网络求其逆运动学;然后,以隧道孔位进行了验证;最后,采用ADAMS-Simulink对钻孔定位进行了联合仿真。
研究结果表明:
(1)针对不满足Pieper准则的七自由度凿岩台车钻臂逆运动学没有封闭解,笔者采用了RBF神经网络算法求解钻臂逆解。根据凿岩台车钻孔时要求钻臂垂直隧道掌子面的要求,结合钻臂结构建立钻臂运动约束条件,通过RBF神经网络求解了钻臂逆运动学,仿真结果表明其最大预测误差为0.62%;
(2)为验证求逆解有效性,笔者以隧道掌子面所布63个真实孔位为例,采用RBF神经网络求出了每个孔位对应的一组逆解,通过正运动学得到了逆解对应的孔位位姿,同时采用数值法求解了所有孔位位姿。笔者将两种方法所得孔位位姿与真实孔位位姿进行了对比,结果表明,RBF神经网络所得孔位位姿误差低于数值法,X、Y方向最大误差分别为2.588 mm、2.336 mm;
(3)笔者基于ADAMS-Simulink对钻孔施工进行了联合仿真验证,仿真结果误差在施工允许范围内,由此验证了逆解可行性,能够提高钻孔定位精度,使凿岩台车减少因定位误差产生超欠挖现象,满足钻孔施工要求。
笔者后续将针对X、Y方向误差相差较大问题开展进一步的研究,并以凿岩台车样机为例进行实际钻孔实验,对实际钻孔时钻臂定位所产生误差的原因进行分析。

