楔横轧上料机器人设计与分析*

郭 凯,张 静*,寇子明,郭宏伟,夏 峰,单天松

(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.山西省矿山流体控制工程技术研究中心,山西 太原 030024;3.矿山流体控制国家地方联合工程实验室,山西 太原 030024;4.哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨 150006;5.青岛海德马克智能装备有限公司,山东 青岛 266111)

0 引 言

在超大型轴类零件轧制生产过程中,楔横轧机的上料多由人工完成,存在危险性高、工作任务繁重、自动化程度低的问题,严重影响了超大型轴类零件的轧制效率[1,2]。

作为一种多学科融合的高新技术设备,重载上料机器人可有效解决以上问题,且随着科技进步和市场发展需要,其已成为不可或缺的自动化重载上料工具[3,4]。因此,研究者们以楔横轧领域应用为背景,面向超大型轴类零件等重型构件的自动化转运需求,立足于机器人工作空间、抓取灵活性以及稳定性的提升,以机器人本体构型设计为牵引,开展了对重载上料机器人的研制工作[5,6]。

舒阳[7]设计的重载码垛机器人与CHU A M等人[8]设计的锻件转运机器人均采用混联式机构,具有体积小、重量轻、关节数量少等特点;但机器人所受倾覆力矩大、结构强度较低、稳定性较差。李阁强等人[9]基于平行四连杆机构设计的全液压重载锻造转运机器人,与李跃等人[10]采用缓冲装置与铰链式四连杆机构相结合设计的码垛重载机器人,均有转运速度快、定位精度高、承载能力大等优点;然而两者夹持物料时存在偏载严重、本体占用空间大、运动空间较小的问题,不适用于工作空间受限的区域。武广平[11]研制的四平行四连杆式重载转运机器人,与魏雅君等人[12]设计的结合响应面法和拓扑法进行结构优化后的MP-MD110型重载码垛机器人具有轻量化、高刚度、高负载、控制简单的特点;但两者的末端执行器均存在动作不灵活的缺陷,不便于其位置的调整。徐振邦等人[13]基于改进型蒙特卡洛法,精确求解了九自由度超冗余串联机械臂的工作空间。贾磊等人[14]采用ADAMS对重载码垛机器人进行了动力学仿真,得到了其设计参数。

针对以上重载上料机器人存在的问题及优势,为匹配智能化超大型轴类楔横轧设备,笔者提出一种新型楔横轧上料机器人。

首先,笔者基于六连杆机构和四连杆机构进行机器人本体机构设计,实现机身升降、大臂摆动等动作;同时,进行夹钳的夹取和回转机构设计。结合大尺寸轴类零件的转运需求,依次建立机器人各组件的三维模型,并通过D-H法建立机器人连杆坐标系,对机器人进行正逆运动学分析,基于MATLAB求解得到其工作空间;利用ADAMS对机器人虚拟样机进行动力学分析,得到其所有驱动部件的受力和力矩变化曲线,以及关键杆件上各铰接点的受力变化曲线,并分析其各曲线的变化原因。

1 机器人设计原理

1.1 机器人整体机构设计

上料机器人整体机构主要由基于六连杆机构ADEFC的升降机构与基于四连杆机构GHIJ的大臂摆动组件串联构成。

机器人整体机构简图如图1所示。

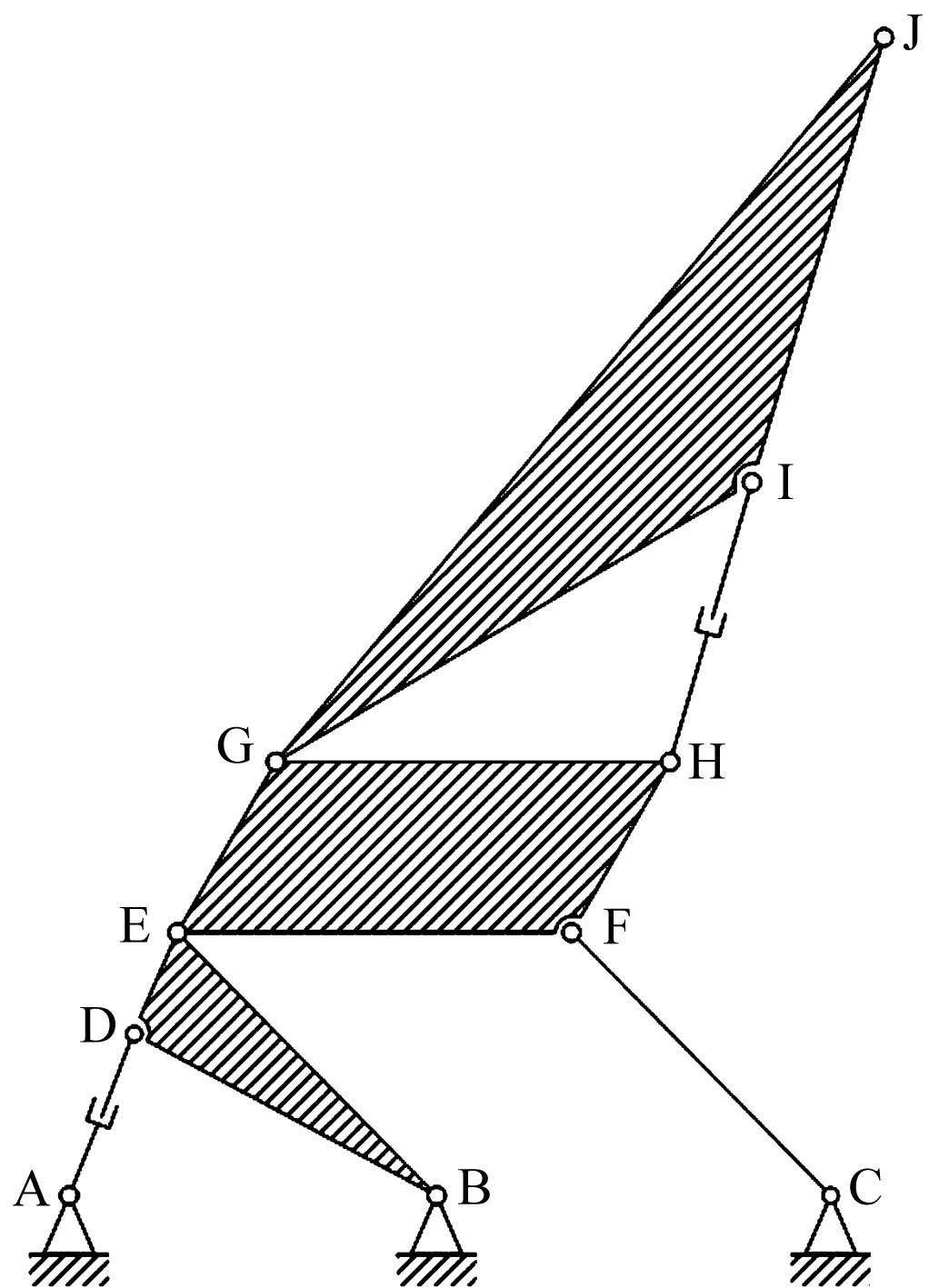
图1 机器人机构简图

图1中,夹钳在升降机构与大臂摆动组件的作用下实现大范围平动,同时绕J点转动。

1.2 升降机构设计原理

在机器人转运物料时,为了满足其竖直升降的要求,以及机身在转运过程中保持稳定姿态的要求,笔者基于六连杆机构设计了升降机构。

笔者将图1中D、E两点的转动副合并为连接滑杆、主动杆及升降连杆的复合铰链,可得升降机构原理简图,如图2所示。

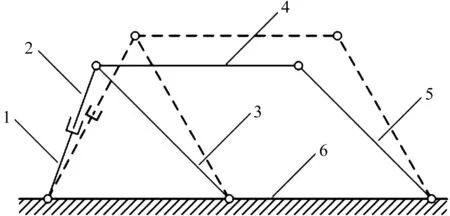
图2 升降机构原理简图1—导杆;2—滑杆;3—主动杆;4—升降连杆;5—摆杆;6—机架

图2中,该六连杆机构由两个四连杆机构串联组成:导杆、滑杆、主动杆及机架构成一个四连杆机构;导杆与滑杆通过移动副连接组成一个直线驱动单元,可使主动杆绕机架转动。主动杆、升降连杆、摆杆及机架构成一个平行四边形连杆机构。主动杆绕机架转动,利用平行四边形对边保持平行的性质,驱动升降连杆始终做与机架保持平行的升降运动,不仅拓展了机器人的升降空间,而且达到了升降平稳的目标。

1.3 大臂摆动组件设计原理

在转运轴类零件时,为了实现机器人左右位置变化及二次升降,笔者基于四连杆机构设计了大臂摆动组件,其原理简图如图3所示。

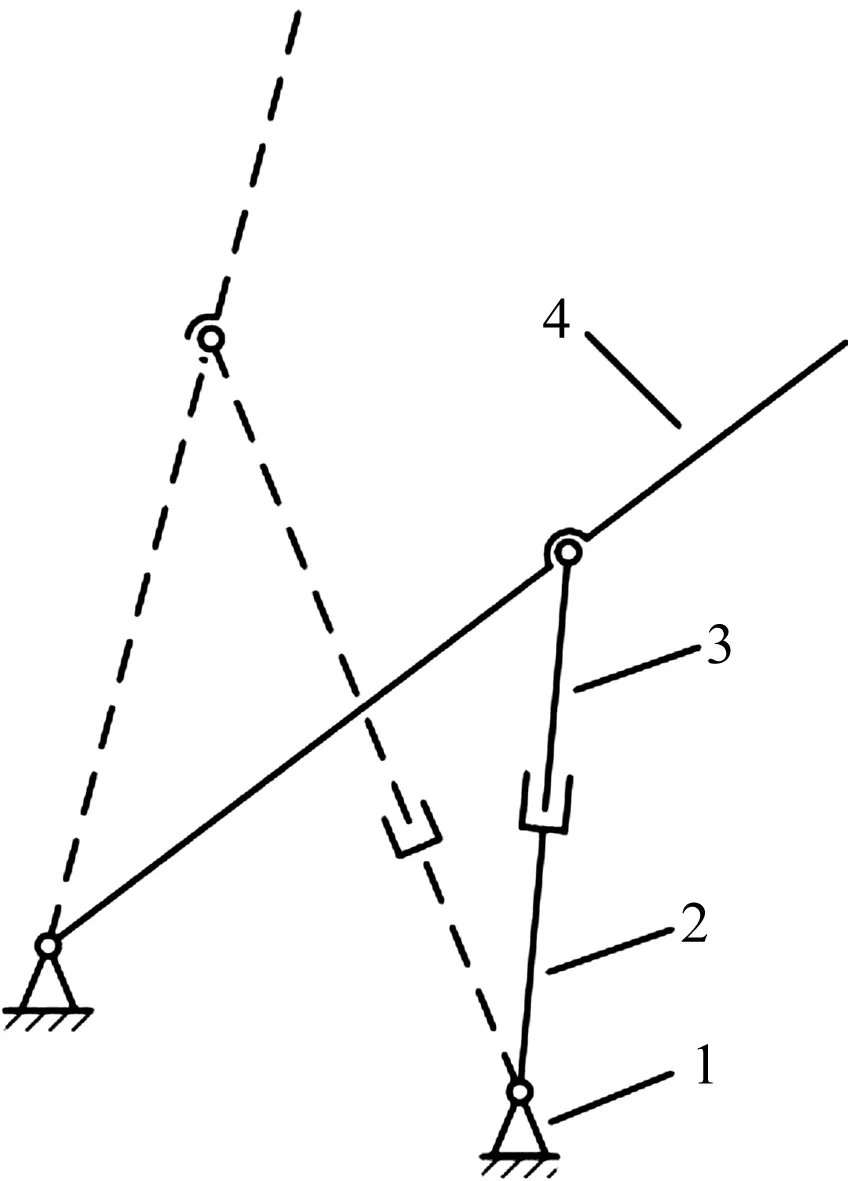
图3 大臂摆动组件原理简图1—摆臂底座;2—支撑套;3—支撑杆;4—大臂连杆

图3中,该四连杆机构由摆臂底座、支撑套、支撑杆及大臂连杆组成。其中,支撑套底部与大臂连杆底部分别铰接于摆臂底座的不同位置。支撑杆与支撑套间的相对移动构成了一个直线驱动单元,驱动大臂连杆绕摆臂底座摆动,实现物料的左右转移。

同时,笔者利用四连杆机构放大驱动单元行程,实现了机器人二次升降,进一步拓展了机器人的工作空间。

1.4 夹钳设计原理

为使机器人能实现灵活抓取,笔者设计了一种可翻转的自动夹钳。该夹钳由钳头部分和翻钳部分组成。其中,翻钳部分是一个回转装置,将钳头部分固定安装于翻钳部分,构成一个可翻转自动夹钳,相较于传统夹钳具有很高的灵活性。

该处利用拉紧机构实现钳头部分的抓取动作,其工作原理简图如图4所示。

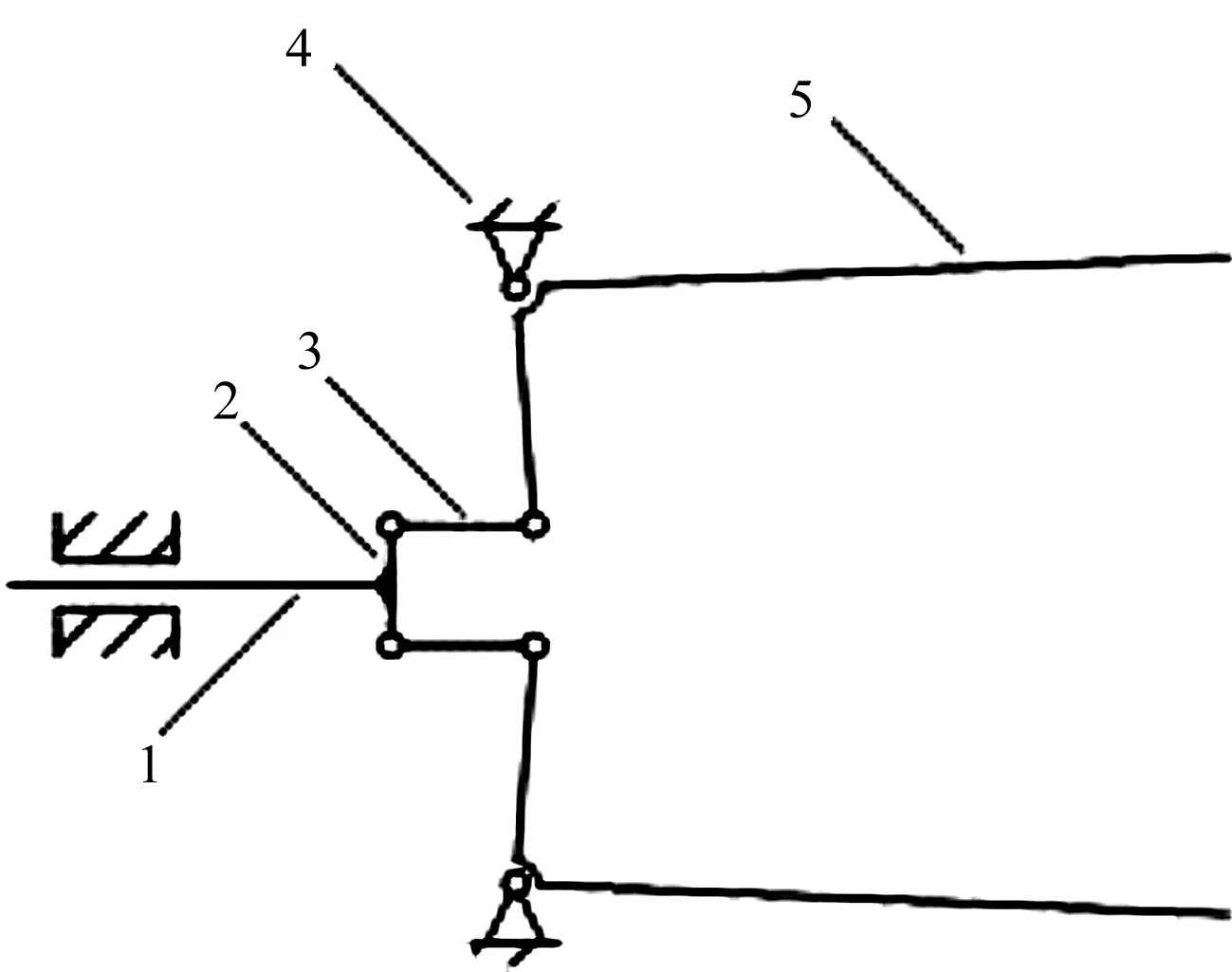
图4 钳头部分工作原理简图1—拉杆;2—拉块;3—拉板;4—钳头体;5—钳臂

由图4可知:拉杆一头连接驱动部件,另一头与拉块固定连接,做往复直线运动。拉块又分别与上下对称的两拉板铰接,两拉板分别与上下对称的两钳臂铰接,两钳臂另一端又铰接于钳头体上。

当拉杆在驱动力的作用下向左运动时,通过拉块及拉板带动上下钳臂分别绕着固定支点做顺(逆)时针转动,完成夹钳闭合抓取动作。反之,则完成夹钳张开放置动作。

1.5 机器人机构自由度计算

根据平面机构自由度计算公式[15],笔者求解图1中机器人机构自由度:

F=3×(N-1)-2PL

(1)

式中:F—机构自由度;N—机构构件总数,N=9;PL—机构低副总数,PL=11。

由式(1)可得机器人机构自由度为:F=2。

图1是四自由度机器人去除末端夹钳翻转与夹取两个自由度后所得,因此,由自由度计算结果可知其设计满足机器人动作要求。

2 机器人结构

楔横轧上料机器人需转运的轴类零件直径约为250 mm,质量为800 kg。笔者据此对机器人的具体结构进行设计。

2.1 升降组件结构

升降组件是由一组升降机构对称布置于升降部分底座构成。并联布置的方式可使机器人负载分配均匀合理,提高了其升降的稳定性,减少了其对地面的冲击。

双油缸的驱动方式使机器人的承载能力得到了很大提升,其所构成的升降组件如图5所示。

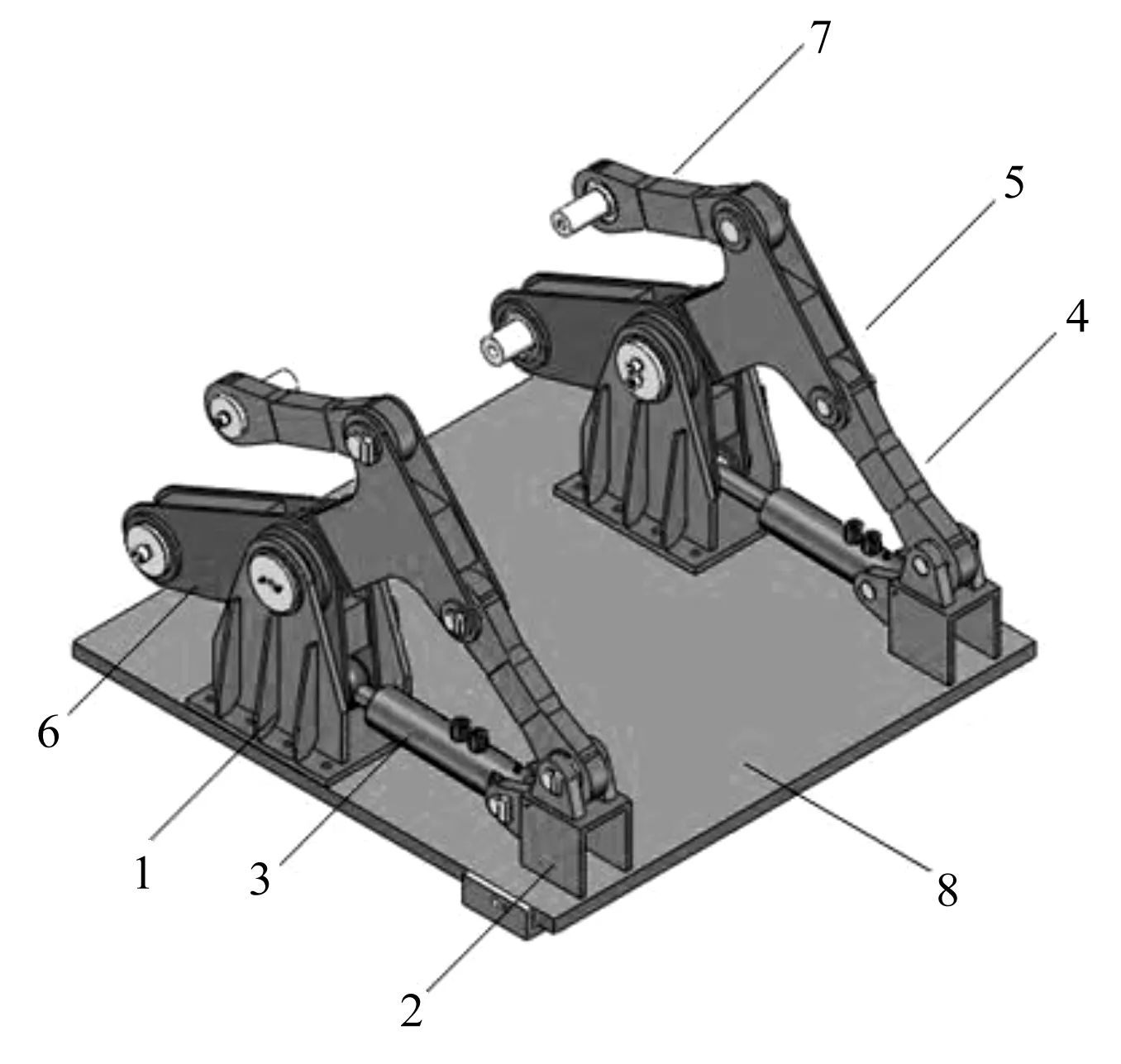
图5 升降组件三维模型1—连杆支座;2—升降油缸支座;3—升降油缸;4—固定连杆;5—“T”型杆;6—主动杆;7—摆杆;8—升降部分底座

图5中:由于液压驱动易获得较大的力和力矩,可实现快速且无冲击的升降[16],因此,此处升降机构中的直线驱动单元由升降油缸代替。机架则是一个由连杆支座、升降油缸支座、固定连杆与“T”型杆组成的三杆机构。固定连杆一端与升降油缸支座相连,另一端与“T”型杆相连。“T”型杆一端与摆杆相连,另一端则是通过连杆支座的销轴和主动杆连接。主动杆是“L”型杆,其可将升降油缸近似水平的直线往复运动转化为升降连杆的上下运动。

2.2 大臂摆动组件结构

根据图3,笔者对大臂摆动组件各构件进行具体结构设计,同样将直线驱动单元由摆动油缸代替,得到大臂摆动组件的三维模型,如图6所示。

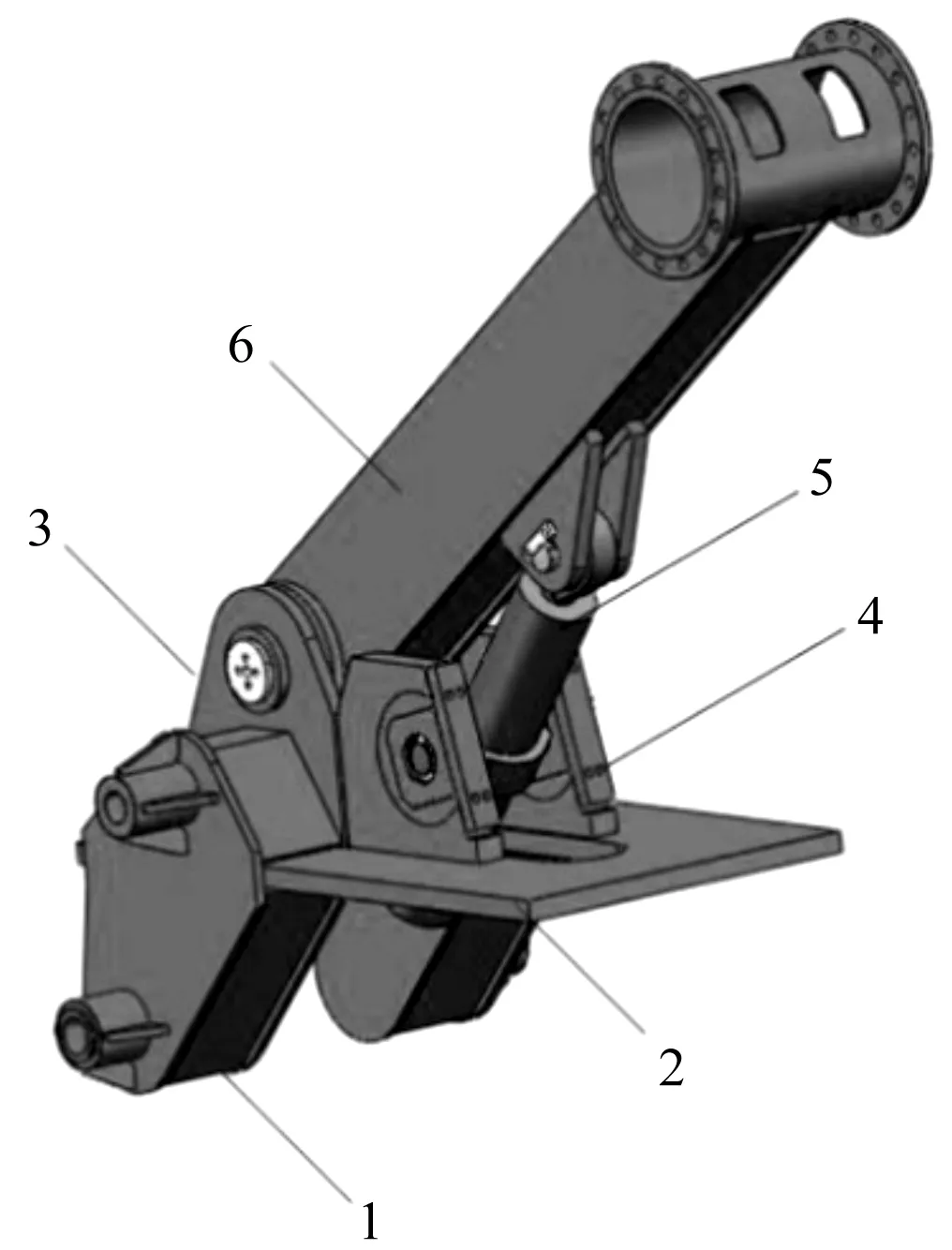
图6 大臂摆动组件三维模型1—升降连杆;2—摆臂底板;3—大臂连杆支座;4—摆动油缸支座;5—摆动油缸;6—大臂连杆

在图6中,一组并联的升降连杆与摆臂底板、大臂连杆支座,以及摆动油缸支座构成摆臂底座;升降连杆为筒式结构,摆臂底板水平嵌入到升降连杆中,在升降连杆的带动下,摆臂底板始终平行于地面升降,以保证升降过程的稳定性及准确性;摆动油缸以及大臂连杆均与各自支座铰接,摆动油缸布置在大臂连杆的下方,驱动大臂连杆绕其支座摆动。

2.3 夹钳结构

基于图4的夹钳设计原理,笔者研制了机器人末端夹钳结构,如图7所示。

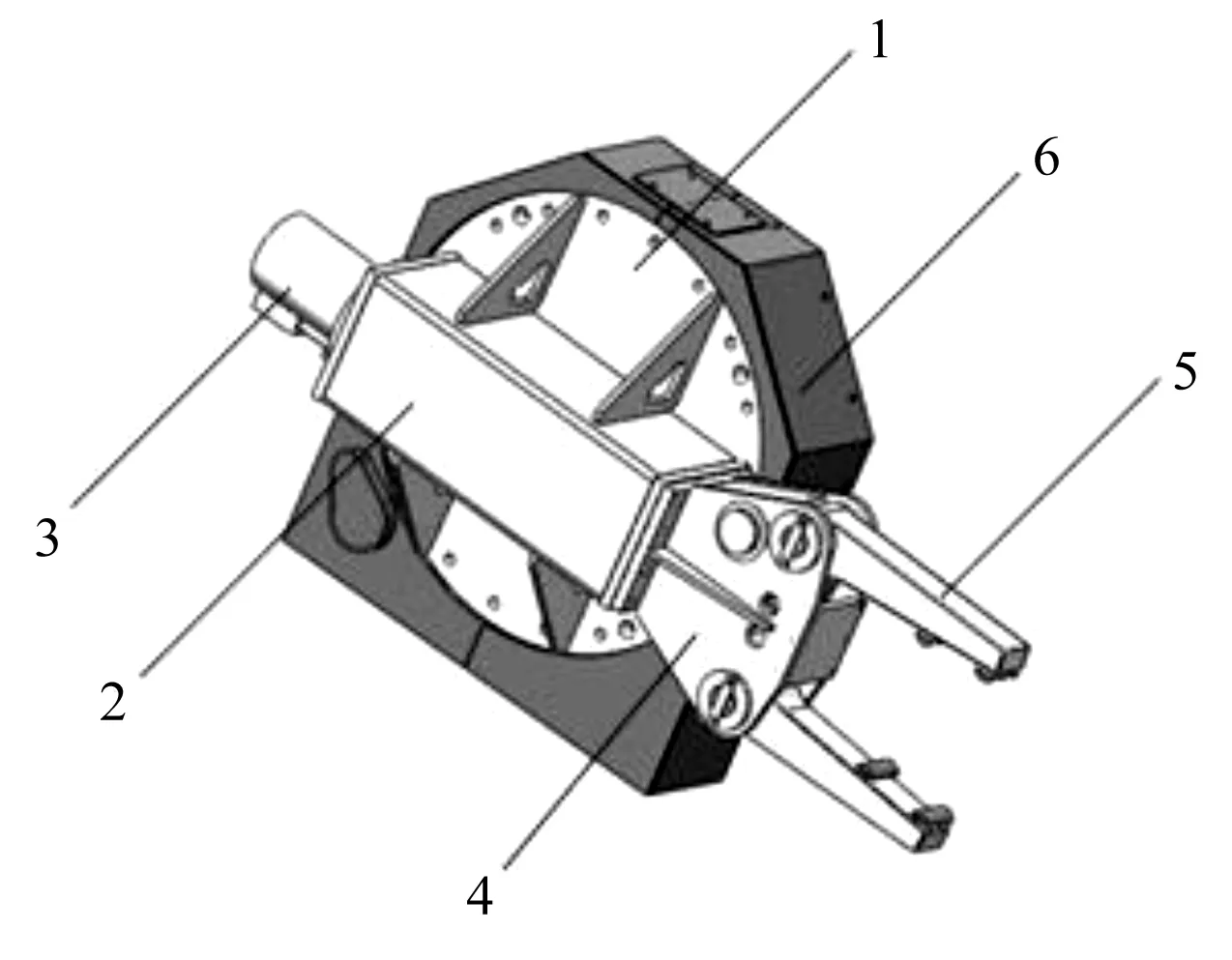
图7 夹钳三维模型1—法兰板;2—方筒;3—夹紧油缸;4—钳头体;5—钳臂;6—翻钳部分

在图7中:钳头部分的方筒固定在法兰板的外表面,方筒左侧固定有夹紧油缸,右侧安装有钳头体,拉杆穿过方筒与夹紧油缸活塞杆连接,随着活塞杆的往复直线运动,带动夹钳夹紧张开;

翻钳部分的回转功能由内置电机与齿轮减速器实现;钳头部分通过法兰板与翻钳部分的回转端面相连,构成可翻转的自动夹钳。

2.4 机器人整体结构

笔者将大臂摆动组件中的升降连杆与升降组件中的对应杆件连接,同时将夹钳对称置于大臂连杆头部两侧,即可得到楔横轧上料机器人的虚拟样机模型如图8所示。

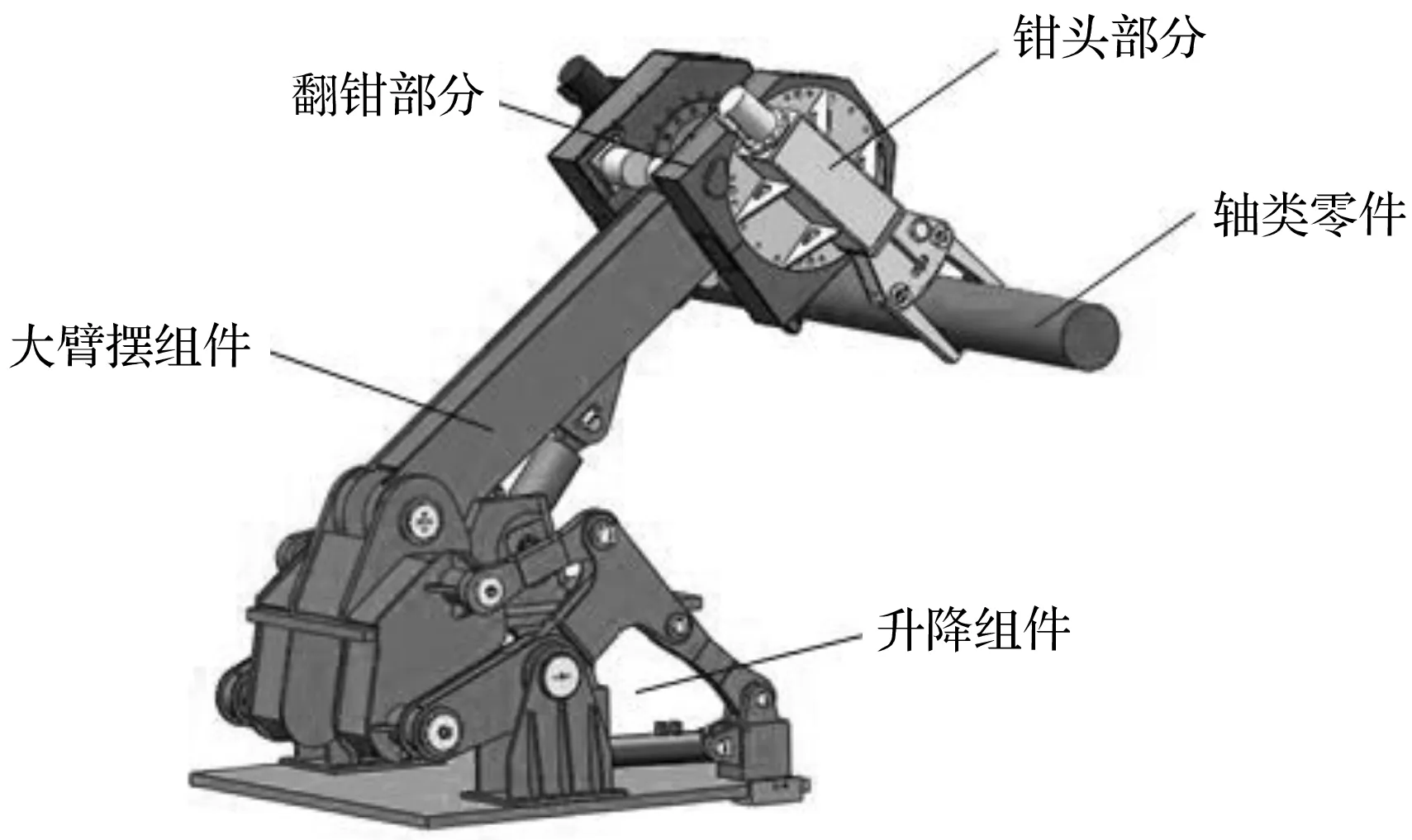
图8 上料机器人三维模型

图8中,升降组件实现机身的稳定升降,大臂摆动组件实现轴类零件左、右转移以及二次升降,两者构造了符合任务要求所需的工作空间大、升降稳定、高负载的混联式机器人主体;搭载可翻转的自动夹钳,保证了机器人夹取的灵活性,夹钳采用对称布置的方式避免了单侧夹取时偏载严重的情况,减少了机器人在非受力方向的变形。

3 机器人运动学分析

3.1 D-H坐标系构建

标准型D-H参数法[17,18]通过连杆转角θi、连杆距离di、连杆长度ai和连杆扭角αi等4个独立参数,确定机器人各杆件参数及关节变量。

由于D-H法不能直接用于混联机构,且机器人机构中存在移动副,以及多个四连杆机构,为方便建立D-H坐标系,笔者将图1机器人整体机构简化为只含转动副的串联机器人机构,并将其运动形式简化为单连杆绕定轴转动。

笔者以BE为连杆1、EG为连杆2、GJ为连杆3,以B点为初始坐标系原点,分别在4个旋转关节B、E、G、J处建立坐标系。

最后得到的标注有D-H坐标系的机构简图,如图9所示。

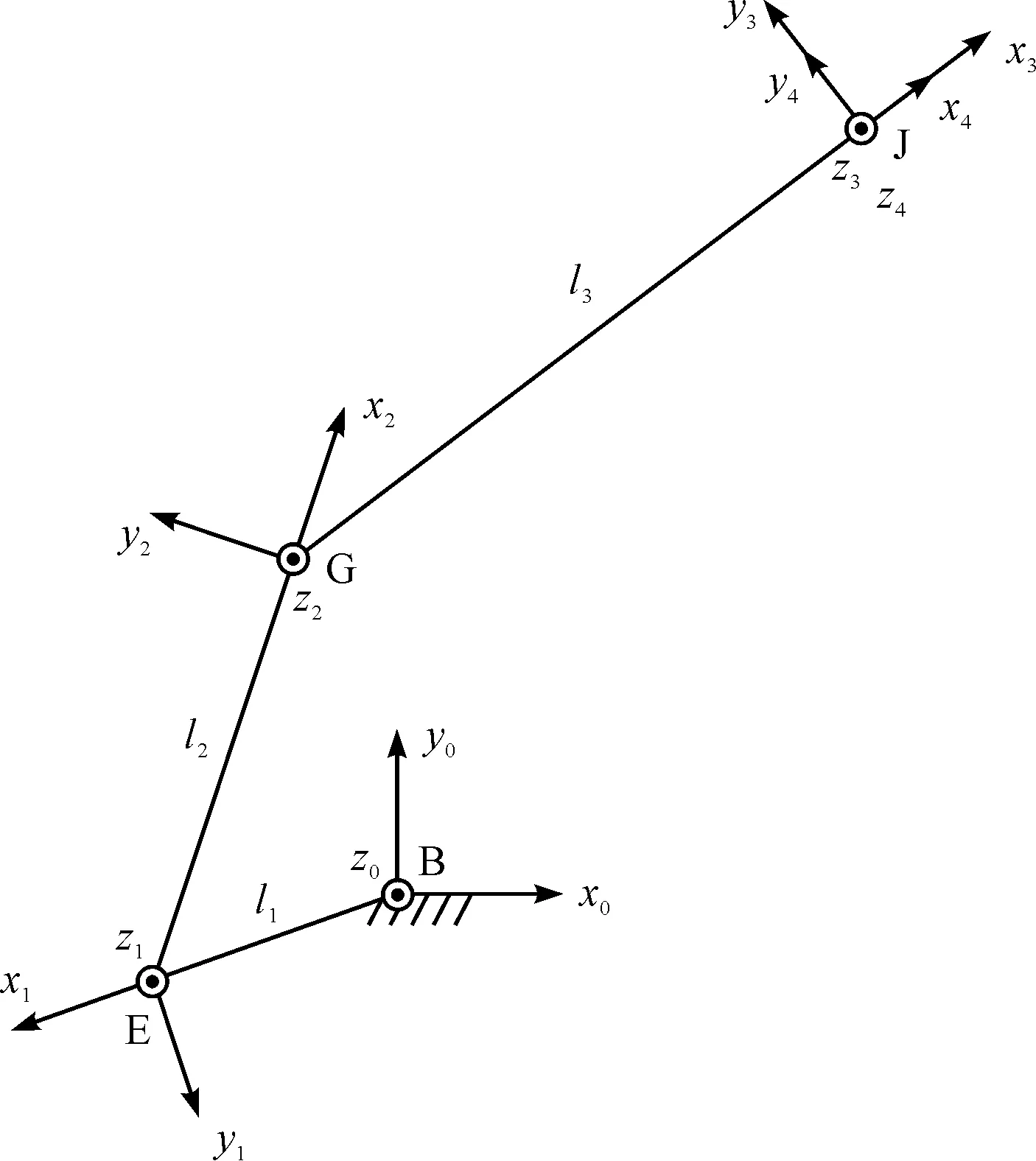
图9 上料机器人机构简化图

根据图9列出相应的D-H参数表,如表1所示。

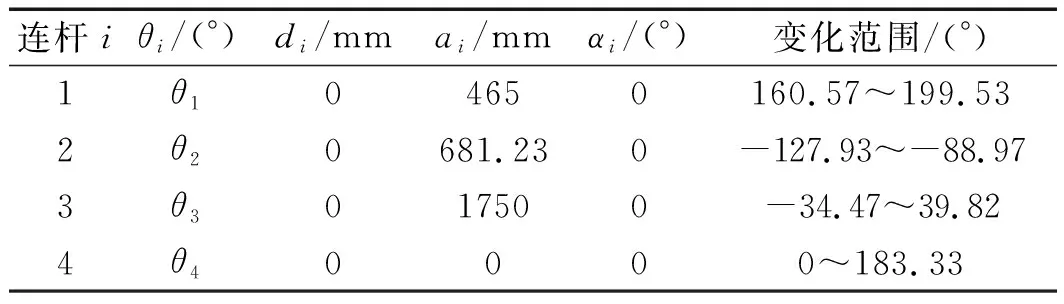
表1 上料机器人D-H参数

表1中,θ1、θ3、θ4是主动变量,θ2是相关变量,且θ1+θ2=71.6°。

3.2 机器人正运动学分析

机器人正运动学分析为:已知各杆件结构参数以及关节变量,求解末端夹钳在操作空间中的位置与姿态。

相邻坐标系间的位姿变换矩阵可表示为:

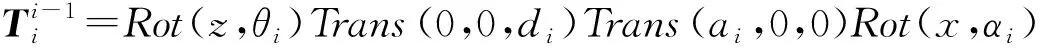
(2)

式中:i—连杆。

当i=0时,表示基坐标系。

笔者将D-H参数表中的参数分别代入式(2)中,可得到所有相邻坐标系间的齐次坐标变换矩阵:

(3)

(4)

(5)

(6)

式(3～6)中:si—sinθi的缩写;ci—cosθi的缩写;下同。

将以上矩阵依次相乘,可得到机器人末端夹钳相对于基坐标系的位姿变换矩阵:

(7)

式中:sijk—sin(θi+θj+θk)的缩写;cijk—cos(θi+θj+θk)的缩写(下同)。

在基坐标系下,末端夹钳的位置矢量与方向矢量所组成的4×4矩阵如下:

(8)

由式(7，8)相等,可得正运动求解结果为:

3.3 机器人逆运动学分析

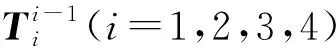
(1)求解关节角度θ1。

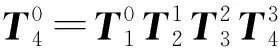
(9)

式(9)两边展开,并化简,令两侧矩阵(1,3)和(2,3)位置的元素相等,可求得:

θ1=arctan2(ay,ax)或θ1=arctan2(-ax,ay)

(10)

(2)求解关节角度θ2。

由于设计时已知θ1+θ2=71.6°,所以有:

θ2=71.6°-θ1

(11)

(3)求解关节角度θ3。

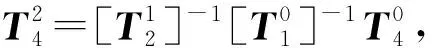
θ3=arctan2(k2,k1)

(12)

其中:

k1=(pxc12+pys12-a2-a1c2)/a3
k2=(pyc12-pxs12+a1s2)/a3。

(4)求解关节角度θ4。

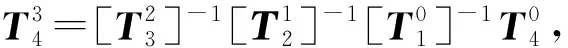
θ4=arctan2(nyc123-nxs123,nxc123+nys123)

(13)

由上述推导可知,机器人的运动学逆解具有多重性,这是由于表达式的不唯一性和求解反三角函数方程式造成的。在选取各关节角度时,首先依据关节角度变化区间确定θ1的值并以此为参考,然后将所得结果代入到各角度的代数表达式,依次求出θ2、θ3和θ4的值,检查所得角度值是否在设定的区间内,以避免各连杆在运动时发生干涉且保证运动连续性,最后获得一组最优解。

3.4 机器人工作空间分析

机器人的工作空间范围可有效表征其运动特性,用来验证机器人轨迹规划的正确性,对机器人辅助优化有着重要意义[20,21]。

笔者首先依据图9中D-H坐标系及表1中D-H参数,在Robotics Toolbox中建立机器人在初始位置时的运动仿真模型,然后对其做工作空间分析。

机器人在初始位置时的运动仿真模型如图10所示。

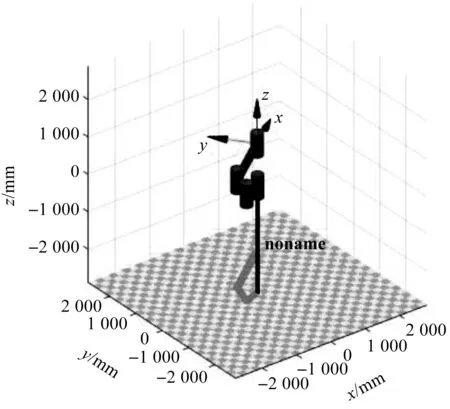
图10 基于MATLAB机器人运动模型

基于蒙特卡洛法,利用MATLAB中的Rand函数,笔者同时从4个旋转关节变量的范围内随机取值,将得到的4个随机值代入到正运动学求解所得的末端夹钳位姿表达式中,即可确定一个工作点位。

利用for函数循环106次,可得到末端夹钳在操作空间中的106个工作点位(这些点在操作空间的分布集合表示了末端夹钳的工作空间),利用plot函数表示这106个点组成的工作空间云图,如图11所示。

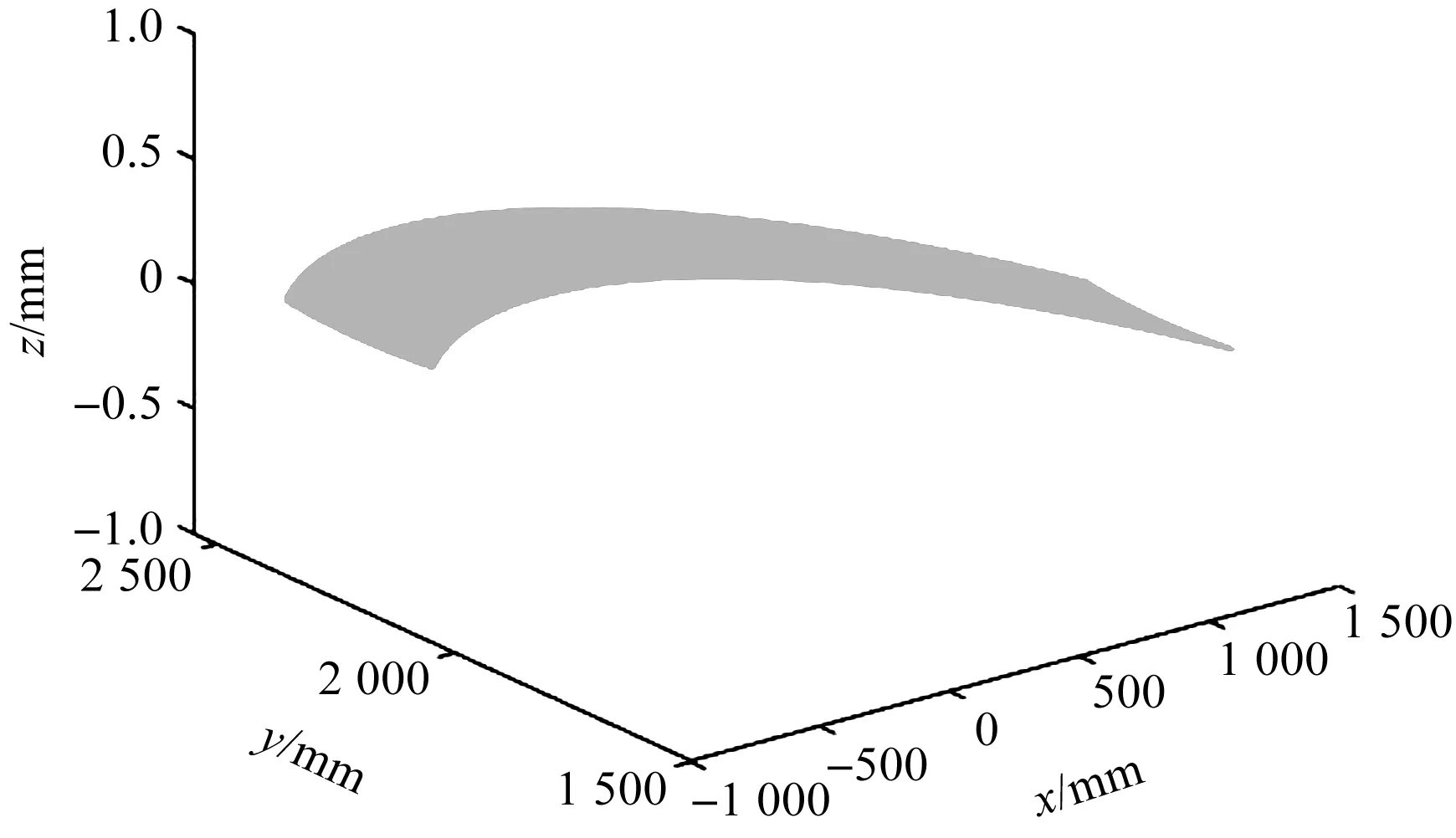
图11 工作空间三维图

工作空间云图在xoy平面上的投影如图12所示。

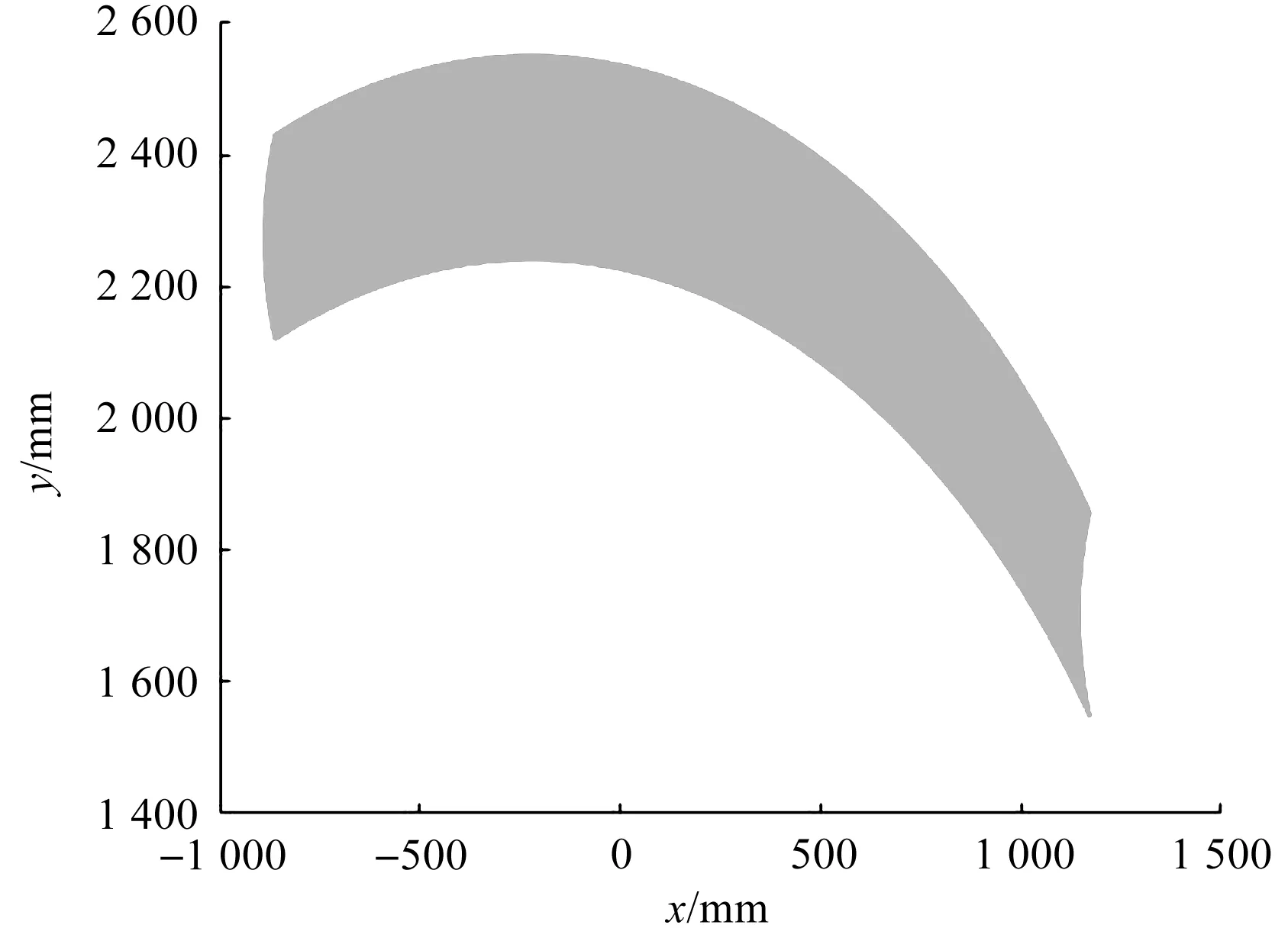
图12 xoy平面投影

图12中:由于机器人运动模型中的4个旋转关节轴线相互平行,且垂直于xoy平面,所以机器人仅在xoy平面内运动,而在xoz平面的工作空间云图投影为一条直线,因此,xoy平面内投影即为机器人的工作空间;

工作空间云图在xoy平面内的投影呈带状,末端夹钳水平方向的移动范围是-889 mm～1 172 mm,竖直方向移动范围是1 548 mm～2 551 mm,构造出了较大的工作空间,符合上料机器人转运轴类零件工作的要求。

4 机器人动力学分析

4.1 动力学仿真模型的建立

对机器人进行动力学分析时,为防止出现冗余约束的问题,笔者将图8中机器人三维模型进行简化,然后再将其导入ADAMS中,并依据图1对所导入模型进行标注。

所得到的上料机器人动力学模型如图13所示。

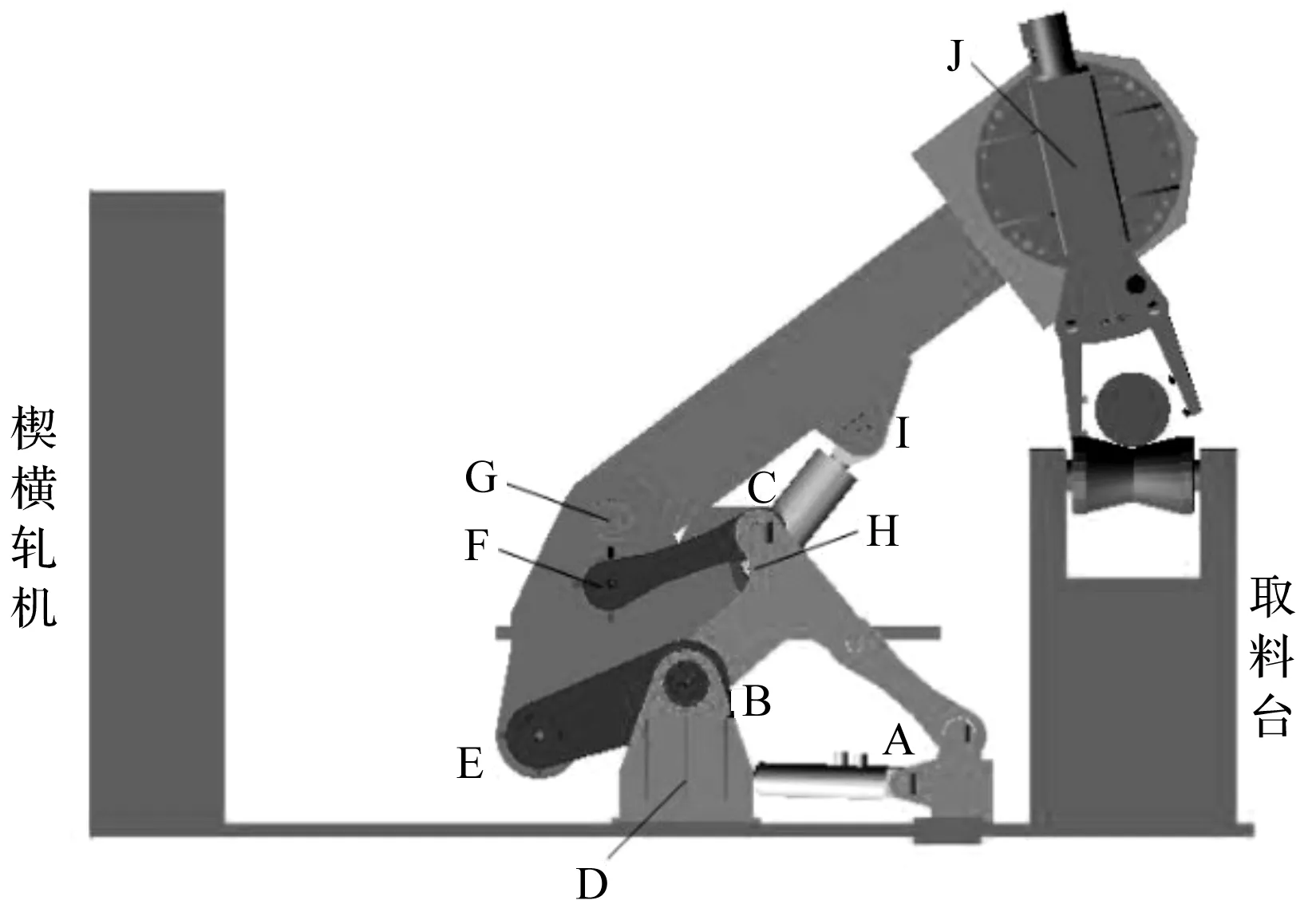
图13 上料机器人动力学模型

在图13中,机器人布置在楔横轧机与取料台之间,呈待夹取状态。当轴类零件经托辊传送至夹钳所能触及的位置时,夹钳夹取。夹取完成后,升降组件将摆臂底座抬升至高位,摆动油缸活塞杆伸长到中位,使大臂连杆摆动一定角度,翻钳部分翻转使得夹钳平行于地面,此时机器人整体呈摆动预备状态;

然后,摆动油缸活塞杆伸长到最大长度,使大臂连杆摆动至左极限位,同时,翻钳部分继续翻转,使得夹钳反向平行于地面;

最后,摆臂底座降至低位,完成机器人上料的动作过程。

机器人的工作范围主要由各驱动部件行程所决定,其中翻钳部分旋转角度范围是0°～125°。

各驱动油缸行程参数如表2所示。

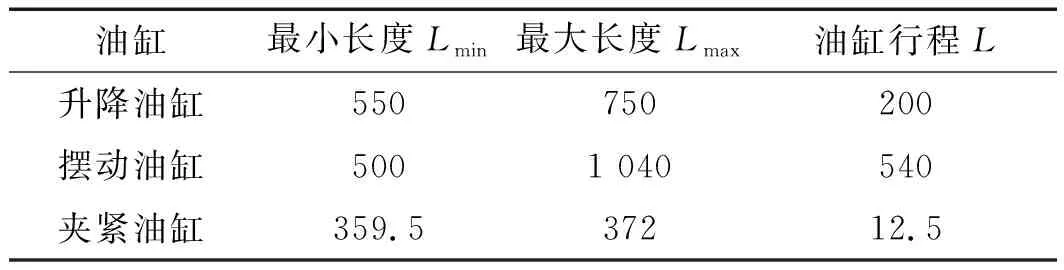
表2 各驱动油缸行程参数/mm

4.2 上料过程动力学仿真分析

笔者在ADAMS中,定义了机器人动力学模型的材料属性,适当添加了约束及运动副;由轴类零件尺寸参数及其材料属性,可得末端夹钳所受外载荷;利用STEP阶跃函数,分别对各驱动油缸的伸缩行程以及翻钳部分旋转角度进行控制;仿真时间设为10 s,仿真步数为200。

各驱动部件的阶跃函数如表3所示。

表3 各驱动部件阶跃函数

因为机器人承载较大,所以笔者只分析其带载转运工况。已知机器人的上料过程,以及完成其各项基本参数的设置,分析其各驱动部件与关键杆件上各铰接点的受力和力矩变化情况。

在上料过程中,各驱动油缸所受压力变化曲线如图14所示。

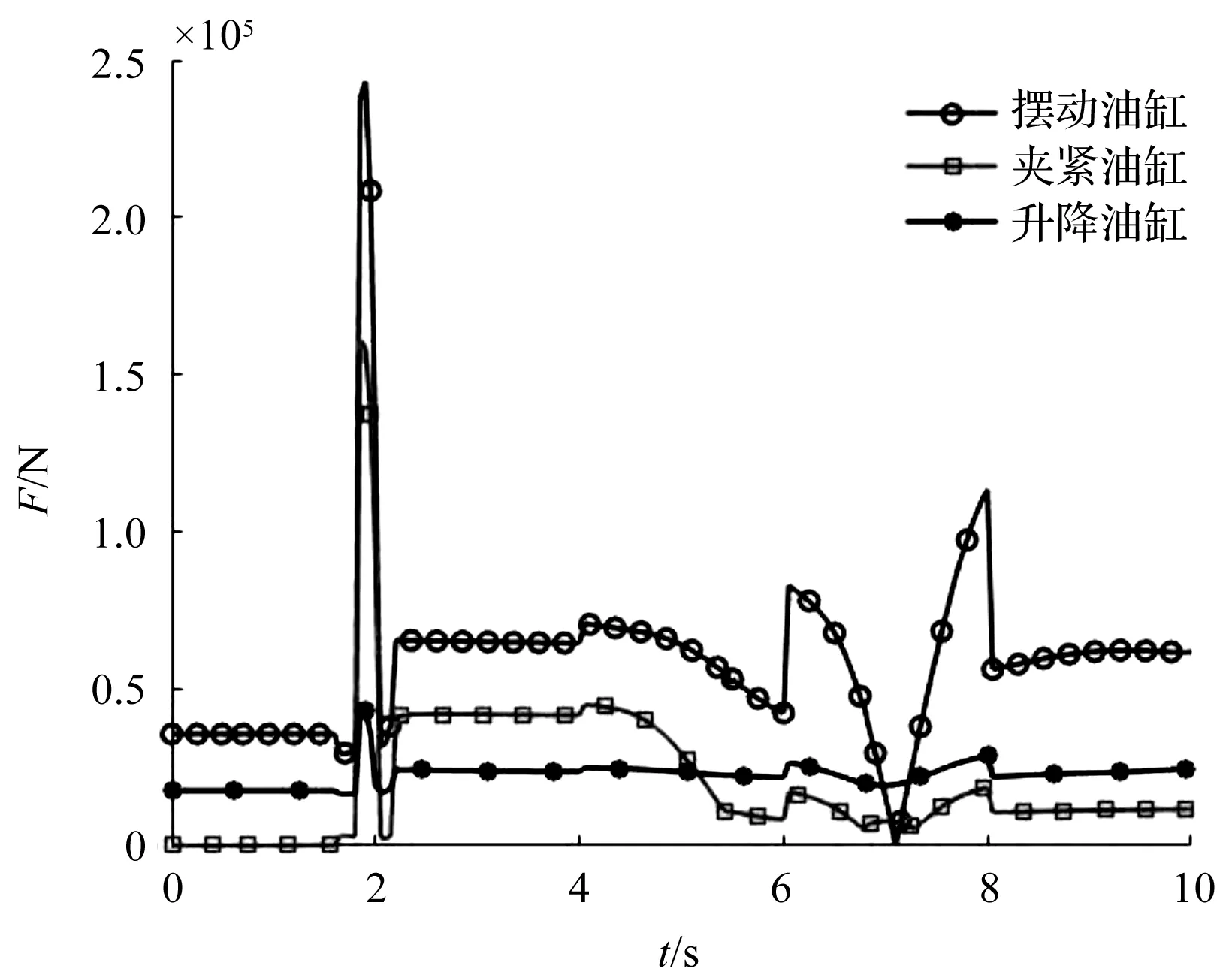
图14 各驱动油缸受力变化曲线图

在上料过程中,翻钳部分翻转力矩变化曲线如图15所示。

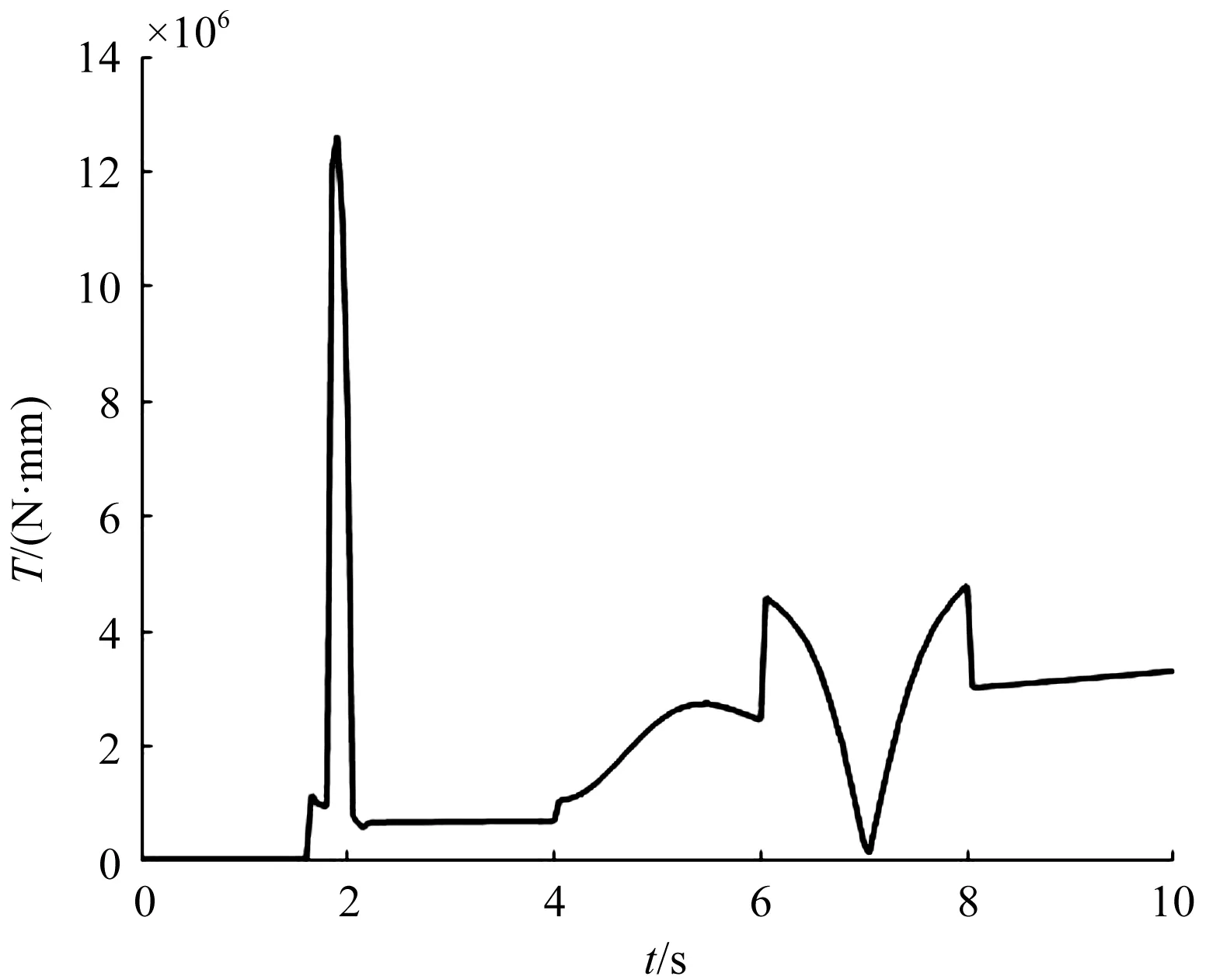
图15 翻钳部分力矩变化曲线图

由图14和图15可得:

在0～2 s时,机器人呈待夹取状态,各连杆仅受自重影响,升降油缸和摆动油缸的压力基本保持不变,夹紧油缸压力与翻钳部分翻转力矩均为0;

在2 s时,夹钳完成轴类零件的夹取,同时升降油缸驱动机器人上升;此时,由于轴类零件重力及升降油缸启动影响,在各油缸及翻钳部分上产生了力和力矩的突变;其中,摆动油缸的瞬间压力最大值可达240 kN左右;

在2 s～4 s内,各驱动部件驱动力和力矩平稳,升降油缸继续驱动机器人稳步上升;

在4 s时,摆动油缸与翻钳部分开始动作,分别驱动大臂连杆与夹钳绕各自旋转中心逆时针转动,各驱动力和力矩在启动时产生了微小的波动;

在4 s～6 s内,随着翻钳部分的逆时针转动,轴类零件质心与翻钳部分回转中心的水平距离逐渐增加,因此翻转力矩逐渐增加;而大臂连杆绕其回转中心的转动则使其质心与回转中心的水平距离愈来愈小,从而使摆动油缸驱动力逐渐减小;

在6 s时,机器人呈摆动预备状态,机身保持最高位状态不变,大臂连杆与夹钳继续绕各自旋转中心逆时针转动;

在7.1 s左右,大臂连杆垂直于地面,夹紧油缸轴线与大臂连杆共线,此时摆动油缸驱动力与翻钳部分翻转力矩近似回落到0,转过此位后会迅速回升,并在8 s左右分别达到100 kN、4.7 MN·mm,此时大臂连杆处于左极限位,夹钳反向平行于地面;

在8 s～10 s,升降油缸收缩,机器人降至最低位完成放料。

由图14曲线可知:摆动油缸与夹紧油缸受力均在机器人夹紧轴料抬升的瞬间发生明显振荡,但迅速恢复平稳;升降油缸受力曲线波动较小,验证了所设计升降组件能够保证机器人运行平稳。

大臂连杆上各铰接点的受力变化曲线,如图16所示。

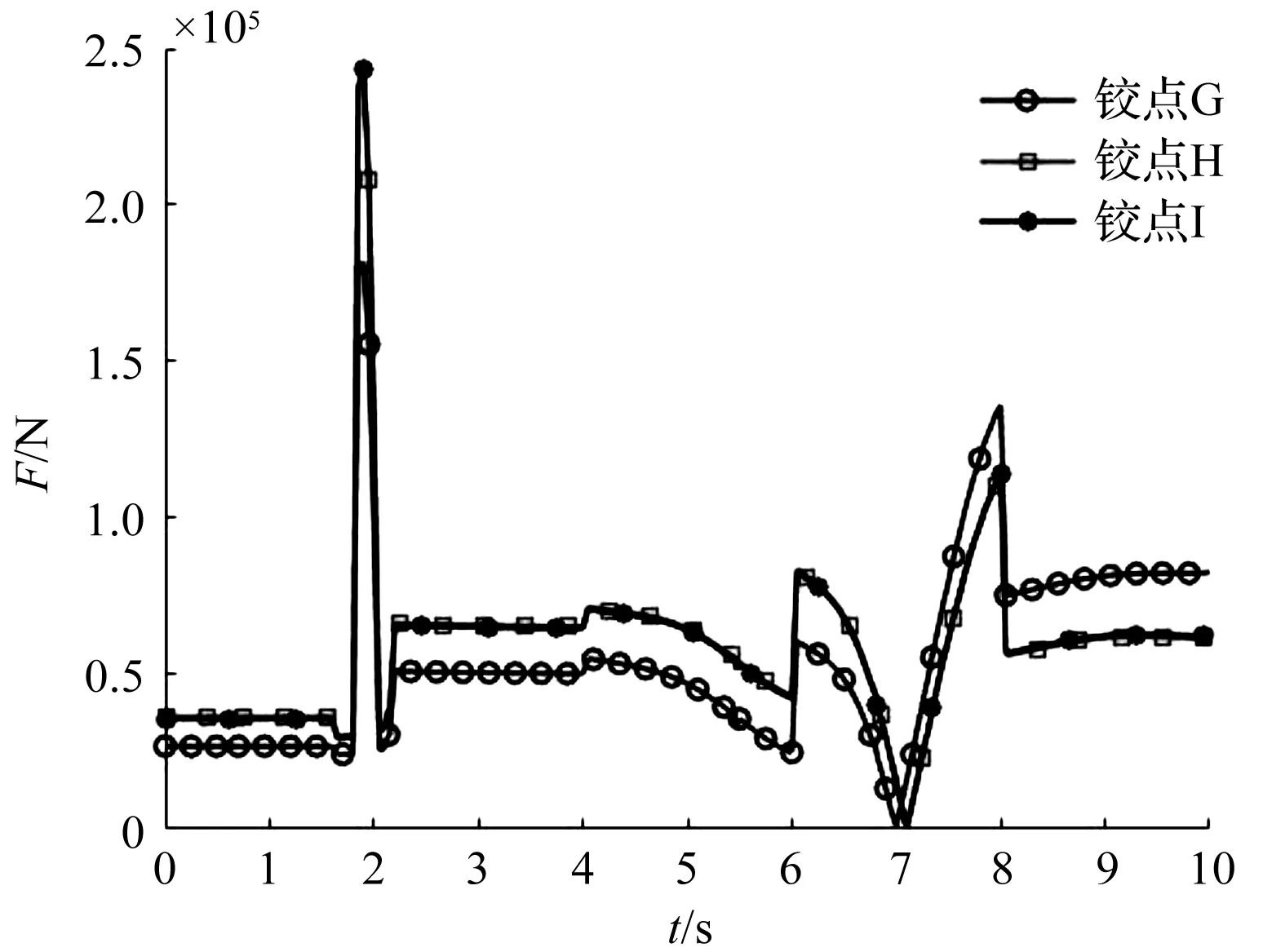
图16 大臂连杆各铰接点受力变化曲线图

由图16可知:各点受力变化趋势与摆动油缸压力变化相似,其中,铰接点H和铰接点I的受力变化曲线几乎重合。在0～2 s的空载期内,各受力曲线平稳;在6 s～8 s内,大臂连杆与翻钳部分同时完成了绕各自回转中心的旋转,形成了近似左右对称的受力变化曲线。

铰接点G是大臂连杆的回转中心,其受力峰值可达180 kN左右,因此,笔者在该处有针对性地使用了大直径连接销,并增加了连接板的厚度,验证了所设计大臂连杆结构的合理性。

大臂连杆上摆杆两端铰接点受力变化曲线,如图17所示。

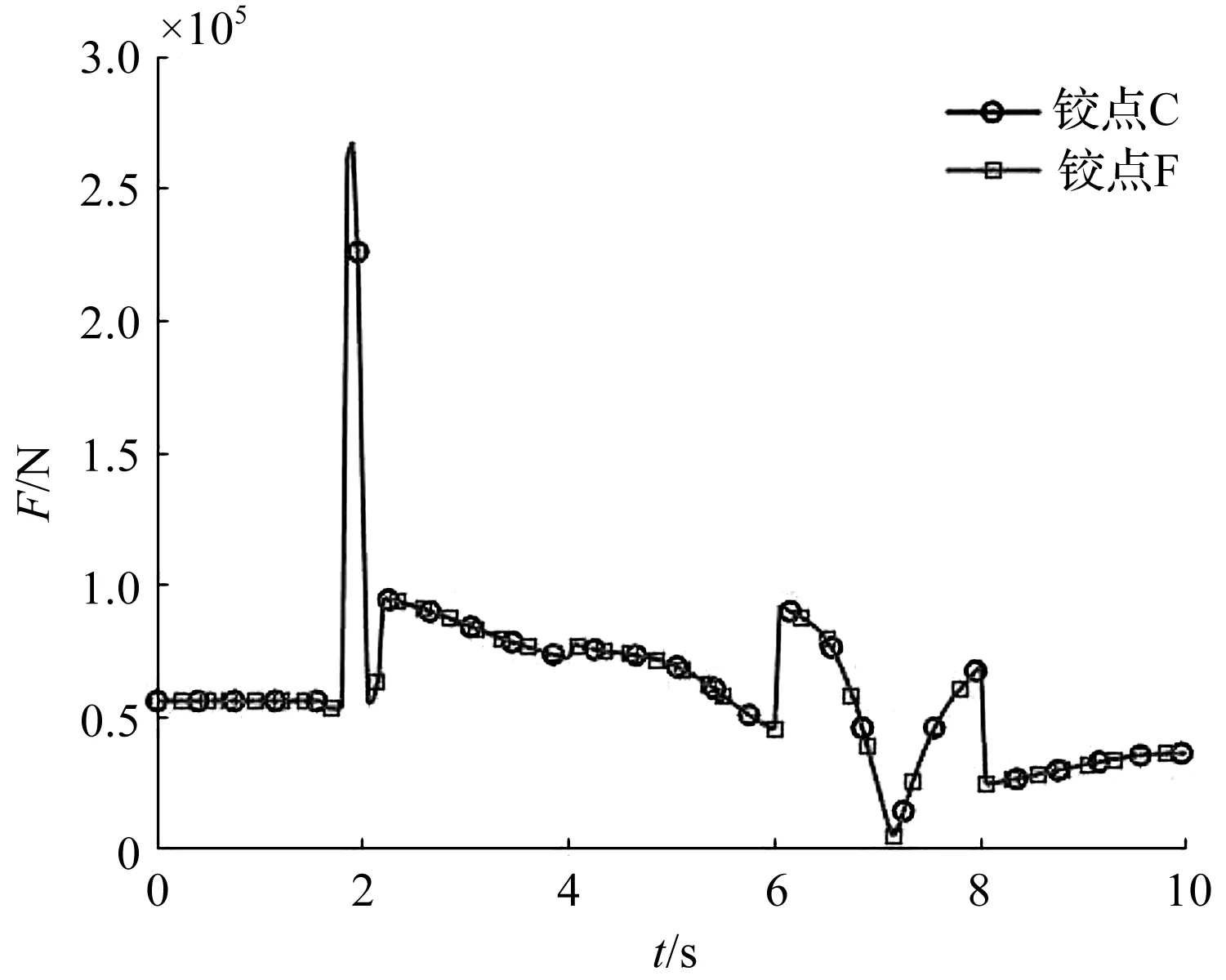
图17 摆杆各铰接点受力变化曲线图

在图17中,摆杆两端铰接点受力变化曲线几乎重合。

由图17与图16相比可知:相较于大臂连杆各铰接点,两铰接点的受力更大,因此,笔者在前述结构设计时,针对性地增加了摆杆两端铰接处圆形钢板的直径,提高了摆杆的连接强度。

该结果验证了摆杆结构设计的合理性。

5 结束语

为了解决超大型轴类零件楔横轧制生产中自动化程度低的问题,笔者设计了一种新型楔横轧上料机器人。

笔者依据机构运动原理简图,完成了机器人三维虚拟样机设计,并由标准型D-H参数法推导了机器人正逆运动学结果,建立了机器人的运动仿真模型,求解出了机器人的工作空间;利用ADAMS对机器人带载转运过程做了动力学仿真分析。

研究结论如下:

(1)机器人分别利用六连杆机构和四连杆机构实现了机身的升降运动与大臂连杆摆动,具有工作空间大、稳定性高等显著特点;利用回转关节和拉紧机构设计的可翻转自动夹钳,保证了机器人抓取的灵活性;

(2)机器人末端夹钳的水平移动范围为-889 mm～1 172 mm,纵向移动范围为1 548 mm～2 551 mm,验证了机器人工作空间大这一运动特性;

(3)动力学仿真分析得到机器人各驱动部件受力和力矩变化曲线图,及关键杆件上各铰接点受力变化曲线图。通过分析曲线变化规律与原因,验证了机器人结构设计的合理性与工作稳定性。研究成果为重载上料机器人的设计提供了模型参考。

在后续的工作中,笔者将从上料机器人所处高温轧制的实际工作环境出发,在温度载荷下,完成对机器人各关键部件的应力应变分析。