基于动态Nelson-Siegel模型的国债收益率曲线预测

张茂军，汤孝海，赵扬

（苏州科技大学商学院，江苏 苏州 215009）

引言

国债是中国债券市场的一个重要组成部分。收益率曲线是国债的重要属性之一，在宏观经济和金融市场中发挥着非常重要的功能和作用。在宏观经济方面，国债收益率曲线具有连接货币市场和宏观经济的功能，尤其是收益率曲线形状变化是宏观经济运行的“风向标”。在金融市场方面，国债收益率曲线是资产定价和投资的基础。

目前，关于国债收益率曲线的研究主要集中在对收益率曲线的拟合和预测两方面。大量文献研究了国债收益率曲线拟合模型，其中Nelson-Siegel模型不仅比较精确地拟合了国债收益率历史数据，而且可以分离出国债收益率的长期、中期和短期因子，是非常重要的模型之一。本文借助动态Nelson-Siegel模型拟合中国国债收益率曲线，同时利用AR模型和GARCH模型预测国债收益率曲线的水平因素、斜率因素和曲率因素，以期探究预测国债到期收益率的有效方法。

一、文献评述

国债收益率曲线的拟合模型主要分为动态仿射模型和参数模型。动态仿射模型又分为单因子仿射模型和多因子仿射模型。在单因子仿射模型中，通过设定收益率曲线受单一因素“短期利率”驱动，并在市场债券无套利条件下，推导出收益率曲线理论模型[1-3]。在多因素仿射模型中，在收益率曲线受若干潜在因素驱动的基础上，按照折现后债券理论价格同债券实际价格相等的原则，推出内含的收益率曲线[4-5]。但是，单因子和多因子仿射模型均是基于“某一时刻”的债券市场价格信息，样本外预测能力较弱。大部分动态模型侧重研究样本内数据拟合，甚少涉及样本外推检验和模型预测能力，也很少用于实际的收益率曲线预测。

在参数模型中，主要借助于多项式和样条方法拟合国债收益率曲线。McCulloch[6]提出了用分段多项式拟合收益率曲线的设想，并用三次样条法对美国国债税后收益率曲线进行估计[7]。Nelson和Siegel提出了拟合即期远期收益率的三参数模型[8]，这3个参数分别表示收益率的“水平”“斜率”和“曲率”状态因子，抓住了收益率曲线的特征，被广泛应用。近年来，Diebold和Li[9]在逐期估计Nelson-Siegel模型参数的基础上，提出动态Nelson-Siegel模型，对样本内参数建立时间序列模型，并预测样本外参数，即对收益率曲线进行预测。该方法不仅简洁，且具有显著的预测精度优势。Vicente和Tabak[10]利用动态Nelson-Siegel模型预测巴西债券市场收益率曲线，实证结果表明其对长期的预测效果优于其他模型。Yu和Zivot利用Nelson-Siegel三因素模型预测公司债券[11]，实证结果发现样本外预测时，AR（1）模型的表现优于其他模型。

国内学者对国债收益率曲线的研究也取得一些进展,如郑振龙和林海[12]、姚长辉等[13]、谢赤和吴雄伟[14]等的研究，但没有考虑国债收益率曲线预测问题。唐革榕和朱峰[15]、徐小华[16]的研究发现，国债收益率曲线90%以上的风险变动可以由水平、斜率和曲率3个因素解释。何晓群和王彦飞[17]分析了中国利率期限结构与宏观经济运行的关系。沈根祥和陈映洲[18]提出了双斜率因子动态Nelson-Siegel利率期限结构模型。魏立佳和蔡远飞[19]提出了利率期限结构的区制转移动态Nelson-Siegel模型。孔继红和岳伟[20]探讨了动态Nelson-Siegel模型的无套利约束相容。沈根祥和张靖泽[21]提出了条件异方差动态Nelson-Siegel利率期限结构模型。现有研究并没有把国债收益率曲线的整体作为研究对象，限制了国债收益率曲线的实际应用空间。

二、动态的Nelson-Siegel模型

在对收益率曲线进行拟合之前，首先考虑收益率计算问题。Pt(τ)表示在t时刻剩余期限为τ的零息债券价格，yt(τ)表示在t时刻剩余期限为τ的到期收益率，如公式（1）。

相应地，零息债券的即期远期收益率曲线如公式（2）。

因此，即期远期收益率曲线和收益率曲线之间的关系如公式（3）。

这就意味着，如果已知即期远期收益曲线ft(τ)，那么用式（3）可以计算零息债券的收益率。

实际中，不能直接得到收益率曲线、贴现曲线和即期远期收益率曲线，需要用债券价格估计。Nelson和Siegel（1987）提出了拟合即期远期收益率，如公式（4）。

由式（3）得到收益率曲线如公式（5）。

式（5）中，β1表示收益率的长期部分，随着时间t的逐渐增大，收益率将趋近于β1；β2表示收益率的短期部分，当它为正数时，收益率随着期限的增大而上升，反之相反；β3表示收益率的中期部分，决定了表示收益率的极值点和曲度；λ表示指数递减率，也是权衡短期和长期的拟合曲度。

中国诗歌中传达“意境”的思想源远流长，（陶渊明《饮酒》）“采菊东篱下，悠然见南山”中东篱是实实在在的事物，“东篱”后来常被诗人作诗用到。（李清照《醉花阴》）“东篱把酒黄昏后，有暗香盈袖”这句诗中的“东篱”便不是实指在东篱喝酒作乐，而是指一种意境。诗中的意象也是不胜枚举，例如关乎离别的意象是“杨柳”（杨柳东风树，青青夹御河）；关乎思念家乡的意象是“明月”（举头望明月，低头思故乡）；关乎思友的意象是“白云”（水底分明天上云，可怜形影似吾身）。译者要深入诗中意境观其意象，感受诗人此时此景的特殊情感，才能收受其意象的感染力。

在实际收益率曲线中，式（5）中的4个参数随时间变化。Diebold和Li（2006）提出了动态Nelson-Siegel三因子模型，收益率曲线表示如公式（6）。

其中β1t、β2t、β3t和λt都是时间函数。参数β1t的载荷因子为1，说明参数β1t体现了对收益率水平的长期影响因素；参数β2t的载荷为该载荷因子随利率期限的增加从1开始衰减至0，说明β2t是影响收益率的短期因素；参数β3t的载荷因子为该载荷因子随着利率期限的增加从0逐渐增大，并且经过某个拐点之后逐渐递减，直至衰减至0，这一特征说明了参数β3t是影响收益率的中期因素。

载荷因子解析式说明了收益率曲线的参数序列对收益率影响模式可分为长期、短期和中期。当利率的剩余期限趋于无穷时，yt()∞=β1t，说明参数β1t代表了长期收益率。短期因素β2t与收益率的斜率有关，参数β3t近似代表了衡量收益率曲线弯曲程度的中期收益率和曲率。

三、收益率曲线实证分析

本文采用2003—2021年的中国国债收益率数据。选取剩余期限为3、6、9、12、15、18、21、24、30、36、48、60、72、84、96、108和120个月的收益率数据，其中每个月为30.44天，数据来源于Wind咨询数据库。

本文参考Diebold和Li[9]的研究方法，为了分析收益率的水平、斜率、曲率3个因素的统计特征，以剩余期限是120个月的收益率为水平，以yt(120)-yt(3)=-0.78β2t+0.06β3t计 算 斜 率，以2yt(24)-yt(3)-yt(120)=0.00053β2t+0.37β3t计 算 曲率，并且分析收益率的相关统计特征，如表1所示。

分析表1可知，随着剩余期限增长，收益率均值也在以不同程度增长，说明收益率曲线有向上倾斜的趋势且长期比短期波动较小。进一步，比较3个因素延迟1个月、12个月、30个月的相关系数，分别用表示，可以发现：水平因素有高度的持久性，但其波动性却与其收益率均值相关性较弱；斜率因素持久性较弱，但波动性与其收益率均值相关性较强；曲率因素的持久性最弱，但其波动性与其收益率均值高度相关。

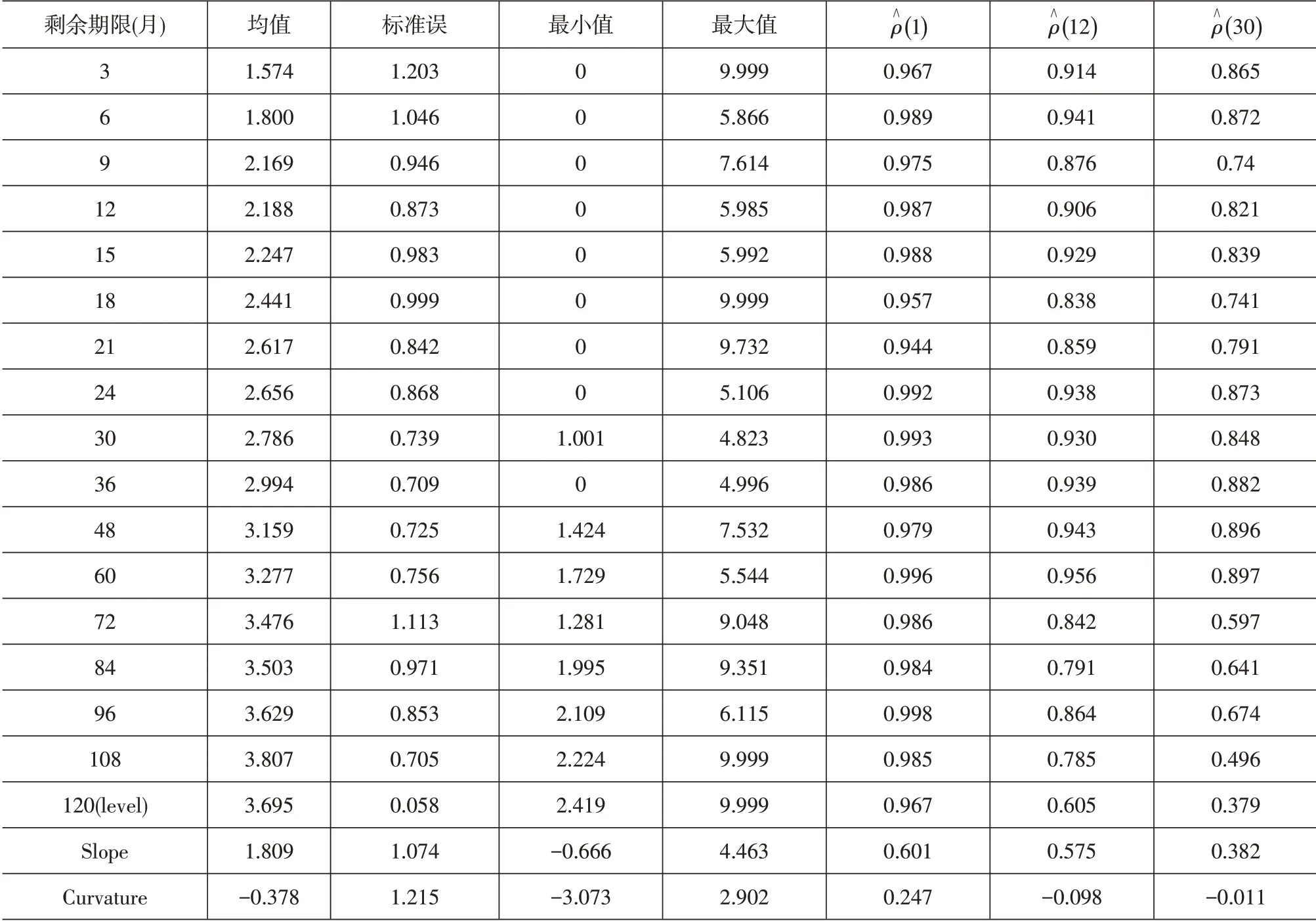
表1 收益率曲线统计性质描述

为了分析收益率的分布区间，图1给出了收益率中间值及其四分位数的分布情况，图中黑色曲线是收益率的75%分位数与剩余期限之间关系图，红色曲线为收益率中位数与剩余期限的关系图，绿色曲线为收益率的25%分位数与剩余期限的关系图。说明了收益率的分布在很长范围内是对称的，而且长期利率的波动比短期利率的波动小。

图1 收益率中位数、75%和25%分位数与剩余期限关系图

（二）拟合收益率曲线

借助于公式（6），用所选取的收益率估计参数β1t、β2t、β3t。图2展示了平均实际收益率曲线和拟合收益率曲线，其中红色为实际收益率曲线，绿色为由Nelson-Siegel模型拟合得到的收益率曲线。可以看出两条曲线之间非常相近。说明动态Nelson-Siegel模型可以很好地拟合收益率曲线。但在有些日期拟合效果并不显著，特别是收益率特别分散的时候。

图2 收益率和剩余期限关系图

表2描述了不同剩余期限到期收益率残差的统计性质。表2中，MAE表示平均预测绝对误差，RMSE表示均方根误差。最后3列是延迟1、12、30个月的残差自相关系数。从表中可以看出残差标准差随着剩余期限的增大有减小的趋势，即残差的波动随着剩余期限的增大而减小。由延迟1个月、12个月、30个月的相关系数得出相关性也随着剩余期限的增大而减小。残差样本的自相关系数意味着价差是持久的，但这种持久性将随着拟合收益率曲线的变化而消失。表3中，呈现了估计因素的统计性质。

表2 残差统计性质描述

由表3可知，3个因素延迟阶数的自相关系数说明第1个因素最持久。最后1列是增广Dickey-Fuller（ADF）单位根检验，说明存在单位根，具有非平稳性。

表3 估计因素统计性质描述

（三）预测收益率曲线理论模型

1.线性AR（1）模型。

式中i=1、2、3、ei,t+h是残差项，βi,t分别对应着动态Nelson-Siegel模型的3个参数。βi,t+h表示是βi,t在时间为h的预测项。

2.非线性AR（1）模型。

式中i=1、2、3、ei,t+h是残差项，βi,t分别对应着动态Nelson-Siegel模型的3个参数。βi,t+h表示是βi,t在时间为h的预测项。

3.线性GARCH模型。

式中i=1、2、3、wi是常数项，ei,t+h是残差项，是期望方差，βi,t分别对应着动态Nelson-Siegel模型的3个参数。βi,t+h表示是βi,t在时间为h的预测项。表示期望方差在时间为h的预测项。

基于上述3种模型，得到动态Nelson-Siegel模型的3个参数预测值，如公式（11）。

（四）动态Nelson-Siegel模型样本外预测

对动态收益率曲线进行拟合的模型，不仅要在样本内拟合效果明显，样本外预测结果也要显著。动态Nelson-Siegel模型中的3个参数决定了到期收益率大小，对收益率曲线的预测相当于预测动态Nelson-Siegel模型中3个参数的估计值表4中给出了预测1、6和12个月的误差分析。

表4展示了收益率曲线预测的3种模型所预测的收益率在前1个月、前6个月和前12个月的标准误。结果表明：线性AR（1）模型和非线性AR（1）模型在预测时的标准误随着预测时间的增大而减小，说明对远期利率的预测比短期利率的预测要精确。线性AR（1）模型预测的标准误同样说明，随着剩余期限的延长标准误增大，收益率曲线预测的误差增大。在比较线性AR（1）模型、非线性AR（1）模型和GARCH模型预测效果时，AR（1）模型对收益率曲线的短期和长期预测都比非线性AR（1）模型和GARCH模型要好。

表4 预测误差

结论

本文将动态Nelson-Siegel曲线的3个参数作为收益率的水平、斜率和曲率因素进行拟合预测，得到了有效结果。3个因素动态变化特征从整体上反映了收益率曲线变化特征。在对收益率曲线进行预测时采用线性AR（1）模型、非线性AR（1）模型和GARCH模型，通过比较3种模型预测的标准误，发现AR（1）模型对收益率曲线的短期和长期预测都比非线性AR（1）模型和GARCH模型精确，且能够很好地刻画收益率曲线整体动态变化规律。研究结论说明，通过合理的设计，收益率曲线变化在某种程度上是可预测的。该结论对债券投资、套期保值和利率免疫有着重要的实践意义。