团雾成因的GWR和MGWR建模及其差异性分析
杨作林,冯海霞,商强,郑文剑,周昕,闫祥
(1.山东理工大学 交通与车辆工程学院, 山东 淄博 255049;2.山东交通学院 交通与物流工程学院, 山东 济南250399)
团雾与雾的本质相同,又名“坨坨雾”,是受局部地区微气候环境的影响,在大雾中数十米到上百米的局部范围内,出现的比普通的雾更“浓”的雾。通常,团雾外视线良好,团雾内能见度极低。团雾具有区域性强、预测预报难的特点。若高速公路上出现团雾现象,则极容易因能见度低而酿成重大交通事故。
团雾带来的危害及后果十分严重,引起了国内外各界人士的注意,研究人员也对团雾现象的规律进行了相关分析及研究。Tang等[1]根据团雾的特点、影响范围、到达强度和持续时间,结合公路、交通和地形因素,建立了雾天公路网交通状况预警指标体系。丁秋冀等[2]统计并研究了2006—2009年团雾发生的不同路段及其温度、湿度、地形环境等地理条件、自然条件和气候条件,以探索高速公路团雾发生的规律。杨西海等[3]分析了团雾的危害和形成条件等,提出了应对德上高速团雾发生的防治和预警措施。梁莉等[4]针对发生在安徽阜阳滁新高速的团雾交通事故,根据多项天气地势数据,探讨引起团雾发生的主要因素。王健等[5]通过总结团雾的特征与发生规律,以及团雾在高速公路引起交通事故的特点,分析团雾对高速公路交通安全的影响。此外,国内外有关专家也对MGWR进行了相关研究,MGWR延续了GWR的功能,并且相较于GWR,在变量的空间尺度上有了进一步拓展。Fotheringham等[6]运用向后演算法进行MGWR中的模式校正和宽带向量选择,将GWR和MGWR架构运用至两组具有已知属性的虚拟数据集并比较了两者的表现,发现MGWR不仅在复制具有不同层级空间变异性的参数表面上表现较佳,更提供了有关不同过程所进行的尺度的宝贵信息。郑娟[7]在考虑不同变量空间尺度的基础上研究了MGWR,通过随机模拟实验对MGWR模型的拟合效果进行的分析结果显示,MGWR模型的系数曲面还原能力和拟合效果都优于GWR模型。Fotheringham等[8]利用MGWR评估了中国空气污染的影响。Mansour等[9]对COVID-19发病率的社会人口学决定因素开展了研究。本文以2018年山东省内的团雾多发点数据为基础展开研究,尝试运用GWR和MGWR模型对团雾形成潜在的几个诱因进行相关性和作用尺度的分析。
1 研究区概况、数据来源和变量选择
1.1 研究区概况
山东省是中国华东地区的一个沿海省份,简称“鲁”,位于北纬34°22.9′~38°24.01′、东经114°47.5′~122°42.3′之间,自北向南分别毗邻河北省、河南省、安徽省、江苏省。山东省属暖温带季风气候,中部地区山地较多,其中以泰山为海拔最高点,海拔为1 532 m;西南、西北地区地势低洼平坦;东部为山东半岛,地势以山地和丘陵为主。山东省地貌特征丰富,包含山地、丘陵、台地、盆地、平原、湖泊等多种类型地形地貌。
本文旨在研究山东省内各团雾多发点的团雾发生次数与团雾多发点周围4 km区域内的高程差、河流分布与高速公路分布之间的关系。研究区域为山东省陆地。
1.2 数据来源
本研究所使用的原始数据包含山东省数字高程模型(digital elevation model,DEM)、山东省水文图和山东省团雾高发点坐标及其团雾发生次数等。山东省DEM由空间地理数据云官网(http://www.gscloud.cn/#page1/2)提供原始数据,并经由ArcMap执行按掩膜提取功能获得;山东省河流分布矢量图和高速公路分布矢量图由空间地理数据云(http://www.gscloud.cn/#page1/2)获得,团雾数据由公安部交通管理局提供。
1.3 变量选择
本研究认为团雾的发生是当地水文、海拔、高速公路分布等多个地理条件和自然条件综合作用引起的。选定多发点周围区域内高程差(下文简称“高程差”)、多发点周围区域内河流长度(下文简称“河流长度”)、多发点周围区域内高速公路长度(下文简称“高速公路长度”)为解释变量,选定“团雾年发生次数”为因变量。
2 研究方法
2.1 地理加权回归
地理加权回归(GWR)是一种空间分析模型,已经被广泛应用于经济、自然资源管理、医学、地理信息系统等多个研究领域中,通过建立空间范围内每个点处的局部回归方程来探索研究对象在某一尺度下的空间变化及相关驱动因素,并可用于对未来结果的预测。
地理加权回归是对普通线性回归模型的扩展,将数据的空间位置嵌入到回归方程中,其数学表达式为
i=1,2,3…,n,
(1)
式中:Yi为因变量;β0(ui,vi)为截距;Xik为第k个解释变量在第i个采样点的值;(ui,vi)为采样点坐标;βk(ui,vi)为采样点(ui,vi)上的第k个回归参数;εi为随机误差。
2.2 多尺度地理加权回归
在空间数据分析中,虽然GWR作为一种最普通最常用的方法,可以用来分析自变量与因变量之间的关系,但该模型未能描述空间位置的特殊性——空间非平稳性或空间异质性,因而不能全面有效地反映出空间数据的真实属性。近年来,Fotheringham等多名学者对多尺度地理加权回归模型进行了研究[6-9]。多尺度地理加权回归模型作为一种有效的探测空间数据分析法已经广泛应用于各个领域,它是对GWR的一个显著改进,因为它放松了“相同的空间尺度”假设,并允许优化解释变量的特定带宽,其表达式为
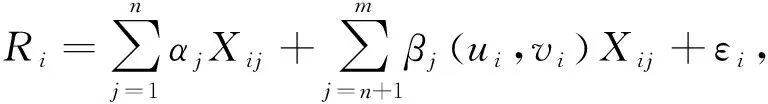
i,j=1,2,…,n,
(2)
式中:Ri为因变量值;Xij为解释变量的数值;(ui,vi)为第i个采样点的坐标;j为自变量个数;αj为全局变量的回归系数;βj为局域变量的回归系数;εi为随机误差。
3 原始数据展示与数据预处理
3.1 原始数据
3.1.1 团雾数据
团雾发生数据由公安部交通管理局提供,部分数据见表1。
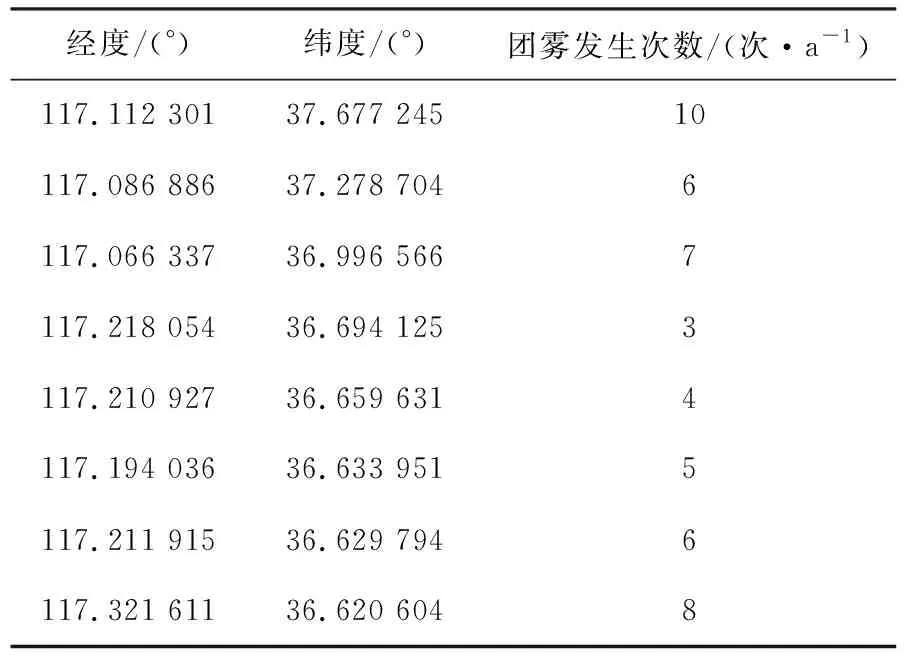
表1 团雾数据举例展示(列举部分)Tab.1 Samples of mass fog data (partial)
3.1.2 矢量数据
本研究所采用的解释变量包含团雾发生点周围4 km区域内的河流长度和高速公路长度,能够直接获得且与此相关的数据为山东省河流分布矢量图和山东省高速公路分布矢量图,如图1所示。
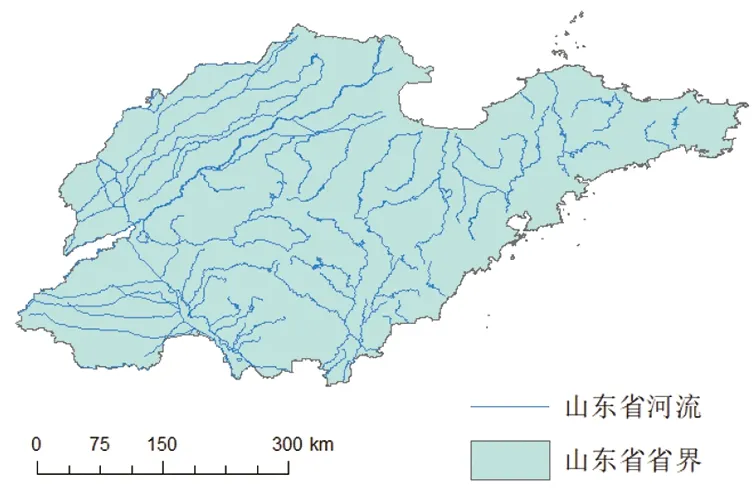
(a)河流
3.1.3 栅格数据
本研究的解释变量含有团雾多发点周围4 km区域内的高程差,能够直接获得的与此相关的数据为山东省及周围部分地区的DEM。经过“按掩膜提取”操作得到的山东省DEM如图2所示。
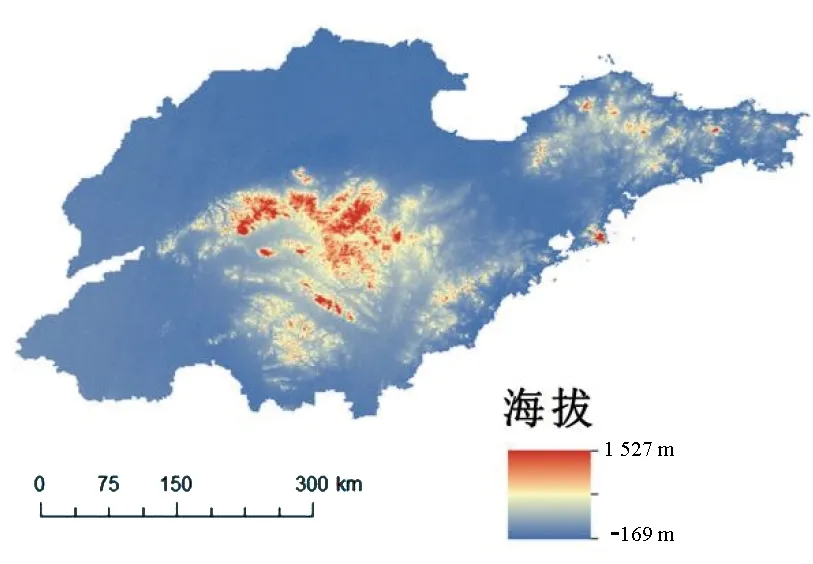
图2 栅格数据Fig.2 Raster data
3.2 数据预处理
数据预处理即将能够直接获取的原始数据加工为所需数据的过程。本文已说明能够直接获取的原始数据,现将之分别加工为:团雾多发点矢量点层数据、团雾多发点周围4 km区域内河流长度、高速公路长度和高程差。该过程可以在由Esri公司研发的软件ArcMap中实现。数据预处理的流程如图3所示。
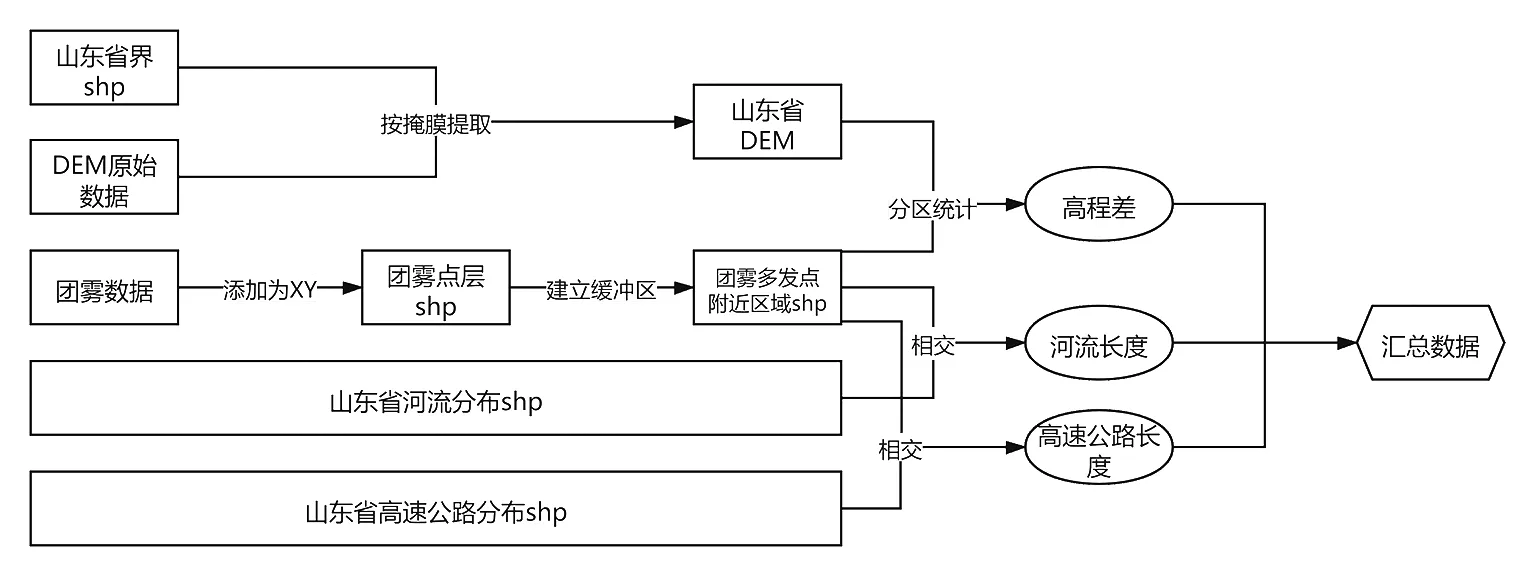
图3 数据预处理流程Fig.3 Process of data pre-processing
3.3 数据预处理结果与分析
经过数据预处理,得到包含解释变量和因变量的汇总数据见表2(列举部分数据)。
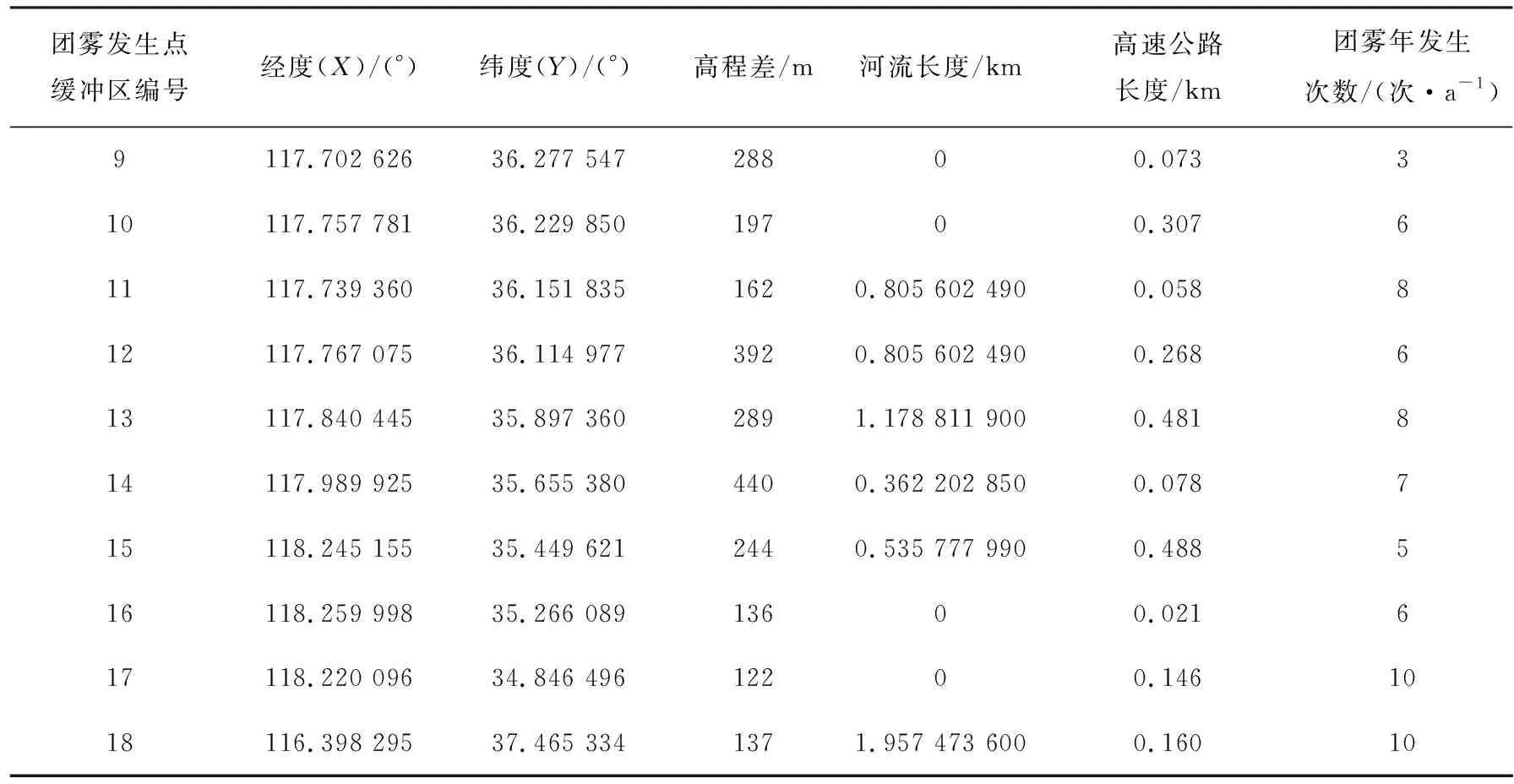
表2 汇总数据展示(列举部分)Tab.2 The data summary(partial)
现对上述数据进行可视化处理。将表2数据作为XY数据导入至ArcMap中导出点层数据,并对其进行符号系统分类,效果如图4所示。
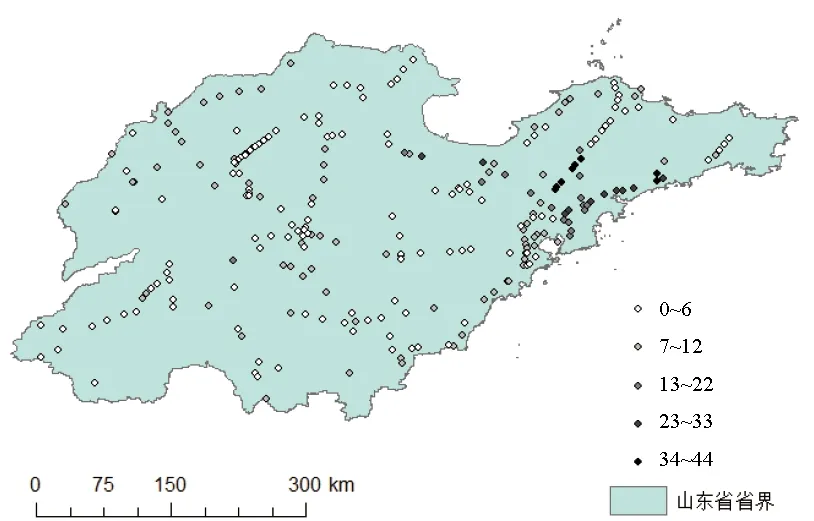
图4 团雾年发生次数分布Fig.4 The distribution of annual frequency of mass fog
由图4可以看出团雾年发生次数分布格局大致为:鲁东地区尤其是青岛市周围地区,团雾发生次数较多,2018年该区域发生团雾次数可达12至44次;鲁西地区及鲁中地区团雾发生次数较少,多数地区2018年发生团雾次数不超过10次。
4 结果及分析
4.1 GWR结果及分析
GWR的对象是经过数据预处理获得的一个包含坐标、自变量和因变量的数据表,如表2所示。GWR可以在由Esri公司研发的软件ArcMap中实现,其结果见表3。
表3中,R2为拟合优度,R2的值在0到1之间,越接近于1,说明自变量与因变量之间的相关性越强,即自变量对因变量的影响效果越强。若某自变量R2=1,则代表因变量只受到该自变量的影响;若R2=0,则代表该自变量对于因变量无任何影响。表3展示的是对所有变量的GWR分析,代表高程、河流长度和高速公路长度3个变量的综合作用效果,其R2为0.695 685 923。
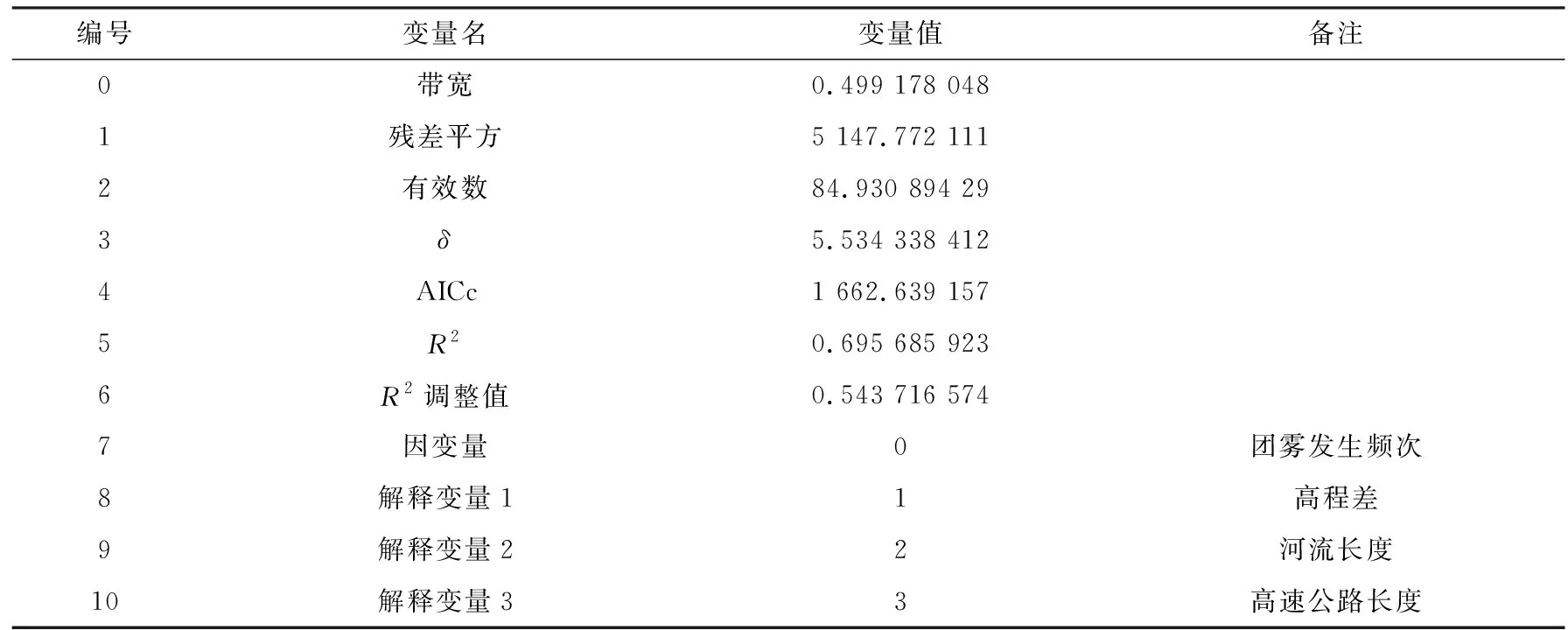
表3 GWR结果Tab.3 The result of GWR
下面分别对3个变量进行GWR分析,得到3个自变量各自的R2即可判断不同自变量对团雾发生影响作用的强弱。3个自变量的R2和带宽见表4。
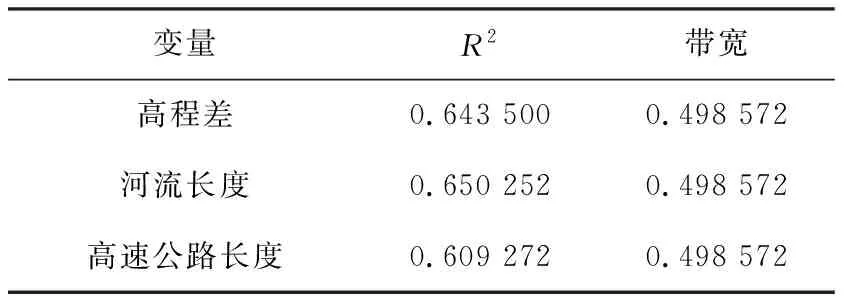
表4 变量R2和带宽Tab.4 The R2 of variables and bandwidths
由表4可知,河流长度的R2略大于其他两个自变量。这表明,河流长度相较于高程和高速公路长度,其与团雾发生的相关性略强。
变量的带宽代表变量的作用尺度。带宽越小,意味着变量的空间尺度越小,意味着变量的空间异质性越强,意味着自变量与因变量之间的关系随着地理位置的变化越剧烈。在上述结果中不难发现,3个自变量得到的是相同的带宽,均为0.498 572。这说明,GWR模型在回归过程中,默认所有的变量具有相同的空间尺度和带宽,忽略了不同变量之间空间异质性的差异。
4.2 MGWR结果及其可视化
MGWR的分析对象也是经过数据预处理得到的包含经纬度坐标、自变量和因变量的数据表,MGWR可以用软件MGWR 2.2来实现。
4.2.1 自变量回归系数分析
现将每一个变量的回归系数进行可视化操作,其方法与汇总数据的可视化相同,可视化操作的结果如图5所示。由图5可知各个变量估计系数的分布格局,进而得知其影响作用的强弱与正负。
常数项对于团雾的产生,在鲁西地区及鲁中地区皆呈现负向影响,在鲁东半岛地区尤其是青岛市周围的沿海地区呈现显著且强烈的正向影响,如图5(a)所示。
河流长度对于团雾的产生呈现显著的正向影响,在山东省全部地区,其自变量估计系数均为正值。高值出现在鲁东半岛地区,低值出现在鲁西地区及中部地区,如图5(b)所示。
高速公路长度对于团雾的产生同河流长度相似,在山东省全部地区均呈现正向影响,且高值出现在鲁东半岛地区,低值出现在鲁西地区和中部地区,如图5(c)所示。
高程差对于团雾的产生似乎与其他的变量截然相反——呈显著的负相关,意味着地势越平坦的地区越容易发生团雾。鲁东地区平原较多,团雾发生也相对较多,如图5(d)所示。
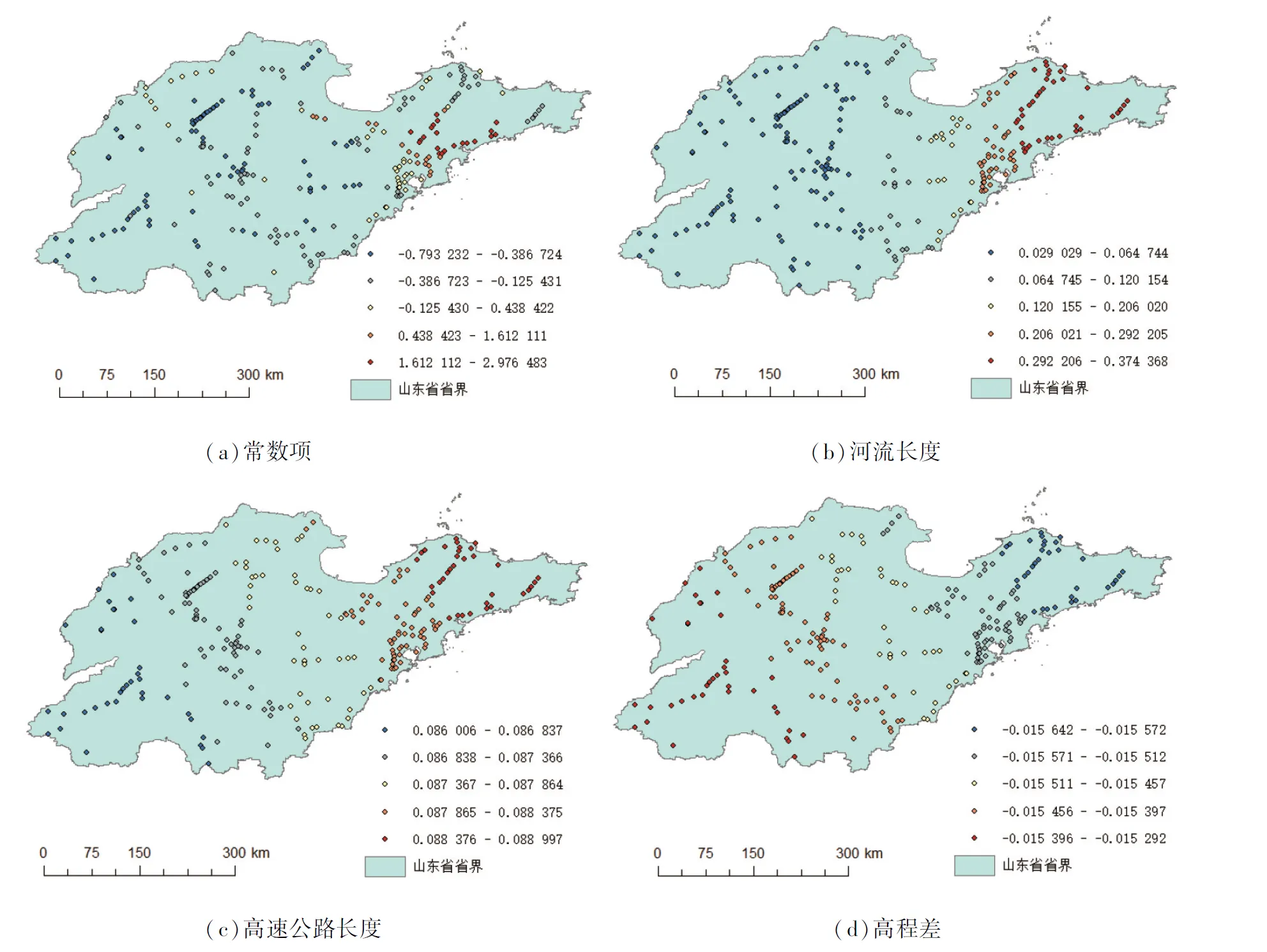
图5 自变量回归系数可视化结果
河流长度与高速公路长度对于团雾的发生均呈现正向相关,但是通过观察两个变量的变量估计参数不难发现,河流长度的变量估计参数略高于高速公路长度的变量估计参数,这意味着河流长度对于团雾发生的促进作用略微强于高速公路长度。这个结论,和前文比较两个变量的R2得到的结论相一致。
4.2.2 自变量空间尺度分析
GWR在回归中,默认所有的变量具有相同的空间尺度以及相同的带宽,忽略了变量之间空间异质性的差异。MGWR则允许各个变量带宽不同, 改进了经典地理加权回归GWR,进而得到了更为可信的估计结果,同时给出了不同变量的影响尺度。变量分别经由GWR和MGWR所得到的带宽见表5。
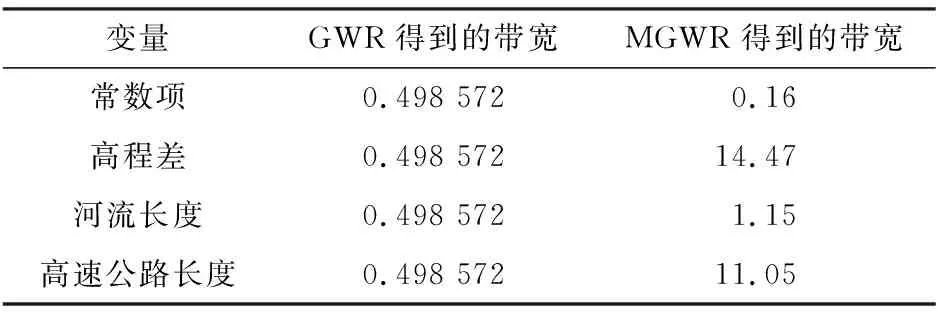
表5 GWR与MGWR所得到的变量带宽Tab.5 Bandwidth of variables from GWR and MGWR
表5显示,只有在MGWR的结果中才可以看出不同变量的作用尺度差异较大。其中,高程差带宽为14.47,高速公路长度带宽为11.05,明显大于常数项和河流长度的空间尺度, 空间异质性较弱。常数项代表在其他的自变量保持不变的情况下,地理位置对于因变量的影响,常数项的带宽为0.16,明显低于其他变量,空间异质性很强,代表团雾的发生对于地理位置很敏感。河流长度的空间尺度为1.15,尺度相对于高程小了很多,但高于常数项,表明河流长度和高速公路长度的影响也存在一定的空间异质性,但弱于常数项。
5 结束语
高速公路上的团雾是受到多种自然条件和地理条件的共同作用而形成的,如当地的地形地貌地势、水文、高速公路分布情况等。通过GWR分析得知,河流长度对团雾发生的促进作用略大于高速公路长度和高程的作用。MGWR分析也证实了这一结论。此外,MGWR的结果显示:高程的作用尺度为14.47,略高于高速公路长度的11.05,明显高于常数项的0.16和河流长度的1.15,具有变量中最大的空间尺度和最小的空间异质性。高程对于团雾的发生具有反作用,即在平原地形较多的鲁东地区,团雾发生较多;在山地丘陵较多的鲁西地区,团雾发生往往较少。团雾周围河流长度和高速公路长度对于团雾的发生有正向作用,即高速公路上越靠近河流的地点,团雾越容易发生。
根据以上结论,可以大致得到一个高速公路上预测团雾的行驶方案:即在山地丘陵地带,团雾发生较少,大多数情况下可以放心通行;在平原地带,靠近河流的地点应格外注意。
本研究依然有如下不足:选取的自变量种类较少,而团雾的潜在成因还有很多,如年平均气温、空气湿度等其他自然和地理条件;选取样本范围较小,仅为山东省,导致样本点数量较少,仅有250余个样本,缺乏一般性。今后可获取更多的数据和样本进行深入研究。

