叉车线控转向执行电机控制策略研究
曲浩,曲宝军,周海安,刘惟栋,韩宗旺,车科
(1.山东理工大学 机械工程学院,山东 淄博 255049;2.山东先河悦新机电股份有限公司,山东 淄博 255022)
随着科学技术的发展,人们对效率的追求也在逐渐提升,叉车也越来越多地参与到经济发展和社会建设中[1]。叉车是一种重要的物流运输设备,在码垛、拣选和搬运等诸多活动中得到广泛的应用[2]。线控转向系统作为一种新型的转向系统,其主要特征是将转向盘和转向轮之间的机械连接部分用电信号代替,因此可以自由设计转向时的传动比,使叉车的转向性能得到极大提高[3-4]。目前,虽然国内的各汽车生产厂商和科研中心在线控转向方面加大了科研力度,但研究成果和国外相比较仍存在较大差距[5],因此对叉车线控转向系统的研究非常重要[6]。永磁同步电机因功率密度高、调速范围大、响应速度快等优点,在对要求精度和可靠性较高的场合得到了广泛的应用[7]。本文采用永磁同步电机作为线控叉车转向执行电机,设计能够满足叉车转向特性的电机控制策略,并从仿真层面验证其有效性。
1 转向执行电机选型和控制策略设计
1.1 转向执行电机选型
转向执行电机的选型一般从响应和负载两个角度考虑。目前在线控转向系统中通常用直流电机作为转向执行电机,但是其存在效率低、发热高、寿命短等问题。永磁同步电机具有同尺寸直流电机达不到的较高电磁转矩,且具有效率高、响应快、更容易实现转矩精确控制等优点[8]。综上所述,本文的转向执行电机选用表贴式永磁同步电机。
1.2 转向电机控制策略的制定
永磁同步电机结构如图1所示,转子部分是永磁体,定子上安装有对称的绕组。

图1 永磁同步电机结构示意图Fig.1 Structure diagram of permanent magnet synchronous motor
三相电压方程如下:
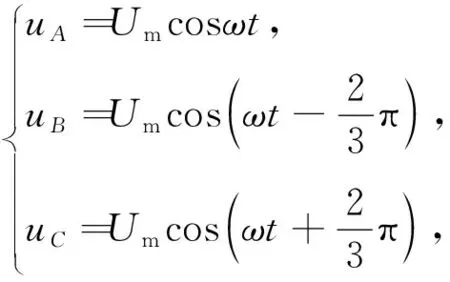
(1)
式中:uA、uB、uC为三相对称正弦相电压的瞬时值;Um为相电压的幅值;ω=2πf为相电压的角频率。
三相电压方程在自然坐标系下的表达式为

(2)
磁链方程为
ψ3s=L3si3s+ψf·F3s(θe),
(3)
式中:ψ3s为三相绕组磁链;L3s为三相绕组的电感;i3s、R3s、u3s分别为三相绕组的相电流、电阻和电压;ψf为永磁体磁链。
电磁转矩Te为
(4)
式中:pn为电机极对数。电机的机械运动方程为
(5)
式中:TL为负载转矩;B为阻尼系数;ωm为电机机械角速度;J为转动惯量。
因为转矩受转子位置和时间等参数影响,一般方法难以对其实现精确控制,通常采用的方法是通过Clark变换、Park变换、Park逆变换,将永磁同步电机的控制等效为对直流电机的控制。
在永磁同步电机的控制中,矢量控制的应用使得永磁同步电机在调速性能上与直流电机十分类似[9];因此,本文选择id=0的矢量控制策略,以期更加准确地控制永磁同步电机的电磁转矩,同时使永磁同步电机的速度、位置的控制更精准。
文献[3]采用了传统三闭环控制策略作为叉车转向执行电机控制策略,但其存在系统响应过慢的问题。因此,本文在矢量控制基础上设计了一种基于模糊控制的三闭环(电流环、速度环、位置环)控制策略,控制策略原理如图2所示。

图2 控制策略原理图Fig.2 Schematic diagram of control strategy
1.3 模糊PID反馈环节的设计
传统控制方法需要获得受控对象精确的数学模型,但是在实际的工程应用中很多受控对象的数学模型很难建立,导致了控制效果并不理想[10]。为了解决这个问题,现代控制策略里便有了把PI控制和模糊控制相结合的复合控制策略[11]。模糊控制是非线性的控制方法,不需建立受控对象的精确数学模型,而是通过模糊控制器实现的[12-13]。
在本文所设计的三闭环控制策略中,如果速度环采用传统控制方法(普通PI控制),则负载直接作用在电机上产生的扰动会使得系统响应速度变慢,而模糊控制技术能够在较短时间内实现系统的动态调节并能够快速响应。所以为了实现对永磁同步电机的高精度控制,本文在位置环与电流环采用传统控制策略的同时,在速度环采用PID模糊控制器。具体思路为:首先计算前轮位置与方向盘之间的误差,通过位置环PI调节输出由位置误差引起的参考速度;然后在速度环计算转子速度与参考速度之间的误差,通过模糊PID调节输出q轴的参考电流分量;之后通过计算dq坐标系的实际电流分量和输入的参考电流之间的误差,再经过电流环PI调节输出电压;最后,PWM信号通过SVPWM算法产生,从而驱动电机运转。
1.4 模糊PID控制器的设计
设e为误差,ec为误差变化率,u为输出[13]。首先,把e和ec模糊化处理,并将处理后的数据输入模糊控制器;然后,将两个输入通过模糊规则进行模糊推理,推理后的模糊值通过解模糊化后再乘以比例系数得到ΔKp、ΔKi、ΔKd;之后,将模糊处理后的值与原值通过加法运算得到一组新的PID值;最后,通过得到的新的PID值求出控制程度u。模糊控制原理如图3所示。
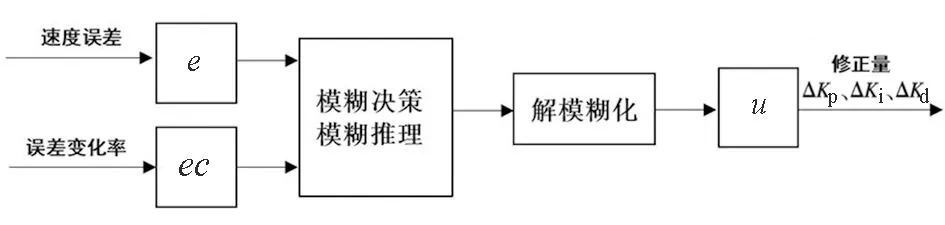
图3 模糊控制原理图Fig.3 Schematic diagram of fuzzy control
根据模糊规则,采用“负大”、“负小”、“零”、“正小”、“正大”的模糊语言集,设置模糊子集语言变量的7个元素对应模糊子集{NB NM NS ZO PS PM PB}。将输入量变换到模糊域值得到模糊域:输入值e和ec采用相同论域[-1.2,-0.8,-0.4,0,0.2,0.4,0.8,1.2]。
设置输出量ΔKp、ΔKi、ΔKd的模糊论域都为[-1,-0.8,-0.4,0,0.4,0.8,1]。隶属函数选择Gauss型函数,如图4所示。

图4 e、ec的隶属函数Fig.4 Membership function of e、ec
为了使系统的响应速度和控制精度达到要求,在对模糊规则进行设计时,既要考虑整个系统的稳定性,又要考虑超调不能太大,所设计的模糊规则见表1—表3。得到的PID模糊控制规则曲面图如图5所示。

表1 ΔKp的模糊控制规则Tab.1 Fuzzy rule control of ΔKp
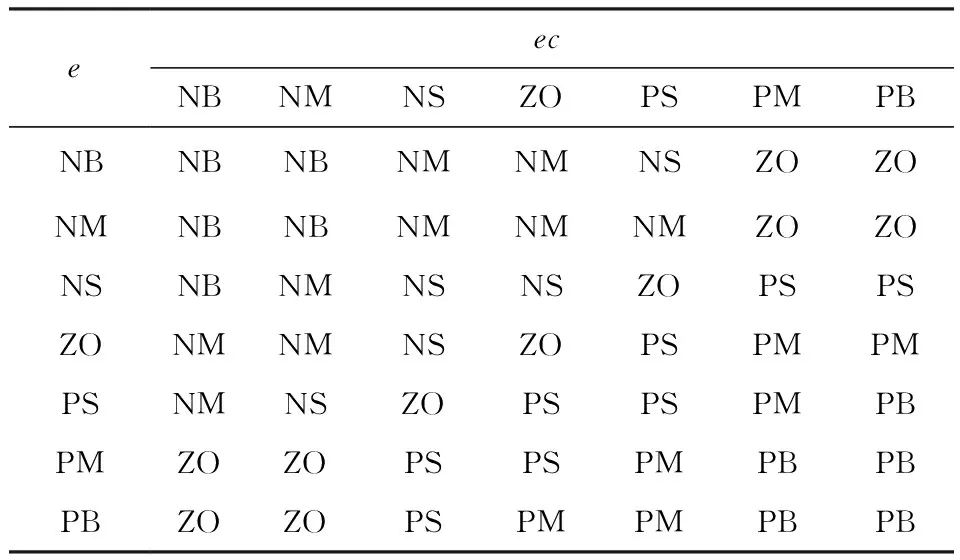
表2 ΔKi的模糊控制规则Tab.2 Fuzzy rule control of ΔKi

表3 ΔKd的模糊控制规则Tab.3 Fuzzy rule control of ΔKd
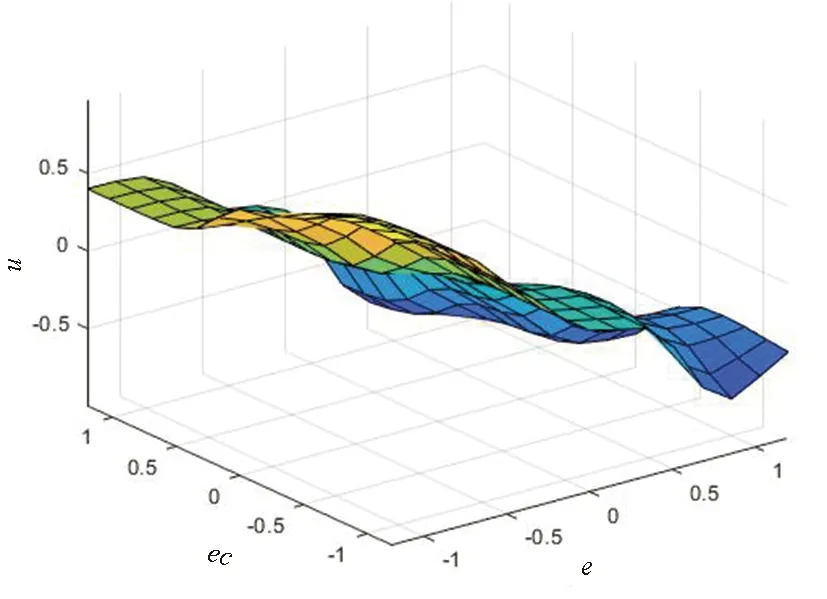
(a)Kp模糊控制规则图
2 转向执行电机控制策略的建模与仿真分析
根据设计的电机控制策略,在MATLAB/Simulinks仿真平台上进行建模。电机参数见表4。

表4 PMSM主要参数Tab.4 Main parameter of PMSM
直流母线电压为24 V,PWM波的周期为0.000 1 s,转子电角度初始值为θ=0°,三相电流初始值为0。主要进行恒定转矩时正弦位置输入和斜坡位置输入情况下输出转角与给定转角位置跟踪的两种仿真分析,通过位置跟踪效果对系统的稳定性和快速性进行评价。
图6和图7为三相电流仿真波形图,从图中可以看出,在0.5 s和1.5 s,三相电流完成相位变化。图8为电磁转矩仿真图,从图中可以看出,在速度环控制中,普通PID控制的电磁转矩在0.3 s以前波动明显高于采用模糊PID控制。图9是转子位置图,从图中可以看出,所设计的模糊PID和普通PID都能很好地跟随给定值的输入。但从图10位置误差图中可以看出,所设计的模糊PID抖动现象很轻,在快速跟随的同时保证了其稳定性,而普通PID最大有0.1 rad/s的抖动,说明所设计的模糊PID控制系统稳定性更好。

图6 普通PID三相电流(正弦信号输入)Fig.6 Common PID three-phase current (sinusoidal signal input)
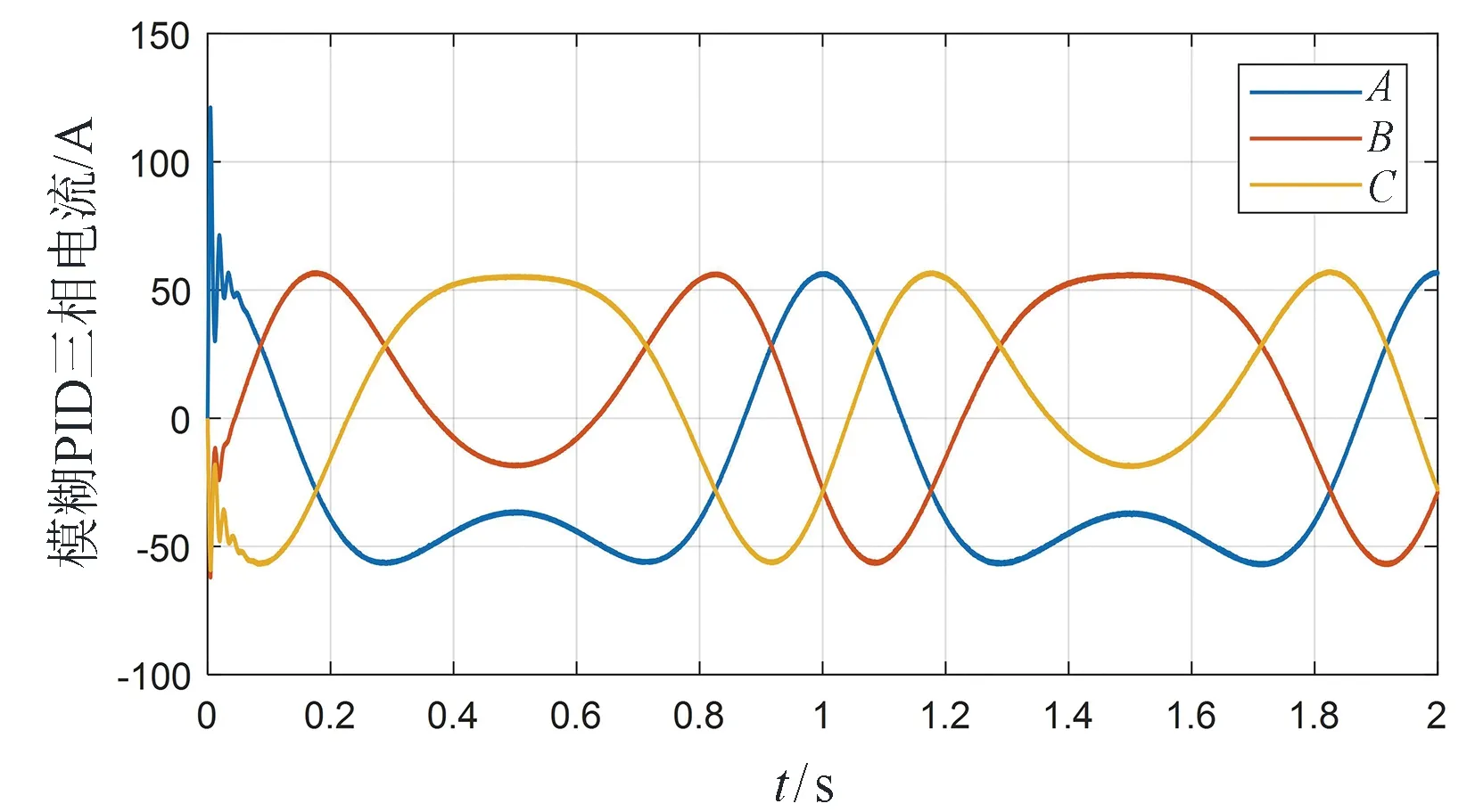
图7 模糊PID三相电流(正弦信号输入)Fig.7 Fuzzy PID three-phase current (sinusoidal signal input)
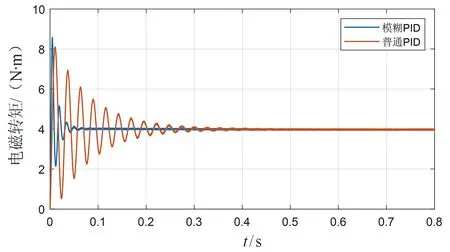
图8 输出电磁转矩(正弦信号输入)Fig.8 Output electromagnetic torque (sinusoidal signal input)
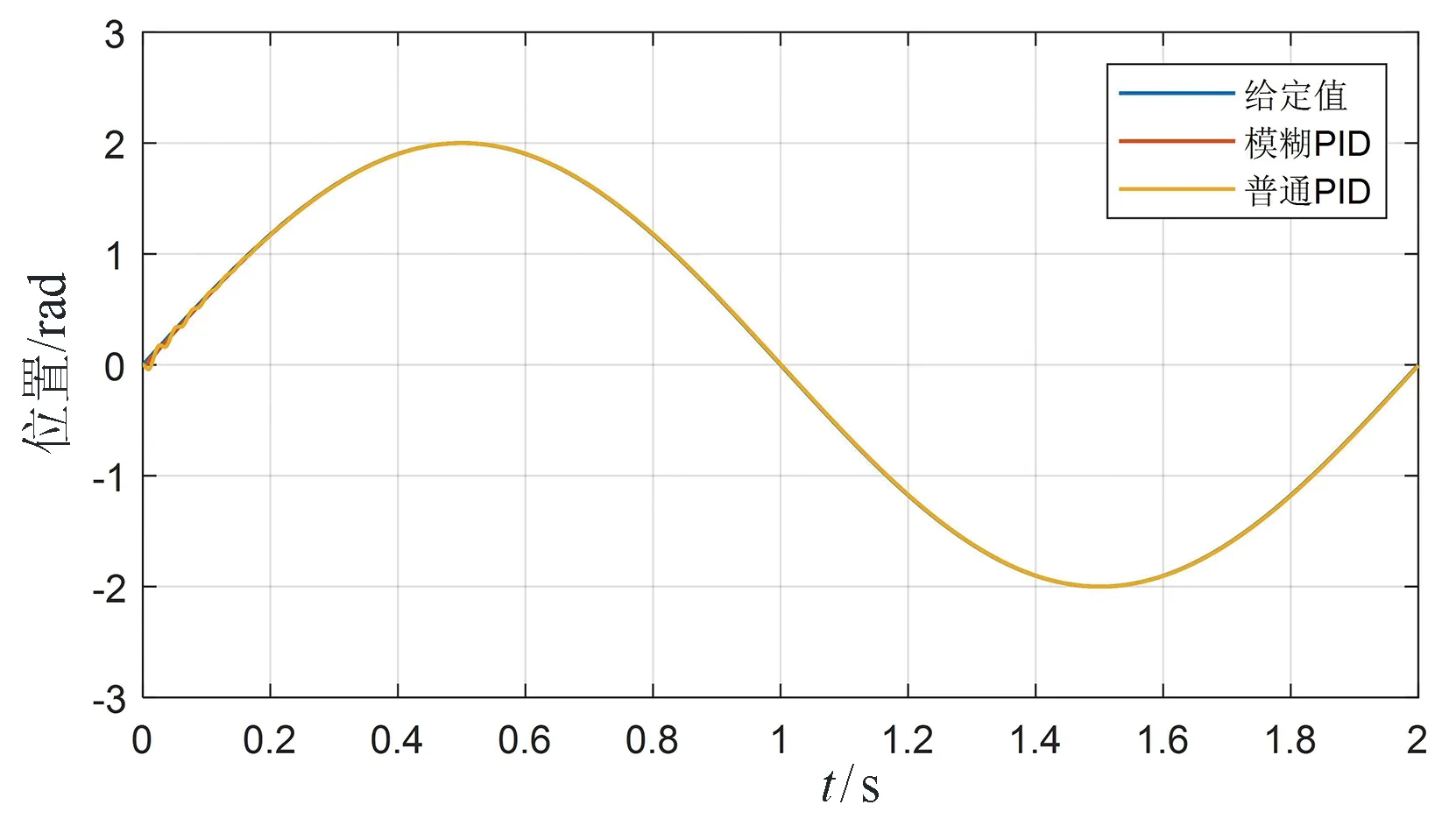
图9 位置跟踪(正弦信号输入)Fig.9 Position tracking (sinusoidal signal input)
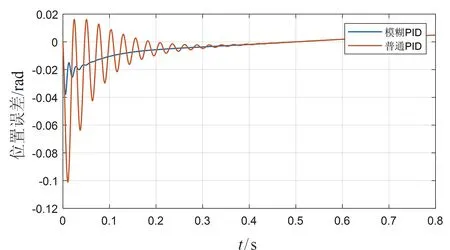
图10 位置误差(正弦信号输入)Fig.10 Position error (sinusoidal signal input)
图11和图12为三相电流仿真波形图,从图中可以看出,在三相电流相位变化过程中,电流值达到稳定值之前普通PID控制的抖动比模糊PID大。图13为电磁转矩仿真图,从图中可以看出,速度环采用模糊PID控制与采用普通PID控制相比,采用普通PID控制的电磁转矩在0、0.4、1.6 s斜坡信号发出时都产生了较大波动。图14为转子位置图,从图中可以看出,所设计的模糊PID和普通PID都能很好地跟随给定值的输入。但从图15位置误差图中可以看出,在0、0.4、1.6 s发出斜坡信号时,所设计的模糊PID抖动现象很轻,在快速跟随的同时保证了其稳定性,而普通PID最大有0.02 rad/s的抖动,说明所设计的模糊PID控制系统稳定性更好。
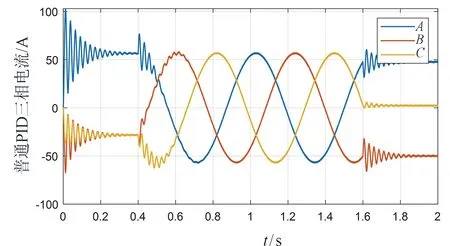
图11 普通PID三相电流(斜坡信号输入)Fig.11 Common PID three-phase current (ramp signal input)

图12 模糊PID三相电流(斜坡信号输入)Fig.12 Fuzzy PID three-phase current (ramp signal input)

图14 位置跟踪(斜坡信号输入)Fig.14 Position tracking (ramp signal input)
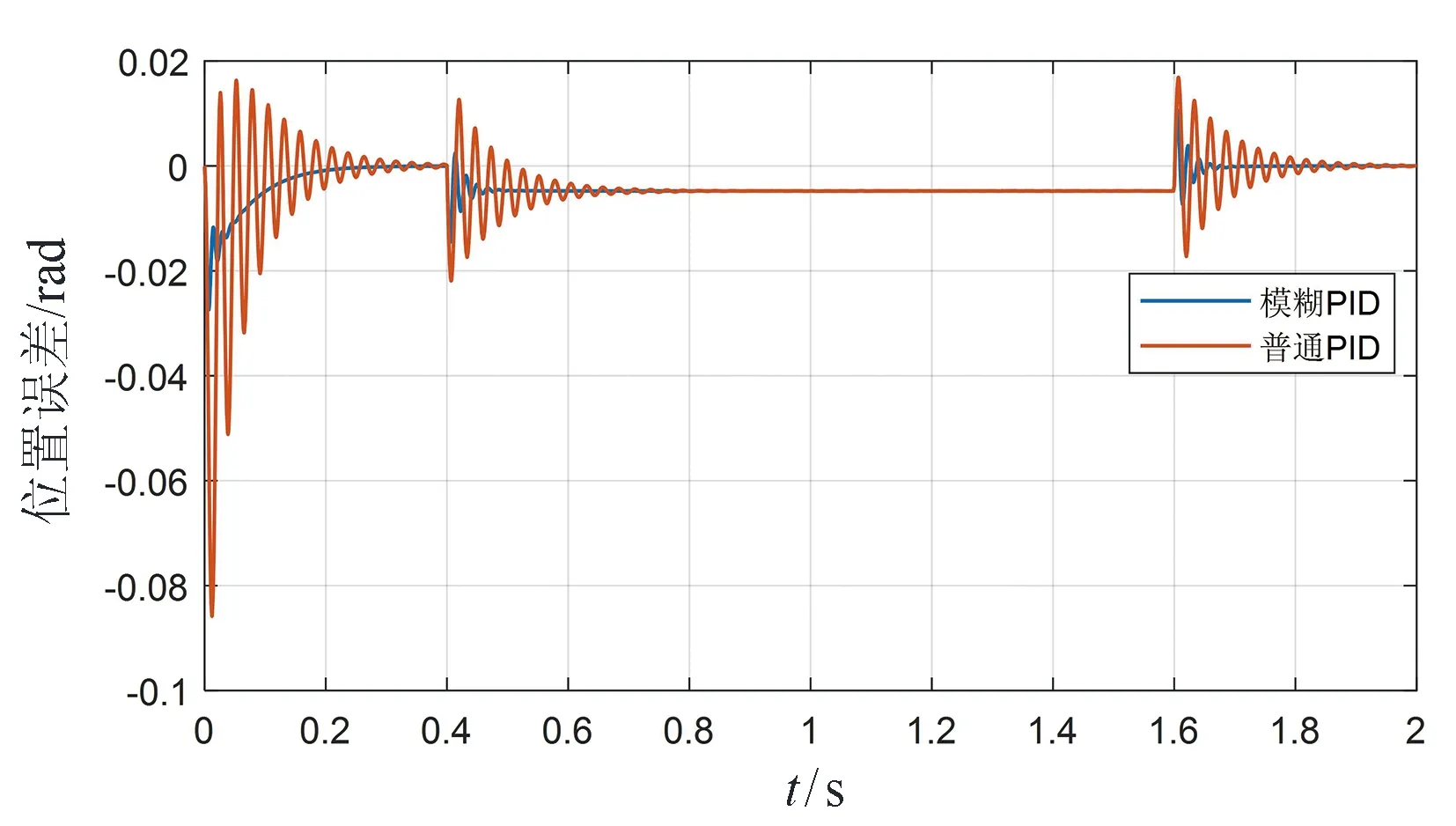
图15 位置误差(斜坡信号输入)Fig.15 Position error (ramp signal input)
3 结论
1)系统采用基于模糊控制的三闭环控制策略,保证电磁转矩在工况发生改变时,能够快速趋于稳定状态,且总体抖动误差比传统控制低2 N·m,符合叉车在要求转矩快速响应的同时也能够快速达到稳定的要求。
2)系统采用基于模糊控制的三闭环控制策略,实现了输出转角在快速跟随给定转角的同时,保证了其稳定性,且相比于传统控制,当工况发生改变时,正弦工况最大有0.1 rad/s的抖动,阶跃工况最大有0.02 rad/s的抖动,说明所设计的模糊PID控制系统稳定性更好,符合叉车转向电机位置环精确控制且在较短时间完成动态调节的要求。
3)仿真结果整体表明了所设计的三闭环控制策略拥有较好的快速性和稳定性,且位置跟踪延时小,可以满足叉车线控转向系统对转向执行电机的控制需求。

