船舶碎冰区横荡运动的水动力导数研究

王 超，刘 正，朱江波，汪春辉，郭春雨

（1.哈尔滨工程大学船舶工程学院，哈尔滨 150001；2.中国舰船研究设计中心，上海 201108；3.启东中远海运海洋工程有限公司，江苏启东 226200）

0 引 言

船舶水动力导数表示船舶以某一速度运动，保证其他运动参数不变的情况下，只改变某一个运动参数所引起的船体所受水动力的改变与运动参数的比值。船舶水动力导数与合适的水动力模型相互配合能够很好地预测船舶在航行时所受到的阻力以及力矩，避免了大量的实船以及船模实验测量工作，从而节省了大量的人力以及物力。水动力导数研究具有实际性，通常针对某一类型船舶进行研究，不同类型的船舶测量得到的水动力导数相差较大，水动力导数的研究具有复杂性以及针对性。水动力导数的研究方法主要存在经验公式法、约束船模试验法和数值模拟方法等。其中，约束船模试验是目前公认的求解水动力导数较为准确的方法。海军工程大学吴兴亚等[1]针对民用打捞型船采用CFD 软件STAR-CCM 模拟了敞水中船舶纯横荡运动，将其结果与理论公式进行对比，验证了CFD 方法求解水动力导数的可行性，说明了使用该软件进行计算存在一定的依据。上海交通大学楼鹏宇[2]采用FLUNT软件针对KVLCC1船型进行了限制水域的纯横荡运动数值模拟，忽略了自由液面的影响，进行了不同的水域宽度以及深度下船舶水动力导数影响研究，为限制航道船舶操纵性提供了安全指导。Miller 等[3]使用了CFDSHIP-IOWA 程序对船舶斜航、横荡、艏摇等数值模拟的RANS 方程进行了求解，得到了部分水动力导数。Turnock 等[4]对船模KVLCC2 进行了横荡运动的流场以及水动力数值模拟，将计算结果与实验进行了对比，较小的误差验证了数值手段的合理性。Stern 等[5]在国际会议SIMMAN 2008 的基础上总结了目前数值模拟船舶操纵性的CFD 手段以及提出采用DES 方法时更细网格可以给出更为精确的结果。Cura-Hochbaum 等[6]对KVLCC1 进行了基于RANS 方法的PMM 运动数值模拟并将求解的水动力导数代入操纵预报方程进行了运动轨迹预报对比，验证了RANS 方法的可靠性。Kim 等[7]采用基于DSGS 模型的求解器SHIP_Motion，研究了KCS 船模的纯横荡以及纯艏摇试验，数值计算水动力导数结果与实验结果吻合较好，说明CFD 手段可以替代实验研究水动力导数。Yoon等[8-9]基于水面舰艇DTMB 5415，采用自主开发程序CFDShip-Iwoa 进行了PMM 试验数值模拟，将数值预报得到的相关的水动力导数与试验结果进行对比分析，大部分线性水动力导数数值预报精度较高，非线性水动力导数预报误差较大。由此可以看出，非线性水动力导数预报仍然存在较大的难度，由于计算时非线性水动力导数引起的阻力部分不容易被捕捉，进行数值计算时要着重考虑该部分的计算手段。Kim等[10]以及Vroegrigk[11]分别应用有限元软件LS-DYNA 以及STAR-CCM+软件，模拟了船舶在碎冰航道中航行时相关性能，并针对冰阻力进行了研究，但是上述两位学者在研究冰船相互接触时，只进行了单项耦合设置并未涉及双向耦合，也没有对水动力进行相关研究。Lau等[12]使用离散元手段针对海冰与船舶作用下破碎模型以及船舶阻力进行了研究，证明了离散元方法在研究海冰与船舶等结构物的碰撞是可行的，也为后续采用DEM 方法模拟海冰提供了一定的思路以及方法。杨勇[13]等通过求解非定常RANS方程对KVLCC1裸船体在深水以及浅水中进行了纯横荡运动数值模拟，计算了相关的力和力矩，忽略了自由液面影响，得出了船舶在浅水中所受到的水动力以及线性水动力导数远大于深水中相应数值的结论，证实了船舶的浅水效应。刘晨飞等[14]运用CFD 以及重叠网格技术模拟了斜航和纯横荡运动，分别计算了月池封闭以及打开时的船舶水动力导数，得到了水动力导数会因为月池存在而有所增加的结论，证明了使用重叠网格在计算船舶水动力导数时具有一定的准确性，可用于控制船舶运动进行水动力导数求解。哈尔滨工程大学郭春雨等[15]使用LS-DYNA 软件模拟了船舶碎冰阻力以及船-冰作用过程，在较低速度条件下得出数值模拟结果在定性上与试验结果比较符合,数值计算方法研究船舶与碎冰相互作用具有一定的可行性。季顺迎等[16]运用改进型DEM模型模拟冰的运动变化过程，并将此方法应用于船-冰作用及海洋结构物-冰作用上，针对密集度、流速、冰块尺寸以及厚度对冰阻力的影响进行了研究，得出了海冰参数的增加均会导致海冰对船体的冲击动量以及频率增加的结论，尽管该研究在浮冰形态、船体性能以及流体动力方面进行了诸多假设，但是计算方法以及思路具有较大的参考意义。涂勋程[17]使用软件LS-DYNA 在浮冰环境和平整环境下对物探船的冰阻力预报及相关参数敏感性开展了数值模拟研究。王超等[18]运用离散元模型结合欧拉多相流，对船体与碎冰之间的相互作用关系进行了探索，得出以下结论：船体所受冰阻力主要是由碎冰与船体表面的摩擦和碰撞产生，并随航速的增大而增大，但当航速增大到一定值后，碎冰阻力不再增加，甚至还有减小的趋势。

碎冰区冰水耦合下船舶水动力导数的研究较少，目前研究人员考虑冰水耦合主要针对于碎冰存在水浮力时碎冰阻力以及独立的水阻力研究，并未考虑耦合后对流体阻力本身的影响。本文拟采用STAR-CCM+软件中DEM模块下的双向耦合模式对碎冰区中某型船舶进行不同运动频率下的纯横荡运动模拟，求取船舶所受的侧向力以及转艏力矩，进而经无因次化求解出冰水耦合下的部分水动力导数，为今后考虑耦合下流体增阻后的水动力导数以及操纵性能预报方法研究提供理论基础和技术支撑。

1 基础理论和计算模型

本研究采用STAR-CCM+软件。湍流模型选择标准k-ε模型，依靠STAR-CCM+中DEM 模块下的双向耦合功能达到冰水耦合作用，该耦合模式考虑了离散相对连续相的影响，主要包括位移、相间动量、质量以及热传递的影响。由拉格朗日离散相方程对网格单元进行积分可得出每个颗粒的动量、质量以及能量的变化。通过对穿透体积的所有颗粒进行求和，从而得到网格单元内与连续相交换的总的动量、质量和能量，将其代入连续相方程从而得到冰块与水的相互耦合作用。使用STAR-CCM+软件中重叠网格使船模具有横向运动y=asin（ωt），从而模拟船模横荡运动，监测耦合后船舶所受的水动力。

1.1 DEM基础理论

本文采用STAR-CCM+中DEM 模块模拟碎冰粒子。碎冰是由若干基本颗粒组成的DEM 粒子，在拉格朗日构架下，通过显式计算跟踪计算域中所有粒子的轨迹。CFD-DEM 耦合计算主要包括离散相冰之间的相互作用以及离散相冰与流体性水之间相互作用的计算。离散相DEM 冰粒子的运动通常包括平行运动和转动运动两种方式，需满足平动动量守恒以及旋转角动量守恒方程，具体形式如公式（1）和（2）。

离散相DEM 冰粒子平动运动动量守恒方程为

离散相DEM冰粒子旋转运动角动量守恒方程为

式中，mi、vi和wi分别表示离散冰项粒子编号i的质量、速度和角速度；Ii为编号i的粒子的转动惯量，Ri为粒子i的半径；Fg=mig为粒子i的重力；Ffluid为流体对粒子i的作用力；Fij为粒子i与粒子j或壁面之间的碰撞力以及其他作用在粒子上的非接触力；Tij为接触力矩，表示除粒子重力以外的接触力在粒子上产生的扭矩。

1.2 重叠网格

在涉及到物体自由运动的求解计算中，重叠网格具有较大的优势。重叠网格是由Steger在上世纪50 年代提出的，最大的特点是不同的区域网格交界能够发生重叠、嵌套和覆盖等拓扑关系，能够明显减小网格生成的难度，且生成的网格具有较高的质量，对复杂形状的适应性很强。在重叠网格中，不同区域的相对位置关系可以随时间变化。在模拟的过程中，重叠网格之间节点的数据是根据插值计算来进行的。重叠网格各个子区域之间的相互作用关系往往是通过三个步骤来实现的：定义区域网格、搜索贡献单元以及网格之间的数据插值。

1.3 数学模型的建立

单一来说，冰粒子主要属于固体力学研究范畴，流体力部分属于流体力学研究范畴，运用STARCCM+中DEM 模块模拟碎冰粒子，DEM 参数的设置具有开放性，可进行变参数研究。横荡运动存在两部分流体域，其中运动域如图1所示，该运动域用于控制船体做y=asin（ωt）运动。计算域如图2所示，为模拟无限水域减少池壁效应，计算域速度入口距离船首部3L，压力出口距离船尾部3.5L，左右两侧距离船中3.3L，顶部以及底部分别距离船舶2L、3.5L。

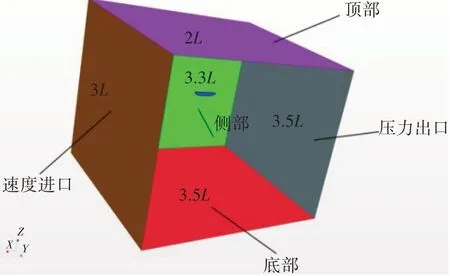
图2 计算域Fig.2 Computational domain

1.4 船体及碎冰模型的建立

碎冰区冰块厚度范围在0.3～3 m 左右[17]，小型碎冰跨度在2 m 左右，大型浮冰尺寸跨度为0.5～10 km[17]。模拟采用的碎冰粒子是用DEM 复合颗粒去填充形成，尺寸过大会造成喷射碎冰粒子耗时长。综合考虑，本次碎冰模型采用小型碎冰，长度、宽度、厚度分别为3 m、3 m、1.5 m，按缩尺比1：40进行建模。冰粒子如图3 所示，碎冰的粒子填充数为120，采用STAR-CCM+软件中探针进行碎冰喷射，其中探针的长度为6 m，分辨率为38，如图4所示。船模主尺度以及碎冰物理参数列于表1中，表中碎冰的物理参数指的是依据实尺度冰属性与缩尺的关系换算得到的模型冰参数。

图3 碎冰粒子图Fig.3 Brash ice particle

图4 探针布置图Fig.4 Probe layout

表1 某冰区船型参数及碎冰物理参数Tab.1 Ship type parameters of ice region and physical parameters of brash ice

1.5 带有重叠网格的计算域网格划分

网格划分模型选用切割体网格、棱柱层网格以及表面重构。总体网格基础尺寸为2.3%L，船体表面网格大小选取为基础尺寸的12.5%，船舶尾部进行网格加密，尺寸为基础尺寸的6.25%，棱柱层总厚度为0.025 m，棱柱层数为6，棱柱层延伸率为1.2。船体网格如图5（a）所示，尾部网格加密如图5（b）所示。由于DEM 粒子的求解是否收敛很大程度上取决于水线面x-y-z向网格密度，分别对自由液面进行x-y-z向加密，z向采用两层加密，网格尺度分别为基础尺寸的25%、12.5%。x-y方向网格尺度均为基础尺寸的80%。计算域整体网格图如图5（c）所示，z向加密如图5（d）所示。考虑重叠网格自身的属性，将运动域外表面网格尺寸定为基础尺寸的40%，同时计算域采用两层过渡，计算域最后一层网格尺寸也为基础尺寸的40%，达到运动域表面的重叠网格要尽量与背景网格贴合。运动域与背景网格贴合如图5（e）、（f）所示。重叠网格迭代方式为线性迭代。

图5 网格划分图Fig.5 Distribution of meshes

2 计算方法的验证

数值计算方法的验证依托哈尔滨工程大学船模拖曳水池中进行的76K 冰区加强散货船[19]的碎冰试验。76K 船模网格以及DEM 相关设置与本文破冰船数值模拟设置一致，通过验证76K 数值模拟的网格以及DEM 设置的合理性从而验证本次数值模拟方法的准确性。本次验证选择一种碎冰密集度60%、一个航速点0.613 m/s，进行敞水船模阻力、碎冰阻力以及碎冰姿态验证。实验采用的碎冰尺寸具有随机性，存在多种大小不同的碎冰，数值模拟时如果采用多种碎冰容易造成冰水耦合求解发散，极大地消耗计算资源，并且不同的碎冰尺寸所需要的网格设置不同，采用多种碎冰需要在一次计算时设置不同的计算网格。文献[16]曾说明海冰密集度以及厚度保持不变的情况下，冰块尺寸的变化主要改变冰块与船体的碰撞频率，平均阻力变化不明显。基于上述原因，本次数值模拟中碎冰厚度采用与实验中碎冰相同厚度，数值模拟碎冰长宽尺寸选择与实验中碎冰尺寸比较小的一类相一致。图6（a）中静水阻力数值模拟值取后5 s 均值为5.32 N，静水阻力实验值为5.19 N，误差为3%；图6（b）中碎冰阻力图中数值模拟碎冰阻力值均值为4.89 N，实验值为4.33 N，误差为13%。使用重叠网格时，背景网格与重叠网格之间进行网格信息的传输时不可避免地会发生些许信息的丢失，所以阻力部分的误差将会偏大，但误差仍处于可接受范围之内。从图7 中可以看出，76K 冰区加强散货船以及某型破冰船的数值仿真结果与76 K 试验结果在船舶尾部均出现了碎冰沿着船两侧移动最后在船尾形成的尾迹。从图8中可看出，76K冰区加强散货船以及某型破冰船的数值仿真结果与76K试验结果在船舶首部均出现了碎冰堆积现象，并且沿着船首向船两侧移动。综上所述，本次数值模拟具有一定的准确性，可以较为真实地模拟船舶在碎冰区航行时相关的阻力性能以及冰块运动姿态。

图6 76K冰区加强散货船碎冰区阻力Fig.6 Resistance of ice strengthened 76k bulk carriers in floe ice region

图7 尾部区域碎冰分布图Fig.7 Floe ice distribution at the stern area

图8 船艏碎冰运动姿态图Fig.8 Floe ice motion posture at the stem area

3 计算结果及分析

3.1 数值求解方法

求解方法如下：公式（3）为船舶水动力计算公式，其中Yv、Nv为线速度导数即位置导数，Yv̇、Nv̇为线加速度导数。对公式（3）进行无量纲化得公式（4）。

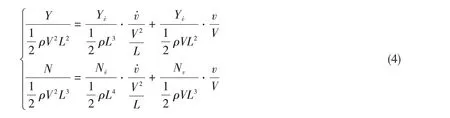
将船舶纯横荡运动条件代入公式（4），得

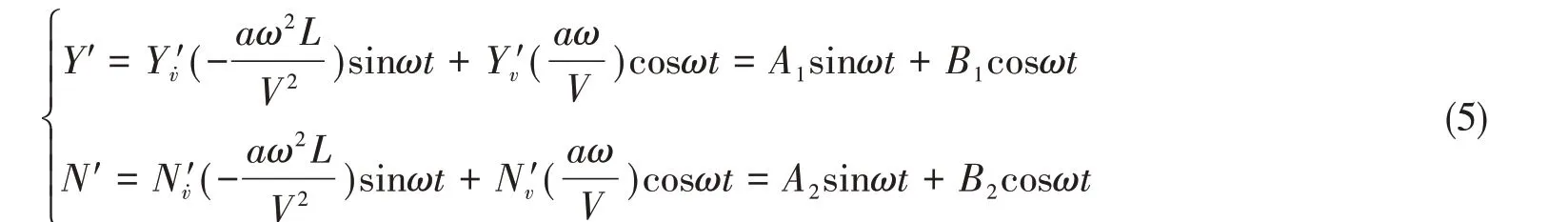
式中，A1、A2、B1、B2分别为

只需要对各横向力和力矩曲线进行非线性曲线拟合，得到y=asinωt+bcosωt的形式，即可得出系数A1、A2、B1、B2，从而得到船舶的水动力导数。

3.2 敞水工况横荡运动水动力导数数值计算结果

纯横荡运动选择频率f分别为0.06 Hz、0.08 Hz、0.1 Hz、0.12 Hz和0.14 Hz，考虑冰区船舶在航行时运动幅度变化不大，按照40缩尺后船模的运动振幅为a=0.075 m，采用重叠网格方法建立运动域，将运动y=asin(wt)赋予船体，同时设置来流速度V=0.8 m/s。分别监测各个频率下船舶所受的侧向力Fy以及转艏力矩Nz，如图9和图10所示。通过ORIGIN软件进行各个频率下的横向力和力矩曲线拟合并将结果进行无量纲化，拟合系数列于表2 中。根据各非线性系数计算结果即可求得各频率下船模的横荡水动力导数，列于表3中。

图9 敞水工况横荡0.06～0.14 Hz船舶所受的侧向力Fig.9 Lateral forces on ships in open water conditions at 0.06-0.14 Hz

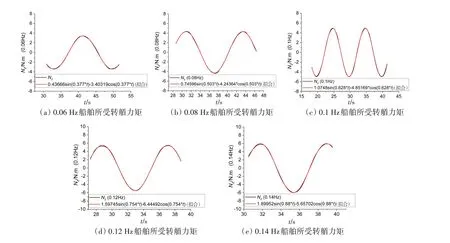
图10 敞水工况横荡0.06～0.14 Hz船舶所受的转艏力矩Fig.10 Turning moments on ships in open water conditions at 0.06-0.14 Hz

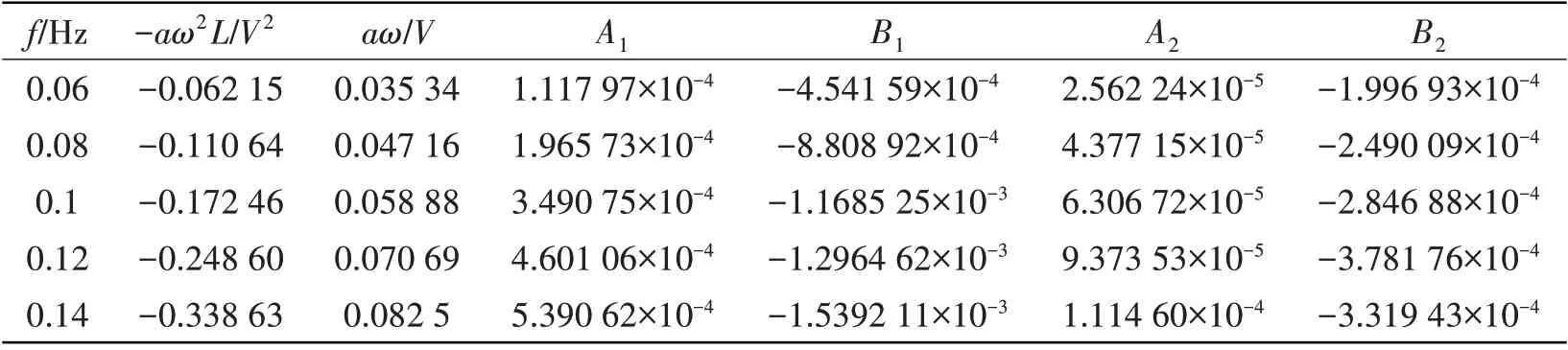
表2 各频率下非线性拟合系数A1、B1、A2、B2值Tab.2 Non-linear fitting coefficients of A1,B1,A2 and B2 at different frequencies

表3 V=0.8 m/s船模做纯横荡运动时水动力导数计算结果Tab.3 Hydrodynamic derivative calculation results of ship model performing pure sway motion at V=0.8 m/s

从图9、图10 中可以看出，敞水工况船舶的转艏力矩以及侧向力都随着频率的增加而增大，符合理论推导。井上模型[20-21]统计公式求得水动力导数Y'v=0.016 5，N'v=0.005 8。由表3 可知，敞水工况下数值模拟的船舶水动力导数与统计公式相差不大，其中水动力导数Y'v平均误差较统计公式偏差小，水动力导数N'v平均误差大。这是由于当船模处于横荡运动模式时，改变频率对船舶所受侧向力的变化较转艏力矩的变化更为敏感，从而导致水动力导数Y'v预报更接近统计值。并且统计公式采用的是井上模型，井上模型是根据10 艘各种类型的船模（油轮3 艘，货船3 艘，集装箱船、液化天然气船、滚装船、汽车轮渡各1 艘）进行相关的PMM 运动试验整理出的水动力导数计算公式，本次计算模型采用的是冰区某型破冰船，其型线以及舱室布置、尾部形状都进行了改进，与传统船型存在一定的差别，所以一定意义上导致了水动力导数N'v平均误差大。

3.3 碎冰工况冰水耦合后水动力导数数值计算结果

碎冰工况下船舶运动参数设置与敞水工况一致，即频率f分别为0.06 Hz、0.08 Hz、0.1 Hz、0.12 Hz和0.14 Hz，运动振幅为a=0.075 m。考虑计算耗时问题，本次模拟碎冰密集度较低为60%，经调研某型破冰船在浮冰工况下（浮冰尺寸大于50～60 cm），连续破冰航速是连续自破冰下航速不超过10 kn，0.2～0.3 m的浮冰基本不受影响，考虑本次模拟情况为低密集度小型碎冰并且不存在破冰船引航，选取船舶速度为9.8 kn，依据傅汝德数相似换算来流速度为0.8 m/s。同时将船体表面设置为壁面，物理模型选择拉格朗日多相模型中的多相耦合模型。多相相互作用设置冰-冰接触、冰-船接触、冰-水接触、冰-空气接触、水-空气接触。通过冰-船耦合作用改变冰块运动姿态进而冰块对船体周围流场产生干扰从而达到船-冰-水相互耦合。滚动阻力模型选用Hertz Mindlin，阻力系数模型使用Schiller-Naumann模型。各个频率下船舶所受的侧向力Fy以及转艏力矩Nz如图11～12所示。对于各频率下的横向力和力矩拟合后得到的系数列于表4中，求得的各频率下船模的纯横荡水动力导数值列于表5中。

图11 碎冰工况横荡0.06～0.14 Hz船舶所受的侧向力Fig.11 Lateral force on ships in floe ice area conditions at 0.06-0.14 Hz

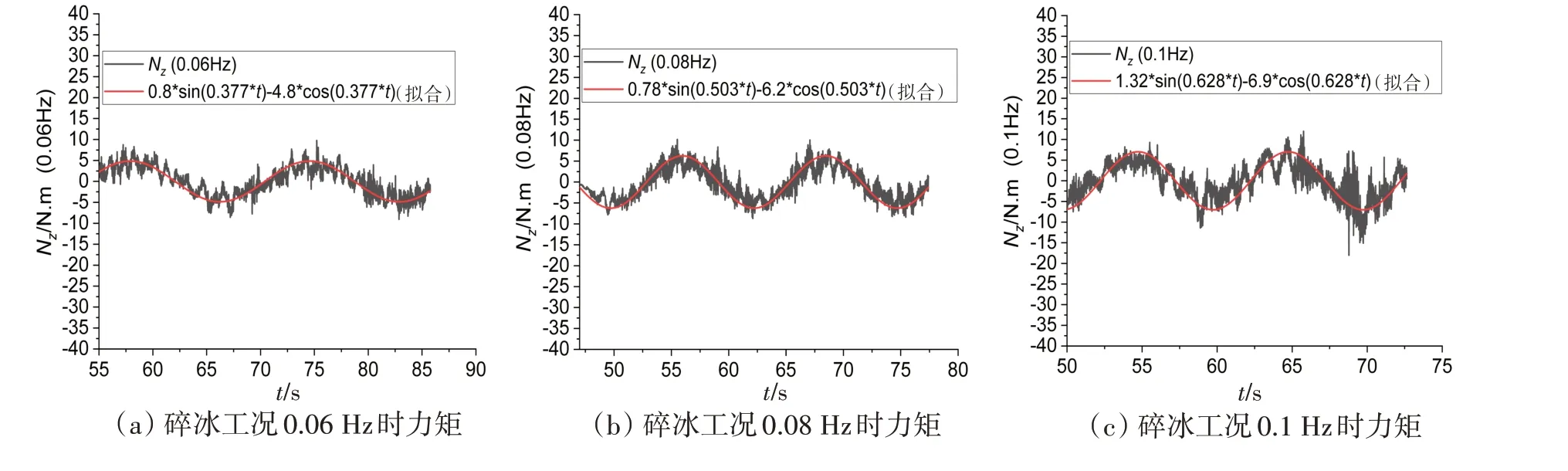
图12 碎冰工况横荡0.06～0.14 Hz船舶所受的转首力矩Fig.12 Turning moment on ships in floe ice area conditions at 0.06-0.14 Hz

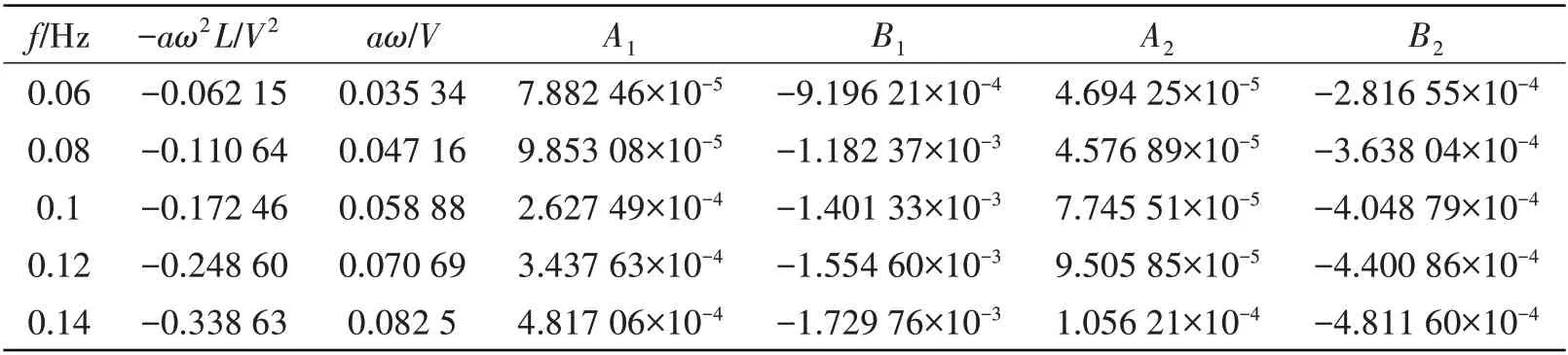
表4 各频率下非线性拟合系数A1、B1、A2、B2值Tab.4 Non-linear fitting coefficients of A1,B1,A2 and B2 at different frequencies

表5 V=0.8 m/s船模做纯横荡运动时水动力导数计算结果Tab.5 Hydrodynamic derivative calculation results of ship model performing pure sway motion at V=0.8 m/s

从图11～12 中可以看出，冰水耦合下船舶的侧向力以及转艏力矩都呈现上下波动趋势。这是由于碎冰与船舶碰撞时，运动姿态发生改变，部分会堆积在船舶周围，部分会沿着船体表面滑行、翻转，还有极少数的冰块会贴在船体随船舶一起运动。这些冰块不确定的运动扰动了船体周围流场，从而对船舶的水动力产生上下波动的情况。表5中船舶水动力导数Y'v、N'v比敞水工况值偏大，由此可以判断冰水耦合下由Y'v、N'v所引起的船舶流体阻力将会增加。耦合后Y'v、N'v水动力导数值较敞水工况值偏大，主要原因在于船舶在碎冰中航行时，冰块与船体相互作用具有随机性导致碎冰运动姿态同样具有随机性，随机运动的碎冰对船体周围的流场扰动不规则，扰动了船体周围的边界层，增大了船舶航行时所受的阻力。表5中低频率时船舶的水动力导数Y'v̇、N'v̇明显大于敞水工况下水动力导数值，当频率大于0.1 Hz时冰水耦合后水动力导数值增加不明显，主要原因在于随着频率的增加，船舶周围的流场变化剧烈，压力差明显，冰块更容易贴在船体表面，贴在船体表面的碎冰使得水流与船体接触变少，导致了冰水耦合后在较高频率时水动力波动减弱，形成了冰水耦合时低频率水动力导数值要明显大于敞水工况值的现象。但是Y'v̇比敞水工况值偏小，这是由于船舶在航行过程中冰块对船体的碰撞力是一个瞬时阻碍船舶运动的力，所以冰碎耦合后船舶的加速度较敞水工况值偏小，加速度部分引起船舶的阻力占总的水阻力分量将会减小，从而导致了Y'v̇比敞水工况值偏小。水动力导数N'v̇与敞水工况值总体上相差不大，这是由于船舶横向加速度在船舶转艏力矩中灵敏度偏低，船舶的转艏力矩主要由N'v引起。随着运动频率的增加，部分碎冰会贴在船体两侧，将船体与周围的流场隔离开，水动力波动减弱，更不易捕捉船舶横向加速度在船舶转艏力矩中的变化，所以此项水动力导数值与敞水值偏差不大。

4 结 论

本文使用STAR-CCM+软件进行了碎冰区船舶横荡运动数值模拟，求解出敞水以及冰水耦合下船舶横荡运动时的水动力导数，所得结论如下：

（1）通过静水阻力、碎冰阻力以及碎冰与船舶艏尾运动姿态与实验结果对比，验证了本文数值方法的有效性。

（2）由于冰块与船发生碰撞作用时冰块的运动姿态和轨迹发生变化，造成船舶的侧向力以及转艏力矩在冰水耦合的情况下都呈现了上下波动的情况。

（3）碎冰工况下考虑冰水耦合船舶水动力导数Y'v、N'v、比敞水工况值偏大，而Y'v̇比敞水工况值偏小。

虽然本文使用CFD-DEM 方法在一定程度上解决了冰水耦合下横荡运动的水动力导数的求解问题，但还有许多设置需要改进，同时受到时间和计算能力等的限制，本文只计算了一种密集度下冰水耦合的情况，后期将针对不同密集度以及碎冰的不同尺寸部分进行研究。