竹材切割机械臂及关键零部件设计仿真
王慧,崔生乐,安洋,杨春梅
竹材切割机械臂及关键零部件设计仿真
王慧,崔生乐,安洋,杨春梅
(东北林业大学,哈尔滨 150040)
针对包装用竹材人造板制造中需要切割竹材的情况,设计一种无刷电机驱动的竹材切割机械臂,并设计其中往复锯的平衡机构,以平衡往复惯性力。对往复锯核心机构零件及内壳体进行强度校核,确保零件薄弱环节满足强度要求。在SolidWorks中建立往复锯机构及其平衡机构,通过Adams仿真验证平衡机构平衡效果。在Ansys软件中,对往复锯核心零件及其平衡机构进行有限元分析,求得其最大主应力以进行强度校核,最后设计完成主材切割机械臂的设计。Adams仿真表明往复锯剩余的往复惯性力极大值为7.564 2 N,平衡率为96.65%。Ansys有限元分析表明,各个零件的最大主应力最大值为70.645 MPa,远小于Q235许用应力值210 MPa。文中设计的竹材切割机械臂中的往复锯,经平衡机构平衡后,剩余往复惯性力较小,其核心机构零件及内壳体满足强度要求,主材切割机械臂设计满足要求。
机械臂;曲柄连杆机构;往复惯性力;强度校核
竹子广泛分布于亚洲等地,其生长周期短,更新周期快。在越来越重视环保的当下,竹子由于其优良的固碳能力及良好的材料性能越来越受到人们的重视。竹材是天然的薄壁中空筒体结构,限制了其使用。竹材人造板是重要的包装用材料,将竹材制成竹材人造板,有利于实现竹制品行业产业化发展。传统竹材人造板的制备有切断、破竹等过程,均需要对竹材进行切割。竹材最大直径约为150 mm,传统切割锯床多为圆锯,为顺利切割竹材需采用直径为380 mm的圆锯,这使得锯床体积过大,且更换圆锯成本增大;若锯床采用小直径圆锯,则需要圆锯运动为圆弧,增大了锯切运动机构的复杂程度,增大了锯床体积和制造成本。一般的,往复锯切割运动是锯片的往复运动,使得往复锯存在不平衡往复惯性力,因此,文中设计一种往复式竹材切割机机械臂,并设计其中往复锯的平衡机构,消除往复锯本身的往复惯性力,并进行仿真分析验证平衡效果,并进行关键零部件的强度校核。
1 双曲柄连杆机构分析及设计仿真
往复式竹材切割机械臂,其核心部分为电动往复锯。由于往复锯存在往复惯性力,锯及锯片产生周期性振动,因而用普通往复锯锯切的竹材断口不平整,存在毛边。此外往复锯的周期性振动还会产生NVH问题,导致往复锯机角架疲劳损耗,并降低了工人作业的舒适度[1-2]。为提高往复锯锯切竹材的平整度,提高竹材质量,并降低往复锯的NVH问题,需要从源头上抑制往复锯振动,因此,文中设计的竹材切割机械臂内的往复锯,应该带有平衡机构,抑制往复锯的往复惯性力,从而降低锯的振动,并最终提高竹材切割的质量。
1.1 双曲柄连杆机构分析
往复锯内部结构是曲柄滑块机构,当刀臂与曲柄连接处为圆弧滑槽时,机构等效为曲柄连杆机构。曲柄连杆机构运动不是正弦曲线,其加速度一般分解为一阶、二阶等。其中一阶、二阶往复惯性力计算见式(1)。

式中:为惯性力估值;为往复质量;为曲柄半径;为曲柄连杆比;为转速;为曲柄转过的角度。发动机曲轴、连杆、活塞、活塞销组成的机构是常见的曲柄连杆–滑块机构。以四缸发动机为例,当发动机点火顺序是1—3—4—2时,发动机1、2缸,3、4缸相互抵消一阶往复惯性力,1、4缸,2、3缸相互抵消全部往复惯性力矩,因而,当发动机连杆曲柄比大于2.5以上时,忽略曲柄连杆机构三阶及以上的往复惯性力,则丝杠发动机仅剩二阶往复惯性力。一般为降低NVH水平,提升车辆乘坐舒适性,四缸发动机配有转速为曲轴转速2倍的对向旋转的一对平衡轴,以平衡二阶往复惯性力[3-6]。
考虑往复锯,若刀臂上与曲柄连接处为圆弧滑槽时,机构等效为曲柄连杆机构时,需要采用2对平衡轴来平衡一阶、二阶往复惯性力,当刀臂上与曲柄连接处为直线滑槽时,刀臂运动曲线为正弦曲线,此时也需要1对对向旋转的平衡轴以平衡往复惯性力,平衡轴机构较为复杂,因此往复锯不宜采用平衡轴作为其平衡机构[7-9]。一种较好的平衡曲柄连杆机构往复惯性力的方法:采用等效双曲柄连杆机构,其中一个曲柄连杆机构驱动刀臂,另一个曲柄连杆机构驱动平衡质量;当刀臂与平衡质量质心在同一水平面内,且刀臂与平衡质量运动完全相同仅方向相反时,刀臂与平衡质量的全部惯性力可以互相平衡。如图1所示是曲柄连杆机构及双曲柄连杆机构简图,在双曲柄连杆机构中,2个曲柄连杆机构,运动方向相反[10-15]。
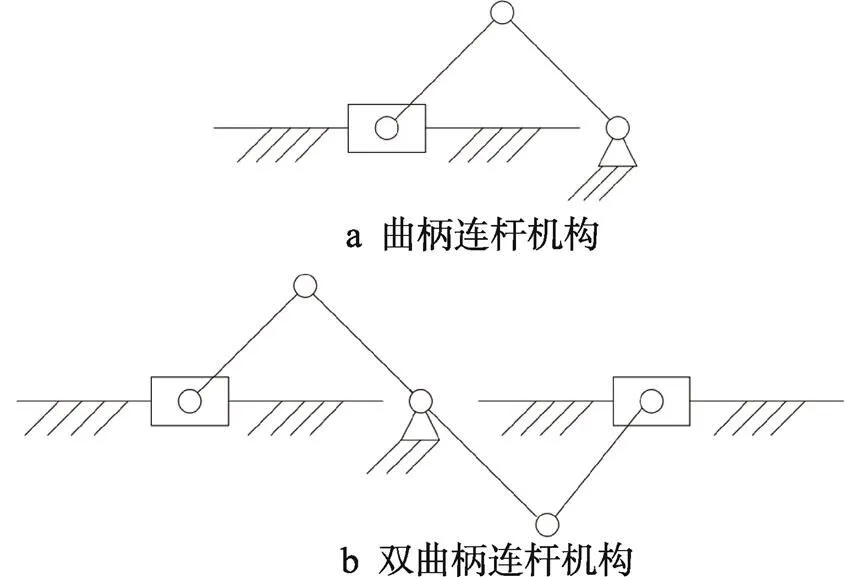
图1 曲柄连杆机构及双曲柄连杆机构
1.2 双曲柄连杆机构设计
根据平衡原理,在SolidWorks中建立机械臂核心机构模型见图2,机械臂核心机构由刀臂、上半曲轴、下半曲轴、平衡质量、2个滑动轴承和连接螺钉组成。其中,刀臂为2段材料焊接而成。为降低往复惯性力矩的产生,应当调整刀臂前臂相对后臂的位置以及平衡质量的质心,使两者质心尽量在同一水平面内。
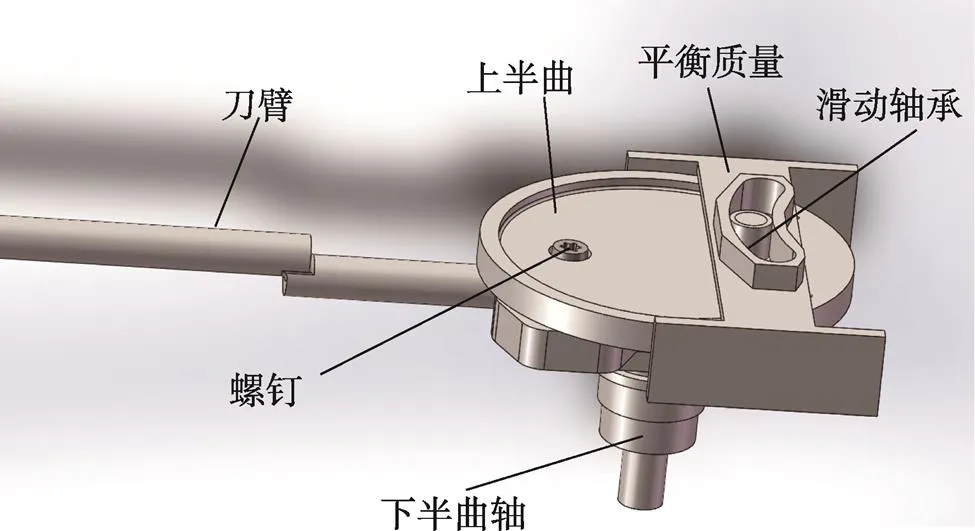
图2 机械臂核心机构
如图3所示是上半曲轴、下半曲轴和螺钉装配体。下半曲轴上有凸台,上半曲轴上有一空心凸台,曲轴间连接方式为铰链连接,螺钉的作用是将上、下曲轴连为一体,并传递扭矩。

图3 曲轴装配体
由于滑动轴承及凸台改变了曲轴的质量分布,当曲轴旋转时,会产生惯性力,因此,上、下曲轴上设计有偏心质量,以平衡滑动轴承及凸台产生的惯性力及力矩。刀臂、平衡质量、偏心质量的数据见表1。
往复锯等效的双曲柄连杆机构参数表2。
1.3 平衡效果验证
为验证设计后的往复锯平衡机构对往复惯性力的平衡效果,文中将在SolidWorks中建立的往复锯核心机构模型保存为Parasolid格式,并导入Adams软件,建立连接。普通往复锯的额定转速一般设定为3 000 r/min,为提高竹材切削效率,文中设定往复锯转速为4 200 r/min,并在Adams中设定曲轴驱动转速为4 200 r/min。Adams软件中求得的曲轴的惯性力及力矩曲线见图4,其中曲轴不平衡惯性力极大值为8.76 N,剩余的不平衡力矩为,其极大值为0.081 N·m。
表1 曲轴装配体各结构参数
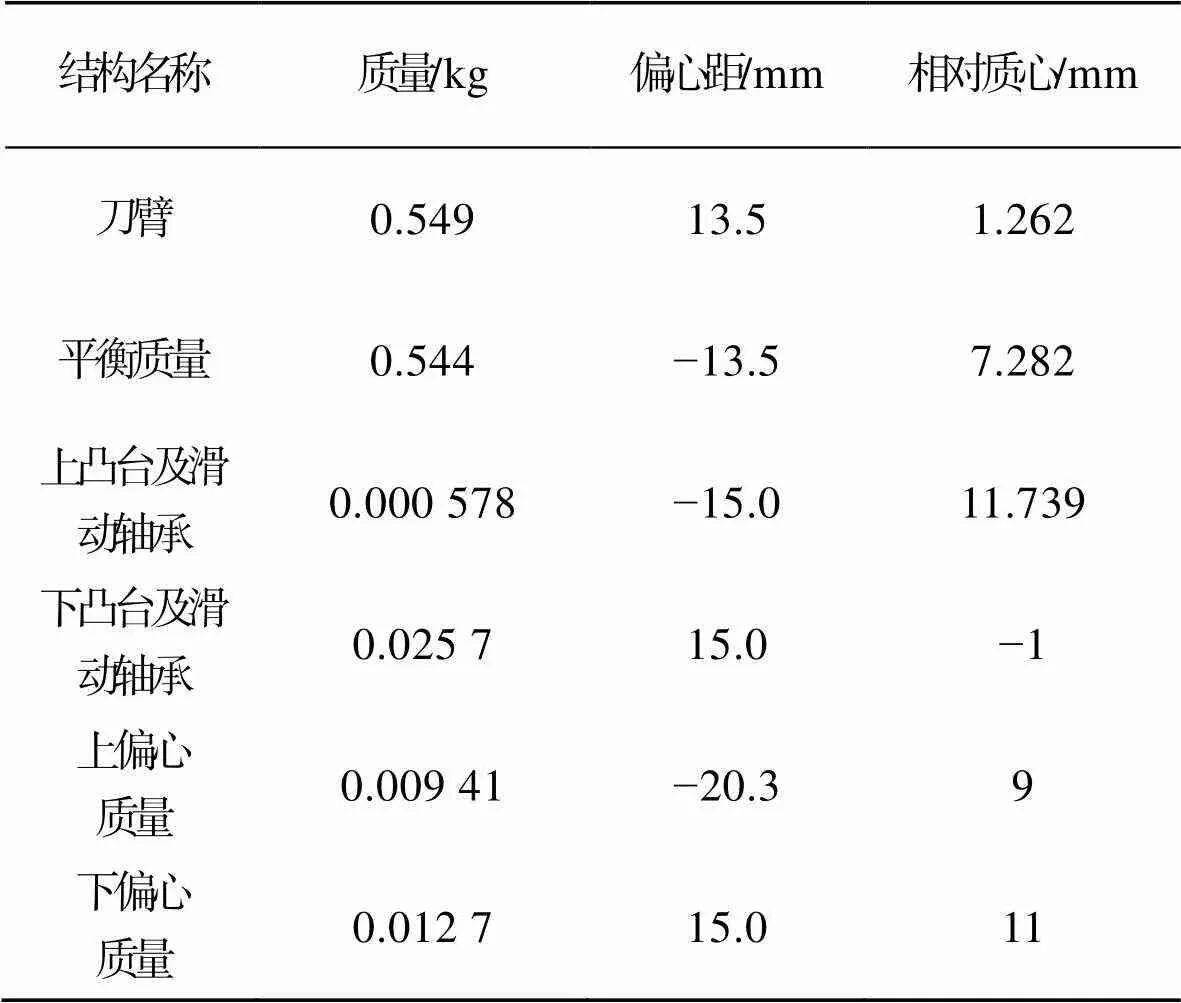
Tab.1 Structural parameters of crankshaft assembly
表2 双曲柄连杆机构参数

Tab.2 Parameters of double crank connecting rod mechanism
在Adams中求得的刀臂、平衡质量及平衡后的往复惯性力曲线见图5。其中,刀臂往复惯性力极大值为225.68 N,极小值为119.08 N。平衡质量的往复惯性力极大值为224.48 N,极小值为118.26 N,刀臂和平衡质量的往复惯性力数值基本相同。
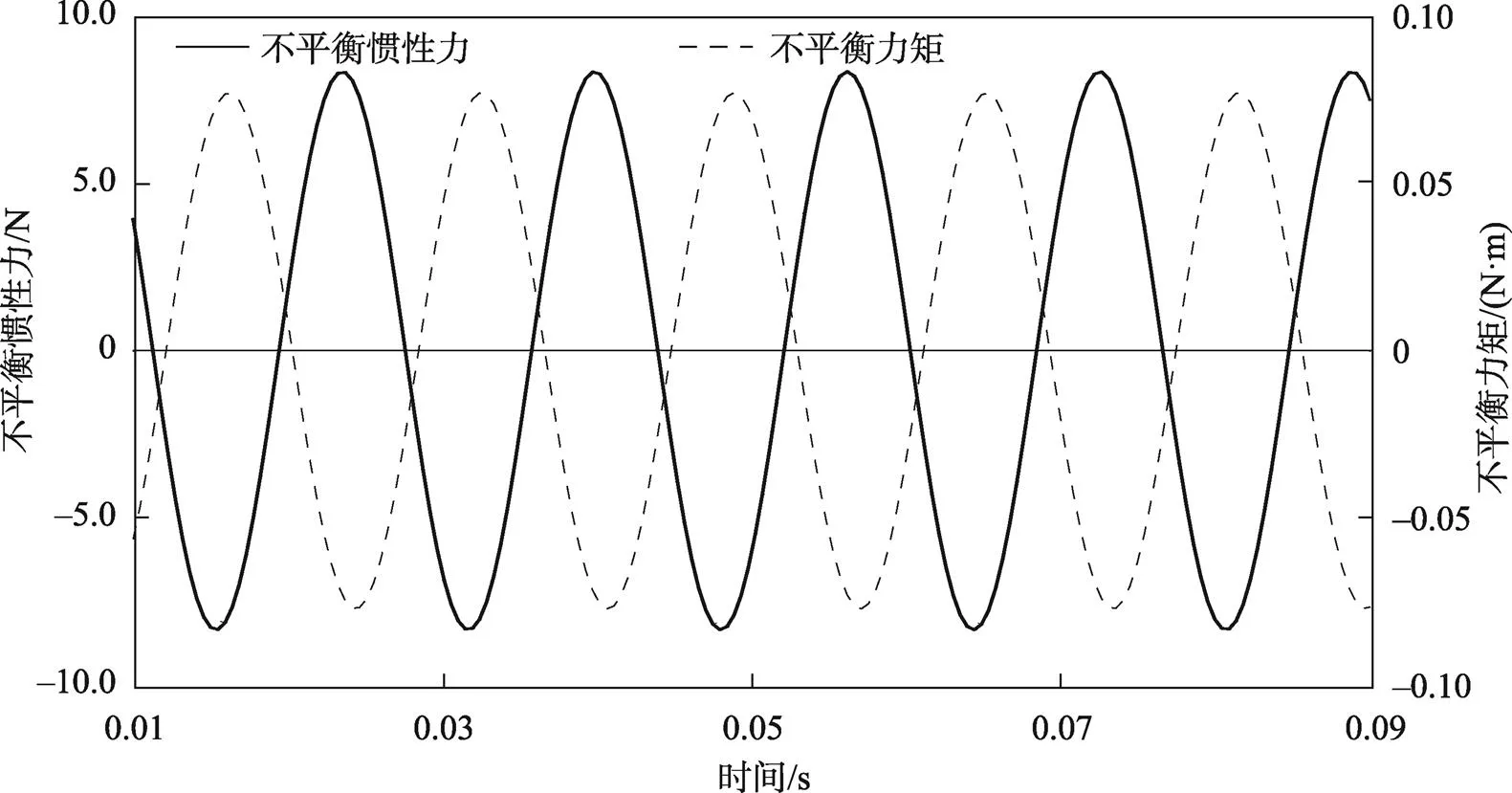
图4 曲轴惯性力及力矩曲线
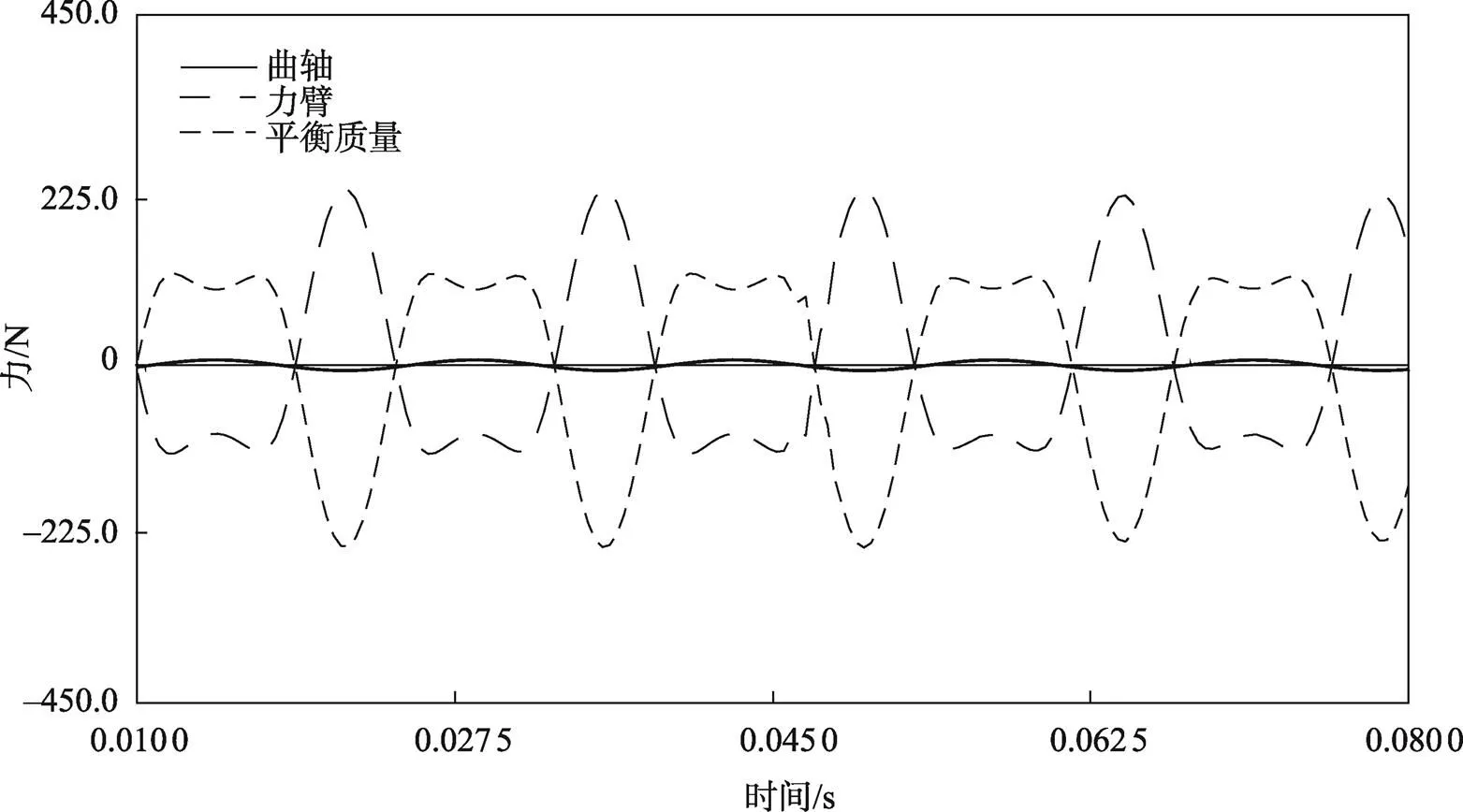
图5 平衡效果验证结果曲线
图5中整个机构平衡后剩余的往复惯性力极大值为7.564 2 N,极小值为6.777 3 N。剩余往复惯性力与刀臂、平衡质量及曲轴剩余往复惯性力之间的关系对应。往复锯平衡机构平衡了刀臂往复惯性力的96.65%的力。往复锯剩余的不平衡力主要由曲轴产生,其主要原因是没有考虑螺钉及螺钉安装孔对下半曲轴上凸台和上半曲轴的质量及其分布产生的影响。显然,往复锯剩余的往复惯性力数值较小。文中对刀臂和平衡质量的质心均进行了调整,受限于机构布置空间等因素,刀臂和平衡质量的质心未达到同一平面,其距离质心相差约6.06 mm,因为,整个机构存在未完全平衡的往复惯性力矩,其计算值为1.28 N·m,数值较小。
2 往复锯关键零部件有限元分析
竹材切割机械臂往复锯的核心机构材质均采用Q235,密度为7 850 kg/m3、弹性模量为210 Gpa、屈服强度为235 MPa、泊松比取0.3。文中Q235的许用应力值为210 MPa。由于往复锯核心机构为整个机械臂受力或应变最大的区域,因此,需要对核心机构零件及内壳体进行有限元分析,求得其最大主应力,并进行强度校核,确保往复锯核心机构零件满足强度要求。
2.1 关键力估算及仿真计算
由参考文献[15—16]可知,往复锯的锯切力受到锯齿数的影响最大,进给速度次之,锯的转速影响最小,且锯切力与锯切线速度成反比。参考文献[15]选择往复锯电机功率为0.62 kW,当往复锯转速为4 200 r/min时,其平均线速度为1.89 m/s;当圆锯转速为2 800 r/min时,其锯齿中点线速度为33.72 m/s,圆锯锯切力为12.09 N,因此,估计的往复锯平均锯切力为215.7 N。在Adams中测得,往复锯在转速为4 200 r/min时的锯切最大线速度为7.2 m/s。在锯切时,锯切线速度影响了单位时间内的切削齿数进而影响锯切力的大小,因此文献[15—16]近似认为往复锯锯片线速度与锯切力呈反比关系,且当锯切线速度达到最大值时的锯切力为0,因而估计的往复锯最大锯切力为291.92 N,取整数后即为300 N。Adams中上下曲轴受力曲线仿真结果[15-16]见图6,图6中受力分析均是往复锯在空载时的仿真结果。
图6中,上半曲轴与滑动轴承接触面受到的力在轴方向上的分力有极大值为239.54 N,此时对应轴方向上的分力为0.056 2 N;在轴方向上的分力有极小值为120.483 1 N,对应的轴方向上的分力有极大值为61.739 7 N。显然由于往复锯机构是等效的曲柄连杆机构,使得上半曲轴受到了刀臂施加的轴方向的力。上半曲轴与下半曲轴连接处的受力其极值为25.577 7 N。下半曲轴受到的上半曲轴施加的力矩的极值为3.852 N·m,当上半曲轴与滑动轴承接触面受力在轴方向分力取值为0时,传递的扭矩值为0.102 N·m。
2.2 刀臂有限元分析
刀臂虽然是运动件,但在Ansys软件中仍然可以将其作为静态结构进行有限元分析,其受力均取最大值。为使刀臂仿真结果更接近实际情况,在刀臂导入Ansys软件前,应在刀臂上添加虚拟凸台,位置在刀臂与滑动轴承的连接处,虚拟凸台与刀臂作为整体进行分析,为使得网格划分更准确,刀臂零件中,凸台、刀臂、前臂和焊接处应当分开进行网格划分,网格采用四面体网格。
刀臂上添加的受力主要包括加速度和前臂上的受力。考虑往复锯锯片也存在往复惯性力,因此刀臂添加的受力大小等于2.1节计算出的往复锯切削力的最大值加上锯片往复惯性力的最大值,锯片往复惯性力的最大值估算为刀臂往复惯性力的极大值。刀臂进行有限元分析后的应力云图见图7(其中虚拟凸台已隐藏),图7中最大主应力的极大值为37.672 MPa,远小于Q235许用应力210 MPa。
2.3 上半曲轴有限元分析
上半曲轴受到刀臂经滑动轴承传递的力、平衡质量经滑动轴承传递的力。将刀臂模型导入Ansys作为静态结构分析,为使网格划分效果更好,将上半曲轴上、下凸台及本体分开进行网格划分,且网格划分以四面体主导。由于上半曲轴下凸台的受力均传递至下半曲轴凸台上,为保障仿真结果与实际相符,文中在下凸台内连接凹槽内增加单独划分网格的虚拟凸台,并使虚拟凸台与上半曲轴模型一同进行有限元分析,其中,虚拟凸台与上半曲轴的下表面接触处,并保留0.1 mm间隙。仿真结果见图8。
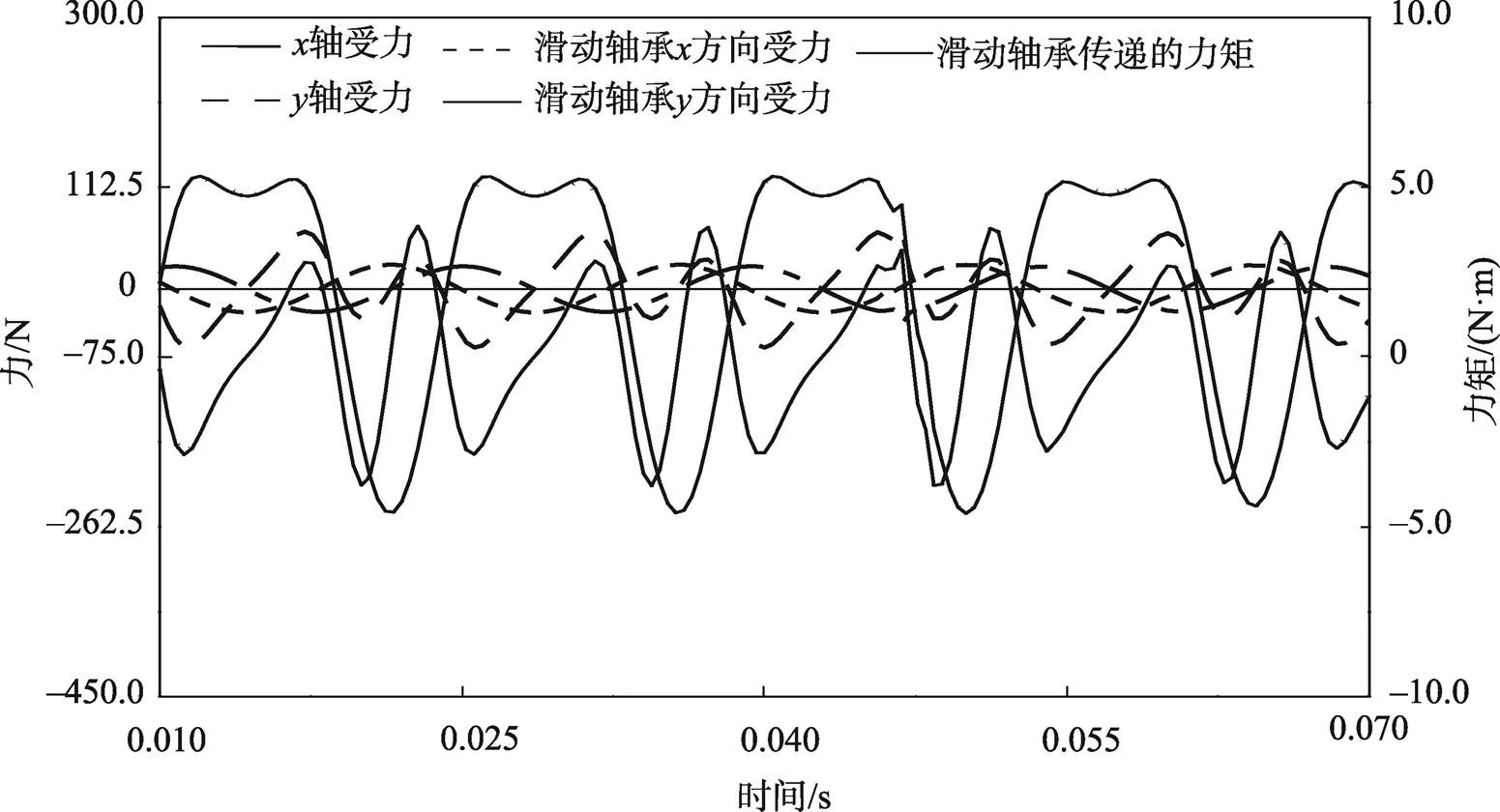
图6 曲轴受力曲线
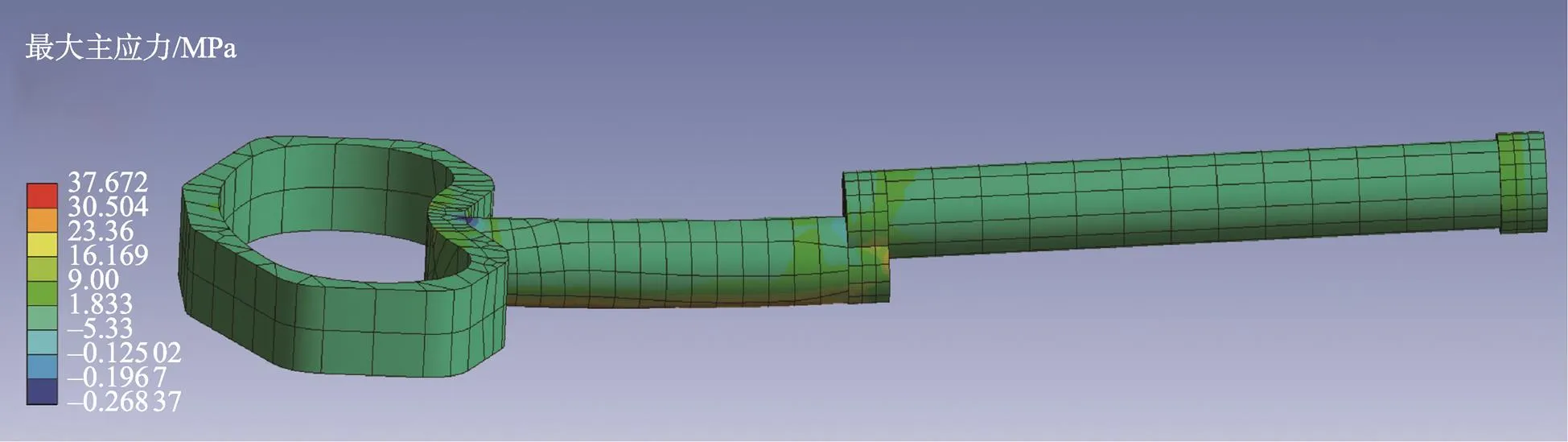
图7 刀臂应力云图
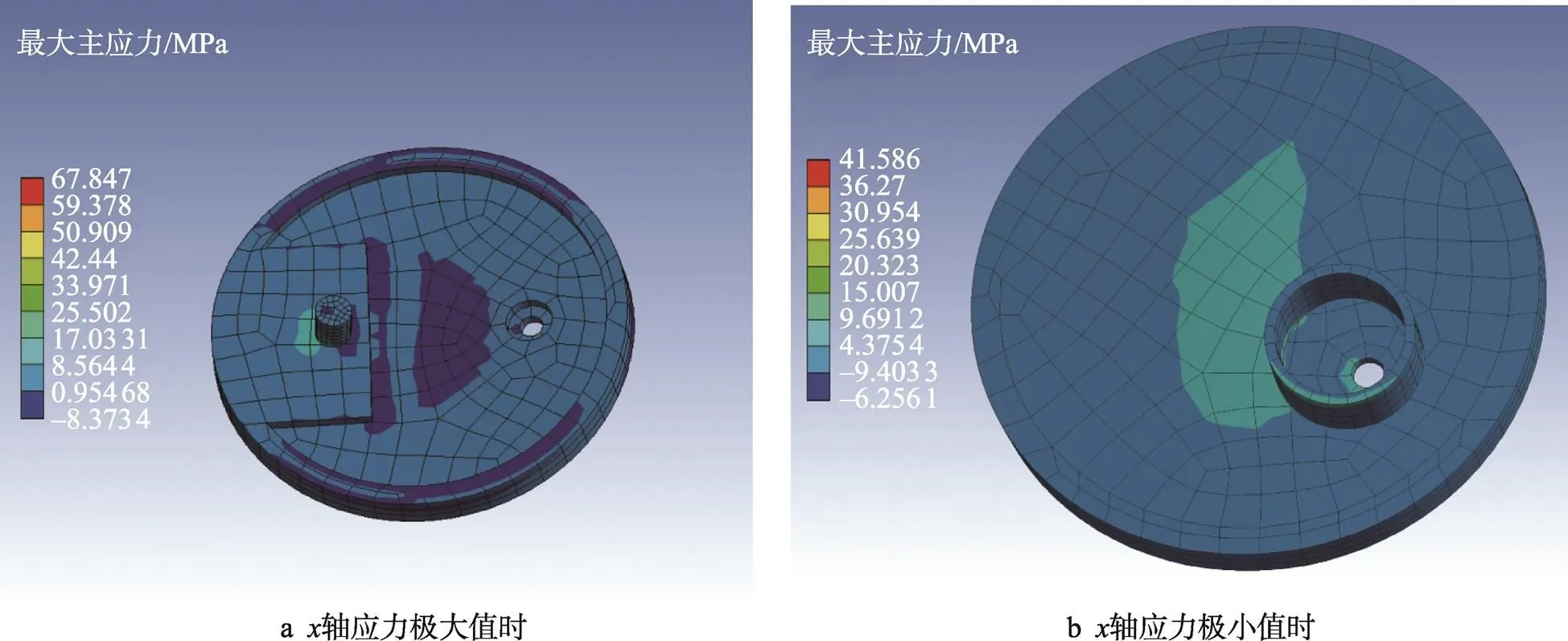
图8 上半曲轴应力云图
在进行有限元分析时,上半曲轴材质选择Q235,上半曲轴受力主要有刀臂施加的力、平衡质量的惯性力和上半曲轴自身旋转的惯性力。其中,刀臂施加的力包括刀臂、锯片的惯性力和切削力。由图6可知,往复锯空载时,上半曲轴受到的刀臂惯性力呈周期性变化,由于往复锯机构等效为曲柄连杆机构,因而上半曲轴在轴方向受力到达极小值时,其在轴方向受力同时到达极值,因此,有限元分析时上半曲轴分别在受力取得极大值及极小值时进行有限元分析,且当上半曲轴在轴受力取得极小值时,近似认为此时的锯切力等于最大锯切力。
图8a是上半曲轴在轴受力到达极大值时的应力云图,图8b是上半曲轴在轴受力到达极小值时的应力云图(其中虚拟凸台已隐藏)。由上半曲轴的有限元分析可知,上半曲轴最大主应力的最大值为67.847 MPa,远小于Q235的许用应力210 MPa,且上半曲轴上凸台为薄弱环节。从图8b中可看到,上半曲轴螺钉孔实现了曲轴间力矩的传递作用。
2.4 下半曲轴有限元分析
下半曲轴,主要受力是自身的旋转惯性力及上半曲轴施加的力。由于Adams是将物体作为刚体进行受力分析,因此如图6所示,在往复锯空载时,上半曲轴施加给下半曲轴的力在轴是周期性的正弦力,在轴是周期性余弦力,力的极值为25.577 7 N。上半曲轴施加的力近似认为是上半曲轴旋转的惯性力引起的。显然,下半曲轴凸台与上半曲轴凸台配合在一起,共同参与受力形变,因此直接采用Adams仿真结果作为下半曲轴受力分析结果与实际情况不相符合。
在进行有限元分析时,应当在上半曲轴模型上添加虚拟凸台,其形状与上半曲轴接触处相同,且下半曲轴凸台与上半曲轴下表面接触处时应留有空隙,下半曲轴与上半曲轴应保留螺钉的配合关系,虚拟凸台与下半曲轴应一同进行有限元分析,网格划分的方法是将下半曲轴分为8段,并与虚拟凸台一起分别进行六面体网格划分。在有限元分析时,将刀臂施加的力的作用点设置在虚拟凸台上更符合实际情况。模型主要受力有虚拟凸台受到的平衡质量惯性力、上半曲轴旋转的惯性力、刀臂传递的刀臂和锯片惯性力以及最大切削力。参考上半曲轴有限元分析,下半曲轴分析也分为当刀臂与滑动轴承接触面受力取得极大值和极小值时的2种情况。
当下半曲轴在刀臂与滑动轴承接触面受力取得极大值和极小值时的有限元分析应力云图(虚拟凸台已隐藏)见图9a—b,测得的主应力极大值为70.645 MPa,远小于Q235的许用应力值210 MPa。下半曲轴的薄弱环节是凸台与曲柄比的连接处。
2.5 往复锯内壳体有限元分析
SolidWorks中建立的往复锯内壳体模型见图10。内壳体左中位置凹槽装配有深沟球轴承,并将往复锯曲轴的力传递给内壳体。内壳体结构过于复杂,因而直接对内壳体进行有限元分析,网格划分复杂,且过于消耗计算资源。考虑到内壳体主要受力点在其左中凹槽处,离主要受力点较远处应变一般较小,因而,应当对内壳体进行简化处理后再进行有限元分析。
内壳体简化模型网格划分方法以六面体主导,其受力主要有滑动轴承施加的水平方向力及力矩,力的大小为曲轴不平衡力与切削力最大值之和,其大小取310 N,力矩为往复锯不平衡力矩与切削力对内壳体受力点力矩之和,内壳体所受力作用于面,因此取受力面上最远处作为计算力矩的作用点,力矩数值为7.6 N·m。为使得有限元分析更靠近真实情况,在内壳体配合轴承处添加虚拟空心壳体作为力的传递中介,并与外壳体一同进行有限元分析,空心壳体壁厚为深沟球轴承的壁厚,其数值为4 mm。
壳体简化模型正面及背面的应力云图见图11a—b(其中虚拟凸台已隐藏),其最大主应力数值的最大值为34.026 MPa,远小于Q235的许用应力值201 MPa。
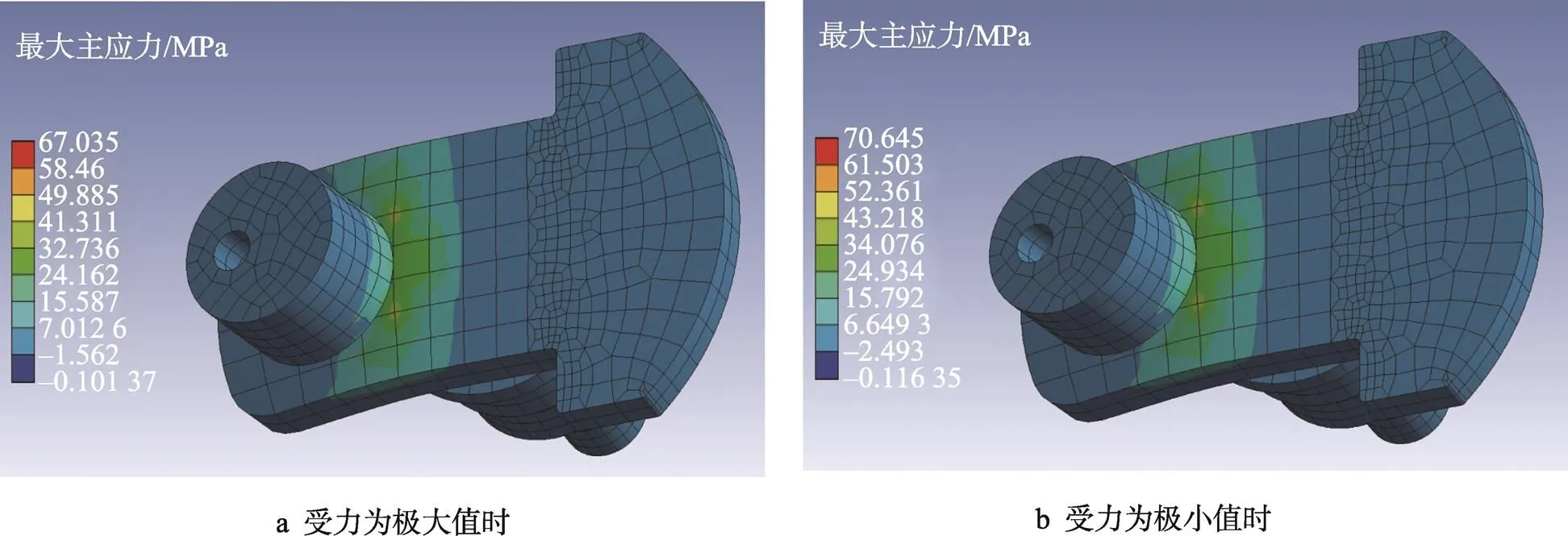
图9 下半曲轴受力应力云图

图10 往复锯内壳体模型
3 竹材切割机械臂模型
3.1 相关零部件选型
为便于竹材切割机械臂往复锯在供电及在停电状态下工作,采用24 V永磁无刷电机进行驱动,并使用24 V转换电源或锂离子电池电源供电,电机与往复锯曲轴间采用带惰轮的斜齿轮变速器传动,其中,主动齿轮齿数选择47齿,惰轮选择23齿,从动齿轮选择41齿;主动齿轮与惰轮、从动齿轮与惰轮齿数分别互质。
主材切割机械臂其他外购件包含无刷电机、步进电机、直线轴承及光杆、滚珠丝杠、深沟球轴承等。各零件在机械臂中的应用见第3.3节。
3.2 竹材切割机械臂模型
在SolidWorks中建立的竹材切割机械臂模型见图12。图12a为机械臂整体结构,图12b为往复锯模型。其中,往复锯机支架与导轨盒之间由光轴和直线轴承连接,横向移动由步进电机带动滚珠丝杠实现。往复锯由双曲柄滑块机构、齿轮机构、内壳体、永磁无刷电机、散热风扇和外壳体等组成。
竹材切割机械臂的工作原理:夹具固定竹材后,永磁无刷电机经变速器带动往复锯工作,使得锯片往复运动,同时步进电机驱动滚珠丝杠,使得往复锯做横向进给运动,从而完成竹材切割。
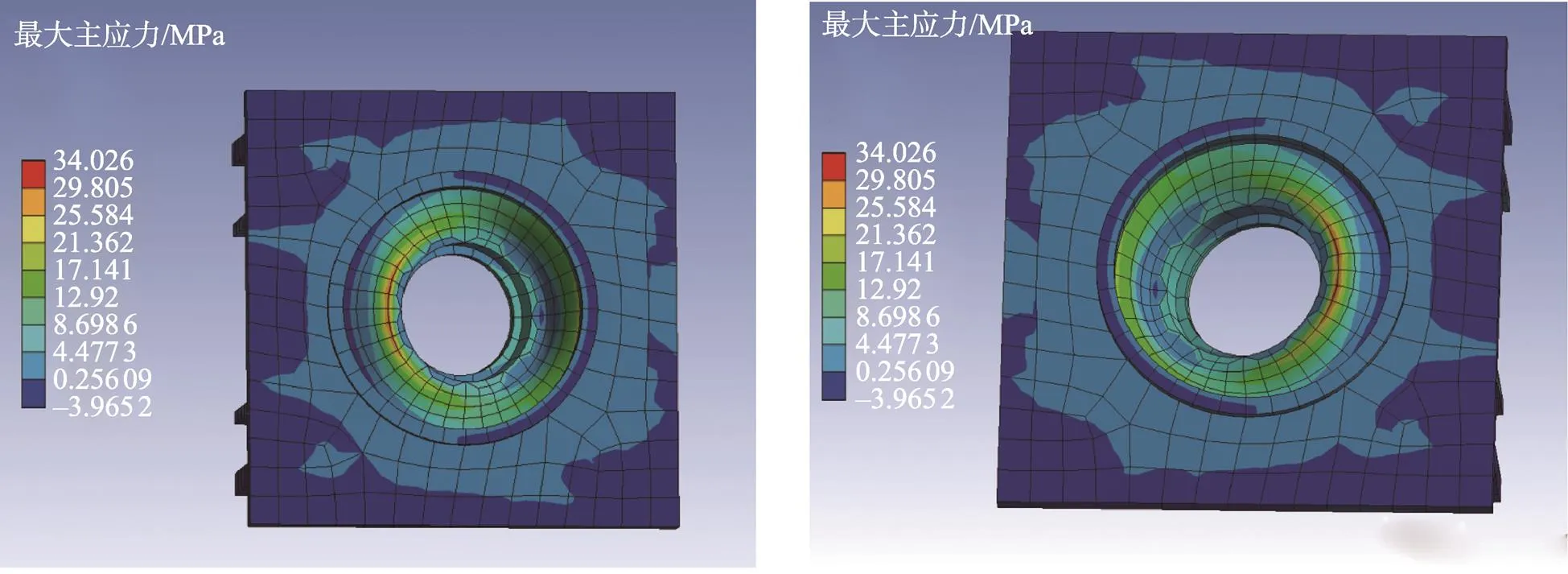
图11 壳体简化模型应力云图
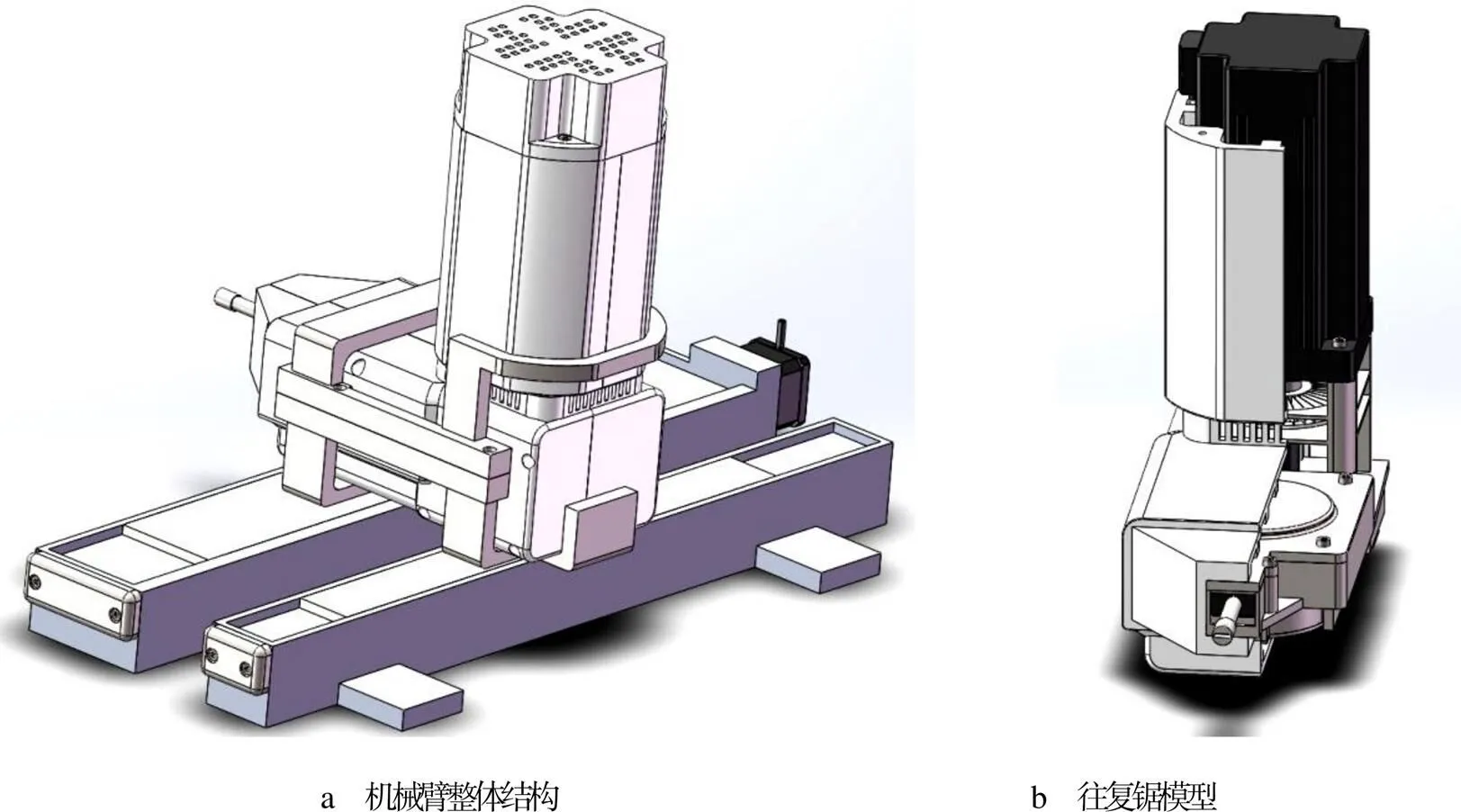
图12 竹材切割机械臂模型
3.3 竹材切割机械臂工程图及分析
竹材切割机械臂及往复锯的工程图见图13a—b。分析机械臂运动可得,机械臂主要运动为往复锯做横向进给运动,同时往复锯锯片做往复运动,因而竹材切割机械臂有2个自由度,需要2个原动件协同驱动,以实现竹材切割功能。
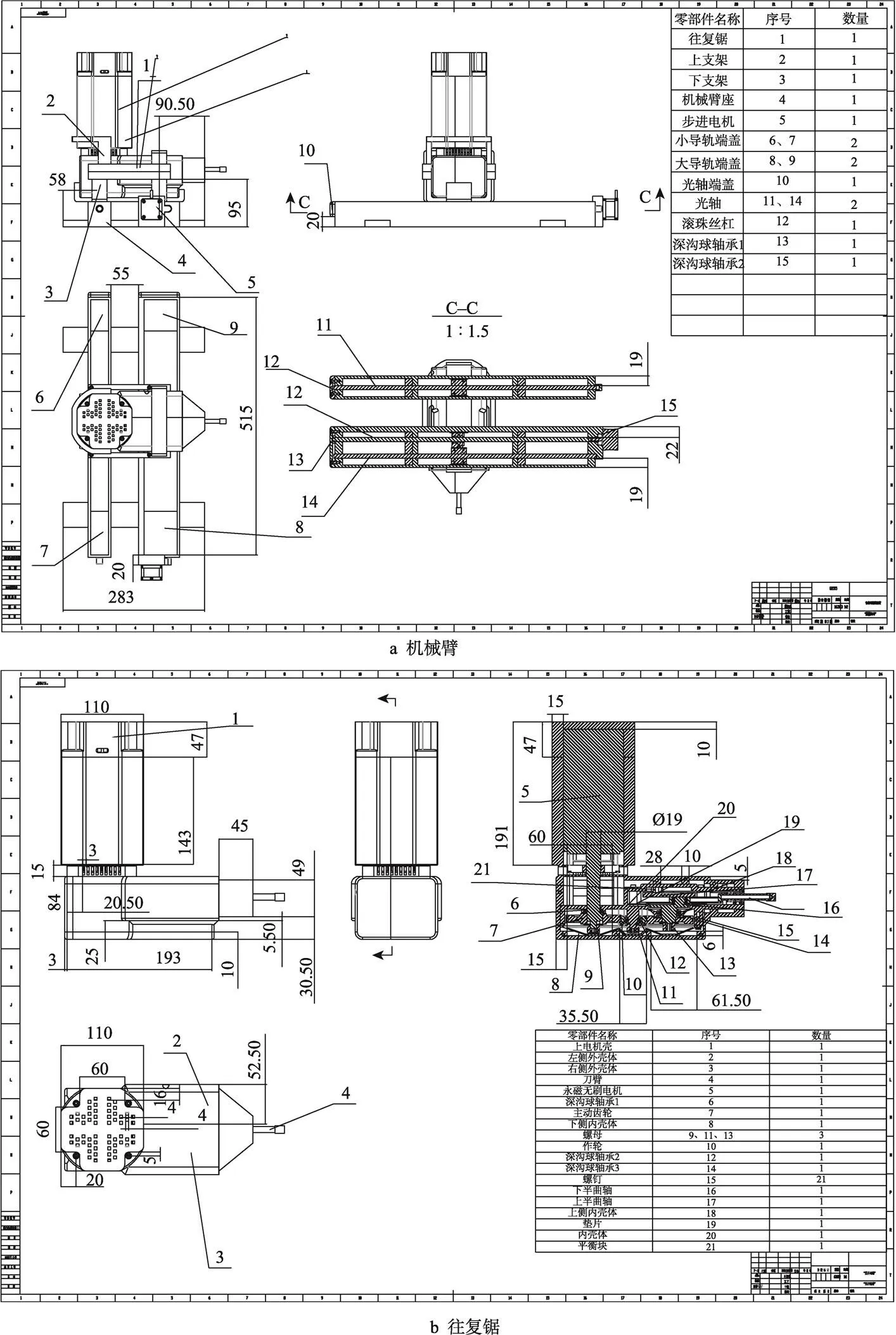
图13 竹材切割机械臂工程图
4 结语
文中设计了一种竹材切割机械臂,其原理是通过永磁无刷电机经斜齿轮变速器带动往复锯实现锯切运动,用过步进电机带动滚珠丝杠实现机械臂的切削的进给运动。针对往复锯存在的往复惯性力,设计了平衡机构,经Adams仿真验证了其平衡效果较好。对刀臂、上半曲轴、下半曲轴等往复锯核心机构零件及内壳体进行了有限元分析,并求得了其最大主应力极值。经验证,刀臂、上半曲轴、下半曲轴及内壳体最大主应力极大值均远小于Q235许用应力值,因此往复锯核心机构零件及内壳体均满足强度条件。
由于布置空间及成本的考虑,该平衡机构剩余1.28 N的不平衡力矩未平衡,但其数值较小,后期可对此进行进一步改进。
[1] 胡甫才, 魏志威, 徐阳. 基于理论分析与仿真验证的船用空压机平衡轴设计[J]. 武汉理工大学学报(交通科学与工程版), 2018(6): 937-941.
HU Fu-cai, WEI Zhi-wei, XU Yang. Design of Balanced Shaft of Marine Air Compressor Based on Theoretical Analysis and Simulation Verification[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2018(6): 937-941.
[2] CHEN Yu, WU K, WU X. Kinematic Accuracy and Nonlinear Dynamics of a Flexible Slider-Crank Mechanism with Multiple Clearance Joints[J]. European Journal of Mechanics - A/Solids, 2021, 88: 104277.
[3] BECKERS Jarl. Analysis of the Dynamics of a Slider-Crank Mechanism Locally Actuated with an Act-And-Wait Controller[J]. Mechanism and Machine Theory, 2021, 159: 104253.
[4] 蔡吉洲. 内燃机使用往复运动与旋转运动转换机构分析[J]. 内燃机与配件, 2021(9): 50-51.
CAI Ji-zhou. Analysis of Using Reciprocating Motion and Rotary Motion Conversion Mechanism of Internal Combustion Engine[J]. Internal Combustion Engine & Parts, 2021(9): 50-51.
[5] ALBAGHDADI A M, BAHAROM M B, SULAIMAN S A. Parameter Design Optimization of the Crank-Rocker Engine Using the FMINCON Function in MATLAB[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1088(1) : 012072.
[6] 黄磊, 宋秀英, 李云霄, 等. 基于ADAMS四缸发动机的平衡轴仿真分析[J]. 内燃机与配件, 2017(9): 29-31.
HUANG Lei, SONG Xiu-ying, LI Yun-xiao, et al. The ADAMS Simulation Analysis of Four-Cylinder Engine Balance Shaft[J]. Internal Combustion Engine & Parts, 2017(9): 29-31.
[7] 蒋义, 贾学宏, 李连豹, 等. 发动机曲柄连杆机构平衡性分析及平衡轴设计[J]. 小型内燃机与车辆技术, 2019(6): 33-37.
JIANG Yi, JIA Xue-hong, LI Lian-bao, et al. Balance Analysis and Balance Shaft Design of Crank-Connecting Rod Mechanism of Engine[J]. Small Internal Combustion Engine and Vehicle Technique, 2019(6): 33-37.
[8] SAMIKSHA A, VIKAS B. Optical Dynamic Balancing of Shaking Force and Shaking Moment for Planar Mechanisms[J]. Int. J. of Intelligent Machines and Robotics, 2018, 1(2): 109-121.
[9] ETESAMI G, FELEZI M E, NARIMAN Z N. Optimal Transmission Angle and Dynamic Balancing of Slider-Crank Mechanism with Joint Clearance Using Pareto Bi-Objective Genetic Algorithm[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(4).
[10] VECIANA F J, JORDI N, LORES G E. Residual Vibration Reduction in Back-And-Forth Moving Systems Driven by slider-Crank Mechanisms Working Through a Dead Point Configuration[J]. Mechanism and Machine Theory, 2021, 158(4): 104239.
[11] 李婷婷, 张振山, 崔国华, 等. 含间隙铰曲柄滑块机构中接触力计算方法对比研究[J]. 机械传动, 2021, 42(2): 39-47.
LI Ting-ting, ZHANG Zhen-shan, CUI Guo-hua, et al. Comparative Study on Calculation Method of Contact Force in Joint with Clearance of Crank Slider Mechanism[J]. Journal of Mechanical Transmission, 2021, 42(2): 39-47.
[12] DANG Hoang Minh. Development of a Generalized Mathematical Model for Slider-Crank Mechanism Based on Multiobjective Concurrent Engineering with Application[J]. Arabian Journal for Science and Engineering, 2021, 1: 1-17.
[13] ZHANG Sui Motion Simulation Design of Crank-Connecting Rod Mechanism of Automobile Engine[J]. Journal of Physics: Conference Series, 2021, 1798(1): 012040.
[14] WU Xuze et al. Correlation dimension and bifurcation analysis for the planar slider-crank mechanism with multiple clearance joints[J]. Multibody System Dynamics, 2021: 1-22.
[15] 欧阳丛森, 朱振杰, 张进生. 锯切花岗岩过程中金刚石框架锯的锯切力研究[J]. 工具技术, 2021, 55(9): 36-41.
OUYANG Cong-sen, ZHU Zhen-jie, ZHANG Jin-sheng. Research on Sawing Force of Diamond Frame Saw in Process of Sawing Granite[J]. Tool Engineering, 2021, 55(9): 36-41.
[16] 杨春梅, 张振宇, 马岩. 自走式轻型竹材采伐机的设计与分析[J]. 林产工业, 2019, 46(6): 23-28.
YANG Chun-mei, ZHANG Zhen-yu, MA Yan. Design and Analysis of Self-Propelled Light Type Bamboo Cutting Machine[J]. China Forest Products Industry, 2019, 46(6): 23-28.
Design and Simulation of Bamboo Cutting Manipulator and Parts
WANG Hui, CUI Sheng-le, AN Yang, YANG Chun-mei
(Northeast Forestry University, Harbin 150040, China)
In view of the need to cut bamboo in the manufacture of bamboo wood-based panel for packaging, the work aims to design a bamboo cutting manipulator driven by brushless motor and a balance mechanism of reciprocating to balance the reciprocating inertia force. The strength of the core mechanism parts and inner shell of the reciprocating saw were checked to ensure that the weak links of the parts meet the strength requirements. The reciprocating saw mechanism and its balance mechanism were established in Solidworks, and the balance effect of the balance mechanism was verified through Adams simulation. In Ansys software, finite element analysis was performed on the core parts of the reciprocating saw and its balance mechanism, and the maximum principal stress was obtained for strength check. Finally, the main material cutting manipulator was designed and completed. Adams simulation showed that the maximum remaining reciprocating inertial force of the reciprocating saw was 7.564 2 N, and the balance ratio was 96.65%. Ansys finite element analysis showed that the maximum value of the maximum principal stress of each part was 70.645 MPa, which was far less than 210 MPa, the allowable stress value of Q235. The reciprocating saw in the bamboo cutting robot arm designed in this article has a small residual reciprocating inertia force after being balanced by the balance mechanism. Its core mechanism parts and inner housing meet the strength requirements, and the design of main material cutting manipulator meets the requirements.
manipulator; crank connecting rod mechanism; reciprocating inertia force; strength check
TH122
A
1001-3563(2022)17-0165-09
10.19554/j.cnki.1001-3563.2022.17.021
2021–11–18
广东省重大专项研发计划项目(2020B020216001);中央高校基本科研业务费专项资金项目资助(2572020DR12)
王慧(1965—),女,副教授,主要研究方向为林业与木工机械。
责任编辑:曾钰婵

