基于模糊PID的包装覆膜自适应恒张力控制方法

王志广，郭亚东

基于模糊PID的包装覆膜自适应恒张力控制方法

王志广1，郭亚东2

（1.开封技师学院，河南 开封 475004；2.南阳技师学院，河南 南阳 473001）

为提高极限条件下对包装覆膜自适应恒张力的控制效果，基于模糊PID设计了一种新的控制方法。首先通过参数拟合分析建立了包装覆膜的结构力学分析模型，并采用荷载-挠度全曲线拟合方法模拟了包装覆膜力学参数，然后结合区域–合并连续估计方法得到结构参数解析模型。在此基础上，通过外荷载作用力学评估分析，在极限转动刚度作用下，构建了弹塑性力学模型。然后通过极限抗力分析和屈服应力学参数的优化评估，得到抗弯刚度软化模型，继而基于模糊PID控制实现包装覆膜的自适应控制优化。应用该方法后，包装覆膜自适应恒张力的输出稳定性较强，参数寻优能力较好。根据实验结果可知，上述恒张力控制方法具有较好的控制效果。

模糊PID；包装覆膜；恒张力控制；力学模型；参数辨识；极限抗力

目前，包装覆膜被广泛应用于现代包装结构中，其在美化包装和提高包装的安全性方面具有较优越的性能。在包装覆膜的设计和应用中，需对其自适应恒张力展开控制[1]。根据包装覆膜组成的特殊性，需要对包装覆膜的基础结构进行优化分析，即根据包装覆膜自适应恒张力特征分析其力学变化情况，然后结合量化分析和参数寻优方法控制包装覆膜自适应恒张力[2-3]。

有效的张力控制能够提高包装覆膜的质量，因此，相关的包装覆膜自适应恒张力控制方法研究受到人们的极大关注。目前，应用较为广泛的控制方法有基于模糊非线性积分的张力控制方法[4]、基于神经网络PID的张力控制方法[5]等，但传统方法的控制过程对覆膜自适应恒张力控制性能分析和评估的效果不理想，导致其输出的自适应张力稳定性较低。

针对传统方法中存在的问题，文中基于模糊PID设计一种新的包装覆膜自适应恒张力控制方法。首先构建模糊PID控制下的包装覆膜的恒张力学特征响应模型，然后建立矩形板作为包装覆膜的叠层结构构件模型，通过外荷载作用力学评估分析构建正截面抗弯的弹塑性力学模型，通过极限抗力分析和屈服应力学参数的优化估计，实现对包装覆膜自适应恒张力控制性能评估和参数优化估计；再采用模糊PID控制技术实现参数寻优和模糊特征融合解析控制；最后进行仿真测试分析，验证本方法在包装覆膜自适应恒张力控制方面的优越性。

1 包装覆膜叠层结构力学分析和参数解析

1.1 包装覆膜叠层结构力学分析

通过建立模糊PID控制下的包装覆膜自适应恒张力控制模型，再对张力控制参数拟合过程展开分析，能够有效提高包装覆膜模糊PID控制稳定性。为此，通过分析包装覆膜叠层结构融合特征建立其结构力学分析模型，再通过刚度模拟和有限元分析技术[6-7]，分析模糊PID控制对包装覆膜力学参数的结构特征的影响，得到在弯曲承载力作用下附加承载力融合模型：

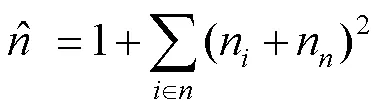
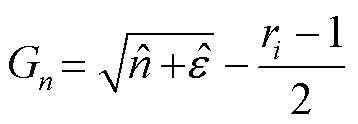
其中：

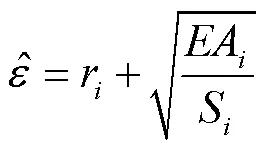
在此基础上，采用包装覆膜的极限承载力特征分析方法，得到包装覆膜叠层结构的空间载荷分布集：

通过数值模拟和增量系数融合，在常态化空间载荷扰动下，得到包装覆膜模糊PID控制的载荷特征分析模型：

根据上述分析，在类噪声小波分解[8-9]的基础上，得到包装覆膜叠层结构的力学分析模型：

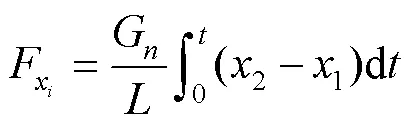
1.2 包装覆膜叠层结构参数解析

在分析包装覆膜叠层结构力学变化的基础上，采用荷载−挠度全曲线拟合方法模拟包装覆膜力学参数，并对力学参数展开分析，从而结合参数拟合实现力学评估优化。首先根据包装覆膜叠层结构得到其结构关系式：

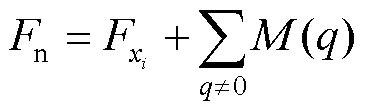
式中：为拉伸长度；为承载力的增量系数。

根据上述分析，在等效惯量的侧向移动下，采用荷载-挠度全曲线拟合方法对力学参数展开拟合处理，得到包装覆膜叠层结构的参数拟合方程，其表达如下：

其中：

在此基础上，通过区域–合并连续估计方法，并通过模糊PID控制过程对包装覆膜自适应恒张力控制性能参数展开评估[11-12]，从而得到包装覆膜叠层结构参数解析模型：

综上分析，构建了包装覆膜叠层结构参数解析模型，基于此，可根据力学参数解析结果对包装覆膜叠层结构的自适应恒张力控制性能展开分析。

2 自适应恒张力控制性能优化评估

2.1 外荷载作用力学评估

通过外荷载作用力学评估分析，可构建正截面抗弯的弹塑性力学模型，从而进行极限抗力分析和屈服应力学参数下的优化估计，由此可得到包装覆膜叠层结构的外载荷，其表达如下：

其中：

在外荷载作用下，包装覆膜会受到正弯矩作用影响产生形变。为此，建立包装覆膜叠层结构试验板的荷载−变形耦合式：

在上述分析的基础上，计算外荷载作用力学评估函数，其过程如下：

通过弹塑性力学模型进行包装覆膜的外荷载作用力学评估，从而提高对包装覆膜叠层结构的自适应覆膜控制能力，通过上述模型的离散化处理，再利用模糊PID控制算法对包装覆膜的外载荷进行优化。

2.2 基于模糊PID控制的包装覆膜自适应控制优化

在不同扰动幅值下，结合上述得到的外荷载作用力学评估结果，对包装覆膜模糊PID控制的模糊参数展开科学、合理估计，合理考虑向塑性阶段过渡的过程，得到包装覆膜模糊PID控制的应力关系应满足：

结合外荷载的影响，得到包装覆膜模糊PID控制的应变预测输出为：

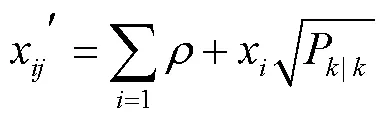
3 性能试验与测试结果分析

为验证基于模糊PID的包装覆膜自适应恒张力控制方法的实际应用性能，通过试件加载的方法进行测试。

实验选取7块不同规格型号的包装覆膜作为测试试件，对其包装过程自适应恒张力展开控制，试件屈服载荷的范围控制在34～60 kPa，最小极限承载力为20 kN，最大极限承载力为600 kN。测试试件参数见表1。

表1 包装覆膜模糊PID控制参数分析

Tab.1Analysis of fuzzy PID control parameters of packaging film

根据表1中设定的参数进行包装覆膜模糊PID控制。首先对不同厚度包装覆膜叠层结构进行有限元分析，得到的结果见图1。

图1 不同厚度包装覆膜叠层应力分析结果

由图1可知，包装覆膜叠层结构的自适应恒张力的变化情况规律性不明显，因此，分别利用文中设计的基于模糊PID的方法和传统的基于模糊非线性积分的张力控制方法、基于神经网络PID的张力控制方法，对包装覆膜自适应恒张力展开控制（结果以试件1和4为例），得到的结果见图2。

分析图2可以发现，随着试件挠度的逐渐增加，不同控制方法下包装覆膜的自适应恒张力也在不断发生变化。理论情况下，覆膜的自适应恒张力应呈现先增加后减小的趋势。文中所提方法的控制曲线呈现这种趋势，且与理论曲线重叠度最高。2种传统方法控制下的薄膜张力变化情况不稳定，且与理论曲线之间存在一定差距。综上所述，基于模糊PID的方法能够有效实现对包装覆膜自适应恒张力的控制。

图2 包装覆膜自适应恒张力控制性能分析

4 结语

提出了一种基于模糊PID的包装覆膜自适应恒张力控制方法，通过力学参数优化分析方法构建了包装覆膜模糊PID控制的荷载特征分析模型，提高了包装覆膜模糊PID控制的稳定性。经实验分析可知，该方法对包装覆膜自适应恒张力控制的效果较好。在接下来的研究中，将考虑从控制时效性方面进一步提高该方法的应用性能。

[1] 李坤全, 文睿. 瓦楞纸板生产线原纸张力自适应模糊PID控制[J]. 包装工程, 2017, 38(7): 135-138.

LI Kun-quan, WEN Rui. Adaptive Fuzzy PID Control of Base Paper Tension in Production Line for Corrugated Board [J]. Packaging Engineering, 2017, 38(7): 135-138.

[2] 秦国防, 秦明辉. 包装覆膜自适应恒张力控制方法研究[J]. 包装工程, 2020, 41(15): 222-226.

QIN Guo-fang, QIN Ming-hui. Research on Adaptive Constant Tension Control Method of Packaging Film[J]. Packaging Engineering, 2020, 41(15): 222-226.

[3] 高雅, 朱秦岭, 宋晓茹. 绕线系统的模糊PID与矢量控制方法研究[J]. 控制工程, 2018, 25(6): 1134-1138.

GAO Ya, ZHU Qin-ling, SONG Xiao-ru. Research on Control Strategy of Fuzzy PID Winding System[J]. Control Engineering of China, 2018, 25(6): 1134-1138.

[4] 陈星旭, 胡明, 马维东. 模糊非线性积分滑模张力控制系统的研究[J]. 组合机床与自动化加工技术, 2020(3): 103-105.

CHEN Xing-xu, HU Ming, MA Wei-dong. Research on Fuzzy Nonlinear Integral Sliding Mode Tension Control System[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(3): 103-105.

[5] 雷莹. 吹膜机塑料薄膜张力的自适应神经网络PID控制[J]. 合成树脂及塑料, 2019, 36(3): 72-75.

LEI Ying. Adaptive Neural Network Pid Control for Plastic Film Tension of Film Blowing Machine[J]. China Synthetic Resin and Plastics, 2019, 36(3): 72-75.

[6] 孙广志, 张桂香, 陈春增, 等. 覆膜角度对运动薄膜非线性振动的影响[J]. 机械科学与技术, 2020, 39(5): 662-667.

SUN Guang-zhi, ZHANG Gui-xiang, CHEN Chun-zeng, et al. Effect of Different Film Angle on Nonlinear Vibration of Moving Films[J]. Mechanical Science and Technology for Aerospace Engineering, 2020, 39(5): 662-667.

[7] PRIEZJEV N V. Slow Relaxation Dynamics in Binary Glasses during Stress-Controlled, Tension-Compression Cyclic Loading[J]. Computational Materials Science, 2018, 153: 235-240.

[8] YAN F, Fan K, Yan X, et al. Constant Tension Control of Hybrid Active-Passive Heave Compensator Based on Adaptive Integral Sliding Mode Method[J]. IEEE Access, 2020, 4(17): 12-21.

[9] ZHI C, Guo J Z, Hong Z Y. A High-Precision Constant Wire Tension Control System for Improving Workpiece Surface Quality and Geometric Accuracy in WEDM[J]. Precision Engineering, 2018, 40(1): 7-13.

[10] 郑刚, 李斌, 梁于州. 模糊自适应PID控制的恒张力收卷系统研究[J]. 现代电子技术, 2017, 40(21): 132-135.

ZHENG Gang, LI Bin, LIANG Yu-zhou. Research on Constant Tension Winding System Based on Fuzzy Self-Adaptive PID Control[J]. Modern Electronics Technique, 2017, 40(21): 132-135.

[11] LU J S , Cheng M Y, Su K H, et al. Wire Tension Control of An Automatic Motor Winding Machine-An Iterative Learning Sliding Mode Control Approach[J].Robotics and Computer-Integrated Manufacturing, 2018, 50(4): 50-62.

[12] 汤伟, 王古月, 王露露. 新型悬浮包装中薄膜张力的模糊自适应PID控制[J]. 包装工程, 2018, 39(3): 141-145.

TANG Wei, WANG Gu-yue, WANG Lu-lu. Fuzzy Adaptive PID Control of Film Tension in New Suspension Package[J]. Packaging Engineering, 2018, 39(3): 141-145.

[13] CHEN Z, Zhang G J, Yan H Z. A high-Precision Constant Wire Tension Control System for Improving Workpiece Surface Quality and Geometric Accuracy in WEDM[J]. Precision Engineering, 2018, 27(5): 96-105.

[14] NANAKO M, Akira S. Active Vibration Control of Compensation Rope by Tension Based on Elevator Car Position and Acceleration During Operation of an Elevator in a Vibrating Building[J]. Transactions of the JSME (in Japanese), 2018, 43(9): 10-18.

[15] 朱耀麟, 周晓东, 武桐, 等. 模糊神经网络的长丝恒张力控制系统设计[J]. 单片机与嵌入式系统应用, 2019, 19(12): 72-75.

ZHU Yao-lin, ZHOU Xiao-dong, WU Tong, et al. Design of Filament Constant Tension Control System Based on Fuzzy Neural Network[J]. Microcontrollers & Embedded Systems, 2019, 19(12):72-75.

An Adaptive Constant Tension Control Method Based on Fuzzy PID for Packaging Film

WANG Zhi-Guang1, GUO Ya-Dong2

(1. Kaifeng Technician College, Henan Kaifeng 475004, China; 2. Nanyang Technician College, Henan Nanyang 473001, China)

The work aims to design a new control method based on fuzzy PID to improve the control effect of self-adaptive constant tension under the limit condition. Firstly, the structural mechanical analysis model of the packaging film was established by parameter fitting analysis. The mechanical parameters of the packaging film were simulated by load-deflection curve fitting method. And then the analytical model of the structural parameters was obtained by combining the area-combined continuous estimation method. On this basis, the elastoplastic mechanical model was constructed under the action of ultimate rotational stiffness through mechanical evaluation and analysis of external loads. Then the bending stiffness softening model was obtained after the ultimate resistance analysis and the optimal evaluation of the yield mechanical parameters, and then the adaptive control optimization was realized based on the fuzzy PID control. The simulation results showed that the output stability of the self-adaptive constant tension was stronger and the parameter optimization ability was good. According to the experimental results, the above constant tension control method has good control effect.

fuzzy PID; packaging film; constant tension control; mechanical model; parameter identification; extreme resistance

TB487

A

1001-3563(2022)17-0203-05

10.19554/j.cnki.1001-3563.2022.17.026

2022−05−21

王志广（1972—），男，高级讲师，主要研究方向为机械制造等。

责任编辑：曾钰婵