基于粒子群算法的桥式起重机模糊PID防摇控制
卜凡舟,孙玉国,卢凤娇
(上海理工大学光电信息与计算机工程学院,上海200093)
0 引 言
起重机在起吊和运载货物过程中会受到风载荷和机械惯性的影响,绳索悬挂吊重会产生近似无阻尼的振荡,仅靠空气阻尼自然消摆会花费大量时间,影响工作效率。此外,吊重摆动时产生的周期性力矩会对起重机结构造成疲劳损伤。因此,对起重机防摇控制进行研究具有重要的工程意义。目前,已有学者将智能控制算法(如最优控制、输入整型控制和粒子群算法)应用到桥式起重机防摇控制系统中。粒子群优化(Particle Swarm Optimization,PSO)算法因具有结构简单、调整参数少等优点而广泛应用于控制算法的参数优化中。PSO最早由KENNEDY等提出,其基本思想是对一群粒子寻找最优解并使每个粒子都处于最优解状态,能处理连续或离散空间内的数据优化问题。本文根据模糊控制易于解决迟滞、非线性系统问题的特点,将模糊控制与传统PID(Proportion Integral Differential)控制相结合,快速消摆。由于模糊PID控制器参数较多、难以快速调节,采用PSO算法进行优化调整。通过建立起重机防摇数学模型并进行Simulink仿真,对基于粒子群算法的模糊PID控制效果进行分析,为后期桥式起重机防摇控制提供新的理论方法。
1 起重机数学模型
结合桥式起重机的工作过程,将滑轨和货物等抽象为“小车-吊重模型”。小车m受到的驱动力为F,图1为桥式起重机力学结构模型,以从左到右为x轴正向,以垂直地面向下为z轴正向,建立基于右手定则的平面直角坐标系。小车在x轴上滑动,带动吊重m移动,m自由摆动,摆角为θ,假设起重机吊绳为柔性绳,长度为l,不计其质量。在实际滑动过程中,小车与滑轨之间的摩擦阻力f近似与小车速度˙x成线性关系,若摩擦因数为μ,则f=μ˙x。

图1 桥式起重机力学结构模型
基于以上假设,采用拉格朗日方程可得到起重机防摇控制系统的动力学方程为

整理得

2 模糊PID控制器设计
PID控制器的计算公式为

式(3)中:e(t)=r(t)-c(t),e(t)为系统误差,r(t)为系统输入值,c(t)为系统输出值;K、K和K分别为比例、积分和微分系数。
在起重机防摇控制系统中,为使吊重快速并平稳地消摆,将模糊PID控制器设计为两输入(摆角误差e和误差变化率c)-三输出(K、K和K)的控制结构。设e、c、K、K和K的模糊子集为{NB,NM,NS,ZE,PS,PM,PB},分别对应{负大,负中,负小,零,正小,正中,正大}。控制器选择合理的比例因子K和K,在正负边界处分别采用平滑连续的Z型隶属度函数和S型隶属度函数,对中间部分采用灵敏度较强的三角形隶属度函数,在PID算法的基础上对PID控制参数进行模糊自整定,模糊PID控制器的实际控制参数K′、K′和K′的表达式为

式(4)中:K、K和K为模糊PID控制初始值;k、k和k为常量。
根据K、K和K对输出特性的影响,可通过不同的e和c建立模糊规则:当e较大时,K取大提高响应速度,K取小减少超调,K取小或零增强系统的抗干扰能力;当e和c中等大小时,为提高系统的响应速度及减小超调量,K适当取小,K和K取值适中;当e较小时,K和K取大,避免系统振荡;当c较大时,K取小;当c较小时,K取大。模糊控制规则表见表1。

表1 模糊控制规则表
根据表1所示的规则,采用极大-极小法进行推理,采用加权平均数法进行解模糊化,表达式为

式(5)中:μ(x)为输出模糊论域x对应的隶属度函数。
PID初始参数和比例因子决定模糊控制器的性能,但参数的选取主要根据专家知识和试凑法,具有很强的主观性和不确定性。为适配出最优的参数,使控制性能达到最优,需对参数进行寻优处理。
3 PSO算法
PSO算法是由一组粒子在搜索空间中运动,受自身的最佳过去位置pbest和整个群体或近邻的最佳过去位置gbest的影响调整自身位置,最终求得最优解,即每个粒子找到自身的最优解,带动群体粒子找到最优解。PSO算法流程图见图2。每次迭代粒子i的第d维速度的更新公式为

图2 PSO流程图

粒子i的第d维位置的更新公式为

式(6)和(7)中:v为粒子速度;x为粒子位置;w为惯性权值,r和r为加速度因子,在[0,1]中随机产生;c和c为学习因子,一般取2。
先采用算法不断对量化因子K、K和模糊PID控制参数k、k、k进行寻优处理,使模糊PID控制器的控制输出性能最优,达到快速消摆的效果。基于PSO算法优化的模糊PID控制器原理图见图3。
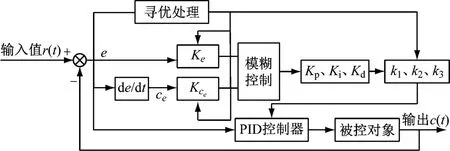
图3 基于PSO算法优化的模糊PID控制器原理图
4 仿真分析
采用PSO算法对桥式起重机防摇控制系统进行Simulink仿真,包括防摇控制系统的Simulink模型和PSO优化算法程序2部分。桥式起重机防摇控制仿真框图见图4。仿真参数为:m=1 000 kg;m=2 000 kg;绳长l=3 m;重力加速度g=9.797 m/s;摩擦因数μ=0.165;在小车静止状态下施加的驱动力F=1 500 N。PSO算法设置的参数:粒子数为100;迭代次数为100;惯性权重ω为0.6;粒子的初始速度、初始位置和加速度因子r和r由随机函数产生;粒子运行的最大速度和最小速度分别设为1和-1;K、K、K、K和K的取值范围均设为[0,300]。
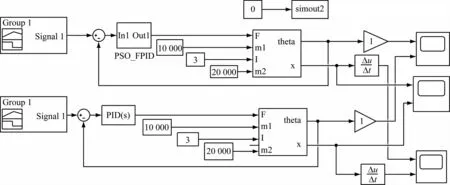
图4 桥式起重机防摇控制仿真框图
模拟起重机实际运载过程,对小车施加驱动F=1 500 N,先施加驱动力0~3 s,不施加驱动力运行一段时间之后,在9~12 s施加一个与该作用力大小相同、方向相反的作用力使小车停下,记录吊重摆动和小车速度曲线,见图5。图5中吊重摆角的绝对值与小车速度的变化率近似呈线性关系。将F作为输入量,将摆角θ作为输出量,分别采用粒子群模糊PID控制算法和传统的PID控制算法进行仿真,关注消摆时间和最大摆角幅度等性能指标的表现。

图5 1 500 N驱动力下起重机仿真曲线图
图6为初始摆角为6°时的摆角消除响应曲线。由图6可知,当初始摆角为6°时,PSO模糊PID控制器的吊重达到稳定状态仅需4.8 s,采用传统PID控制器时吊重需11 s才能到达稳定状态。采用PSO算法优化后的K、K和K分别为22.4、0.2和26.8,将其代入模糊PID控制器中,得到的摆角曲线见图7:当施加的驱动力为1 500 N时,仅采用PID控制,吊重摆角的最大摆幅达到6.42°,停摆时间为28.7 s;采用模糊PID控制器并利用PSO算法优化后的系统停摆时间为15.2 s,最大摆幅仅有1.83°。由此可见,采用PSO算法优化模糊PID参数之后,系统具有良好的稳定性。

图6 初始摆角为6°时的摆角消除响应曲线

图7 不同控制算法的摆角消除响应曲线
5 结 语
对桥式起重机进行防摇控制,既能提高其运输效率,又能延长其使用寿命。本文针对桥式起重机的运载情况建立桥式起重机系统防摇模型,提出了一种基于PSO算法的模糊PID防摇控制系统。通过开展Simulink仿真试验,发现采用基于PSO算法的模糊PID防摇控制效果良好。与传统的PID防摇控制方法相比,该方法在缩短消摆时间和减小摆角幅度方面的表现有明显提升。仿真结果表明,该方法可运用到起重机的防摇控制系统设计中,取代人工操作,实现起重机自动化运输。

