具有非常数死亡率的捕食者-食饵模型的稳定性

董雨欣

（安庆师范大学 数理学院，安徽 安庆 246133）

近年来，捕食者和食饵之间的动力学行为得到了广泛研究，研究人员建立了各种捕食者-食饵模型来研究捕食者和食饵之间丰富的动力学行为[1-2]。如果依赖密度，捕食者必须以某种方式反映食饵数量的变化[3-4]。随着食饵密度的增加，每个捕食者会捕食更多的个体，食饵的密度会迅速固定，Solomon称这种行为为功能反应[5]。在许多经典的捕食者-食饵模型中，捕食者的死亡率经常被考虑在内[6-7]。大多数人认为捕食者的死亡率是一个常数[8]，但是从生态意义上来说，考虑捕食者的非常数死亡率更合理。Duque认为，在没有食饵的情况下，捕食者的死亡率如下[9]：

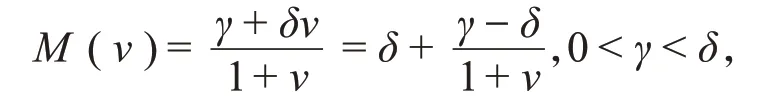
其中，γ是捕食者在低密度下的死亡率，δ是捕食者的最大死亡率，假设γ＜δ。由，

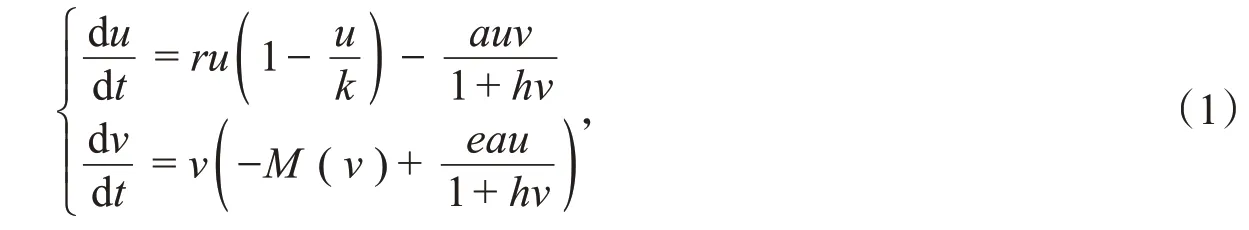
其中，u表示食饵的种群密度，v表示捕食者的种群密度，a表示半饱和常数，h表示捕食者之间的相互干扰，r和k分别表示食饵的内增长率和承载能力，e表示捕食效率，所有参数都是正的。令，去掉横杠得到

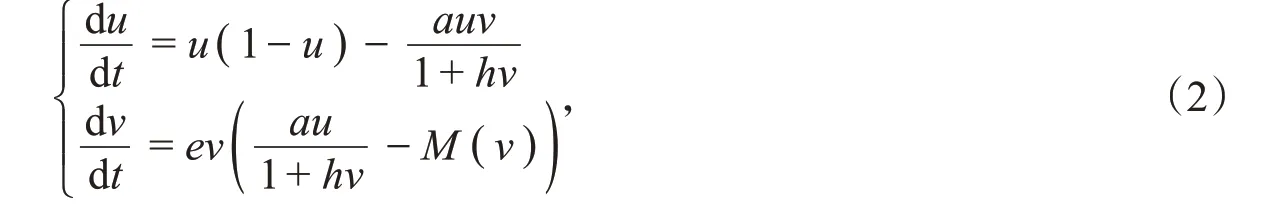
其中，M(v)=。

1 解的正性和有界性

这部分重点讨论系统（2）的解的正性和有界性，就模型的有效性而言，这些讨论非常重要。

定理1对于所有t＞0，系统（2）在初始值(u0,v0)∈下的所有解(u(t),v(t))都是正的。

证明对于任何u≥0和v≥0，有

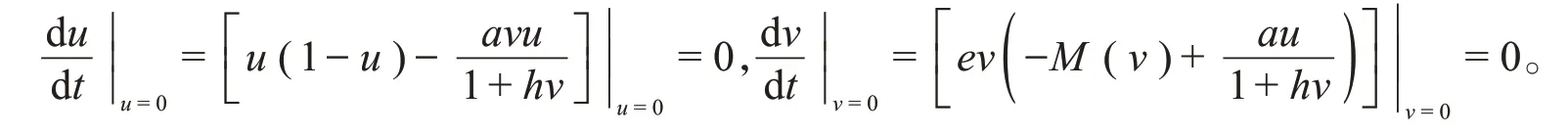
根据解的唯一性，集合对于系统（2）是正不变的，因此，系统（2）的所有解都是正的。

2 正平衡点的存在性

这一部分主要讨论系统（2）的正平衡点的个数。灭绝平衡点和边界平衡点总是存在的，为了分析系统（2）的正平衡点数目，考虑代数方程

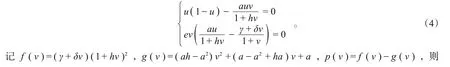
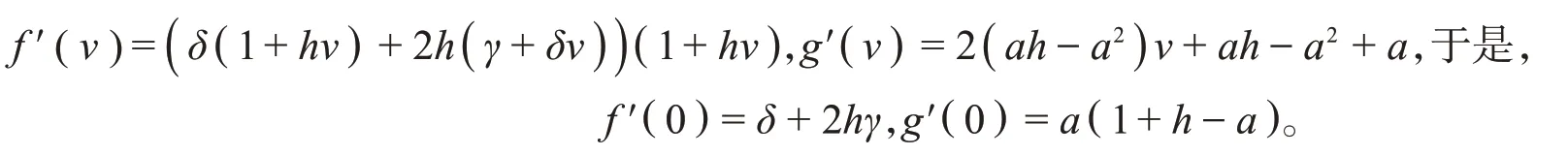
对f(v)，g(v)求二阶导数可得f″(v)=(δh+2hδ)( 1+hv)+(δ( 1+hv)+2h(γ+δv))h，g″(v)=2a(h-a)，于是，f″(0)=4δh+2h2γ，g″(0)=2a(h-a)。

（1）当g′(0)＞f′(0)时，g′(v)与f′(v)有一个交点，记为v1；

（2）当g″(0)＞f″(0)，则p′(v)有一个零点，记为v2；

（3）当g″(0)＞f″(0)，则p″(v)=0有一个正根，记为v3。

为更清楚地说明方程（2）的正根个数，将条件和相应正根的个数分别列于表1。

表1 方程（2）的正根个数

根据上面的讨论可得到如下关于正平衡点的结论。

定理3当g′(0)≥f′(0)时，系统（2）最多存在2个正平衡点；当g′(0)＜f′(0)时，系统（2）最多存在3个正平衡点。

3 平衡点的稳定性分析

经过计算，可以发现方程（4）最多有3个正根，说明系统（2）的动力学行为更加丰富。对于任何参数，系统（2）中的边界平衡点E2(K,0)和灭绝平衡点E0(0,0)一定存在。下面只讨论系统（2）有一个内部平衡点的情况。

平衡点的稳定性由雅可比矩阵的特征值决定，系统（2）的雅可比矩阵是

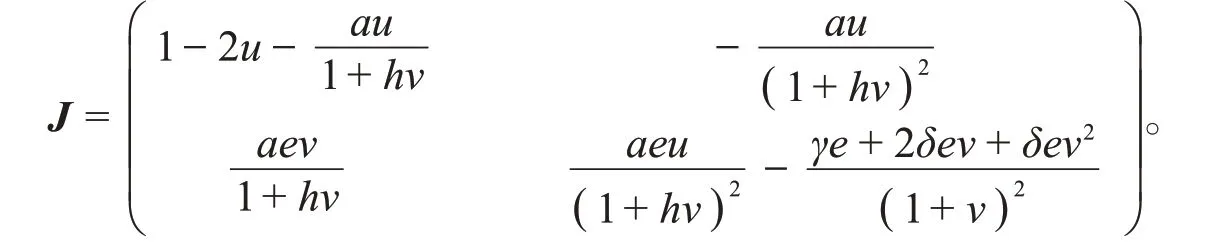
在灭绝平衡点E0( 0,0)处的特征值为γ和-b，因此E0( 0,0)是一个鞍点。E2( 1,0)表示没有捕食者的边界平衡点。

定理4当a＜γ时，边界平衡点E2( 1,0)是稳定的；当a＞γ时，边界平衡点E2( 1,0)是不稳定的。

证明平衡点E2( 1,0)处Jacobian矩阵的行列式和迹分别为

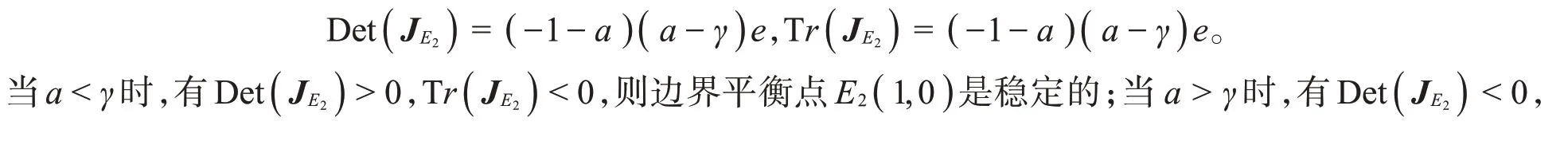
4 数值模拟

这部分借助Matlab数值模拟来验证边界平衡点的稳定性、内部平衡点的存在性及稳定性。

4.1 边界平衡点的稳定性

在定理4的a＜γ条件下，选取一组参数h=0.1，γ=0.2，δ=0.5，a=0.1，e=2，得边界平衡点E2( 1,0)对应的相图轨线，如图1（a）所示。由图1（a）可以看出，边界平衡点E2( 1,0)是稳定的，与定理4的结论一致。在定理4 的a＞γ条件下，选取一组参数h=0.1，γ=0.2，δ=0.5，a=0.5，e=2，那么边界平衡点E2( 1,0)对应的相图轨线如图1（b）所示。由图1（b）可以看出，边界平衡点E2( 1,0)是不稳定的，与定理4的结论也一致。

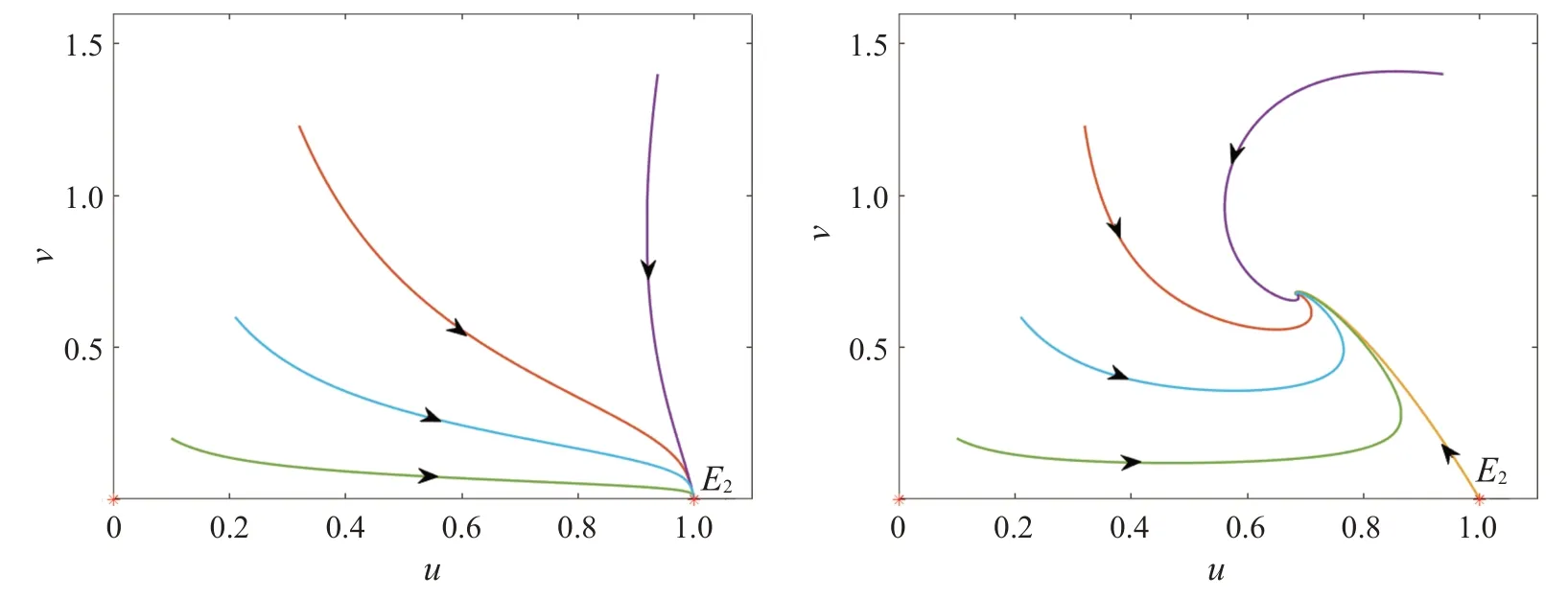
图1 （a）a ＜γ，（b）a ＞γ时，边界平衡点E2( 1,0)对应的相图轨线

4.2 内部平衡点的存在性和稳定性

系统（2）在定理3的g′(0)＞f′(0)条件下，选取一组参数h=1，γ=0.22，δ=0.25，a=0.4，e=2，记系统（2）的上下方程是y和g，系统（2）在这组参数下的图像如图2所示。可以清楚地看到，第一象限内系统（2）在这组参数下只有一个内部平衡点，借助Matlab计算可知，内部平衡点的值是（0.865 7，0.505 1）。内部平衡点记为E1(u1,v1)，计算可得Tr()=-1.127 9 ＜0 和Det()=0.202 3 ＞0，E1的轨线相图如图3所示。从图3可以看出平衡点E1(u1,v1)是稳定结点，这和定理5的结论一致。

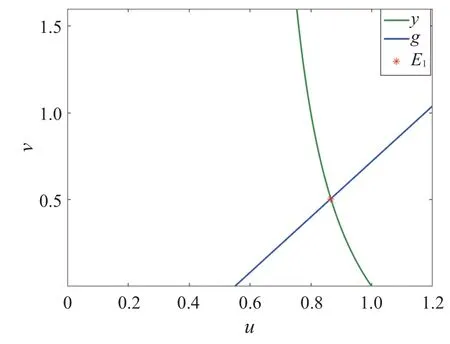
图2 系统（2）在第一象限内的平衡点

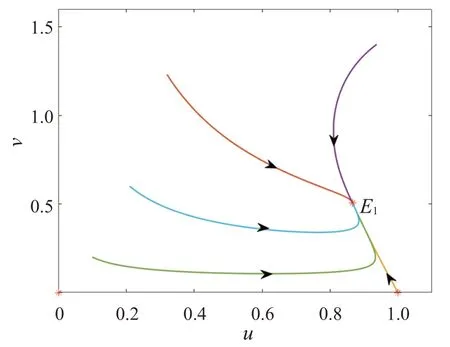
图3 E1的轨线相图

5 结束语

综上所述，本文研究了一类具有非常数死亡率的捕食者-食饵模型，与含有常数死亡率的捕食者-食饵模型相比，平衡点个数增加，出现了3个共存平衡点，使模型的生物意义增强。从生物学的角度看，捕食者的死亡率通常不是一个常数，因此，考虑捕食者的非常数死亡率比常数死亡率更合理。在生态学中，研究捕食者的非常数死亡率是一个非常基本且重要的问题，它对捕食者-食饵模型有着很大的影响，且使捕食者-食饵模型的动力学行为更加丰富。